Ensuring the Reliability of Your Model Checker: Interval Iteration for Markov Decision Processes

Abstract

Probabilistic model checking provides formal guarantees on quantitative properties such as reliability, performance or risk, so the accuracy of the numerical results that it returns is critical. However, recent results have shown that implementations of value iteration, a widely used iterative numerical method for computing reachability probabilities, can return results that are incorrect by several orders of magnitude. To remedy this, interval iteration, which instead converges simultaneously from both above and below, has been proposed. In this paper, we present interval iteration techniques for computing expected accumulated weights (or costs), a considerably broader class of properties. This relies on an efficient, mainly graph-based method to determine lower and upper bounds for extremal expected accumulated weights. To offset the additional effort of dual convergence, we also propose topological interval iteration, which increases efficiency using a model decomposition into strongly connected components. Finally, we present a detailed experimental evaluation, which highlights inaccuracies in standard benchmarks, rather than just artificial examples, and illustrates the feasibility of our techniques.

The authors at Technische Universität Dresden are supported by the DFG through the Collaborative Research Center SFB 912 – HAEC, the Excellence Initiative by the German Federal and State Governments (cluster of excellence cfaed), the Research Training Groups QuantLA (GRK 1763) and RoSI (GRK 1907) and the DFG-project BA-1679/11-1. David Parker is part-funded by the PRINCESS project, under the DARPA BRASS programme.

1 Introduction

Over the past twenty years, many algorithms, logics and tools have been developed for the formal analysis of probabilistic systems. They combine techniques developed by the model-checking community with methods for the analysis of stochastic models (see, e.g., [1, 8, 20]). A widely used model is Markov decision processes (MDPs), which represent probabilistic systems with nondeterminism, needed to model, for example, concurrency, adversarial behaviour or control.

Various model checking problems on MDPs are reducible to the task of computing extremal (maximal or minimal) probabilities of reaching a goal state, ranging over all schedulers [2, 4, 12, 15]. Schedulers, also often called policies, adversaries or strategies, represent the possible ways of resolving nondeterminism in an MDP. So extremal probabilities correspond to a worst-case or best-case analysis, for example, the maximal or minimal probability of a system failure.

Weighted MDPs, i.e., MDPs where rational weights are attached to the state-action pairs, provide a versatile modelling formalism that allows reasoning about, e.g., extremal values for the expected accumulation of weights until reaching a goal state. These might represent worst-case or best-case scenarios for expected costs (e.g., execution time, energy usage) or utility values. To compute schedulers that maximize or minimize the expected accumulated weight, one can rely on techniques that are known for stochastic shortest path problems [7, 16].

The computation of extremal values for reachability probabilities or expected accumulated weights until reaching a goal can be done using linear programming techniques or iterative computation schemes. In the context of probabilistic model checking, the latter are more common since they typically scale to the analysis of larger systems. Common techniques for this are value iteration [6], policy iteration [21] or mixtures thereof [29]. We focus here on value iteration which relies on a fixed-point characterization $e^*=f(e^*)$ of the extremal probability or expectation vector $e^*$ based on the Bellman equation [6] and computes an approximation thereof by successive application of the fixed-point operator f.

In practice, a stopping criterion is required to determine when this iterative approximation process can be safely terminated. For discounted variants of expected accumulated weights, convergence is guaranteed and the discount factor can be used to derive a safe stopping criterion ensuring that the computed vector $f^n(z)$ is indeed an $\varepsilon$-approximation of the desired discounted expectation vector $e^*$ for a given tolerance $\varepsilon >0$. (Here, z stands for the starting vector.) For the purposes of model checking, however, non-discounted variants are usually preferred, in order to compute meaningful values for properties such as execution time or energy usage, or indeed reachability probabilities, where discounting makes little sense. For the non-discounted case, with some appropriate preprocessing and model assumptions, convergence of value iteration can still be guaranteed as the fixed-point operator f can shown to be contracting [7, 16], but sound stopping criteria are more difficult.

To check termination of value iteration, most practical implementations simply terminate when the last two vectors $f^{n-1}(z)$ and $f^n(z)$ differ by at most $\varepsilon$ with respect to the supremum norm. This prevalent stopping criterion is currently realized in widely used probabilistic model checkers such as PRISM [25], MRMC [23] and IscasMC [19], as well as in other implementations such as the MDP Toolbox [10]. However, recent results from Haddad and Monmege [18] have shown that the results obtained from value iteration for reachability probabilities with this naive stopping criterion can be extremely inaccurate. On our tests using a simple example from [18], all three of the above model checkers fail. On a small MDP with 41 states (see [3] for details), MRMC returns 0 and PRISM returns $\sim$0.1943 where the correct result should be 0.5.

So, [18] proposes a refinement of value iteration for computing maximal or minimal reachability probabilities, called interval iteration. After some graph-based preprocessing to ensure convergence, it relies on the monotonicity of the fixed-point operator f and carries out the iterative application of f to two starting vectors x and y such that $f^n(x) \leqslant e^* \leqslant f^n(y)$ for all n. Here, x is a lower bound for the required probability vector $e^*$ and y is an upper bound. Thus, if all entries of the vector $f^n(y)-f^n(x)$ are smaller than $\varepsilon$, then both $f^n(x)$ and $f^n(y)$ are sound $\varepsilon$-approximations of z. [18] does not report on experimental studies or weights. So, it leaves open whether interval iteration is feasible in practice and yields a reasonable way to ensure the reliability of the model-checking results.

Contribution. Inspired by the work of Haddad and Monmege [18], we present an interval-iteration approach for computing maximal expected accumulated (non-discounted) weights in finite-state MDPs with a distinguished goal state $final$.¹ The weights can be negative or positive numbers. To ensure the existence of a deterministic memoryless scheduler maximizing the expected accumulated weights until reaching $final$, we assume that the MDP is contracting in the sense that the goal state will almost surely be reached, no matter which scheduler or which starting state is selected.² While the null vector $x=0$ and the vector $y=1$ where all components have value 1 obviously yield correct lower resp. upper bounds for any probability vector, the main problem for adapting the interval-iteration approach to maximal or minimal expected accumulated weights is to provide efficient algorithms for the computation of lower and upper bounds. We provide here two variants to compute lower and upper bounds that are based on bounds for the recurrence times of states under memoryless schedulers.

After presenting the foundations of the interval-iteration approach for expected accumulated weights (Sect. 3), we propose topological interval iteration, which embeds the basic algorithm into a stratified approach that speeds up the computation time by treating the strongly connected components separately (Sect. 4). Sections 5 and 6 will report on experimental results carried out with an implementation of the interval-iteration approaches of [18] for reachability probabilities and our approach for maximal or minimal expectations applied to MDPs with non-negative weights. Proofs omitted in this paper, as well as further details on our experiments, can be found in the appendix of the extended version [3], which is available together with our implementation at http://wwwtcs.inf.tu-dresden.de/ALGI/PUB/CAV17/.

Related Work. Bell and Haverkort [5] reported on serious problems with the precision of the implementations for computing steady-state probabilities in continuous-time Markov chains. Wimmer et al. [31] revealed several problems with the implementations of model checking algorithms for Markov chains and properties of probabilistic computation tree logic (PCTL). They identified several sources of imprecise results, including numerical problems with floating-point arithmetic and issues that are specific to symbolic BDD-based implementations, and presented ideas for how such problems can be avoided.

Although [31] also identifies the widely used termination criterion for iterative computation schemes as a potential source of inaccuracy, they do not provide a solution for it. To the best of our knowledge, the paper by Haddad and Monmege [18] is the first one which addresses the termination problem of iterative computation schemes for MDPs. However, [18] only considers extremal probabilities and does not report on experimental studies. Prior to this, Brázdil et al. [9] presented an extension of bounded real-time dynamic programming [27], which also yields interval bounds for extremal probabilities in MDPs. The techniques were extended to handle arbitrary MDPs and full LTL model checking, but again focused on probabilities, not weights. We are not aware of any efficiently realizable safe termination conditions of value iteration proposed for expected (non-discounted) accumulated weights. The technique proposed here follows the interval-iteration approach of [18]. While – after some appropriate preprocessing – [18] can deal with 0 and 1 as lower resp. upper bound for the desired minimal or maximal probabilities, efficient computation schemes for lower and upper bounds for minimal or maximal expected accumulated weights are not obvious.

In fact, such bounds can also be interesting for different purposes. In the context of planning, [27] presents an efficient algorithm to compute an upper bound for the minimal expected accumulated weight until reaching a goal, which they call Dijkstra Sweep for Monotone Pessimistic Initialization (DS-MPI). This approach (which we consider in the experiments in Sect. 6) is designed for MDPs where all weights are non-negative. As it relies on the idea to generate a memoryless scheduler and an upper bound for its expected accumulated weight, there is no straightforward adaption of the approach of [27] to compute an upper bound for the maximal expected accumulated weight.

Lastly, computation of exact extremal reachability probabilities in MDPs was also considered by Giro [17], where, by exploiting the special structure of the linear programs that need to be solved for reachability probabilities, the use of simplex or other generic exact linear program solvers is avoided.

2 Preliminaries

Throughout the paper, we assume some familiarity with basic concepts of Markov decision processes (MDPs), see, e.g., [22, 30]. We briefly explain our notations.

A plain MDP is a tuple $\mathcal {M}= (S, Act ,P)$ where S is a finite state space, $Act$ a finite set of actions, and $P: S \times Act \times S \rightarrow \mathbb {Q}\cap [0,1]$ a function such that $\sum _{t\in S} P(s,\alpha ,t)\in \{0,1\}$ for all state-action pairs $(s,\alpha )\in S \times Act$. If $s\in S$, $\alpha \in Act$ and $T \subseteq S$ then $P(s,\alpha ,T) = \sum _{t\in T} P(s,\alpha ,t)$. We write $Act (s)$ for the set of actions $\alpha \in Act$ such that $\sum _{t\in S} P(s,\alpha ,t)=1$. State s is called a trap state if $Act (s)$ is empty. A path in $\mathcal {M}$ is a sequence $\pi = s_0 \, \alpha _0 \, s_1 \, \alpha _1 \, s_2 \, \alpha _2 \ldots$ that alternates between states and actions such that $\alpha _i \in Act (s_i)$ and $P(s_i,\alpha _i,s_{i+1})>0$ for all i and such that $\pi$ is either finite and ends in a state or infinite. $\pi$ is called maximal if $\pi$ is either infinite or finite and $\pi$’s last state is a trap state. A (deterministic) scheduler $\mathfrak {S}$ for $\mathcal {M}$, also called policy or adversary, is a function that assigns to each finite path $\pi$ ending in a non-trap state s an action in $Act (s)$. $\mathfrak {S}$ is called memoryless if $\mathfrak {S}(\pi )=\mathfrak {S}(\pi ')$ whenever $\pi$ and $\pi '$ end in the same state. We write $\mathrm {Pr}^{\mathfrak {S}}_{\mathcal {M},s}$, or simply $\mathrm {Pr}^{\mathfrak {S}}_{s}$, to denote the standard probability measure on maximal paths induced by $\mathfrak {S}$, starting from state s. The notations $\mathrm {Pr}^{\max }_s(\varphi )$ and $\mathrm {Pr}^{\min }_s(\varphi )$ will be used for the extremal probabilities for the event $\varphi$ when ranging over all schedulers. We often will use the LTL-like temporal modalities $\Diamond$ (eventually), $\Box$ (always), $\bigcirc$ (next) and ${{\mathrm{{{\mathrm{\mathrm {U}}}}}}}$ (until) to specify measurable sets of maximal paths.

A weighted MDP, briefly called MDP, is a tuple $\mathcal {M}=(S, Act ,P, final , wgt )$ where $(S, Act ,P)$ is a plain MDP as above, $final \in S$ a distinguished trap state and $wgt : S \times Act \rightarrow \mathbb {Q}$ is a weight function that might have positive and negative values. Throughout the paper, we suppose that $\mathcal {M}$ is contracting in the sense that $\mathrm {Pr}^{\mathfrak {S}}_{s}(\Diamond final )=1$ for all states $s\in S$. Given a finite path $\pi = s_0 \, \alpha _0 \, s_1 \, \alpha _1 \, \ldots \, \alpha _{n-1} \, s_n$, the accumulated weight of $\pi$ is $wgt (\pi )= wgt (s_0,\alpha _0)+ wgt (s_1,\alpha _1)+\ldots + wgt (s_{n-1},\alpha _{n-1})$. We write to denote the function that assigns to each finite path ending in $final$ its accumulated weight. Given a scheduler $\mathfrak {S}$ for $\mathcal {M}$, let denote the expectation of under $\mathfrak {S}$ for starting state s. We consider the value iteration for computing $\varepsilon$-approximations for , or briefly , which is defined as where $\mathfrak {S}$ ranges over all schedulers. As $\mathcal {M}$ is supposed to be contracting, is the expected total weight from s under $\mathfrak {S}$ and there is a deterministic memoryless scheduler $\mathfrak {S}$ with [7, 22].

3 Interval Iteration for Weighted MDPs

Throughout the paper, $\mathcal {M}=(S, Act ,P, final , wgt )$ is a weighted MDP as in Sect. 2 satisfying $\mathrm {Pr}^{\mathfrak {S}}_{s}(\Diamond final )=1$ for all states $s\in S$ and schedulers $\mathfrak {S}$, i.e., that the MDP is contracting. We start in Sect. 3.1 with a brief summary of known fixed-point characterizations of the vector with maximal expected accumulated weights that yield the foundations for the standard value iteration. Sections 3.2 and 3.3 then present the details of the interval iteration and efficient computation schemes for lower and upper bounds for the maximal expected accumulated weights.

3.1 Value Iteration in Weighted MDPs

In what follows, we briefly recall known (and some simple) facts about the foundations of the value iteration to compute maximal expected total weights in MDPs. Let $f : \mathbb {R}^{|S|} \rightarrow \mathbb {R}^{|S|}$ denote the following function. Given a vector $z = (z_s)_{s\in S}$ in $\mathbb {R}^{|S|}$ then $f(z)=(f_s(z))_{s\in S}$ where $f_{ final }(z)=0$ and

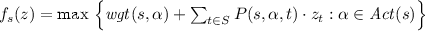
for all states $s \in S \setminus \{ final \}$. The functions $f^n : \mathbb {R}^{|S|} \rightarrow \mathbb {R}^{|S|}$ are defined inductively by $f^0=\mathrm {id}$, $f^1=f$ and $f^{n+1}= f \circ f^n$ for $n \in \mathbb {N}$, $n\geqslant 1$. Let $e^* = (e^*_s)_{s\in S}$ denote the vector with the maximal expected total weights for all states, i.e., . For $z=(z_s)_{s\in S} \in \mathbb {R}^{|S|}$ and $z'=(z'_s)_{s\in S} \in \mathbb {R}^{|S|}$ we then write $z \leqslant z'$ if $z_s\leqslant z'_s$ for all $s\in S$. Furthermore, $\Vert \cdot \Vert$ denotes the supremum norm for vectors in $\mathbb {R}^{S}$. That is, $\Vert z\Vert = \max _{s\in S} |z_s|$.

The series $(f^n(z))_{n\in \mathbb {N}}$ converges to its unique fixed point $e^*$ monotonically increasing if $z \leqslant e^* \wedge z \leqslant f(z)$ and decreasing if $z \geqslant e^* \wedge z \geqslant f(z)$ (see [3]). This provides the basis for linear programming approaches to compute the exact values $e^*_s$ and for the value iteration that successively generates the vectors $z, f(z), f^2(z) f^3(z), \ldots$ and finally returns one of the vectors $f^n(z)$ as an approximation of $e^*$. However, there are two problems:

• (P1) How to find a starting vector z with $z \leqslant e^* \wedge z \leqslant f(z)$ or $z \geqslant e^* \wedge z \geqslant f(z)$?

• (P2) How to check whether $\Vert f^n(z) - e^* \Vert < \varepsilon$, given a tolerance $\varepsilon > 0$, a starting vector z from (P1) and the first $n{+}1$ vectors $z,f(z),\ldots ,f^n(z)$ of the value iteration?

Problem (P1). Problem (P1) is specific to the case of maximal or minimal expectations, as (after some preprocessing to ensure the uniqueness of the fixed point) the corresponding fixed-point operator f for reachability probabilities guarantees that $0 \leqslant z \leqslant 1$ implies $0 \leqslant f(z) \leqslant 1$. For certain models with syntactic restrictions, problem (P1) can be answered directly as the null vector $z=0$ is known to satisfy the conditions $z \leqslant e^* \wedge z \leqslant f(z)$ or $z \geqslant e^* \wedge z \geqslant f(z)$ for monotonic convergence. Prominent examples are positive bounded MDPs where each state s has an action $\alpha$ with $wgt (s,\alpha ) \geqslant 0$, or MDPs where all weights are non-positive. In both cases, monotonic convergence of $(f^n(0))_{n \in \mathbb {N}}$ can be guaranteed even for countable state spaces (see [30]). However, for MDPs with negative and positive weights, it might be hard to find starting vectors z that ensure monotone convergence, which requires to determine lower and upper bounds for the maximal expected accumulated weight. To the best of our knowledge, even for finite-state positive bounded MDPs, techniques to determine an upper bound have not been addressed in the literature. Besides the algorithm for lower bounds for MDPs with non-positive weights proposed in [27], we are not aware of any technique proposed in the literature to find an appropriate starting vector for the lower value iteration in weighted MDPs.

Fig. 1.

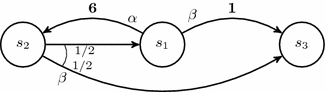
Markov decision process of Example 3.1. Only non-zero probabilities and weights (in bold) are shown.

Example 3.1

To illustrate that there might be vectors z that do not lead to monotonic convergence, e.g., with $z_s< e_s^* < f_s(z)$ or $e_s^*< z_s < f_s(z)$, even when all weights are non-negative, consider the MDP $\mathcal {M}$ in Fig. 1 with three states $s_1, s_2$ and $s_3= final$ and $P(s_1,\alpha ,s_2)= P(s_1,\beta ,s_3)= 1$, $P(s_2,\beta ,s_1)= P(s_2,\beta ,s_3)= 1/2$, $wgt (s_1,\alpha ) = 6$, $wgt (s_1,\beta )=1$, while $P(\cdot )=0$ and $wgt (\cdot )=0$ in all remaining cases. Then, $e^* = (12,6,0)$. For the starting vector $z=(0,9,0)$ we have $f(z) = (15,0,0)$, in which case $z_s =0< e_s^* =12 < f_s(z)=15$ for $s=s_1$. Monotonic convergence can not even be guaranteed if the starting vector z satisfies $z \leqslant e^*$ or $z \geqslant e^*$ as, for instance, $z= (14,10,0) \geqslant (12,6,0)=e^*$ but $f(z)= (16,7,0)$, i.e., $e_s^*=12< z_s=14 < f_s(z) =16$ for $s=s_1$.    $\blacksquare$

Problem (P2). Many implementations of the value iteration terminate as soon as $\Vert f^{n}(z) - f^{n-1}(z)\Vert < \varepsilon$ for some user-defined tolerance $\varepsilon > 0$ and return the vector $f^{n}(z)$. The problem is that $f^n(z)$ need not be an $\varepsilon$-approximation of the vector $e^*$. This phenomenon has been first observed in [18] for value iteration to compute (maximal or minimal) reachability probabilities in Markov chains or MDPs. The following example is an adaption of an example provided in [18] for reachability probabilities to the case of expected total weights and illustrates the problem of premature termination potentially leading to serious imprecision.

Fig. 2.

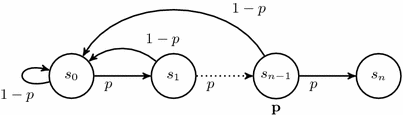
Markov chain of Example 3.2. Only non-zero probabilities and weights (in bold) are shown.

Example 3.2

Let $p \in \mathbb {Q}$ with $0< p < 1$ and let $\mathcal {C}[p]$ be the Markov chain in Fig. 2 with state space $S = \{s_0,s_1,\ldots ,s_{n-1},s_n\}$ where $s_n= final$, transition probabilities $P(s_i,s_{i+1}) = p$, $P(s_i,s_0) = 1 - p$ and weights $wgt (s_{n-1}) = p$ for $0 \leqslant i < n$ and $P(\cdot )= wgt (\cdot )=0$ in all other cases.³ Then, $\mathrm {Pr}_{s}(\Diamond final )=1$ and expected total weight $e^*_{s}=1$ for $s \not = final$. Now consider $p=1/2$ and the tolerance $\varepsilon = 1/2^{n}$. The value iteration finds $0< f_s^n(0) - f^{n-1}_s(0) = 1/2^{n+1} < \varepsilon$ and therefore returns the vector $f^n(0)$, even though the difference between $f^n(0)$ and the correct result $e^*_{s}$ is significantly larger than $\varepsilon$, i.e., $e^*_{s} - f_{s}^{n}(0) = 1 - (1/2^{n+1} + 1/2^{n-i}) \geqslant 3/8 > \varepsilon$. (See [3].)    $\blacksquare$

3.2 Lower and Upper Value Iteration

Following the ideas of [18], we present an approach with two value iterations that generate sequences of vectors in $\mathbb {Q}^{|S|}$: one that converges to the vector $e^*$ from below (called lower value iteration) and one that converges to $e^*$ from above (called upper value iteration). As soon as the vectors of the lower and the upper value iteration differ by components by at most $\varepsilon$ then $\varepsilon$-approximations of the values $e^*_s$ have been generated. In this way, we avoid problem (P2).

Both the lower and the upper value iteration rely on a preprocessing to determine starting vectors $x = (x_s)_{s\in S}$ and $y = (y_s)_{s\in S}$ with

We then have $f^n(x) \leqslant e^* \leqslant f^n(y)$ for all $n\in \mathbb {N}$ and both sequences $(f^n(x))_{n\in \mathbb {N}}$ and $(f^n(y))_{n\in \mathbb {N}}$ converge to $e^*$ (see [3]). Monotonicity does not hold in general as $f^{n}_s(x)< f^{n-1}_s(x) < e_s^*$ or $e^*_s< f^{n-1}_s(y) < f^{n}_s(y)$ is possible (see Example 3.1). However, with a slightly modified approach of the value iteration (see below) the assumption $x \leqslant f(x)$ or $y \leqslant f(y)$ is irrelevant. This simplifies problem (P1). The computation of starting vectors x and y satisfying (${}^{*}$) will be addressed in Sect. 3.3.

Modified Value Iteration. We suggest a mild variant of the standard value iteration where monotonicity is ensured by construction. Suppose we are given vectors x and y satisfying (${}^{*}$). We define inductively vectors $x^{(n)} = (x_s^{n})_{s\in S}$ and $y^{(n)} = (y_s^{n})_{s\in S}$ by $x^{(0)} = x$, $y^{(0)} = y$ and for all $n\in \mathbb {N}$ and $s \in S \setminus \{ final \}$:

$$\begin{aligned} x_s^{(n+1)}= \max \ \left\{ x_s^{(n)}, \ f_s\bigl (x^{(n)}\bigr )\right\} \qquad y_s^{(n+1)} = \min \ \left\{ y_s^{(n)}, \ f_s\bigl (y^{(n)}\bigr )\right\} \end{aligned}$$

and $x_{ final }^{(n)} = y_{ final }^{(n)}=0$. Lemma 3.3 (see [3] for its proof) states the essential properties of the lower and upper value iteration.

Lemma 3.3

Suppose holds. Then:

• (a) $x^{(n)} \ \leqslant \ e^* \ \leqslant \ y^{(n)}$ for all $n \in \mathbb {N}$

• (b) $x^{(0)} \ \leqslant \ x^{(1)} \ \leqslant \ x^{(2)}\ \leqslant \ \ldots$ and $\lim \limits _{n \rightarrow \infty } x^{(n)} = e^*$

• (c) $y^{(0)} \ \geqslant \ y^{(1)} \ \geqslant \ y^{(2)}\ \geqslant \ \ldots$ and $\lim \limits _{n \rightarrow \infty } y^{(n)} = e^*$

Thanks to monotonicity, we can use a Gauss-Seidel-like iteration variant with forward substitution that relies on an enumeration $s_1,s_2,\ldots ,s_N$ of all states in S. The idea is to iterate values in sequence according to this enumeration. Then, in each step, the already updated values of previous states can be re-used. For this, we inductively define vectors $\tilde{x}^{(n)} = (\tilde{x}_s^{n})_{s\in S}$ and $\tilde{y}^{(n)} = (\tilde{y}_s^{n})_{s\in S}$ by $\tilde{x}^{(0)} = x$, $\tilde{y}^{(0)} = y$ and for all $n\in \mathbb {N}$ and $s \in S \setminus \{ final \}$:

and $\tilde{x}_{ final }^{(n)} = \tilde{y}_{ final }^{(n)}=0$ where $\tilde{x}^{(n,i)} = \bigl (\tilde{x}_s^{(n,i)}\bigr )_{s\in S}$ with $\tilde{x}_{s_j}^{(n,i)}$ being $\tilde{x}_{s_j}^{(n+1)}$ for $j<i - 1$ and $\tilde{x}_{s_j}^{(n)}$ otherwise. The definition of $\tilde{y}^{(n,i)}$ is analogous. Then, by induction and using the monotonicity of f we get the monotone convergence to $e^*$ from below (resp. above) for the sequence $(x^{(n)})_{n\in \mathbb {N}}$ (resp. $(y^{(n)})_{n\in \mathbb {N}}$.

3.3 Computing Starting Vectors

The remaining problem is to find an efficient method for computing starting vectors x and y such that (${}^{*}$) holds. For this, we first use the observation that, for each memoryless deterministic scheduler $\mathfrak {S}$, the expected weight until reaching $final$ can be derived by multiplying the weights by the expected number of visits to each of the states, as $final$ is a trap state and is reached with probability 1:

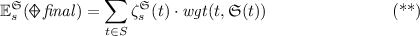
where $\zeta ^{\mathfrak {S}}_s(t)$ denotes the expected number of times to visit t in the Markov chain induced by $\mathfrak {S}$ with starting state s and $wgt (t,\mathfrak {S}(t))$ is the weight for the action that is selected by $\mathfrak {S}$ in state t. Thus, if

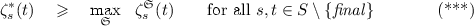
where $\mathfrak {S}$ ranges over all memoryless deterministic schedulers then we may start the lower and upper value iteration with the following vectors $x=(x_s)_{s\in S}$ and $y = (y_s)_{s\in S}$. The components for the trap state are $x_{ final }=y_{ final }=0$. For each state s, let $R_s$ be the set of states reachable from s. We then define:

Here, for $t \in S \setminus \{ final \}$, $wgt ^{\min }(t)= \min W(t)$, $wgt ^{\max }(t)= \max W(t)$ where $W(t)=\{0\}\cup \{ wgt (t,\beta ) : \beta \in Act (t)\}$ and $wgt ^{\min }( final ) = wgt ^{\max }( final ) = 0$. Then, (${}^{*}$) follows from (${}^{**}$) and (${}^{***}$) as $wgt ^{\min }(t)$ is non-positive and

$$ \zeta ^*_s(t)\cdot wgt ^{\min }(t) \leqslant \zeta ^{\mathfrak {S}}_s(t) \cdot wgt (t,\mathfrak {S}(t)) \leqslant \zeta ^*_s(t)\cdot wgt ^{\max }(t) $$

for all states $s,t \in S \setminus \{ final \}$ and all schedulers $\mathfrak {S}$. Moreover, $\zeta _s^{\mathfrak {S}}(t)=0$ if $t \notin R_s$.

Remark 3.4

For the special case of MDPs with non-negative weights, the starting vector x obtained by our approach for the lower value iteration agrees with the classical text-book approach (see, e.g., Sects. 7.2.4 and 7.3.3 in [30]). More precisely, as $wgt \geqslant 0$ implies $wgt ^{\min }=0$, the lower value iteration for approximating the maximal expected total weight will be started with $x^{(0)}=0$. For computing approximations of minimal expected total weights, we switch from $wgt$ to $- wgt$ and then apply the lower and upper value iteration. As $wgt \geqslant 0$ implies $(- wgt )^{\max }=0$ the upper value iteration will be started with the null vector $y^{(0)}=0$, which corresponds to the classical approach.    $\blacksquare$

We now present simple techniques to compute values $\zeta ^*_s(t)$ satisfying (${}^{***}$). If $\mathcal {M}$ is acyclic then $\zeta ^{\mathfrak {S}}_s(t)\leqslant 1$ for all states s, t. Thus, for acyclic MDPs we can deal with $\zeta ^*_s(t)=1$ for all states s, t. In the sequel, we suppose that $\mathcal {M}$ is cyclic.

Lemma 3.5

Let $\mathfrak {S}$ be a memoryless deterministic scheduler. Then, for all states $s,t \in S \setminus \{ final \}$:

$$ \zeta ^{\mathfrak {S}}_s(t) = \frac{\mathrm {Pr}^{\mathfrak {S}}_s(\Diamond t)}{1 - \mathrm {Pr}^{\mathfrak {S}}_t(\bigcirc \Diamond t)} $$

As a consequence of Lemma 3.5 (see [3] for its proof) we get that to ensure (${}^{***}$) we can deal with any value

$$ \zeta _s^*(t) = \frac{\mathrm {Pr}^{\text {ub}}_s(\Diamond t)}{1 - \mathrm {Pr}^{\text {ub}}_t(\bigcirc \Diamond t)} $$

where $\mathrm {Pr}^{\text {ub}}_t(\bigcirc \Diamond t) < 1$ is an upper bound for $\mathrm {Pr}^{\max }_t(\bigcirc \Diamond t)$ and $\mathrm {Pr}^{\text {ub}}_s(\Diamond t)$ an upper bound for $\mathrm {Pr}^{\max }_s(\Diamond t)$. One option to obtain appropriate values $\mathrm {Pr}^{\text {ub}}_t(\bigcirc \Diamond t)$ and $\mathrm {Pr}^{\text {ub}}_s(\Diamond t)$ is to apply the upper value iteration proposed in [18] for an arbitrary number of steps. However, this requires individual computations for each state t, which becomes expensive for larger models.

Then, there is a tradeoff between providing good bounds using sophisticated techniques and the time (and memory) requirements to compute such bounds. In what follows, we present two simple graph-based techniques to compute upper bounds for $\zeta _s^*(t)$. Both rely on the trivial bound 1 for $\mathrm {Pr}^{\max }_s(\Diamond t)$, i.e., $\zeta _s^*(t)$ depends on s only implicitly by the choice of the set $R_s$, and compute an upper bound for the maximal recurrence probabilities $\mathrm {Pr}^{\max }_t(\bigcirc \Diamond t)$.

Upper Bound for Maximal Recurrence Probabilities (Variant 1). For $s\in S$, we write $C_s$ to denote the unique strongly connected component (SCC) of $\mathcal {M}$ that contains s.⁴ For $t\in S \setminus \{ final \}$, let $X_t$ denotes the set of all state-action pairs $(s,\alpha )$ with $s\in C_t$ (hence $C_s=C_t$) and $P(s,\alpha ,C_t) <1$ and let

$$\begin{aligned} q_t&= \max \bigl \{P(s,\alpha ,C_t): (s,\alpha ) \in X_t \bigr \}\\[1ex] p_t&= \min \bigl \{P(s,\alpha ,u): s,u\in C_t, \ \alpha \in Act (s), \ P(s,\alpha ,u)>0 \bigr \} \end{aligned}$$

Note that the assumption $\mathrm {Pr}^{\min }_t(\Diamond final )=1$ for all t ensures that $X_t$ is nonempty. Let $q = \max _t q_t$ and p denote the minimal positive transition probability in $\mathcal {M}$, i.e., $p = \min \{ P(s,\alpha ,t) : s \in S, \alpha \in Act (s), P(s,\alpha ,t)>0 \}$. Then, $0< p \leqslant p_t <1$ and $0< q_t \leqslant q <1$.

Lemma 3.6

Let $\mathfrak {S}$ be a memoryless deterministic scheduler. Then, for all states $t \in S \setminus \{ final \}$ (see [3] for the proof):

$$ \mathrm {Pr}^{\mathfrak {S}}_t(\bigcirc \Diamond t) \leqslant 1-p_t^{|C_t|-1} \cdot (1-q_t) \leqslant 1-p^{|C_t|-1} \cdot (1-q). $$

Example 3.7

In the Markov chain $\mathcal {C}[p]$ of Example 3.2, we have $\mathrm {Pr}_{s_i}^{\mathcal {C}[p]}(\bigcirc \Diamond s_i) = 1-p^{n-i}$ for $i < n$. If $p \leqslant 1/2$ then $p=p_{s_i}$, $q=q_{s_i}= 1 - p$ and $|C_{s_i}|=n$. Hence, the bounds in Lemma 3.6 are tight for state $s_0$.    $\blacksquare$

We now define the values $\zeta ^*_s(t)$ for variant 1 in two nuances (fine and coarse). The fine variant is based on $\mathrm {Pr}^{\text {ub}}_t(\bigcirc \Diamond t) = 1- p_t^{|C_t|-1}\cdot (1-q_t)$ and $\mathrm {Pr}^{\text {ub}}_s(\Diamond t)=1$:

$$ \zeta ^*_s(t) = \frac{1}{p_t^{|C_t|-1}\cdot (1-q_t)} $$

for $s,t\in S\setminus \{ final \}$. For the final state we put $\zeta ^*_s( final )=1$. The coarse variant is defined analogously, except that we deal with $\mathrm {Pr}^{\text {ub}}_t(\bigcirc \Diamond t) = 1- p^{|C_t|-1}\cdot (1-q)$. Using Lemmas 3.5 and 3.6 we obtain that (${}^{***}$) holds.

Example 3.8

We regard again the Markov chain $\mathcal {C}[p]$ of Example 3.2. For the weight function $wgt$ of $\mathcal {C}[p]$ given by $wgt (s_0)=1$ and $wgt (s_i)=0$, we obtain $e_0^* = 1/p^n$ and $e_{i}^* = 1/p^n - 1/p^i$ for $i=1,\ldots ,n$ (see [3]). The expected number of visits for $s_i$ is $\zeta _{s_0}^{\mathcal {C}[p]}(s_i) = p^{i-n}$. As the states $s_0,\ldots ,s_{n-1}$ constitute an SCC, the fine and coarse variant yield the same bound for the maximal recurrence probability from state $s_0$, namely $\zeta _{s_0}^*(s_i) = 1/p^n$ for all $i<n$. Thus, the starting vector y for the upper value iteration is $(1/p^n,1/p^n,\ldots ,1/p^n,0)$ as $s_0$ is reachable from all states $s \not = final$. In particular, $y_{s_0}=e^*_{s_0}$ is optimal.    $\blacksquare$

If the SCCs are large and their minimal positive transition probabilities are small then the values $\zeta ^*_s(t)$ tend to be very large. Better bounds for the maximal recurrence probabilities $\mathrm {Pr}^{\max }_t(\bigcirc \Diamond t)$ are obtained by the following variant.

Upper Bound for Maximal Recurrence Probabilities (Variant 2). Let $S_0=\{ final \}$. We then define inductively $T_{i-1}=S_0 \cup \ldots \cup S_{i-1}$ and

The assumption $\min _{s\in S} \mathrm {Pr}^{\min }_s(\Diamond final )=1$ yields that if $T_{i-1}$ is a proper subset of S then $S_{i}$ is nonempty. Note that otherwise each state $s\in S \setminus T_{i-1}$ has an action $\alpha _s$ with $P(s,\alpha _s,T_{i-1})=0$. But then $P(s,\alpha _s, S \setminus T_{i-1}) = 1-P(s,\alpha _s, T_{i-1}) = 1$ for all states $s\in S \setminus T_{i-1}$. Let $\mathfrak {S}$ be a memoryless deterministic scheduler with $\mathfrak {S}(s)=\alpha _s$ for all $s\in S \setminus T_{i-1}$. Then, $\mathrm {Pr}^{\mathfrak {S}}_s(\Box \lnot T_{i-1})=1$ for each $s\in S \setminus T_{i-1}$. Hence, $\mathrm {Pr}^{\mathfrak {S}}_s(\Diamond final )=0$ for $s\in S \setminus T_{i-1}$. Contradiction. Thus, $S= T_{k}$ for some $k \leqslant |S|$ and S is the disjoint union of the sets $S_0,S_1,\ldots ,S_{k}$. By induction on $i\in \{0,1,\ldots ,k\}$ we define values $d_t \in \ ]0,1]$ for the states $t\in S_i$. In the basis of induction we put $d_{ final }=1$. Suppose $1 \leqslant i \leqslant k$ and the values $d_u$ are defined for all states $u\in T_{i-1}$. Then, for each state $t\in T_i$ we define:

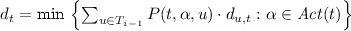
where $d_{u,t}=1$ if $C_t \not = C_u$ and $d_{u,t}=d_u$ if $C_u=C_t$. Recall that $C_t$ denotes the unique SCC containing t and that the values $d_t$ are positive as $P(t,\alpha ,T_{i-1}) >0$ for all actions $\alpha \in Act (t)$. In the appendix of [3] we show:

Lemma 3.9

$\mathrm {Pr}_t^{\max }(\bigcirc \Diamond t) \ \leqslant \ 1 - d_t$ for each state $t \in S$

Using Lemma 3.5 and Lemma 3.9, condition (${}^{***}$) holds for $\zeta ^*_s(t) = 1/d_t$.

Example 3.10

Again, consider the Markov chain $\mathcal {C}[p]$ of Example 3.2. For the weight function given by $wgt (s)=1$ for $s \not = final$, we obtain $e_{i}^* = (1-p^{n-i})/(p^n(1-p))$. With the first variant, we get the starting vector y for the upper value iteration where $y_{s_i} = n/p^n$ for all states $s_i$ with $i < n$. The second variant generates the decomposition $S_i=\{s_{n-i}\}$ for $i=0,1,\ldots ,n$. Then $\zeta ^*_{s_0}(s_i) = \zeta ^{\mathcal {C}[p]}_{s_0}(s_i)$ as $\mathrm {Pr}^{\mathcal {C}[p]}_{s_0}(\Diamond s_i)=1$ and $\mathrm {Pr}_{s_i}(\bigcirc \Diamond s_i) = 1-p^{n-i}$ (see Example 3.7). Thus, the computed bound for the expected times to visit $s_i$ is the exact value $\zeta ^*_{s_0}(s_i) = d_{s_i} = \ p^{i-n}$. Here, index i ranges between 0 and $n-1$. Thus, the second variant generates the starting vector y where $y_{s_i} = \sum _{j=0}^{n-1} p^{j-n} = (1-p^n)(p^n(1-p))$ for all states $s_i$ with $i < n$, which is optimal for $i=0$.    $\blacksquare$

4 Topological Interval Iteration

To increase the efficiency of the value iteration, several authors proposed a stratified approach that exploits the topological structure of the MDP [11, 13, 14]. In such a topological value iteration, for each strongly connected component (SCC) a value iteration is performed, which only updates the values for the states in this particular SCC. As the SCCs are computed in their topological order from the bottom up, values for the outgoing transitions of the current SCC have already been computed. For models with more than one SCC, this approach has the potential to reduce the number of state updates that are performed, as it avoids updating the values for every state in each iteration step.

To adapt such a topological approach to interval iteration, the main challenge is to ensure that the computed upper and lower bounds for the states in a given SCC S are suitably precise to allow their effective utilization during the interval iteration computation in those SCCs containing states that can reach S and thus potentially depend on its values. While we formalize our approach for the setting of maximal expected accumulated weights, the presented approach can be easily adapted to a topological interval iteration for the computation of extremal reachability probabilities in the setting of [18].

Given a subset of states $Q \subseteq S$ and, for each state $q \in Q$, an upper bound $u_q$ and a lower bound $l_q$ for the value $e^{*}_{\mathcal {M},q} = e^*_q$, i.e., $l_q \leqslant e^{*}_{\mathcal {M},q} \leqslant u_q$, we induce two new MDPs that arise by discarding all transitions of the states $q\in Q$ and adding a new transition from q to a trap state with weight $l_q$ resp. $u_q$. Formally, we construct an MDP $\mathcal {M}_\uparrow = (S, Act ',P', final , wgt _\uparrow )$ incorporating the upper-estimate and an MDP $\mathcal {M}_\downarrow = (S, Act ',P', final , wgt _\downarrow )$ incorporating the lower estimate. We introduce a fresh action $\tau$, i.e., $Act ' = Act \cup \{\tau \}$, which is the only action enabled in the Q-states and goes to $final$ with probability 1, replacing the original actions, i.e., $P'(s,\alpha ,t)=P(s,\alpha ,t)$ for all states $s \notin Q$, $\alpha \in Act$, $t \in S$ and, for all states $q \in Q$, $P'(q,\tau , final )=1$ and $P'(q,\alpha ,t)=0$ for all $\alpha \in Act$, $t \in S$. The MDPs $\mathcal {M}_\uparrow$ and $\mathcal {M}_\downarrow$ differ in their weight functions, with $wgt _\uparrow (q,\tau ) = u_q$ and $wgt _\downarrow (q,\tau ) = l_q$ for $q \in Q$ while the weights for the remaining state-action pairs remain unchanged, i.e., $wgt _\uparrow (s,\alpha ) = wgt _\downarrow (s,\alpha ) = wgt (s,\alpha )$ for all $s \in S \setminus Q$ and $\alpha \in Act$. Intuitively, the $\tau$ transitions simulate the expected weight accumulated on the path fragments from states $q \in Q$ until $final$, replacing it with the upper or lower bound, respectively. As $\mathrm {Pr}^{\min }_{\mathcal {M}}( \Diamond final ) = 1$, we also have $\mathrm {Pr}^{\min }_{\mathcal {M}_\uparrow }( \Diamond final ) = \mathrm {Pr}^{\min }_{\mathcal {M}_\downarrow }( \Diamond final ) = 1$.

Lemma 4.1

With the notations as above (see [3] for the proof):

• (a) $e^{*}_{\mathcal {M}_\downarrow ,s} \; \leqslant \; e^{*}_{\mathcal {M},s} \; \leqslant \; e^{*}_{\mathcal {M}_\uparrow ,s}$ for all states $s \in S$

• (b) If $|u_q - l_q| < \varepsilon$ for all $q \in Q$, then $|\; e^{*}_{\mathcal {M}_\uparrow ,s} - e^{*}_{\mathcal {M}_\downarrow ,s} \;| < \varepsilon$ for all $s \in S$.

We are now interested in performing an interval iteration in the setting where we are given a desired precision threshold $\varepsilon$ and lower and upper estimates $l_q$ and $u_q$ for a subset of states. Here, we assume that the bounds are within the desired precision, i.e., that $|u_q - l_q| < \varepsilon$ and that $l_q \leqslant e^{*}_{\mathcal {M},q} \leqslant u_q$. As these estimates will arise from the processing of previously handled SCCs, we can ensure that the desired precision is indeed obtained. Let $\mathcal {M}_\downarrow$ and $\mathcal {M}_\uparrow$ be the two MDPs that are induced by applying the transformation detailed above for the two estimates, respectively. We now perform an interval iteration, but instead of performing both iterations in the original MDP $\mathcal {M}$, the iteration from above is performed in $\mathcal {M}_\uparrow$ and the iteration from below is performed in $\mathcal {M}_\downarrow$ in an interleaved fashion.

Let $x_s$ and $y_s$ be lower and upper bounds for $e^{*}_{\mathcal {M},s}$, i.e., with $x_s \leqslant e^{*}_{\mathcal {M},s} \leqslant y_s$ for all $s \in S$, for example computed using the methods detailed in Sect. 3.3. We obtain starting vectors $x^{(0)}$ (for the value iteration from below in $\mathcal {M}_\downarrow$) and $y^{(0)}$ (for the value iteration from above in $\mathcal {M}_\uparrow$) by setting

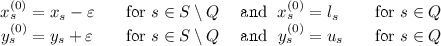
To ensure that $x^{(0)}_s$ is indeed a lower bound for $e^{*}_{\mathcal {M}_\downarrow ,s}$ for the states $s \in S \setminus Q$, we subtract $\varepsilon$. Lemma 4.1(b) together with Lemma 4.1(a) yields $e^{*}_{\mathcal {M}_\uparrow ,s} - e^{*}_{\mathcal {M}_\downarrow ,s} < \varepsilon$, and as $e^{*}_{\mathcal {M}_\uparrow ,s}$ is an upper bound for $e^{*}_{\mathcal {M},s}$ we have $e^{*}_{\mathcal {M},s} - e^{*}_{\mathcal {M}_\downarrow ,s} < \varepsilon$. Then, due to the assumption that $x_s \leqslant e^{*}_{\mathcal {M},s}$, it is guaranteed that $x_s - \varepsilon \leqslant e^{*}_{\mathcal {M}_\downarrow ,s}$. For the upper bound $y^{(0)}_s$ similar arguments apply when adding $\varepsilon$ to the upper bound computed for $e^{*}_{\mathcal {M}}$.

The topological interval iteration for $e^{*}_{\mathcal {M}}$ and precision $\varepsilon$ now works as follows. We first compute lower and upper bounds $x_s$ and $y_s$ for $e^{*}_{\mathcal {M},s}$ for all states in $\mathcal {M}$ (see Sect. 3.3). We then apply standard algorithms to compute a topological ordering $C_1, C_2, \ldots , C_n$ of the SCCs of $\mathcal {M}$. We then process each SCC according to the topological ordering, from the bottom up. We maintain the set Q of states that are contained in SCCs that have already been processed, as well as upper bounds $u_q$ and lower bounds $l_q$ for these states satisfying $u_q - l_q \leqslant \varepsilon$. The order of processing ensures that the successor states for all transitions that do not lead back to the current SCC are contained in Q. Let $C_i$ be the current SCC. If it is a singleton SCC, i.e., containing just a single state s, we can derive $u_s$ and $l_s$ directly. In particular, for the $final$ state we can set both values to 0. For non-singleton SCCs, we consider the sub-MDP $\mathcal {M}_i$ of $\mathcal {M}$ containing the states in $C_i$ as well as all states not in $C_i$ but reachable from $C_i$. The latter states are all contained in Q. We then perform the interleaved interval iteration in $\mathcal {M}_\downarrow$ and $\mathcal {M}_\uparrow$ derived from $\mathcal {M}_i$ with the starting vectors derived from $x_s$ and $y_s$ and the stopping criterion $y^{(n)}_s - x^{(n)}_s < \varepsilon$ for all $s \in C_i$. Termination for $C_i$ will eventually occur as shown in [3]. Subsequently, we add all states $s \in C_i$ to Q and set $l_s = x^{(n)}_s$ and $u_s = y^{(n)}_s$. Having processed the SCC $C_i$, we proceed with the next SCC in the topological order. Once all SCCs are processed, we return the vectors $(l_s)_{s \in S}$ and $(u_s)_{s \in S}$, which contain lower and upper bounds for the values $e^{*}_{\mathcal {M},s}$ with precision $\varepsilon$. The correctness of the output follows from repeated application of the termination and correctness proof for individual SCCs (see [3]).

5 Implementation

We have implemented the algorithms presented in this paper as an extension of the PRISM model checker [25]. PRISM contains four major engines: an $\textsc {Explicit}$ engine and three other engines ($\textsc {Mtbdd}$, $\textsc {Hybrid}$, $\textsc {Sparse}$) that either partially or fully rely on symbolic, MTBDD-based methods [28].

Interval Iteration. Since the performance of the different engines varies across benchmarks, we have implemented interval iteration for all four, extending the existing value iteration based implementations for computation of (extremal) expected accumulated rewards and reachability probabilities in MDPs. More complex probabilistic model checking problems often use these as a basic building block. Consequently, our interval iteration implementation is automatically used there as well, for example in the context of LTL model checking. We also implement interval iteration for discrete-time Markov chains (DTMCs), a special case of MDPs, to facilitate further benchmarking. We assume non-negative weights (rewards/costs), a limitation imposed by PRISM.

Our implementation supports, in addition to standard value iteration updates, two other well known variants that are implemented in PRISM for the standard value iteration approach as well: Jacobi-like updates (directly solving self-loop probabilities) and Gauss-Seidel-like updates. The latter are limited to the $\textsc {Explicit}$ and $\textsc {Sparse}$ engines due to the difficulty of a symbolic implementation.

To be able to apply interval iteration for the computation of maximal reachability probabilities, we support the quotienting of maximal end components as proposed in [18]. This is required to ensure that the upper value iteration converges. Interval iteration for minimal expectations is currently only supported for the $\textsc {Explicit}$ engine and if the MDP after preprocessing is contracting (this is always true for the special case of DTMCs).

Upper Bound Computation. For (extremal) reachability probabilities, the upper bound (=1) and lower bound (=0) for the interval iteration is set directly. For the (extremal) expected accumulated reward computation, we set the lower bound to 0, and support variant 1 (coarse and fine) and variant 2 of the upper bound algorithms of Sect. 3.3, computing a single upper bound for all states (i.e., using $R_s=S$). For minimal expectations, we use the bound obtained for from one of the variants, and can additionally obtain an upper bound using the Dijkstra Sweep for Monotone Pessimistic Initialization (DS-MPI) algorithm for obtaining upper bounds on the minimal expectations proposed in [27], which we implemented for the $\textsc {Explicit}$ engine.

Topological Iteration. Lastly, we also implemented both topological value iteration and topological interval iteration (see Sect. 4) in the $\textsc {Explicit}$ engine.

6 Experiments

We have carried out extensive experiments using the PRISM benchmark suite [26], considering 294 model/property combinations in total. We give here an overview of the results; further details can be found in the appendix of [3].

Accuracy. To gauge the prevalence of imprecise results due to early termination of value iteration, we have compared the PRISM results for the benchmark instances against an exact result (if available) or the result obtained by interval iteration. We use $\varepsilon = 10^{-6}$ and evaluate both absolute and relative mode.⁵ Comparing the interval iteration results against the exact results (where available) demonstrated that the interval iteration results indeed have the expected precision. We say that a value iteration result has a precision of less than $10^{-x}$ if the difference between the result and the reference value is larger than $10^{-x}$. When the computations are done using relative termination checks, the precision is also computed relatively. For absolute mode, the results of 67 of the 294 instances were less precise than $10^{-6}$ (44 less precise than $10^{-5}$, 17 less than $10^{-4}$ and 2 less than $10^{-3}$, none of the benchmark instances had a precision of less than $10^{-2}$). Detailed statistics, for relative mode as well, can be seen in Table 1, which shows the overall results of our accuracy check. A similar picture arises with the relative termination check, however here the absolute imprecision is magnified for values larger than 1.

Table 1. Results of the accuracy benchmarks, split into the instances with probability and expectation properties and whether comparison was against exact or interval iteration results. Note that instances with precision less than $10^{-3}$ are also included in the count for $10^{-4}$, etc.

The largest imprecision occurred for the “coin2.nm” model of the “consensus” case study (with model parameter $K=16$) and the “steps-max” expectation property. The exact result for this instance is 3267. In absolute mode, the value iteration had the result 3266.9986814425756, while interval iteration had 3267.0000004994463. In relative mode, the imprecision is magnified in absolute terms, i.e., the value iteration has the result 3262.69160811823 while interval iteration yielded 3267.0016321821013. As can be seen here, interval iteration yielded the expected precision, i.e., 6 correct fractional digits for absolute mode and 6 correct first digits in relative mode. The second instance with precision of less than $10^{-3}$ is for the same model but the “steps-min” property.

Overall, for the benchmark instances, the imprecision was not as grave as for the example from [18]. However, in independent work on a simplified probabilistic model of an error handler, inspired by [24], we encountered a non-artificial model with probability results of 0.328597 (value iteration) vs 0.687089 (interval iteration), with $\varepsilon = 10^{-6}$. For details, see [3].

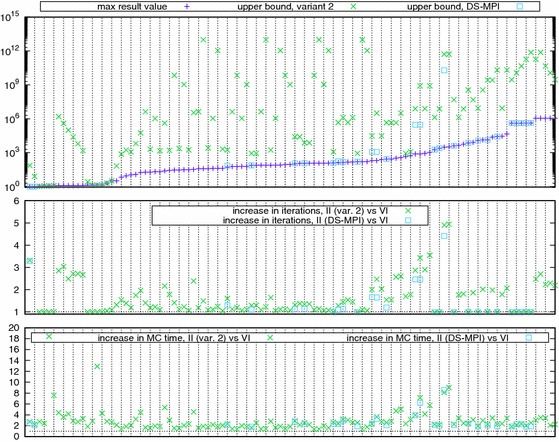
Quality of Upper Bounds and Cost of Interval Iteration. In another experiment, we were interested in (1) the quality of the upper bounds obtained by the various heuristics and (2) in the impact of using interval iteration (II) instead of value iteration (VI). Figure 3 shows statistics for a comparison of the variant 2 and the DS-MPI upper bound heuristics (for minimal expectations in MDPs and expectations in DTMCs) for the benchmark instances using expected rewards, $\varepsilon =10^{-6}$ and a relative termination check.

The upper plot shows upper bounds, compared to the maximal (finite) value in the result vector. Clearly, no upper bound can be below that value. The benchmark instances here are sorted by this maximal result value. The plot in the middle then shows the increase in the number of iterations that are carried out for interval iteration compared to value iteration, e.g., an increase of 2 signifies that interval iteration required twice the number of iterations. Note that we count the upper and lower iteration step as a single combined iteration. To simplify the presentation, the plot in the middle omits a single data point, consisting of a 32-fold increase from 5 to 159 iterations. The plot at the bottom of Fig. 3 shows the corresponding increase in the time for model checking (including precomputations, upper bounds computations and iterations). In this plot, instances where all times are below 1 s are omitted due to their limited informative value.

Fig. 3.

Top: maximal result value versus the upper bounds. Middle: increase (2 = double, ...) in the number of iterations. Bottom: increase in model checking time. The x-axis of the plots represents the model/property instances, sorted by maximal result value.

Fig. 4.

Number of multiplication operations for (topological) value and interval iteration. The x-axis of both plots represents the model/property instances, sorted by the number of multiplication operations for plain value iteration.

Generally, an increase in the number iterations required for interval iteration compared to value iteration can be due to the lower iteration requiring more iterations to reach a precise result or due to the number of iterations required by the upper iteration to converge from the initial upper bound. As can be seen, the DS-MPI heuristic (where applicable) generally provides much better upper bounds than variant 2, often by several orders of magnitude. However, for the benchmark instances, the number of required iterations does not rise by a similar factor, indicating a certain insensitivity to the quality of the upper bound. Generally, the increase in iterations for interval iteration can be considered benign. For the model checking times, a certain increase can be seen, which is to be expected due to the additional work carried out. The largest relative increases (on the left of the plot) are for instances where value iteration took less than 1 s, while in general the increases remain modest.

In [3], we also evaluate the variant 1 heuristic. The bounds obtained using this variant in general tend to be significantly larger and roughly half of the benchmark instances had no variant 1 bound that could be represented as a double-precision floating point number. However, there are instances where the variant 1 and variant 2 bounds coincide and where the variant 1 computation is faster. Additionally, we present and discuss similar experiments for the benchmark instances using probability computations. For those, the increase in the number of iterations (and model checking time) is even more limited due to the a priori availability of a rather good upper bound of 1 for probabilities.

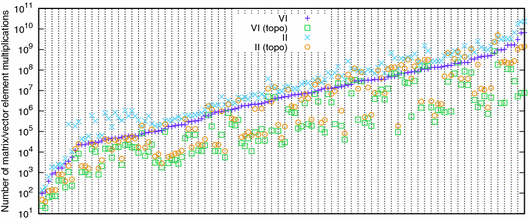
Topological Iteration. Figure 4 shows statistics of experiments comparing topological iteration against plain iteration. We considered the MDP benchmark instances, using $\varepsilon = 10^{-6}$ and absolute checks. As the topological approach does not process all states in each iteration, we need a more fine grained measure of the operations: The plot depicts the number of matrix element/vector element multiplications, e.g., the operations $P(s,\alpha ,t) \cdot v_t$ for MDPs and non-zero matrix entries. The potential for the topological approach is clearly demonstrated, with a reduction in the required multiplications often by an order of magnitude or more. In general, such a reduction translates into a decreased running time as well. Our experiments thus show that the known potential for topological value iteration (see, e.g., [11]) transfers to topological interval iteration as well.

7 Conclusion

In this paper, we have shown that interval iteration is a viable approach to deal with the potential termination criterion problems raised by [18], providing higher confidence in the correctness of the results of probabilistic model checkers. In particular, we have shown how the approach of [18] can be successfully extended for the context of expected accumulated weights. Clearly, even those situations where the results obtained using the standard value iteration termination criterion (or some particular parameter setting) happen to be sufficiently precise are rendered problematic in practice due to the absence of any precision guarantees. Even with interval iteration, the orthogonal question of the precision of the underlying floating-point computations remains and could be addressed by maintaining bounds on their precision. In future work, we intend to extend the implementation, e.g., using the additional knowledge provided by interval iteration in threshold problems. Additionally, the upper and lower iterations can be carried out in parallel, reducing the performance impact.

We will also focus on extending our results for the setting of non-contracting MDPs. In the case of non-negative weights, our implementation for maximal expectations handles non-contracting MDPs thanks to the preprocessing proposed in [16], while for minimal expectations the vector obtained using DS-MPI could be used as an upper starting vector, as [7] establishes the unique fixed-point characterization and convergence of value iteration under relaxed assumptions even for general weights. For general weighted MDPs, checking finiteness of the expected weight is more involved. Our results on lower and upper bounds for expectations might also be interesting for different purposes, e.g., in the context of planning as outlined in [27].