
速度には光速という限界があるけれど、加速度に限界はないのか?
X(旧Twitter)で、物理に真剣に向き合おうとする学生からの興味深い質問を見つけました。それは「速度には光速という限界があるけれど、加速度には限界がないのか?」というものです。
相対性理論によれば、物体の速度は光速度cを超えることができないことがよく知られています。この制限は、速度のx成分、y成分、z成分のいずれにも適用され、そして速度の大きさ自体もcを超えることはありません。
では、速度ではなく「加速度」についてはどうでしょうか?加速度にも上限が存在するのかという問いは、物理学の最先端の観点から見ても非常に意義のある問題です。
この加速度の問題を考える上で、便利な「次元」という概念をまず説明します。物理学では、さまざまな物理量が「次元」という特性を持っています。この次元は、空間の自由度を表す幾何学的な次元とは異なり、物理量の性質を示すものです。たとえば、ある物体の「長さ」という量は、メートルやフィートといった単位によって数値は異なりますが、どの単位で表現しても「長さの次元」であるとみなされます。この場合、次元を統一的に扱うために、物理量とその単位を [ ] の中に記述します。たとえば、[1 メートル]=[10メートル]=[1マイル]=[3マイル]=[1フィート]などの等式が、長さの次元の観点では成立します。
この次元の考え方は「次元解析法」と呼ばれ、物理学における解析において非常に有用です。この概念を用いれば、加速度の上限についても理論的な枠組みで検討できるようになります。
加速度の上限の問題に戻りましょう。もし加速度に有限の上限が存在するとすれば、その値の次元は「加速度の次元」と一致する必要があります。さらに、その上限値が光速c、プランク定数 ℏ、重力定数Gなどの自然定数によって決まるのならば、それらの自然定数の適切な組み合わせで、その上限値を表現できるはずです。そこで候補として挙がるのが、下記の「プランク加速度」です。

この大きさの加速度が関与する領域で実験を行うと、量子重力の効果が無視できなくなると予想されます。これは、量子重力理論が重要になる閾値としても注目されるポイントです。たとえば、超弦理論のような量子重力理論では、このプランク加速度の値付近で、物理の描像が劇的に変化する可能性があります。また、プランク加速度を超える加速度が実現しない可能性を考えるのも、物理として健全なアプローチだと言えるでしょう。
しかし、次に述べるように、超弦理論を含むローレンツ不変性を保つ量子重力理論では、加速度に明確な上限が存在しないと考えられています。
加速度を論じるために、ここで思い出すべきこととして、量子力学において「力」という概念そのものが曖昧だということがあります。古典力学で近似できる特定の条件下でしか「力」を論じることができません。古典論では、力は「質量 × 加速度」として表されますが、量子力学では力の定義が曖昧になるため、加速度の概念自体も明確に定義できなくなります。これは、相対論的な量子力学での枠組みの中でも同様です。
量子力学では「力」の代わりに現れるのが「力積」です。この力積は、運動量の変化分として量子力学でも定義可能な概念です。具体的には、運動量の変化分を測定することで、その変化にかかった時間Δtと作用した力の積が分かるとします。
後で述べる衝撃波での設定のように、もしΔtを明確に定義できる実験環境を構築できれば、その範囲内で力積から「力」を近似的に定義し、さらにそれから「加速度」を計測することも可能です。したがって、量子力学においても、特定の条件下では古典力学に基づく「力」や「加速度」を論じる道筋が示されることになります。

この運動量の大きさにも次元解析から、下記の「プランク運動量」と呼ばれる値が定義されています。

ここで、キログラム (kg)、メートル (m)、秒 (s) の単位を用いてプランク運動量を換算すると、その大きさはせいぜい10程度に過ぎません。この値は、日常的な物体が通常持つ運動量とそれほど変わりません。しかし、この規模の運動量を非常に軽い質量を持つ物体、たとえば電子が持つ場合、その運動量に対応する速度は光速度cに極めて近いことがわかります。
ローレンツ対称性を満たす相対論的な理論では、電子のような粒子がプランク運動量をはるかに超える運動量を持つことも許容されます。たとえば、ある慣性系で静止している電子であっても、ローレンツ変換で関連付けられる別の慣性系では、その運動量がプランク運動量を大きく超える値を持つことが分かります。具体的には、4元運動量ベクトルに対するx方向のローレンツ変換は次のように表されます。

上の式に現れるローレンツブーストのパラメータ ξを非常に大きくすると、運動量のx成分はプランク運動量を超えることが可能になります。したがって、ローレンツ対称性を持つ理論では、そのように大きな運動量を持つ粒子の状態を実際に作り出すことができます。このとき、プランク運動量がその状態の存在を特に妨げることはありません。この点は、加速度の上限を考える際にも重要なポイントとなります。
さて、ここで、電子をx方向に進む電磁衝撃波によって加速する実験を考えてみましょう。この状況を記述するための電磁場は、マクスウェル方程式を満たす必要があります。その4次元電磁ポテンシャルは、次のように与えられます。
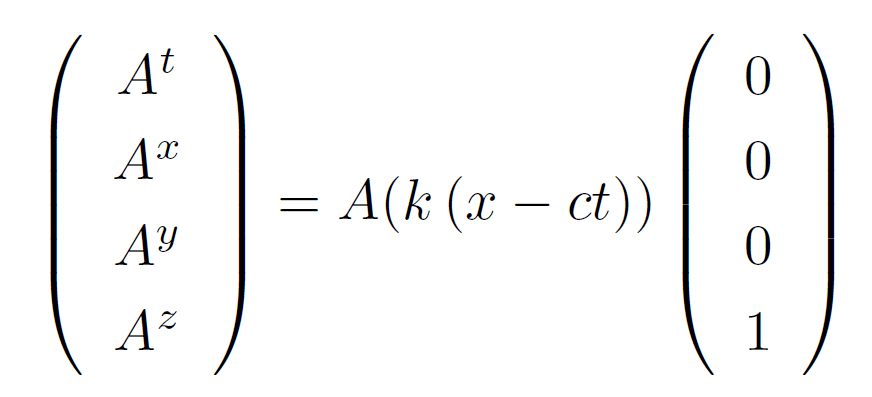
ここでkは長さの逆数の次元をもつ正の値をとります。また右辺に現れる関数A(x)は自由にとっても、上の電磁ポテンシャルはマクスウェル方程式の解になります。そこで図1のように、幅δxの中に局在をした波を考えましょう。

ここで相対論のローレンツ変換

に対する不変性を理論に課してみます。(2)式右辺のξは、任意の実数値をとります。そして電磁ポテンシャルは

のように、ローレンツ変換を受けます。これから(1)式の解は

に変換後にはなります。したがってξを大きな正の値にとった場合は、図2のように波の幅はローレンツ収縮を受けて極めて小さくなります。

理論がローレンツ対称性をもつということは、元の慣性系(t,x)においてさえも、このような幅の小さな衝撃波を用意できることを意味します。
ここで、元の慣性系(t,x)において止まっている電子に、この幅が極めて小さな衝撃波を衝突させて、電子を加速させてみましょう。(簡単のため、電子の運動によって新たに励起される電磁場はここでは無視します。)
電子が散乱される時間はΔt=δx'/cで評価されます。そしてξを大きくすると、このΔtは極めて小さくなります。そして散乱後の電子の運動量は典型的には

と評価され、ξを大きくすると発散していきます。
この場合、電子が電磁波と散乱した後の運動量から、散乱前の運動量(止まっている電子では零)を引くことで、電子の運動量の変化分を求めることができます。
この運動量の変化分は、古典論でも量子論でも同様の考え方で扱われます。ただし、量子論の場合、この変化分は確率的な分布を持つため、変化量が一意に定まるわけではありません。その代わり、分布の期待値を用いて、この運動量変化分が与えられているものとします。
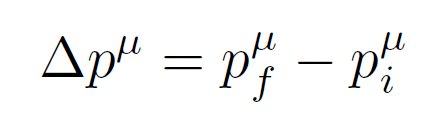
ここで上で述べた(5)式からx方向の運動量の変化分も、限界なく発散できます。

つまり、「力積」に対応する運動量の変化量は、限界なく大きくなることがわかります。同時に、散乱時間Δtは短くなるため、この運動量の変化量から評価される加速度にも上限が存在しないことが示されます。
したがって、理論に相対論的なローレンツ対称性が含まれている場合、加速度に上限値を設定することは不可能です。超弦理論やその他の共変的なカットオフを取り入れた理論において、加速度に上限は現れません。
(註:相対性理論では、時間と空間を一体化した「時空」という概念を用います。たとえば、z軸周りの空間回転対称性では、x座標とy座標が混ざっても、回転後の物理法則は変わりません。同様に、時間tとx座標が混ざるローレンツ変換の前後でも物理法則が変わらない性質を「ローレンツ不変性」と呼びます。
カットオフとは、ある量が無限に大きくなれず、ある一定の値を超えることができない場合に、その閾値を指します。そして、ローレンツ不変性を保ちながら導入されるカットオフを「共変的なカットオフ」と呼びます。超弦理論も、このような共変的なカットオフを備えています。
たとえば、相対論的な電子の運動量に対して共変的なカットオフΛを導入することは容易です。図3のように、このカットオフは、四元運動量ベクトルの2乗が Λの2乗以下となるように設定できます。たとえば、カットオフ Λをプランク運動量Pの値に設定することも可能です。このΛが存在しても、運動量の空間成分自体は実数の範囲で自由に取ることができ、プランク運動量そのものは、限界としての重要な意味を持ちません。)


なお時空を格子状に離散化した非共変的な理論では、加速度の上限が現れる可能性はあります。
さらに、(1)式で示される電磁ポテンシャルを用いた電磁波で非常に強い加速を試みた場合、強い電場による電子・陽電子の対生成、いわゆる「シュヴィンガー効果(Schwinger effect)」を懸念する方もいるかもしれません。しかし、実際には(1)式のような特定の形の波からは、自発的な粒子生成が起こることはありません。これは、ローレンツ不変性とエネルギー・運動量保存則から示される事実です。そのため、(1)式のような強い電場や磁場を伴う波についてシュヴィンガー効果を無視しても問題はありません。
追記(2025/1/7):ToruMuse’icさん(@ToruMuseic)のご指摘により、説明の不備を改良しました。
いいなと思ったら応援しよう!

