Abstract
pH is an important parameter in condensed-phase systems, because it determines the protonation state of titratable groups and thus influences the structure, dynamics, and function of molecules in solution. In most force field simulation protocols, however, the protonation state of a system (rather than its pH) is kept fixed and cannot adapt to changes of the local environment. Here, we present a method, implemented within the MD package GROMACS, for constant pH molecular dynamics simulations in explicit solvent that is based on the λ-dynamics approach. In the latter, the dynamics of the titration coordinate λ, which interpolates between the protonated and deprotonated states, is driven by generalized forces between the protonated and deprotonated states. The hydration free energy, as a function of pH, is included to facilitate constant pH simulations. The protonation states of titratable groups are allowed to change dynamically during a simulation, thus reproducing average protonation probabilities at a certain pH. The accuracy of the method is tested against titration curves of single amino acids and a dipeptide in explicit solvent.
1. Introduction
Together with temperature, pressure, and ionic strength, pH is one of the key parameters that determine the structure and dynamics of proteins in solution. Most notably, many proteins denature at low pH values,(1) and aggregation, such as formation of amyloid fibrils in Alzheimer’s disease(2) and insulin aggregation,(3) is pH-dependent. Because the function of a protein depends on its structure, pH is critical for protein function. Examples of pH-dependent regulation of protein function are the pH-controlled gating of membrane channels,4−6 or activation of influenza virus in host cells.(7)
pH affects protein structure, because the protonation state of the ionizable groups of a protein depends on pH, in particular histidine amino acids for which the proton affinity (pKa) is very close to the physiological pH. Mainly via its charge, the protonation state of each ionizable group influences, in turn, the physicochemical properties of proteins, their structure, and their function.
Despite its relevance to biomolecular structure and function, pH and changes of protonation state of titratable groups of a protein are usually not described in computer simulations. Typically, a structure with fixed protonation states is used, chosen according to the most probable protonation arrangement at a given pH. This choice is often not straightforward, because hydrogens are usually not resolved in X-ray crystallography and the acid dissociation constant (Ka) values of the ionizable groups, in most cases, are not known. Therefore, the protonation state must be inferred from NMR(8) or spectroscopic data,(9) or from electrostatic calculations (e.g., Poisson–Boltzmann (PB)10,11 or Generalized Born(12) approaches). Furthermore, changes in the protonation state, either due to a change in the environment pH or in the protein conformation, as well as equilibrium protonation fluctuations leading to fractional protonation probabilities, are not taken into account by conventional simulations. As a consequence, the understanding of many biological phenomena, which involve a redistribution of charge, such as ligand binding reactions inducing a proton redistribution,15,16 peptide insertion in membranes (e.g., fusion peptides),13,14and pH-dependent conformational changes,2,6 would greatly benefit from a dynamic description of the protonation states.
Several attempts have been made to overcome these limitations. The most-accurate way of modeling (de)protonation events is to describe the system at a quantum mechanics level, where the electronic structure responds to changes in the local environment. However, these calculations are very expensive, in terms of computational cost. This drawback has been partly overcome in mixed quantum mechanics/molecular mechanics approaches,(17) where only the ionizable groups of the protein are treated at the quantum level.
Computationally more affordable approaches to describe proton transfer events are EVB18−21 and QHOP(22) methods. Here, the potential energy surface on which protons move is parametrized by ab initio calculations, whereas the rest of the system is described by a molecular mechanics force field.
A complication common to these approaches is that the equilibrium state is generally reached at time scales that are much slower than those accessible to molecular dynamics (MD) simulations. This is particularly true for protein systems, where typical deprotonation times of ionizable groups in the interior of a protein are microseconds or slower.(23) As a consequence, enhanced sampling of the transitions between the protonated and deprotonated state is particularly relevant for simulations of protein systems. For the aforementioned approaches, however, there is no obvious way how to enhance proton transfer rates.
A further problem concerns the proper description of the pH of a solution. The average hydronium concentration in a typical simulation box can be described by a time average, as well as via an ensemble average. In the case of a time average, because of the fact that the concentrations of hydronium considered are low, typically pH 7, it might require very long simulation times to sample the hydronium distribution in the solution. In the case of the ensemble average, however, unpractically large simulation boxes would have to be considered, as, for example, for a typical simulation box of ∼30 000 water molecules, one hydronium ion already corresponds to a pH of ∼2–3, thus increasing the computational cost of the calculation.
To address these issues in the context of force field simulations, several approaches have been proposed, all of which use a titration coordinate λ, which describes the protonation state of a certain ionizable group. For example, values of λ = 0 and λ = 1 correspond to the protonated and deprotonated states of a titratable group, respectively, as will be used in this work. Two main categories of approaches can be distinguished depending on the nature−discrete or continuous−of this titration coordinate.(24)
A discrete titration coordinate is typically used by methods combining MD and Monte Carlo (MC) simulations for the sampling of the protonation reaction coordinate. At intervals during the MD simulation, a MC step is performed, in which the protonation state of a residue is changed. The acceptance criterion to keep the new protonation state is based on the protonation free energy of the titratable group, which is computed at every MC step. The major differences between the approaches in this category concern the way that this free energy is computed. In the approaches of Baptista and co-workers,(25) Dlugosz and Antosiewicz(26) and Mongan and Case,(12) the contribution of each protonation state to the protonation partition function is evaluated, and the protonation free energy (and pKa) is then obtained from the partition function. Because all possible protonation states of the system have to be considered, the computational effort formally scales exponentially (2N) with the number of titratable sites in the system (N). In practice, however, MC sampling and cutoffs are applied to reduce computational effort. To estimate the free energy of each state, implicit solvent Poisson–Boltzmann (PB)25,26 or Generalized Born(12) approaches are used. The use of continuum approximations in the estimation of protonation free energies has the advantage of reducing degrees of freedom of the system. However, to describe more-complex systems, such as membrane proteins, or systems such as channels for which explicit water molecules are crucial, continuum solvent models are of limited use.
In contrast, Bürgi et al. suggested to evaluate the protonation free energy at the MC step by a short thermodynamic integration (TI) simulation.(27) However, the cost of the free-energy calculation step can become significant, because it has to be evaluated at each trial. Also, inclusion of interactions between titratable sites is difficult.
In contrast to MD/MC simulations, in the second category of approaches, the titration coordinate λ is allowed to change continuously between the protonated and deprotonated states. Börjesson and Hünenberger28,29 developed the “acidostat” method, where the extent of deprotonation is relaxed to equilibrium by weak coupling to a proton bath in a way similar to methods for constant temperature and pressure.(30) Equilibrium fluctuations of the protonation states are not described, and each site thus experiences the average effect of the others.
In a different approach, introduced by Merz and Pettitt,(31) the continuous λ coordinate is treated as an additional particle of the system, which is propagated in time, according to the equations of motion. The potential of the system is coupled to the chemical potential, which is a function of pH, of the reactants and of the products. Along the same lines, the successive λ-dynamics approach(32) and λ-adiabatic free-energy dynamics(33) treat λ as a dynamical variable in the Hamiltonian. In particular, the λ-dynamics approach was applied to constant pH simulations in implicit solvent by Lee et al.(34) and Khandogin and Brooks.35,36 In their approach, the potential energy landscape, which drives continuous changes of λ, is modulated by the potentials of isolated model titratable groups, and by the pH. Protons are not transferred explicitly to bulk water, forming H3O+; rather, similar to the acidostat of Börjesson and Hünenberger,28,29 the proton-solvation contribution to the force acting on λ is implicitly taken into account. Because this contribution depends on pH, by setting the pH parameter in the simulation, the effect of the proton concentration is included. Coupling between titratable sites, described by multiple λ particles, is implicitly taken into account via the potential energy landscape. In principle, linear scaling of the calculation with the number of protonatable sites is achieved. Because of the continuous character of the titration coordinate, fractional λ values can occur, which correspond to a partially protonated state. To decrease the population of these unphysical states, a barrier potential is used.(34) This is introduced as a separate parabolic function centered at λ = 0.5.(34) Alternatively, ad hoc nonlinear interpolation schemes between the potentials of the end states sampled by λ have been used to decrease the population of intermediate λ values, and thus obtain minima at λ = 0 and λ = 1.(33)
As seen, most of the approaches for constant pH simulations both in the first and second category rest on an implicit description of the solvent. We are not aware of any fully atomistic description that (i) achieves sampling of the relevant space of the titration coordinate (i.e., the physically meaningful end states) and (ii) allows one to control the protonation/deprotonation rate.
In this work, we develop and test a framework to describe changes in protonation states at constant pH that meets all of these requirements. Our method extends the λ-dynamics approach of Brooks and co-workers32,34,35 by introducing a new coupling scheme to describe chemically coupled titratable sites, such as those on the side chain of histidine. Both pH and, via the height of the barrier potential, the protonation rates can be controlled to either reflect experimental proton transfer rates, if available, or to enhance sampling of the protonation space. The method has been implemented within the MD package GROMACS.37−39
To test our method, the titration behavior of simple systems in an explicit solvent was analyzed. First, we considered glutamic acid with neutral termini. To provide a simple example of interactions that can occur in a protein environment, a small dipeptide of sequence Glu-Ala was simulated. Because of its importance in protein systems, imidazole and histidine were chosen as a test case for chemically coupled titratable sites. Finally, the effect of different temperature coupling schemes and different barrier potential heights on deprotonation/protonation rates was assessed.
2. Theory
To clarify the notation, we will first summarize the thermodynamic integration and λ-dynamics approaches. Subsequently, we will describe and develop the building blocks of our approach. First, we will describe how the interval sampled by the titration coordinate λ is constrained, to describe the protonated and deprotonated states of the system during the constant pH simulation. We will then specify how λ is coupled to a temperature bath. After introducing the thermodynamic cycle that is used to couple the protonated and deprotonated states to the appropriate reference states, we will develop the constant pH MD method. Finally, we will generalize the λ-dynamics approach for multiple protonation sites in a protein.
2.1. Thermodynamic Integration
Thermodynamic integration (TI)(40) is used to calculate the free-energy difference (ΔG) between a reactant state R and a product state P:
Here, HTI is the Hamiltonian of the system, and λ is a coupling parameter that interpolates between the R (λ = 0) and P (λ = 1) states, e.g.,
To calculate ΔG via eq 1, λ is changed from 0 to 1 during the simulation, thus forcing the system from its reactant to its product state. The ensemble average in eq 1 is then taken from the MD ensemble generated from the Hamiltonian HTI(λ).
For later use, and following the notation of Kong and Brooks,(32) we split the Hamiltonians of the reactant and product in λ-dependent (H̃0 and H̃1) and λ-independent (HEnv) parts:
2.2. λ-Dynamics
In the λ-dynamics approach,(32) a Hamiltonian similar to eq 3 is used. In contrast to TI, λ is defined as an additional dynamic degree of freedom of the system with mass m, coordinate λ, and velocity λ̇. Accordingly, the Hamiltonian of the system is now expressed by(32)
with a force acting on λ,
where V(λ) is the potential energy part of the Hamiltonian in eq 4:
In eq 4, (m/2)λ̇2 is the kinetic energy term associated with the λ “particle”. The λ-dependent potential term U*(λ) will serve as a biasing potential to limit the range of λ; this will be defined further below.
2.3. Constraining the Interval of λ
Because only λ = 0 and λ = 1 represent physical states of the system−the protonated and deprotonated states−we require λ to be close to these values for most of the simulation time. More specifically, we require that:
-
(1)
the λ space is limited to the interval between the two physical states;
-
(2)
the average values of λ in the protonated and deprotonated states are close to 0 and 1, respectively;
-
(3)
the time spent at intermediate states by the system is short, i.e., the transitions between the protonated and deprotonated states are fast;
-
(4)
the residence time at the physical states is sufficiently long to allow conformational sampling of each state; and
-
(5)
the frequency of transitions can be controlled.
To address condition 1, a projection of an angular coordinate on the λ space has been proposed in previous applications.33,34,41 Here, we will extend this approach to meet also condition 2. Following Lee et al.,(34) we will address condition 3 by using a suitably chosen biasing potential. Finally, we will meet conditions 4 and 5 by adjusting the height of the biasing potential, taking into account the entropic part introduced by the use of the angular coordinate.
Note that a similar shape of the λ free-energy profile, which meets conditions 3 and 4, can be achieved also by designing ad hoc interpolation schemes between the potentials of the protonated and deprotonated states of λ, as previously proposed in the λ-adiabatic free-energy dynamics approach by Tuckerman and co-workers.(33) By adjusting the temperature of the λ particle, Tuckerman and co-workers,(33) ensured efficient barrier crossing, also meeting the last condition.
2.3.1. Projection of the Angular θ Coordinate on the λ Space
In order to constrain the space sampled by λ, we switch to a new dynamic angular coordinate θ, as shown in Figure 1. By this modification, the actual dynamics takes place in θ space, and λ is redefined as the projection of θ on the abscissa (see Figure 1),
The force acting on θ is
with V being the potential energy of the system, as defined in eq 6.
Figure 1.
(A) Schematic describing the angular coordinate. λ is defined as a function of the angular θ coordinate, λ = r cos(θ) + (1/2), with the radius of the circle being defined as r = (1/2) + σ, and σ a fluctuation size (see main text). The segments of circumference corresponding to the intervals a and b close to the end and center of the λ interval, respectively, are indicated. (B) Entropic free-energy term introduced by the use of an angular coordinate θ.
In contrast to previous approaches,33,34,41 where r = 1/2, and to meet condition 2, we chose r = (1/2) + σ, with an appropriate fluctuation size σ. Several values of σ were tested. We have used a value of σ = 0.05, because, with this value, the average λ at the physical states was ∼0 (protonated state) and ∼1 (deprotonated state).
2.3.2. Biasing Potential
To meet condition 3, a parabolic biasing potential of the form(34)
is used. By adjusting its height h, the frequency of the protonation transitions can be controlled, as required by condition 5.
Note that the choice of the above angular coordinate implies an entropic contribution to the effective free energy governing the λ-dynamics. This contribution originates from the higher density of λ states at the end points of the λ interval, with respect to the center of the interval, as indicated by the mapping of the intervals a and b in Figure 1A onto the circumference. The segment length for a given value of λ is
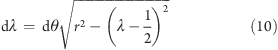 |
resulting in a free-energy contribution of
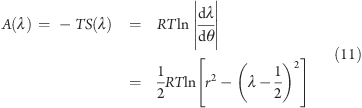 |
where R is the gas constant and T is the temperature. The A(λ) term in eq 11 stabilizes the end parts of the λ interval by a barrier of a few kJ mol–1, as shown in Figure 1B. This barrier needs to be taken into account when adjusting the height h of the biasing potential.
Note that the free energy A(λ) in Figure 1B, as well as the corresponding probability distribution, diverges for λ = 0 and λ = 1. This is, however, not a problem, because, for any finite interval [λ1···λ2], there is a finite probability for the system to be within this interval. Similarly, the partition function integral
with β = 1/(κBT), over every finite λ interval of the free-energy curve is also finite.
2.4. λ-Dynamics Thermostat
The temperature of the λ particle is kept constant by coupling the particle to an external heath bath. We have considered two coupling schemes, the Berendsen,(30) or weak coupling thermostat, and the Andersen thermostat.(42)
It is not clear a priori whether to couple the λ particle to (i) the same heat bath as the real atoms of the system, or (ii) a separate heat bath. In the first situation, the temperature is computed from the total kinetic energy of the real atoms and the λ particle. In the second, different heat baths are used to couple the λ particle and real atoms separately, and the kinetic energy of the λ particle is used to calculate the temperature of the λ subsystem.
Therefore, we have tested the two coupling schemes. For variant (i), we used the Berendsen thermostat (with a coupling time of 0.10 ps), whereas, for variant (ii), the λ particle was coupled to the Andersen thermostat (with a coupling time of 0.15 ps), and the rest of the system to the Berendsen thermostat. We have used the Andersen thermostat, because the Berendsen thermostat is not suitable for low-dimensional systems, such as the λ subsystem.(30) At 300 K and with a λ particle mass of 20 u, the latter coupling scheme generated λ-trajectories that were more suitable (i.e., sufficiently long residence time at the physical states, fast transitions) to simulate biomolecular systems (see the Results section).
2.5. Constant pH MD Simulations with λ-Dynamics
To describe protonation and deprotonation events of a titratable site at a given pH, we included, within the Hamiltonian in eq 4, (i) the effect of the external pH bath on protonation and (ii) contributions to the free energy of protonation due to breakage and formation of chemical bonds, which are not described by the force field. These two free-energy contributions will be described by an additional term Vchem(λ), which will shift the protonation equilibria by a certain free energy (ΔGchem).
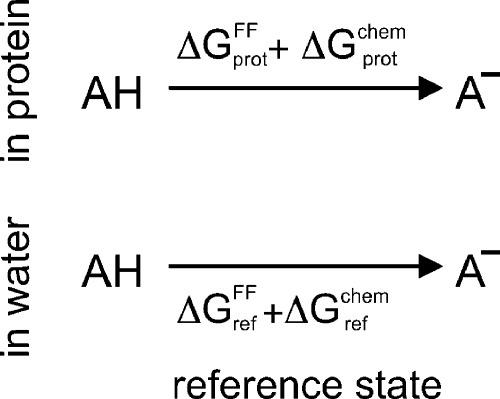
To determine ΔGchem, we considered the equilibrium between a protonated (AH) and a deprotonated acid (A−), in a (solvated) protein (see Figure 2, top) and in water (see Figure 2, bottom). We will use the latter as a reference state. This state is chosen such that a measured deprotonation free energy is available, and the reference compound AH is chemically similar for the reference and protein states, generally a solvated amino acid. Note that no H+ or H3O+ species appears on the right side of the equilibria in Figure 2, since, here, we consider the free-energy difference between the protonated and deprotonated forms of the titratable site. Below, we will describe how the pH dependency of this free energy is taken into account.
Figure 2.
Equilibria between the protonated (AH) and deprotonated (A–) forms of a titratable site in a protein and in the reference state in water. ΔGprotFF and ΔGref are obtained from a molecular dynamics (MD) simulation, whereas ΔGprotchem and ΔGref include contributions from the environmental pH and from bonded terms, which are missing in the force field. We assume ΔGprotchem ≈ ΔGref.
The free energies for the top (prot) and bottom (ref) reactions of Figure 2 are split into a contribution ΔGFF (obtained via a force field calculation) and ΔGchem (contributions (i) and (ii) from pH bath and bond breakage and formation, respectively). Because of the choice of the reference state, ΔGchem is not expected to differ significantly between the top and bottom reactions in Figure 2.18,43,44 Thus, the dominant contribution to the difference in the free energies of these two reactions is due to the different environment of the titratable site in the protein and in water. This contribution essentially depends on the long-range interactions of the titratable group, which are described by the force-field free-energy terms ΔGprotFF and ΔGref.
Accordingly,
where pKa,ref is the measured pKa of the reference titratable site in the reference state. The pH term describes the pH dependency of the equilibria in Figure 2, thus accounting for the missing proton in Figure 2.
The last contribution in eq 13, ΔGrefFF, is obtained from a thermodynamic integration calculation (reference free-energy simulation), which is performed prior to starting the constant pH simulation,
 |
where Href(λ) is the Hamiltonian of the reference system.
Having determined ΔGchem for the protein state, the following potential Vchem(λ) serves to implement the desired free-energy difference in the λ-dynamics calculations:
with ΔG̃refFF(λ) as a polynomial fit to Gref(λ), which is typically close to a parabola.45,46
Note the use of ΔG̃refFF(λ) to describe the ΔGref(λ) contribution, instead of a linear function of λ (analogously to the first term in eq 15). By this choice, the free-energy profile of the reference state (GrefFF(λ)) is effectively subtracted (except for fluctuations) from the one of the protein state (Gprot(λ)). In the simplest case of a constant pH simulation of an amino acid in water, in which case GrefFF(λ) and Gprot(λ) are the same, ΔG̃refFF(λ) will, therefore, remove the barrier in the energy landscape between the protonated and deprotonated states of the titratable site. Therefore, the barrier is given and controlled directly by the height of the biasing potential, which thus can be adjusted to achieve the desired transition rates. In the less trivial case of a protein simulation, ΔG̃ref(λ) will not remove the barrier completely, but still the remaining perturbation can be assumed to be small also in the general case.
2.5.1. Reference Thermodynamic Cycle
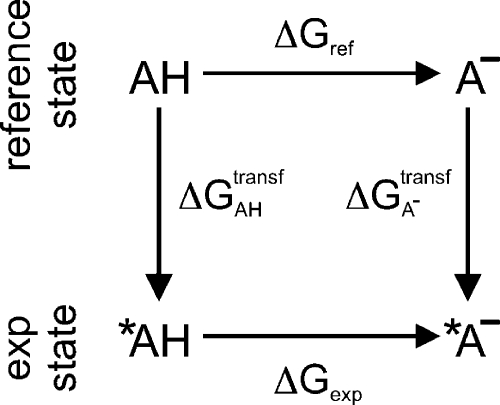
If a measured pKa is available only for a compound that is similar, but not identical, to that considered in the reference state, a thermodynamic cycle can be used to calculate and correct for the free-energy difference due to this modification. In Figure 3, the free-energy difference of the reference state (ΔGref) is given by
where ΔGAHtransf and ΔGA– indicate the free-energy differences for the transformation of the protonated and deprotonated forms of the reference state into the corresponding compounds of the experimentally known state (exp), respectively. The terms *AH and *A– in Figure 3 denote compounds chemically similar to those in the reference state.
Figure 3.
Thermodynamic cycle for the calculation of the reference free-energy difference ΔGref. AH and A– are transformed to chemically similar compounds *AH and *A–, respectively, for which the free-energy difference has been experimentally measured (ΔGexp).
After calculation of ΔGAHtransf and ΔGA– by conventional TI, these two free-energy differences are included in eq 4, similar to Vchem(λ) in eq 15:
This approach will be used further below to parametrize the λ-dynamics simulation of histidine.
2.6. Generalization to Multiple Titratable Groups
The above formulation of the λ-dynamics approach for constant pH simulations is extended to multiple titratable groups by assigning a separate λ-coordinate to each titratable group in the protein.34,35 In order to illustrate the approach, we first will consider the case of two titratable sites on a protein and derive the Hamiltonian for this system. We will then distinguish the case of two sites, which are (i) chemically uncoupled and (ii) chemically coupled. In the first case of uncoupled sites, interactions between titratable sites are mainly governed by electrostatics. In terms of the force field, these sites interact only via nonbonded interactions, which are described by the Coulomb and Lennard-Jones potential energies. For this reason, the Hamiltonian for uncoupled sites can be extended in a straightforward manner to any number N of uncoupled titratable sites in a protein,34,35 and formally linear scaling with the number of sites is achieved. As this approach will be used later on, we will review it below. For chemically coupled sites, this straightforward approach is not applicable. In this case, the chemical character, which is described in the force field by a set of parameters, such as atomic charges, bonds, and angles, of the titratable sites depends on the protonation states of the respective other coupled sites. Because of this dependency, cross terms occur in the expression for the potential energies, which have to be taken into account explicitly, and the contributions of interacting atoms cannot be rearranged as conveniently as those for uncoupled sites. Therefore, unavoidably, in this case, the number of calculations scales exponentially with the number of sites, rather than linearly. Here, we will discuss the example of histidine, where the two deprotonation sites on the side chain are chemically coupled. Note that, in this case, since only two sites are coupled, the calculations still scale linearly. We will also discuss how this description of histidine differs from the treatment of Khandogin and Brooks.(35)
2.6.1. Constant pH λ-Dynamics of Two Titratable Sites on a Protein
We start by considering the case of two titratable sites on a protein. Each of the two sites i and j is described by a λ-coordinate, λi and λj, respectively. At λ = 0, the site is protonated; at λ = 1, the site is deprotonated. Independent of whether the two titratable groups are uncoupled or coupled, four protonation states are relevant. In Figure 4, these four states for histidine are denoted as 00 (both sites i and j protonated), 10 (site i deprotonated and site j protonated), 01 (site i protonated and site j deprotonated), and 11 (both sites i and j deprotonated).
Figure 4.
Four protonation states of the histidine side chain: λ1 and λ2 are the titration coordinates of the Nε and Nδ deprotonation sites, respectively. λ1 = λ2 = 0 (00) corresponds to the fully protonated and positively charged histidine; λ1 = 0, λ2 = 1 (01) and λ1 = 1, λ2 = 0 (10) correspond to the neutral histidine; and λ1 = λ2 = 1 (11) corresponds to the negatively charged fully deprotonated histidine.
Applying eq 4 in a first step to each group i and j separately, and combining the two resulting Hamiltonians again, according to eq 4 in a second step, yields
 |
where the first four Hamiltonians on the right side of the equation describe the titratable sites of the protein in the four protonation states in Figure 4, and U*(λ) is the biasing potential discussed earlier in section .
Similarly, the potential energy of the system described by the Hamiltonian H(λi,λj) in eq 18 is given as
 |
where the first four potential energies V on the right side of the equation describe the interactions of the titratable sites in their respective states (see Figure 4), with forces acting on λi and λj, respectively:
 |
and
 |
As can be seen for the case of two interacting titratable sites, the force acting on each site depends on the protonation state of the respective other site, which also holds true for the general case of N interacting sites. This interdependence entails an exponential scaling.
2.6.2. Chemically Uncoupled Titratable Sites
If the two titratable sites are chemically uncoupled, however, the computational complexity is dramatically reduced. Uncoupled sites interact only via long-range (nonbonded) interactions. Below, we will show how these interactions (Coulombic and van der Waals) are efficiently described, achieving linear scaling of the calculations.
Coulombic Interactions
For two uncoupled titratable sites i and j, the Coulombic potential energy (Vc) for two interacting atoms simplifies (from eq 19) to
where q0 and q1 are the atomic charges in the protonated (λ = 0) and deprotonated (λ = 1) states, respectively, of the corresponding atoms, r is the distance between the two atoms, and ϵ is the permittivity. Note that eq 22 involves only two states, compared to the four states of eq 19.
Accordingly, the force acting on λi is
where the Coulombic energies Vc(λi = 0, λj) = [1/(4πϵ)]q0i[(1 – λj)q0 + λjq1j] and Vc(λi = 1, λj) = [1/(4πϵ)]q1[(1 – λj)q0j + λjq1] are evaluated at λj.
Equation 23 is extended in a straightforward manner to N uncoupled interacting sites:
 |
and linear scaling of the calculation with the number of interacting uncoupled sites is achieved.
van der Waals Interactions
The remaining long-range interactions are somewhat less straightforward. We consider the usual case where the van der Waals energies, together with the Pauli repulsion, are described by a Lennard-Jones potential VLJ:
where r is the distance between the two atoms, and A and B are two parameters, which depend on the pairs of interacting atoms i and j,
and similarly for B.
For two uncoupled titratable sites i and j, the Lennard-Jones potential energy for two interacting atoms is (here, we treat only the r12 part; the r6 part is very similar)
 |
where the indices of the A parameter indicate the protonation states of the two titratable sites (see Figure 4).
Similar to the Coulombic energy, eq 27 is rearranged in terms of the protonated (λ = 0) and deprotonated (λ = 1) values of the Ai and Aj Lennard-Jones parameters,
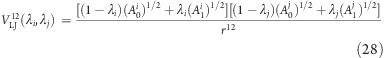 |
with force acting on λi
The potentials VLJ12(λi = 1, λj) and VLJ(λi = 0, λj) are obtained by evaluating the second term in square brackets on the right side of eq 28 prior to starting the force calculation, analogous to the calculation of the Coulombic forces. As a more technical remark, note that, in GROMACS,(39) the Lennard-Jones parameters are not accessible in a straightforward manner in the MD source code. Therefore, instead of interpolating linearly between (A0j)1/2 and (A1j)1/2, we define the atom type (a) of the j atom, which is used to determine A0j and A1j, prior to calculating the force, by
 |
This yields, effectively, an approximation to the second term in square brackets on the right side of eq 28. Note that, in the GROMOS96 force field,(47) only the A term of the atoms of the carboxylic group changes upon deprotonation. Since, in the Lennard-Jones potential (eq 25), the A (the repulsion) term decays with 1/r12, the approximation in eq 30 is not expected to introduce significant artifacts.
2.6.3. Chemically Coupled Titratable Sites
We move now to the situation of chemically coupled sites. To illustrate this case, Figure 4 shows the four protonation states of histidine, where λ1 and λ2 denote the titration coordinates of the Nε and Nδ sites, respectively. In contrast to the chemically uncoupled situation, here, the protonation state of one site (e.g., Nδ) does affect the charge of the other site (Nϵ). Depending on the chemistry, other force-field parameters also may be affected. This prevents further simplification of eq 18, which leaves us with four Hamiltonians (H̃00, H̃01, H̃10, and H̃11) and four states for the atomic charges (q00, q01, q10, and q11). Therefore, the calculations will scale exponentially with the number of coupled sites, as each combination of the protonation states of the sites must be evaluated.
We note that this description of histidine differs from that of Khandogin and Brooks,(35) in that each of the two titratable sites on the side chain is described by a titration coordinate, and the coupling between the two sites is taken into account explicitly. Accordingly, our treatment also describes the doubly deprotonated, negatively charged form of histidine, which is not included in the model of Khandogin and Brooks,(35) where only three states are considered. Furthermore, our treatment is readily generalized to more than two chemically coupled titratable sites.
Chemically Coupled Reference States
The chemical coupling between titratable sites also must be taken into account for the reference states in a constant pH simulation. For example, when λ2 changes from 0 to 1 in histidine, the reference deprotonation reaction of the titratable site described by λ1 changes from the bottom (00 ⇋ 10) to the top (01 ⇋ 11) deprotonation equilibrium in Figure 4.
To account for this dependency, we define Vchem(λ1, λ2) (see for comparison Vchem(λ) in eq 15), e.g., for group λ1, as
where
and ΔG̃refFF(λ1, λ2) is a polynomial fit to Gref(λ1, λ2), which is the force-field free-energy profile for the reference deprotonations. To determine ΔG̃refFF(λ1, λ2), several reference free-energy simulations at different values of λ2 are performed (see the Methods section).
Similarly to the reference state, the reference thermodynamic cycle (in section ) of chemically coupled titratable sites will depend on the protonation state of the respective other sites. For the example of histidine, eq 17 becomes, e.g., for group λ1,
with ΔGAHH+, ΔGAH, and ΔGA– being the transfer free energies of the double protonated (00), singly protonated (10 or 01), and fully deprotonated (11) forms of histidine (see Figure 4).
3. Methods
3.1. pKa Calculations
To estimate the pKa of a titratable compound, constant pH simulations of the compound at different pH values were performed, similar to a titration experiment. From each simulation, the fraction (S) of deprotonated acid was calculated, and the Henderson–Hasselbalch equation was fitted to the obtained titration curve,
which, for N noninteracting titratable sites, takes the form
In one case, where the fit was not satisfactory, the Hill equation has been used,
where n is the Hill coefficient, which accounts for the degree of cooperativity (n > 1) or anticooperativity (n < 1) of the system.48,49
The fraction of deprotonated acid S in a constant pH simulation was calculated from the titration coordinate λ during the simulation, where all steps with λ < 0.1 were recorded as protonated and those with λ > 0.9 as deprotonated. The error in the calculated S was estimated via a Bayesian approach from the number of transitions observed during the simulations between the protonated and deprotonated states (see the Supporting Information).
In contrast to a conventional titration experiment, in a constant pH simulation, the titration coordinates of each titratable site in the compound are accessible. Therefore, both the macroscopic (or apparent) pKa values of the entire compound, and the microscopic pKa values of each site, can be estimated.
For a compound with two titratable sites, such as histidine, the equilibrium constant for the deprotonation of the first proton (Ka,I) is related to the equilibrium constants for the deprotonations at sites Nϵ and Nδ (Ka,1′ and Ka,2, respectively) by
from which follows
with pKa,I the (macroscopic) pKa value for the deprotonation of the first proton of histidine, and pKa,1′ and pKa,2 the (microscopic) pKa value for the deprotonation of the first proton of histidine at sites Nϵ and Nδ, respectively.
Similarly, the equilibrium constant for the deprotonation of the second proton of histidine (Ka,II) is related to the equilibrium constants for the deprotonations at sites Nϵ and Nδ (Ka,1′′ and Ka,2, respectively) by
 |
from which follows
where pKa,II is the second macroscopic pKa value of histidine, and pKa,1′′ and pKa,2 the microscopic pKa values for the deprotonation of the second proton at sites Nϵ and Nδ, respectively.
In all cases, the error in the calculated pKa has been determined from the standard deviation of a set of four or five pKa obtained from different fragments of the simulations.
3.2. Constant pH MD Simulations
The constant pH MD simulation method, as described above, was implemented in the GROMACS MD package (version 3.3).37−39
As test cases, constant pH simulations were carried out for four compounds: glutamic acid (Glu) with neutral termini, a dipeptide of sequence glutamic acid-alanine (Glu-Ala), imidazole, and a capped histidine (acetyl-NH-CHR-CO-methylamide with R the side chain of histidine). Glu, Glu-Ala, and histidine (His) were described with the GROMOS96 53A6 force field.(50) Force-field parameters of imidazole were adapted from histidine (atomic charges are listed in Table s1 in the Supporting Information). For the fully deprotonated form of histidine, no force-field parameters are available in GROMOS96.(50) Charges for this protonation state were thus taken from imidazole and, therefore, are not very accurate. However, in the pH interval considered here (pH 4–10), the doubly deprotonated state should never be visited, because the pKa value for the second deprotonation of histidine is far beyond than the pH interval.(1) Thus, we do not expect a large influence of the charges on the protonation populations.
Each compound was placed in a dodecahedral box, which was subsequently filled with ∼4200–5200 SPC (simple point charge) water molecules.(52) Interactions between atoms within 1.0 nm were evaluated at every step of the simulation, while interactions with atoms beyond 1.0 nm were evaluated every five steps. The Lennard-Jones long-range cutoff was set to 1.6 nm. The Particle Mesh Ewald (PME)54,55 was used for the long-range electrostatic interactions, with a grid spacing of 0.12 nm and an interpolation order of 4. Constant pressure and temperature were maintained by weakly coupling the system to an external bath at 1 bar and 300 K, using the Berendsen barostat and thermostat(30) with coupling times of 1.0 and 0.1 ps, respectively. A leapfrog integrator was used with an integration time step of 2 fs. The bond distances and bond angles of water were constrained using the SETTLE algorithm.(56) All other bond distances were constrained using the LINCS algorithm.(57) Prior to the simulations, the potential energy of each system was minimized using a steepest descent approach. A 50-ps MD simulation with position restraints (with a force constant of 1000 kJ mol–1 nm–2) on the amino acid/peptide atoms was then performed to relax the water molecules. Finally, a 5-ns simulation was performed to equilibrate each system before starting the constant pH MD simulations.
Deprotonation of a site was achieved by transforming the titratable hydrogen into a dummy atom, which is topologically bound to the acid, but has no interactions with the rest of the system. Charges and atom types of the ionizable groups were changed accordingly, from their force-field values in the protonated state (λ = 0) to the deprotonated state (λ = 1). Bonded terms (bonds, angles, and torsions) were maintained in the protonated state. For glutamic acid and C-terminal, this effectively yields an approximate description of the deprotonated state. For N-terminal, imidazole, and histidine, instead, the bonded terms do not differ in the protonated and deprotonated states of the GROMOS96(50) force field. For glutamic acid in explicit solvent, the free energy of deprotonation was calculated, as described in the next section for the reference free-energy simulations, with and without change in the bonded terms. The difference was less than 2 kJ mol–1 (see Table s2 in the Supporting Information).
To compare constant pH simulations performed with two different force fields, the titration curve of Glu with neutral termini was calculated also with OPLSA(51) and TIP4P(53) water molecules, and the titration curves for a tripeptide Ala-Glu-Ala were calculated with GROMOS96(50) and OPLSA(53) in SPC(52) water. When OPLSA(53) was used to describe the system, in addition to the bonded terms, atom types also were mantained in their protonated state.
The temperature of the λ degree of freedom was set to 300 K. Unless indicated otherwise, each λ particle was coupled to a separate heat bath via the Andersen thermostat(42) with a coupling parameter of 6 ps–1. A fixed barrier height of 3.0 kJ mol–1 was used for the biasing potential.
The mass of λ was set to 20 u. With this value of the mass, the calculations yielded suitable λ-trajectories (i.e., small ratio between transition time and residence time) for the simulated systems (see the Results section). At the same time, the mass of λ is in the same range as that for the other atoms in the system.
Finally, we note that during the change of the protonation state in the constant pH simulations, the overall charge of the system is (eventually) changed. In this situation, artifacts can arise due to the use of Ewald and related methods to describe electrostatic interactions. In particular, these artifacts are related to the periodic boundary conditions and the background charge that is used to neutralize the system.58,59 However, for small compounds in a high dielectric medium (water), such as those investigated here, these effects are expected to be negligible.28,58
3.3. Reference States and Reference Free-Energy Simulations
Constant pH simulations require a reference state for each of the simulated titratable sites. The measured and calculated (force field) deprotonation free energies of this reference state were used to include the effect of the pH bath, and the effect of the breakage and formation of chemical bonds in the simulation (see eq 13).
Table 1 lists the titratable sites and their reference states, as well as the measured pKa values obtained from the literature1,60−62 and force-field deprotonation free energies (ΔGrefFF). Note that two measured pKa values and ΔGref are reported for imidazole. These correspond to the microscopic pKa values for the first and second deprotonation reaction of imidazole, respectively (the second microscopic pKa value is obtained using eq 40, with the second macroscopic pKa value being approximated from histidine, for which there are experimental data(1)). The first and second microscopic pKa values of the Nδ and Nϵ sites are identical, because of the symmetry of the imidazole molecule.
Table 1. Reference States, Reference pKa Values, and ΔGrefFF Values.
| titratable site | reference state | reference pKa | (ln 10)RT (pKa,ref) (kJ mol–1) | ΔGrefFF (kJ mol–1) |
|---|---|---|---|---|
| Glu | Glu (neutral termini) | 4.25(60) | 24.4 | –220.8 |
| N-terminus | di-Ala (neutral C-terminus) | 8.0(61) | 45.9 | 332.8 |
| C-terminus | di-Ala (neutral N-terminus) | 3.5(61) | 20.1 | –231.3 |
| imidazole (Nδ)a | imidazole (Nδ) | 7.28,(62) 14.4(1) | 41.8, 82.7 | 155.4, −211.7 |
For imidazole, only Nδ is reported ; values for Nϵ are the same.
For the Ala-Glu-Ala tripeptide, which was added to the compounds set to compare the GROMOS96(50) and OPLSA(53) force fields, the reference states were chosen as follows: acetyl-Glu-methylamide (pKa,ref = 4.25,(60) ΔGrefFF(GROMOS) = – 225.6 kJ mol–1, ΔGref = – 370.5 kJ mol–1), di-Ala-methylamide (pKa,ref = 8.0,(61) ΔGrefFF(GROMOS) = 331.7 kJ mol–1, ΔGref = 219.0 J mol–1), and acetyl-di-Ala (pKa,ref = 3.5,(61) ΔGrefFF(GROMOS) = −230.7 kJ mol–1, ΔGref = −338.2 kJ mol–1), for titratable sites Glu, N-terminus, and C-terminus, respectively.
The force-field deprotonation free energies for the reference states ΔGrefFF were determined via conventional thermodynamic integration (see eq 14) as follows. Each reference compound was placed in a dodecahedral box filled with SPC(52) water molecules. The reference free-energy simulations consisted of 5-ns MD, during which λ was continuously increased from 0 to 1, thus deprotonating the reference compound, as described above for the constant pH simulations. The size and shape of the box in the reference and constant pH simulations was identical. Using the same simulation conditions in the reference and constant pH simulations, differences due to approximations of the force field and of the interaction potentials are minimized.(28)
ΔG̃refFF(λ) (eq 15) was derived from a least-squares fit to ∂H/∂λ obtained from the reference free-energy simulation. Since the deprotonation reaction in explicit water showed a nonlinear ∂H/∂λ profile,(28) a third-order polynomial was used. Coefficients of these polynomials are given in Table s3 in the Supporting Information.
The two titration coordinates λ1 and λ2 of imidazole (Figure 4) are chemically coupled and, therefore, deserved particular attention. Here, the reference state changes as a function of the protonation state of the respective other site. Thus, ΔGrefFF(λ1, λ2), and, accordingly, ΔG̃ref(λ1, λ2), are a function of both, λ1 and λ2 (see eq 31). For this reason, reference free-energy simulations of one titratable site (e.g., the site described by λ1) were carried out for λ2 = 0, 0.1, ..., 0.9, 1. For each of these 11 simulations, a third-order polynomial in λ1 was fitted to its ∂H/∂λ1 profile, in a manner similar to the case of chemically uncoupled sites. To describe the dependency from λ2, third-order polynomials in λ2 were subsequently fitted to the coefficients of these polynomials, and vice versa for the titratable site described by λ2. These two sets of polynomials served to calculate continuous forces for the two degrees of freedom λ1 and λ2.
3.3.1. Histidine Reference State
As the reference state for the constant pH simulations of histidine, we chose imidazole, such that contributions from the backbone to the proton affinities of the side chain Nϵ and Nδ titratable sites were present in the constant pH simulations, but not in the reference free-energy simulations. Because the force-field parameters of imidazole and histidine differed, imidazole was transformed to a modified imidazole molecule described with histidine force-field parameters, using the thermodynamic cycle in Figure 3. The transfer free energies along the thermodynamic cycle were then used to redefine the reference state, according to eq 16. Since Nϵ and Nδ are chemically coupled, the transfer potential Vtransf(λ1, λ2) was defined according to eq 33, which accounts for the dependency of the transfer free energies from the protonation state of the respective other site. The transfer free energies were calculated via free-energy simulations (thermodynamic integration, eq 1). In a first step, the bond lengths and angles were changed from their force-field values in imidazole to those in histidine. In a second step, Lennard-Jones parameters, and, in a last step, charges (see Table 1s in the Supporting Information) were modified. Each free-energy simulation consisted of 18 independent simulations with λ values between 0 and 1. At each λ value, 100 ps of equilibration were followed by 300 ps of data collection. The integration was carried out numerically using the trapezoidal method. The error in ⟨∂H/∂λ⟩λ was estimated using block averaging.63,64
3.4. λ Probability Distribution and Free-Energy Profile
In order to calculate the probability distribution p(λ) during the constant pH simulation, the λ interval was divided in 10 bins [λ1, .., λi, ..., λ10], and p(λ) at bin i was obtained as
where ni is the time of the simulation during which λ visited bin i and N is the total simulation time.
The probability distribution of λ, which is given by the entropic term introduced by the use of the circular coordinate, was calculated as
with
and A(λ) and Z being obtained from eqs 11 and 12, respectively. p(λi) was then used to obtain a free-energy profile as a function of the λ titration coordinate, with the free energy G(λ) at bin i being given by
4. Results
To test the accuracy of the constant pH MD simulation method described above, we have calculated the titration curves of four compounds: glutamic acid, a Glu-Ala dipeptide, imidazole, and histidine. The effects of the choice of the barrier height of the biasing potential, the temperature coupling scheme, and the force field, on the simulation were also investigated.
4.1. Glutamic Acid
First, we asked if the constant pH MD simulation method is able to accurately reproduce the titration curve of glutamic acid. To this end, glutamic acid with neutral amino and carboxyl termini (−NH2 and −COOH, respectively) was solvated in water, and four constant pH simulations of 5 ns each (0.5-ns equilibration time and 4.5-ns data collection time) were carried out for 11 pH values between 1.0 and 7.0. Figure 5 shows the fractions of deprotonated acid (in equivalents) as a function of pH (i.e., the titration curve) for each of the four sets of simulations (colored dots), and their average (black dots), the latter together with error bars, which were determined from the statistics of the observed transitions, as described in the Methods section and the Supporting Information. As can be seen, the scatter of the four simulations agrees with the error estimate of the average. Note that, at the end points of the titration curve, values slightly below 0 or above 1 are observed, which is due to the use of a radius of r = 0.55 for the circle covered by the angular coordinate θ (see the Theory section). We chose r = 0.55 to get 0 and 1, on average, at the protonated (λ < 0.1) and deprotonated states (λ > 0.9), respectively. Because of statistical fluctuations, however, slightly negative values and values above 1 occur. However, this is much better than averages of ⟨λ⟩ = 0.05 or ⟨λ⟩ = 0.95 for r = 0.5.
Figure 5.

Calculated titration curve of glutamic acid with neutral termini. The deprotonation of glutamic acid (in equivalents, eq) is plotted as a function of pH. At each pH, four simulations of 4.5 ns each were performed. Data from each of these simulations (colored dots), and from the average of the four simulations (black filled dots), are shown. Error bars denote estimates from the statistics of the observed transitions. The dashed line is a Henderson–Hasselbalch fit to the average data.
From a fit of the Henderson–Hasselbalch equation (eq 34) to the average deprotonation (the dashed line in Figure 5), the pKa value was estimated to be 4.21 ± 0.14, which is consistent with the measured pKa value of 4.25.(60)
For the chemists, we note that, in a titration experiment, the pH is usually measured as a function of the volume of a strong base (or acid) solution added to the analyte solution. In contrast, in the constant pH simulations, pH is a fixed parameter, whereas the equivalents of analyte (i.e., how much of the analyte supplies or reacts with one mole of hydrogen ions) is the quantity to be estimated. Therefore, the titration curves in Figure 5 are to be read as inverted titration curves, with respect to a typical experimental titration curve.
Figures 6A–C illustrate the effect of different barrier heights of the biasing potential (see eq 9). As expected, an increase of the barrier height by 1 kBT (∼ 2.5 kJ mol–1) reduces the number of transitions by a factor of ∼2.5–3. Therefore, by adjusting the biasing potential, the transition rate can be optimized to ensure sufficient sampling of the physical end states. At the same time, the fraction of intermediate states remains small (between 30% with a barrier of 3 kJ mol–1, and 10% with a barrier of 7.5 kJ mol–1). Overall, by adjusting the barrier, the statistical error of the constant pH simulation can be minimized.
Figure 6.
Dynamics of the deprotonation variable λ of glutamic acid for different barrier heights of the biasing potential and different temperature coupling schemes of λ: (A, B, C) λ is plotted over time during constant pH simulations at pH 4.25 for three different barrier heights ((A) 3.0 kJ mol–1, (B) 5.0 kJ mol–1, and (C) 7.5 kJ mol–1) of the biasing potential using the Andersen temperature coupling scheme. (D) In the left-hand side of the panel, λ is shown during a constant pH simulation at pH 4.25 for a barrier height of 3.0 kJ mol–1, using Berendsen temperature coupling; on the right-hand side of the panel, the λ-distributions of this simulation and of simulation (see panel A) are superimposed. (E) Variable λ and respective velocity vθ (in radians/ps) during 50 ps of simulation with Andersen and Berendsen temperature coupling schemes. (F) Distributions of the angular distances (in radians) covered between velocity reversals by the θ-variable, during the simulations depicted in panels A and D.
Note that the effective barrier between the protonated and deprotonated states has a contribution from the entropic barrier introduced by the use of an angular coordinate to perform the actual λ-dynamics (see the Theory section, Figure 1 and eq 11). This can be seen in Figure 7, which shows the free-energy profile as a function of the titration coordinate λ from an 18-ns constant pH simulation of glutamic acid in explicit solvent at pH 4.25 and with the barrier height of the biasing potential 3 kJ mol–1 (continuous line). The free energy at λ = 0.5 is ∼7 kJ mol–1 more positive than that at λ = 0 and λ = 1. When the biasing potential is subtracted from the simulation free-energy profile, we obtain the dotted line in Figure 1, which shows a residual barrier of ∼4 kJ mol–1. This compares with the entropic barrier term introduced by the use of the angular coordinate θ (broken dotted line in Figure 7).
Figure 7.
Relative free-energy profile as a function of the titration coordinate λ from the 18-ns constant pH MD simulation of glutamic acid in explicit solvent at pH 4.25 (continuous line). The biasing barrier potential (barrier height = 3 kJ mol–1) is subtracted from the simulation free-energy profile to yield the dotted line. The broken dotted line is the relative free-energy profile that is due to the circle entropy (−TS(λ); see text).
To investigate the effect of the chosen temperature coupling scheme on sampling of the protonation states during the constant pH simulations, the following two variants were considered. In variant (i), the λ particle was coupled to a separate heat bath via the Andersen thermostat,(42) and the rest of the system was coupled to the Berendsen thermostat, whereas in variant (ii), all degrees of freedom were coupled to a common heat bath via the Berendsen thermostat.(30) Figures 6A and 6D compare typical λ-trajectories for the two variants. As can be seen, the number of transitions for the Berendsen variant is ∼3–4 times larger than that for the Andersen method. Accordingly, the average residence time is ∼3–4 times shorter for the Berendsen simulation (∼60 ps), compared to that for the Andersen simulation (∼200 ps). The probability distributions of λ with the two variants of the temperature coupling scheme are very similar (see right plot of Figure 6D). Figure 6E shows typical short-time (50 ps) traces of both simulations, with λ(t) shown in the top row, and respective velocities of the underlying angular coordinate (vθ) at the bottom. As can be seen, the λ-trajectories are similar, with the Berendsen variant showing somewhat larger oscillations at the end states. The velocities, in contrast, look very different, with a marked proportion of high-frequency fluctuations for the Andersen thermostat, which are absent for the Berendsen thermostat. Figure 6F quantifies this behavior, in terms of the distribution of angular distances covered by the circular coordinate θ between successive velocity reversals. These distances are, on average, shorter for the Andersen thermostat (0.08 radians), as compared to the Berendsen thermostat (0.57 radians). In particular, the long tail for the Berendsen thermostat (up to 6 radians) shows that inertia-driven full circle motions do occur, which implies correlated transitions. This effect reduces the statistical accuracy and is not seen for the Andersen thermostat.
Overall, the Andersen temperature coupling scheme seems to provide a better tradeoff between residence times and the number of uncorrelated transitions. In particular, the λ-trajectories obtained with the Andersen variant showed a sufficiently long residence time at the physical end states, allowing the system to respond to the new protonation state. Because these features are crucial for constant pH simulations, the Andersen temperature coupling scheme has been used for all subsequent simulations.
4.2. Glu-Ala Dipeptide
The second system that we considered was the dipeptide Glu-Ala. This system has three interacting titratable sites—glutamic acid (Glu), amino terminus (N-terminus), and carboxyl terminus (C-terminus)—and, therefore, was chosen to test if our method is capable of describing pKa shifts due to these interactions.
Constant pH simulations were carried out for 14 pH values between 1.0 and 11.0. Each trajectory covered a 20-ns simulation time with a 2-ns equilibration time and an 18-ns data collection time. Figure 8 shows the obtained titration curve (left graph), in which the cumulative deprotonation (in equivalents) of all three titratable sites is plotted as a function of pH, together with the individual contributions of the three sites (see right side of Figure 8).
Figure 8.
Calculated titration curves of a Glu-Ala dipeptide: (left) titration curve of the dipeptide and (right) site-specific titration curves of the N-terminus, Glu, and C-terminus. The fitted Henderson–Hasselbalch curve (dashed line) and, for the C-terminus, the fitted Hill curve (dashed magenta line) are also shown. Error bars denote estimates from the statistics of the observed transitions.
Apparent pKa values were estimated from a fit of a sum of three Henderson–Hasselbalch equations (eq 35) to the cumulative titration curve (Table 2). Similarly, the pKa values of each of the titratable sites (site-specific pKa values) were obtained by fitting the Henderson–Hasselbalch equation to the individual titration curves (see Table 2). Note that the apparent pKa values are listed in Table 2, next to each titratable site, only for the sake of clarity, because they are defined in terms of deprotonation of the entire dipeptide.
Table 2. Calculated pKa values of the Glu-Ala di-peptide .
| titratable site | apparent pKa | site-specific pKa | reference pKaa |
|---|---|---|---|
| N-terminus | 8.66 ± 0.13 | 8.79 ± 0.10 | 8.0(61) |
| Glu | 3.33 ± 0.08 | 3.05 ± 0.08 | 4.25(60) |
| C-terminus | 2.76 ± 0.07 | 2.98 ± 0.07 | 3.5(61) |
Measured pKa values of the isolated titratable sites (reference pKa values) are listed for the sake of comparison.
The apparent and site-specific pKa values are similar for the N-terminus, whereas, for Glu and for the C-terminus, there is a difference of 0.28 and −0.22 pKa units, respectively (see Table 2). The Henderson–Hasselbalch curve fitted the calculated deprotonation equivalents of the N-terminus and Glu (see top and center right of Figure 8) well, whereas the titration curve of the C-terminus (see bottom right of Figure 8) deviated slightly from the Henderson–Hasselbalch curve. In particular, the slope of the titration curve is shallower, as is indicative of interactions between titratable sites.48,49 Since the N-terminus was constantly protonated below pH 7 (see top right in Figure 8), the interacting titratable sites were the C-terminus and Glu, which had similar pKa values (∼3). A fit of the Hill equation (eq 36) to the C-terminus titration curve (dashed magenta line in Figure 8, lower graph) recovers the pKa value of 2.98 already obtained for the Henderson–Hasselbalch fit, and it provides a better description of the titration behavior. The obtained Hill coefficient of n = 0.82 indicates a certain degree of anticooperativity in the binding/unbinding of the proton. This is expected, as both the deprotonated C-terminus and Glu are negatively charged, and the release of a proton from one site will increase the affinity of the respective other site.
To quantify the interaction between the C-terminus and Glu in terms of a free energy, we determined the shift in the pKa values of these two groups, which is due to the change in the protonation state of the respective other group. For that purpose, we selected, for each titratable site from the trajectories, those frames where the respective other site (C-terminus or Glu) was protonated or deprotonated. In the former case (trajectories where the opposite site was always protonated), we obtained the titration curve for the deprotonation of a site given the respective other was protonated (first microscopic titration curve), whereas in the latter (trajectories where the opposite site was always deprotonated), we obtained the titration curve given the other site was deprotonated (second microscopic titration curve). From a fit of the Henderson–Hasselbalch equation to the first and second microscopic titration curves, we obtained the microscopic pKa values (pKa′ and pKa″, respectively). For the C-terminus, pKa′ = 2.89 and pKa″ = 3.05, and for Glu, pKa′ = 2.95 and pKa′′ = 3.11, which show a difference of 0.16 pKa units between the first and second microscopic pKa values for both the C-terminus and the Glu. Thus, the affinity of the two titratable sites for the proton increased upon deprotonation of the other site by ∼1 kJ mol–1, which is of the same order as a simple estimate of the interaction energy (at the average distance of 0.6 nm, see below) from the Coulombic law (∼3 kJ mol–1).
As the C-terminus and Glu became charged, the average distance between these two groups increased. In particular, this distance changed gradually from 0.55 nm to 0.60 nm between pH 1 (when both groups were protonated) and pH 6 (when both groups were negatively charged), and then more markedly from 0.60 to 0.74 nm between pH 8 and pH 11, when the N-terminus was mostly deprotonated, and the system had a net charge of −2.
As can be seen from Table 2 when comparing the site-specific and reference pKa values, in all three cases, a shift in the pKa value was observed, favoring the charged form of the titratable sites in the dipeptide. In particular, the pKa of the N-terminus increased by almost 1 pKa unit, whereas the pKa of the Glu and C-terminus decreased by 1.2 and 0.5 pKa units, respectively. The more-pronounced shifts in the pKa value of the N-terminus and Glu suggest that these two groups interact favorably in their charged states. The average distance between the nitrogen of the N-terminus and the oxygens of the carboxyl group of Glu decreased from 0.47 nm to 0.43 nm between pH 2 and pH 6 and, beyond pH 8, increased again to 0.47 nm. The N-terminus and Glu were at the closest distance of 0.43 nm between pH 6 and pH 8, when both groups were mainly in their charged states. No significant salt-bridge formation was observed between these two groups (<15% of simulation time). On average, the distance between the C-terminus and N-terminus was larger, and almost constant, between pH 1 and pH 8 (between 0.58 nm and 0.59 nm).
4.3. Force-Field Comparison: GROMOS96 and OPLSA
To assess the sensitivity of the constant pH MD approach to the chosen force field, we calculated the titration curve and pKa value of glutamic acid (with neutral termini) with a second force field. In particular, the OPLSA(51) and TIP4P(53) explicit water model was used. In addition, we calculated titration curves and pKa values for a tripeptide of sequence Ala-Glu-Ala with GROMOS96(50) and OPLSA,(51) both with an SPC(52) explicit water model.
For glutamic acid with neutral termini, both force fields yielded very similar titration curves, with pKa values very close to the reference pKa value, as can be seen in Table 3 and in Figure s1 in the Supporting Information. This is expected, because the constant pH simulation is parametrized via the measured pKa value of the reference state, which, in these simulations, was glutamic acid, such that any possible force-field bias should cancel.
Table 3. Calculated pKa Values of a Single Glutamic Amino Acid with Neutral Termini (NH2-Glu-COOH), and Ala-Glu-Ala Tripeptide with GROMOS96(50) and OPLSA,(51) in Combination with TIP4P(53) and SPC(52) Water Molecules.
|
NH2-Glu-COOH | |||
|---|---|---|---|
| GROMOS96 + SPC | OPLSA + TIP4P | ||
| titratable site | pKa | pKa | reference pKaa |
| Glu | 4.21 ± 0.14 | 4.14 ± 0.07 | 4.25(60) |
|
Ala-Glu-Ala | |||||
|---|---|---|---|---|---|
| GROMOS96 + SPC |
OPLSA + SPC |
||||
| titratable site | apparent pKa | site-specific pKa | apparent pKa | site-specific pKa | reference pKaa |
| N-terminus | 7.93 ± 0.08 | 8.05 ± 0.08 | 8.01 ± 0.10 | 8.15 ± 0.09 | 8.0(61) |
| Glu | 4.48 ± 0.13 | 4.46 ± 0.07 | 4.09 ± 0.18 | 4.04 ± 0.06 | 4.25(60) |
| C-terminus | 3.14 ± 0.12 | 3.12 ± 0.11 | 3.55 ± 0.18 | 3.59 ± 0.07 | 3.5(61) |
Measured pKa values of the isolated titratable sites (reference pKa values) are listed for the sake of comparison.
For the Ala-Glu-Ala tripeptide, at each of 15 pH values between 1 and 11, four constant pH simulations were performed for a total of 30 ns per pH value. Slight differences between the titration curves obtained with the two force fields are seen. In particular, the Glu and C-terminus titration curves differed most significantly (see Figure s2 in the Supporting Information). As can be seen in Table 3, the site-specific pKa of the C-terminus is shifted by −0.4 pKa units, with respect to the reference pKa value in the GROMOS96 simulations, whereas it is shifted slightly by 0.1 pKa unit in the OPLSA simulations. For Glu, the site-specific pKa value is shifted by 0.2, with respect to the reference state, in the GROMOS96 constant pH simulations, whereas it is shifted by −0.2 pKa units in the OPLSA simulations. Overall, the force-field sensitivity seems to be small.
4.4. Imidazole
The titratable sites considered above in the dipeptide simulations interacted only via electrostatics. The chemical character of each site of the dipeptide (technically, its force-field parameters) was independent of the protonation state of the other sites, and the free energy of deprotonation of one site was affected only via Coulombic interactions with the other sites. Now, in contrast, we focus on two examples of “chemical coupling”, where two titratable sites interact also via chemical bonds. In this case, the chemical character, and, thus, the pKa value of a site, is affected by any change in the protonation state of the respective coupled site. As a first example, we consider the two chemically coupled titratable sites Nϵ and Nδ of imidazole (Figure 4). A second example, histidine, is discussed further below.
Constant pH simulations of imidazole were carried out for 22 pH values between pH 4 and pH 17. Each trajectory covered 20 ns, with 2 ns of equilibration and 18 ns of data collection. At pH values of 8–13, a barrier height of 0 kJ mol–1 was used, as discussed further below. Figure 9 shows the titration curve of imidazole, in which the cumulative deprotonation of both Nϵ and Nδ titratable sites is plotted as a function of pH. The first and second apparent pKa values of imidazole were estimated by a Henderson–Hasselbalch fit as described above, and are listed as Im(Nϵ + Nδ) in Table 4. The obtained apparent pKa values of 7.00 ± 0.12 and 14.78 ± 0.08 agree with the measured pKa values of 6.98 (from ref (62)) and 14.7 (from ref (1)). Note that the measured value for the imidazole second apparent pKa value, which was also used for the reference state, is replaced by the one of the chemically similar histidine, for which there are experimental data.(1)
Figure 9.
Titration curve of imidazole. The cumulative deprotonation (in equivalents, eq) of the two titratable sites (Nϵ and Nδ) is plotted as a function of pH. The dashed line is a fitted Henderson–Hasselbalch curve. The insets show the microscopic titration curves of sites Nϵ (black line) and Nδ (gray line) for the first (bottom graph) and second (top graph) deprotonation reaction of imidazole. Error bars were determined from the statistics of the observed transitions.
Table 4. Calculated and Measured pKa Values of Imidazole (Im) and Histidine (His).
| titratable site | calculated pKa | measured pKa |
|---|---|---|
| Imidazole | ||
| Im(Nϵ + Nδ) | 7.00 ± 0.12, 14.78 ± 0.08 | 6.98,(62) 14.7(1) |
| Im(Nϵ) | 7.29 ± 0.08, 14.51 ± 0.16 | 7.28,(62) 14.4(1) |
| Im(Nδ) | 7.28 ± 0.18, 14.46 ± 0.18 | 7.28,(62) 14.4(1) |
| Histidinea | ||
| His(Nϵ + Nδ) | 6.56 ± 0.21 | 6.42(62) |
| His(Nϵ) | 7.18 ± 0.23 | 6.92(62) |
| His(Nδ) | 6.70 ± 0.23 | 6.53(62) |
For histidine, only the first deprotonation reaction was investigated.
The microscopic pKa values of the Nϵ and Nδ sites (see Table 4) were estimated from the microscopic titration curves. These were obtained, similar to the C-terminus and Glu of the dipeptide, by plotting the fraction of deprotonated acid at one site, given that the other site was protonated (bottom inset in Figure 9; black for Nϵ, gray for Nδ), or deprotonated (top inset in Figure 9; black for Nϵ, gray for Nδ). The first and second microscopic pKa values were similar for Nϵ (7.29 ± 0.08 and 14.51 ± 0.16) and Nδ (7.28 ± 0.18 and 14.46 ± 0.18). This is expected, because the two titratable sites of imidazole are equivalent by symmetry. Consistently, the difference between the apparent and microscopic pKa values is approximately −(log10 2) and +(log10 2) for the first and second deprotonation reaction, respectively (see eqs 38 and 40, for the case where pKa,1 = pKa,2). This follows from the fact that the probability of deprotonating either two of the sites is twice the probability of deprotonating one of the sites.
Since the affinities of the Nϵ and Nδ titratable sites are identical, one expects to observe, at every pH value, similar corresponding average deprotonation levels, which provides an independent test of the statistical accuracy of the calculations. Accordingly, Figure 10 shows the average deprotonation ⟨λ⟩ (top left), and the number of transitions (bottom left) for Nϵ and Nδ, in black and gray, respectively, as a function of pH. Three ranges can be distinguished: (i) pH values close to 5 and 16, with similar ⟨λ⟩ of the two sites, and few transitions; (ii) pH values close to 7 and 14, with ⟨λ⟩ of Nϵ and Nδ also similar, but many transitions; and (iii) pH between 8 and 13, with marked differences for the average deprotonation between the two sites, and again few transitions. To enhance sampling in this last regime, and, thus, statistical accuracy, we lowered the barrier height of the biasing potential from 3 kJ mol–1 to 0 kJ mol–1, which is expected to increase the observed transitions, and repeated the calculations. As can be seen in the right side of Figure 10, the difference in average deprotonation is now significantly smaller, as, indeed, more transitions are observed. This example demonstrates how, by adjusting the barrier height, the transition frequency can be controlled and, thus, the accuracy can be enhanced.
Figure 10.
Average values (top) and number of transitions (bottom) of imidazole titration coordinates λNϵ (for site Nϵ, black) and λNδ (for site Nδ, gray). Constant pH simulations (of 20 ns) were carried out at each pH at barrier heights as indicated. Error bars denote estimates from the statistics of the observed transitions. Ranges (i), (ii), and (iii) are as referenced in the main text.
Note that, in range (i), close to pH 5 and 16, also few transitions occur, but the accuracy is much higher than for range (iii) at pH 8–13. This is due to the fact that, in range (iii), statistical fluctuations can favor one of the singly deprotonated forms over the other, whereas in range (i), only one form of imidazole is (mainly) sampled, fully protonated at pH close to 5, and fully deprotonated at pH close to 16. Therefore, insufficient sampling can result in a large inaccuracy in range (iii), as compared to the more straightforward case of range (i), where only one form is sampled.
Similar to range (iii), in range (ii), more than one form of imidazole is significantly sampled (fully protonated and neutral forms, and fully deprotonated and neutral forms, at pH close to 7 and 14, respectively). In this range, the inaccuracy is also larger than that observed in range (i). However, in contrast to range (iii), many more transitions are observed and, thus, sampling is enhanced. This is due to the fact that the free-energy difference between the protonated and deprotonated states of λ is small at pH values close to the pKa value, and the transition barrier is lower, implying more-frequent transitions.
4.4.1. Histidine
As a second example of chemical coupling, we considered histidine, which plays a crucial role in many biological processes, because its pKa value is close to the physiological pH. Accordingly, its protonation state changes with its local electrostatic environment. Here, we considered only biologically relevant pH values (pH <10), because no accurate force-field parameters for the negatively charged, fully deprotonated form of histidine at pH >10 are available.(47)
In the previous section, we have studied imidazole, which is the chemical moiety of the histidine side chain. The difference in the measured pKa values of histidine and imidazole is ∼0.5 pKa units,(62) with histidine having lower affinity for the proton (see Table 4). Moreover, in histidine, the affinities of the two sites are not identical, as in imidazole, but differ with respect to each other, also by ∼0.5 pKa units.(62) This situation enabled us to address the question of whether the constant pH simulation method is capable of quantitatively describing these differences (i.e., the effect of the presence of the backbone on the affinities for the proton of Nϵ and Nδ).
For this purpose, we parametrized the constant pH simulation, such that contributions to the proton affinities from the histidine backbone were not present in the reference state simulation, for which we used imidazole. Because of these contributions, the calculated pKa value is expected to be equal to the measured pKa value of histidine, and is expected to differ from the measured pKa value of the reference imidazole compound. Prior to starting the constant pH simulations, however, the contribution to the affinities from the different force-field parameters of imidazole and histidine were calculated. The thermodynamic cycle in Figure 3 served this purpose (i.e., to compute the free energies of transferring imidazole parameters to histidine parameters for each of the protonation states). Table 5 shows the free energies that have been obtained. As can be seen, these are similar to each other (between −12.59 kJ mol–1 and −14.36 kJ mol–1), except for the neutral form (01). In this form, Nϵ is protonated, whereas Nδ, which is two bonds away from the backbone Cβ, is deprotonated. The free energies in Table 5 were then used to redefine the reference state (see eq 33) prior to starting the simulations.
Table 5. Free Energies of Transfer (ΔGtransf) of Each Imidazole Protonation State (see Figure 4) to the Corresponding Histidine State.
| protonation state | ΔGtransf (kJ mol –1) |
|---|---|
| 00 (+) | –12.59 ± 0.54 |
| 10 (Nδ+) | –0.04 ± 0.61 |
| 01 (Nϵ+) | –13.68 ± 0.55 |
| 11 (−) | –14.36 ± 0.59 |
Constant pH simulations of histidine were carried out for 15 pH values between pH 4 and pH 10. Each trajectory covered 20 ns of simulation time with 2 ns of equilibration time and 18 ns of data collection time. Similar to imidazole, for pH values between 8 and 10, a barrier height of 0 kJ mol–1 was used. Figure 11 shows the obtained titration curve. The calculated pKa value of 6.56 ± 0.21, estimated via a Henderson–Hasselbalch fit (dashed line), agrees with the measured pKa value of 6.42 (see Table 4). Thus, the ∼0.5 pKa units downward shift in the pKa value of histidine, with respect to the reference compound (imidazole), was calculated within the statistical error (see Table 4).
Figure 11.
Titration curve of histidine. The cumulative deprotonation (in equivalents, eq) of the two titratable sites (Nϵ and Nδ) is plotted as a function of pH. The dashed line is the fitted Henderson–Hasselbalch curve. The inset shows the microscopic titration curves of the Nϵ and Nδ (in black and gray, respectively). Error bars were determined from the statistics of the observed transitions.
The inset of Figure 11 shows the microscopic titration curves, which were obtained as described above for imidazole and Glu-Ala. Henderson–Hasselbalch fits to these curves yielded microscopic pKa curves of 7.18 ± 0.23 for Nϵ and 6.70 ± 0.23 for Nδ, which is consistent with a macroscopic pKa value of 6.56 (see eq 38). The difference of 0.48 pKa units between the two microscopic pKa values agrees with the measured value of 0.39 pKa units (see Table 4). Thus, in addition to decreasing the affinity of the two sites, the effect of the histidine backbone manifests itself with a shift in the pKa of the two titratable sites with respect to each other, with Nϵ having a higher affinity than Nδ.
5. Discussion and Conclusions
We have developed a framework to describe changes in protonation states at constant pH, where the requirements of (i) sampling of the relevant λ configurational space, with conformations being the protonated (λ = 0) and deprotonated (λ = 1) states, (ii) control of the rate of transition between the two states, and (iii) fully atomistic description of the system are fulfilled. The method, which was implemented within the molecular dynamics (MD) package GROMACS,37−39 is based on the λ-dynamics approach of Kong and Brooks,(32) and it follows, in the main lines, the constant pH simulation method by Brooks and co-workers.32,34,35 A new general approach was developed to treat chemically coupled sites, and it was applied to describe the proton tautomerism of imidazole and histidine. In proteins, other examples of chemical coupling are coordinating residues around metal ions, such as that observed in copper binding sites(65) or zinc binding sites.(66)
In order to test whether, and under which conditions ,the above-mentioned requirements are actually fulfilled by our method, constant pH simulations of four systems, glutamic acid, Glu-Ala dipeptide, imidazole, and histidine, were carried out. In the following, we will briefly discuss these results in light of the aforementioned requirements, and then we will address the questions of how accurately the calculated average protonation agreed with the measured pKa values, and whether the method is capable of describing interacting titratable sites. In particular, two types of interactions were considered: those between chemically uncoupled sites, which interact only via electrostatics, and those between chemically coupled sites, for which a new coupling scheme was developed.
During the constant pH simulations, the average λ in the protonated and deprotonated states was found to be very close to values of 0 or 1, respectively, as required to describe the system in a physically realistic way. This was achieved by appropriately increasing the radius that defines the circular degree of freedom that is used. Similarly, sampling of the intermediate unphysical states was minimized by introducing suitable biasing potentials, in addition to the entropic barrier (of a few kJ mol–1) implied by the angular degree of freedom. It was shown that, for a 3 kJ mol–1 biasing potential barrier height, more than 70% of the simulation time was spent close to physical states (λ < 0.1 and λ > 0.9).
Adjusting the barrier of the biasing potential also allowed us to control the transition rate, as demonstrated for glutamic acid and imidazole. In particular, for imidazole, it was shown how the accuracy of the calculations at pH values between 8 and 13 was significantly enhanced by increasing the transition rate, thus achieving fast sampling of different protonation states.
In all systems investigated, a fully atomistic description was used, including an explicit solvent. Interestingly, we found that the average residence time at the protonated and deprotonated states is more than 2 orders of magnitude larger than that for comparable systems simulated with the λ-dynamics constant pH approach developed by Brooks and co-workers34,35 with an implicit solvent. The choice of the thermostat is critical, as shown in Figure 6, where the average residence time is three times larger for the Andersen thermostat, compared to the Berendsen thermostat. Note that the transitions observed in the simulations with the Berendsen thermostat were partially correlated, which reduced the statistical accuracy. However, the thermostat alone does not seem to explain the differences between simulations in implicit and explicit solvents. Thus, the explicit description of water is likely to be crucial as well. We note that the fluctuations in the effective barrier for a transition are quite large due to the water dipoles. These effects, which are important for the kinetics of proton transfer, are not described in implicit water. It would certainly be interesting to study these in more detail.
For the first test system (glutamic acid), the calculated titration curve agreed very well with the measured one. Although this result may seem trivial, as the constant pH simulation was parametrized via the measured pKa value of glutamic acid (the reference state), it nevertheless shows that the effect of pH is taken into account correctly. As expected, an increase of the total simulation time from 4.5 ns to 18 ns significantly improved accuracy. By increasing the length of the simulation, on one hand, the number of transitions increases, and, on the other hand, a more extensive sampling of the configurational space of the side chain at a certain protonation state is achieved. Both factors enhanced the accuracy of the simulation. Note that adjusting the barrier height of the biasing potential allows one to study the relaxation effects that are due to the change in protonation state.
To study the interaction between titratable sites, we further considered the dipeptide Glu-Ala as a test case. Here, we expected the interactions in the dipeptide to shift the calculated pKa values, with respect to the values of the individual titratable sites (the reference states). Indeed, the calculated pKa values were all shifted to favor the charge states of the titratable sites. This was more evident for Glu and N-terminus, which moved closer to each other in the pH range at which they were mainly in their charged states. The C-terminus and Glu had rather similar pKa values (∼3), and the individual contributions of these two groups to the deprotonation of the dipeptide were distinguishable only in the site-specific titration curves. By analyzing the microscopic pKa values, the interaction between these two titratable sites was estimated as ∼1 kJ mol–1. The Hill coefficient of 0.82 for the titration curve of the C-terminus indicated anticooperativity in the system, in agreement with the microscopic pKa values. We note that, by calculating the microscopic pKa values, this anticooperativity was quantified here, in terms of free energy.
For Glu-Ala, the titratable sites interacted only via electrostatics. In contrast, in imidazole, which was the third system considered, the titratable sites Nϵ and Nδ interacted chemically, because the affinity for the proton of one site is a function of the protonation state of the respective other site. To describe this type of interaction, a general approach was developed, in which each site is described by a titration coordinate λ, and coupling between the sites is explicitly taken into account. Note that this approach was applied here to describe the tautomerism of imidazole and histidine, but it can be used to describe chemical coupling between any two or more sites. Moreover, we showed that our general approach simplifies to the case of chemically uncoupled sites when interactions occur only via electrostatics. The approach of describing each site of a tautomer as a separate titratable site (or pseudo-site) is not new.(67) However, to avoid the occurrence of the double deprotonated state at pH 7, we do not introduce an arbitrary energy penalty.(67) Instead, the reference states of the pseudo-sites are coupled, such that they are a function of the protonation state of the titratable site. For example, in histidine, the reference pKa value of one of the sites on the side chain increases from ∼6 to ∼14 as the respective other site deprotonates. Therefore, at pH 7, a second deprotonation is highly improbable. Alternatively, in the constant pH approach of Khandogin and Brooks,(35) tautomerism of titratable amino acids is described by considering three states only. In practice, only one titration coordinate is used, whereas an additional continuous coordinate controls the interconversion between the two tautomeric forms.(35) We note that, by appropriately choosing the protonation states, a three-state description also is obtained within our approach.
We did not use a tautomeric model for Glu in this work. However, it is straightforward to apply such a model to Glu as well, to allow for deprotonation/protonation of both oxygens on the carboxylic group. In particular, such a description is required in protein simulations, in which specific intramolecular interactions can significantly increase the barrier for rotation of the carboxylic group.
The obtained titration curve of imidazole agreed well with the measured one. To test the model, we simulated over a large pH range, to also observe the doubly deprotonated state. Although, at physiological pH, this form is quite unlikely to occur, it cannot be excluded that, in the presence of particular interactions, it plays a role as well.
Histidine was considered as a second example of chemically interacting sites. Here, we investigated the shift of the calculated proton affinity, with respect to the reference one, because of the presence of the backbone. For these simulations, the reference state was transformed to a similar one by means of the thermodynamic cycle shown in Figure 3. In general, the reference state is chosen such that the chemical character of the titratable site is similar in the reference and simulated states(28) (i.e., that all differences are described via electrostatics). This implies that one is restricted to those states for which experimental data are available. Now we have proposed an approach that allows one to use a less similar state, therefore, broadening the range of accessible systems.
Finally, we would like to note that our constant pH approach will also be useful for determining protonation states from X-ray structures. A constant pH MD simulation is performed before the production run is started. During this equilibration phase, position restraints can be applied to the protein backbone, or heavy atoms, to keep the atomic coordinates close to the X-ray data. This procedure might be particularly useful for proteins, in which internal water molecules play a role in stabilizing protonation states.(68)
Acknowledgments
The authors thank Berk Hess from the University of Stockholm, Sweden, for helpful discussions and Ulrike Gerischer for proofreading the manuscript.
Supporting Information Available
In the Supporting Information, Tables s1, s2, and s3 list the side-chain atomic charges of histidine and imidazole, the contribution of bonded terms to the deprotonation free energy of glutamic acid, and the coefficients of polynomial fits for the reference states, respectively. Figures s1 and s2 show the titration curves calculated with GROMOS96(50) and OPLSA(51) force fields, of Glu with neutral termini, and of the tripeptide Ala-Glu-Ala, respectively. The error estimate for the average protonation state via bayesian approach is also presented. This information is available free of charge via the Internet at http://pubs.acs.org/.
Author Present Address
† Institute of Computer Science, Georg August University, Göttingen, Germany.
Supplementary Material
References
- Creighton T. E.Proteins: Structures and Molecular Properties; W. H. Freeman and Company: New York, 1993. [Google Scholar]
- Dobson C. M. Nature 2003, 426, 884–890. [DOI] [PubMed] [Google Scholar]
- Haas J.; Vöhringer-Martinez E.; Bögehold A.; Matthes D.; Hensen U.; Pelah A.; Abel B.; Grubmüller H. Chem. Biol. Chem. 2009, 10, 1816–1822. [DOI] [PubMed] [Google Scholar]
- Stouffer A. L.; Acharya R.; Salom D.; Levine A. S.; Costanzo L. D.; Soto C. S.; Tereshko V.; Nanda V.; Stayrook S.; DeGrado W. F. Nature 2008, 451, 596–599. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schnell J. R.; Chou J. J. Nature 2008, 451, 591–595. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tournaire-Roux C.; Sutka M.; Javot H.; Gout E.; Gerbeau P.; Luu D.-T.; Bligny R.; Maure C. Nature 2003, 425, 393–397. [DOI] [PubMed] [Google Scholar]
- Wiley D. C.; Skehel J. J. Annu. Rev. Biochem. 1987, 56, 365–394. [DOI] [PubMed] [Google Scholar]
- Popov K.; Ronkkomaki H.; Lajunen L. H. J. Pure Appl. Chem. 2006, 78, 663–675. [Google Scholar]
- Allen R. I.; Box K. J.; Comer J. E. A.; Peake C.; Tam K. Y. J. Pharm. Biomed. Anal. 1998, 17, 669–741. [DOI] [PubMed] [Google Scholar]
- Bashford D.; Karplus M. Biochemistry 1990, 29, 10219–10225. [DOI] [PubMed] [Google Scholar]
- Ullmann G. M.; Knapp E.-W. Eur. Biophys. J. 1999, 28, 533–551. [DOI] [PubMed] [Google Scholar]
- Mongan J.; Case D. A.; McCammon J. A. J. Comput. Chem. 2004, 25, 2038–2048. [DOI] [PubMed] [Google Scholar]
- Lolis E.; Petsko G. A. Biochemistry 1990, 29, 6619–6625. [DOI] [PubMed] [Google Scholar]
- Kozlov A. G.; Lohman T. M. Proteins: Struct. Funct. Bioinf. 2000, 41, 8–22. [Google Scholar]
- Tamm L. K.; Han X. Biosci. Rep. 2000, 20, 501–518. [DOI] [PubMed] [Google Scholar]
- Cohen F. S.; Melikyan G. B. Nat. Struct. Biol. 2001, 8, 653–655. [DOI] [PubMed] [Google Scholar]
- Warshel A.; Levitt M. J. Mol. Biol. 1976, 103, 227–249. [DOI] [PubMed] [Google Scholar]
- Warshel A.; Weiss R. M. J. Am. Chem. Soc. 1980, 102, 6218–6226. [Google Scholar]
- Day T. J. F.; Soudackov A. V.; Čuma M.; Schmitt U. W.; Voth G. A. J. Chem. Phys. 2002, 117, 5839–5849. [Google Scholar]
- Brancato G.; Tuckerman M. E. J. Chem. Phys. 2005, 122, 224507. [DOI] [PubMed] [Google Scholar]
- Maupin C. M.; Wong K. F.; Soudackov A. V.; Kim S.; Voth G. A. J. Phys. Chem. A 2006, 110, 631–639. [DOI] [PubMed] [Google Scholar]
- Lill M. A.; Helms V. J. Chem. Phys. 2001, 114, 1125–1132. [Google Scholar]
- Cymes G. D.; Ni Y.; Grosman C. Nature 2005, 438, 975–980. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mongan J.; Case D. A. Curr. Opin. Struct. Biol. 2005, 15, 1–7. [DOI] [PubMed] [Google Scholar]
- Baptista A. M.; Teixeira V. H.; Soares C. M. J. Chem. Phys. 2002, 117, 4184–4200. [Google Scholar]
- Dlugosz M.; Antosiewicz M. Chem. Phys. 2004, 302, 161–170. [Google Scholar]
- Bürgi R.; Kollman P. A.; van Gunsteren W. F. Proteins: Struct. Funct. Bioinf. 2002, 47, 469–480. [DOI] [PubMed] [Google Scholar]
- Börjesson U.; Hünenberger P. H. J. Chem. Phys. 2001, 114, 9706–9719. [Google Scholar]
- Baptista A. M. J. Chem. Phys. 2002, 116, 7766–7768. [Google Scholar]
- Berendsen H. J. C.; Postma J. P. M.; van Gunsteren W. F.; Nola A. D. J. Chem. Phys. 1984, 81, 3684–3690. [Google Scholar]
- Mertz J. E.; Pettitt B. M. Int. J. Supercomput. Appl. High Perform. Eng. 1994, 8, 47–53. [Google Scholar]
- Kong X.; Brooks III C. L. J. Chem. Phys. 1996, 105, 2414–2423. [Google Scholar]
- Abrams J. B.; Rosso L.; Tuckerman M. E. J. Chem. Phys. 2006, 125. [DOI] [PubMed] [Google Scholar]
- Lee M. S.; Salsbury J. F. R.; Brooks III C. L. Proteins: Struct. Funct. Bioinf. 2004, 56, 738–752. [DOI] [PubMed] [Google Scholar]
- Khandogin J.; Brooks III C. L. Biophys. J. 2005, 89, 141–157. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wallace J. A.; Shen J. K. Methods Enzymol. 2009, 466, 455–475. [DOI] [PubMed] [Google Scholar]
- Berendsen H. J. C.; van der Spoel D.; van Drunen R. Comput. Phys. Commun. 1995, 91, 43–56. [Google Scholar]
- Lindahl E.; Hess B.; van der Spoel D. J. Mol. Model. 2001, 7, 306–317. [Google Scholar]
- van der Spoel D.; Lindahl E.; Hess B.; Groenhof G.; Mark A.; Berendsen H. J. Comput. Chem. 2005, 26, 1701–1718. [DOI] [PubMed] [Google Scholar]
- Kirkwood J. G. J. Chem. Phys. 1935, 3, 300–313. [Google Scholar]
- van der Vegt N. F. A.; Briels W. J. J. Chem. Phys. 1998, 109, 7578–7582. [Google Scholar]
- Andersen H. C. J. Chem. Phys. 1980, 72, 2384–2393. [Google Scholar]
- Warshel A.; Sussman F.; King G. Biophysics 1985, 25, 8368–8372. [DOI] [PubMed] [Google Scholar]
- Kollman P. A. Chem. Rev. 1993, 93, 2395–2417. [Google Scholar]
- Hwang J.-K.; Warshel A. J. Am. Chem. Soc. 1987, 109, 715–720. [Google Scholar]
- Simonson T.; Archontis G.; Karplus M. Acc. Chem. Res. 2002, 35, 430–437. [DOI] [PubMed] [Google Scholar]
- van Gunsteren W. F.; Billeter S. R.; Eising A. A.; Hünenberger P. H.; Krüger P.; Mark A. E.; Scott W. R. P.; Tironi I. G.. Biomolecular Simulation: GROMOS96 Manual and User Guide; BIOMOS b.v.: Zürich, Switzerland, and Groningen, The Netherlands, 1996. [Google Scholar]
- Onufriev A.; Case D. A.; Ullmann G. M. Biochemistry 2001, 40, 3413–3419. [DOI] [PubMed] [Google Scholar]
- Klingen A. R.; Bombarda E.; Ullmann G. M. Photochem. Photobiol. Sci. 2006, 5, 588–596. [DOI] [PubMed] [Google Scholar]
- Oostenbrink C.; Villa A.; Mark A. E.; van Gunsteren W. F. J. Comput. Chem. 2004, 25, 1656–1676. [DOI] [PubMed] [Google Scholar]
- Berendsen H. J. C.; Postma J. P. M.; van Gunsteren W. F.; Hermans J.. Interaction models for water in relation to protein hydratation. In Intermolecular Forces; Pullman B., Ed.; D. Reidel: Dordrecht, The Netherlands, 1981; pp 331–342. [Google Scholar]
- Darden T.; York D.; Pedersen L. J. Chem. Phys. 1993, 98, 10089–10092. [Google Scholar]
- Essmann U.; Perera L.; Berkowitz M. L.; Darden T.; Lee H.; Pedersen L. G. J. Chem. Phys. 1995, 103, 8577–8592. [Google Scholar]
- Miyamoto S.; Kollman P. A. J. Comput. Chem. 1992, 13, 952–962. [Google Scholar]
- Hess B.; Bekker H.; Berendsen H. J. C.; Fraaije J. G. E. M. J. Comput. Chem. 1997, 18, 1463–1472. [Google Scholar]
- Jorgensen W. L.; Maxwell S.; Tirado-Rives J. J. Am. Chem. Soc. 1996, 118, 11225–11236. [Google Scholar]
- Jorgensen W. L.; Chandrasekhar J.; Madura J. D.; Impey R. W.; Klein M. L. J. Chem. Phys. 1983, 79, 926–935. [Google Scholar]
- Hünenberger P. H.; McCammon J. A. J. Chem. Phys. 1999, 110, 1856–1872. [Google Scholar]
- Hummer G.; Pratt L. R.; Garcia A. E. J. Phys. Chem. 1996, 100, 1206–1215. [Google Scholar]
- Bundi A.; Wüthrich K. Biopolymers 1979, 18, 285–297. [Google Scholar]
- Thurlkill R. L.; Grimsley G. R.; Scholtz J. M.; Pace C. M. Protein Sci. 2006, 15, 1214–1218. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tanokura M. Biochim. Biophys. Acta 1983, 742, 576–585. [DOI] [PubMed] [Google Scholar]
- Flyvbjerg H.; Petersen H. G. J. Chem. Phys. 1989, 91, 461–466. [Google Scholar]
- Hess B. J. Chem. Phys. 2002, 116, 209–217. [Google Scholar]
- Xie Y.; Inoue T.; Miyamoto Y.; Matsumura H.; Kataoka K.; Yamaguchi K.; Nojini M.; Suzuki S.; Kai Y. J. Biochem. 2005, 137, 455–461. [DOI] [PubMed] [Google Scholar]
- Mehle A.; Thomas E. R.; Rajendran K. S.; Gabuzda D. J. Biol. Chem. 2006, 281, 17259–17265. [DOI] [PubMed] [Google Scholar]
- Baptista A. M.; Soares C. M. J. Phys. Chem. B 2001, 105, 293–309. [Google Scholar]
- Damjanovic A.; Brooks B. R.; Garcia-Moreno B.. J. Phys. Chem. A 2011, 115, 4042–4053. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.