Abstract
The purpose of this work was to design and implement constant adiabadicity gradient modulated pulses that have improved slice profiles and reduced artifacts for spectroscopic imaging on 3T clinical scanners equipped with standard hardware. The newly proposed pulses were designed using the gradient offset independent adiabaticity (GOIA, Tannus and Garwood, 1997) method using WURST modulation for RF and gradient waveforms. The GOIA-WURST pulses were compared with GOIA-HSn (GOIA based on nth-order hyperbolic secant) and FOCI (Frequency Offset Corrected Inversion) pulses of the same bandwidth and duration. Numerical simulations and experimental measurements in phantoms and healthy volunteers are presented. GOIA-WURST pulses provide improved slice profile that have less slice smearing for off-resonance frequencies compared to GOIA-HSn pulses. The peak RF amplitude of GOIA-WURST is much lower (40% less) than FOCI but slightly higher (14.9% more) to GOIA-HSn. The quality of spectra as shown by the analysis of line-shapes, eddy currents artifacts, subcutaneous lipid contamination and SNR is improved for GOIA-WURST. GOIA-WURST pulse tested in this work shows that reliable spectroscopic imaging could be obtained in routine clinical setup and might facilitate the use of clinical spectroscopy.
Keywords: Magnetic Resonance Spectroscopic Imaging (MRSI), Chemical Shift Displacement Error (CSDE), Specific Absorption Rate (SAR), Gradient Offset Independent Adiabatic (GOIA), LASER (Localized Adiabatic Selective Refocusing)
1. INTRODUCTION
Metabolite levels measured by MR spectroscopy are highly correlated with healthy or pathological status of a tissue. Mapping spatial distribution of metabolites with MR spectroscopic imaging (MRSI, also known as chemical shift imaging or CSI) [1,2] can increase specificity of MRI, especially in clinical conditions (i.e. brain tumors [3], stroke [4], psychiatric disorders [5]) where access for invasive (biopsies) or serial investigations is difficult.
MRSI performed at high field benefits from increased spectral resolution which allows better separation and identification of metabolites. However, obtaining reliable MRSI information at high field is limited by a number of challenges such as: i) chemical shift displacement error (CSDE), ii) spatial non-uniformity of RF excitation and iii) contamination with large lipid signal from tissues outside the region of interest (ie. subcutaneous fat). Signal localization using slice selective pulses and gradients in spectroscopy can not distinguish between a change in frequency due to chemical shift or due to gradients, resulting in a spatial shift (CSDE) of the excited slice for each metabolite. RF inhomogeneity becomes more problematic at high fields as RF wavelength becomes comparable with object dimensions. Contamination (“voxel bleeding”) with lipid signal in MRSI can create large artifacts when CSDE and imperfect slice profiles combine unfavorably with poor point spread function (PSF) due to limited phase encoding. Improvement of CSDE and slice profiles can reduce greatly the source of lipid “voxel bleeding”.
Adiabatic pulses are known for a long time in NMR spectroscopy [6,7] as a method to compensate for RF inhomogeneity and achieve wide inversion bandwidths (BW) with limited RF field amplitude. Hence they are natural candidates for MRSI, where a large BW is necessary to reduce CSDE. However, their direct use in MRSI is complicated by long pulse durations when wide BW are sought and the fact that a pair of two adiabatic pulses is necessary to produce a refocusing echo [8], resulting in long echo times and increased specific absorption rate (SAR). In many instances of in-vivo applications [9] conventional adiabatic pulses need 5 ms to achieve 5 kHz bandwidth due to RF power limitations. An effective method to reduce RF amplitude is to apply VERSE (Variable Rate Selective Excitation) method [10,11]. VERSE uses gradient modulation to decrease peak RF amplitude, and adiabatic pulses with very large BW (20 kHz) and short duration (3.5 ms) have been designed [12,13] for localized MRS. FOCI (Frequency Offset Corrected Inversion) pulse appears to have been used more in human studies [12,14,15] compared to GOIA (Gradient Offset Independent Adiabaticity) pulses [13,16]. However these demonstrations have been performed mainly on research scanners and despite their benefits, these pulses are not widespread for MRSI on clinical systems.
A remarkable property of GOIA pulses is the constant adiabatic factor over the entire spectral BW, while for FOCI and conventional adiabatic pulses the adiabatic factor degrades away from the central frequency. Another important advantage is that GOIA pulses require less RF power than FOCI pulse for the same BW and pulse duration. In contrast to previous investigators [13] who designed GOIA based on nth-order hyperbolic secant (HSn) functions, we propose [17] new type of GOIA pulses starting from WURST [18] modulation for both RF field and gradient. As shown later, more favorable slew rates can be found for WURST gradient waveforms. A specific aim was to find robust pulses that need less than 1 kHz (23.4 µT) peak RF amplitude for a BW of 20 kHz and duration of 3.5 ms. For example the FOCI pulse with the same specifications would need 1.46 kHz for optimal operation. This is important especially on clinical 3T scanners where pulses delivered by the transmit body coil are generally limited to 1 kHz peak amplitude in-vivo. Additionally, decreasing the RF power enables shorter repetition times (TR = 1.5 s or shorter) to be used with adiabatic pulses MRSI in clinical conditions where acquisition time is limited (sequences with conventional adiabatic pulses might require TR of 3s or longer to compensate for specific absorption rate (SAR)). Although improved RF homogeneity with reduced RF power deposition at high field can be achieved using parallel transmit arrays [19,20], this is still an area of active research and parallel transmit systems are not yet largely available and affordable.
In particular, we find that the GOIA pulse combination of WURST-16 for RF field and WURST-4 for the gradient modulations, which we name GOIA-W(16,4), provides improved spectra quality with regard to SNR, coupled spins spectra, eddy current artifacts and lipid contamination compared to results obtained with GOIA based on HSn and FOCI pulses. Performance of all the pulses is tested extensively in numerical simulations and experiments on phantoms and volunteers. Results are also compared to the more widely used PRESS [22] localization employing Mao [23] refocusing pulses. Further tests and results obtained on clinical patients with brain tumors or stroke will be communicated separately.
2. THEORY
Chemical shift displacement error of a particular metabolite increases linearly with the size of the main magnetic field and is inversely proportional with the bandwidth of the slice selective pulse:
| [1] |
where Δδ is the difference (in ppm) between the chemical shift (δ) of the metabolite and the carrier frequency of the RF field, B0 the main magnetic field (in frequency units) and BW is the bandwidth of RF pulse. Hence, increasing pulse BW is highly desirable to reduce CSDE.
It can be noticed that the same linear dependency that improves spectral resolution by increasing the B0 field also worsens the CSDE in Eq. [1]. Considering a minimum of 3.5 ppm for the spectral range (4.3 - 0.8 ppm) of 1H MRSI, the frequency difference over the entire spectrum at 3T is approximately 450 Hz (1.05 kHz at 7T). Under these conditions, GOIA or FOCI pulses (BW = 20 kHz) will have a minimal ~2% displacement, while conventional adiabatic pulses (BW = 5 kHz) will give ~10% CSDE. By comparison, Mao pulses with BW of 1.2 kHz used in PRESS have a large CSDE of 38%. This can be especially detrimental for coupled spins like lactate with large chemical shift difference (4.09 and 1.31 ppm) where signal loss results due to combination of flip angles distribution (leading to polarization transfer and multiple quantum coherences) and CSDE [24].
Most generally, the adiabatic condition in the case of a gradient modulated adiabatic pulse is given by [13]:
| [2] |
where B1(t) is the modulation of the RF amplitude, ω(t) is the modulation of the carrier frequency, Ω is the chemical shift offset, G(t) is the modulation of the gradient, z is the position and γ is the giromagnetic ratio (B1(t), ω(t) and Ω are specified in frequency units).
GOIA can be defined [13] by imposing that the adiabatic factor Q(Ω,t) is constant for all chemical shifts (Ω), obtaining:
| [3] |
Due to hardware requirements that need well behaved RF and gradient waveforms, Eq. [3] is used to find the frequency modulation ω(t) after choosing B1(t) and G(t) functions:
| [4] |
where ωc is the center frequency specified by the condition ω(Tp/2) = 0. In practice, the phase modulation is used to sweep the frequency:
| [5] |
Eqs. [4] and [5] can be numerically integrated for the most general B1(t) and G(t) functions. In order to excite a slice at an arbitrary position (off-isocenter) the RF carrier frequency has to follow the gradient modulation. This can be achieved by calculating an additional phase modulation
| [6] |
which is superimposed on the phase obtained from Eq. [5] leading to the final phase modulation
| [7] |
Using Eq [5], we constructed two types of GOIA pulses [17] starting from the n-order hyperbolic secant (HSn) [25] functions:
| [8] |
and WURST (Wn) [18] functions:
| [9] |
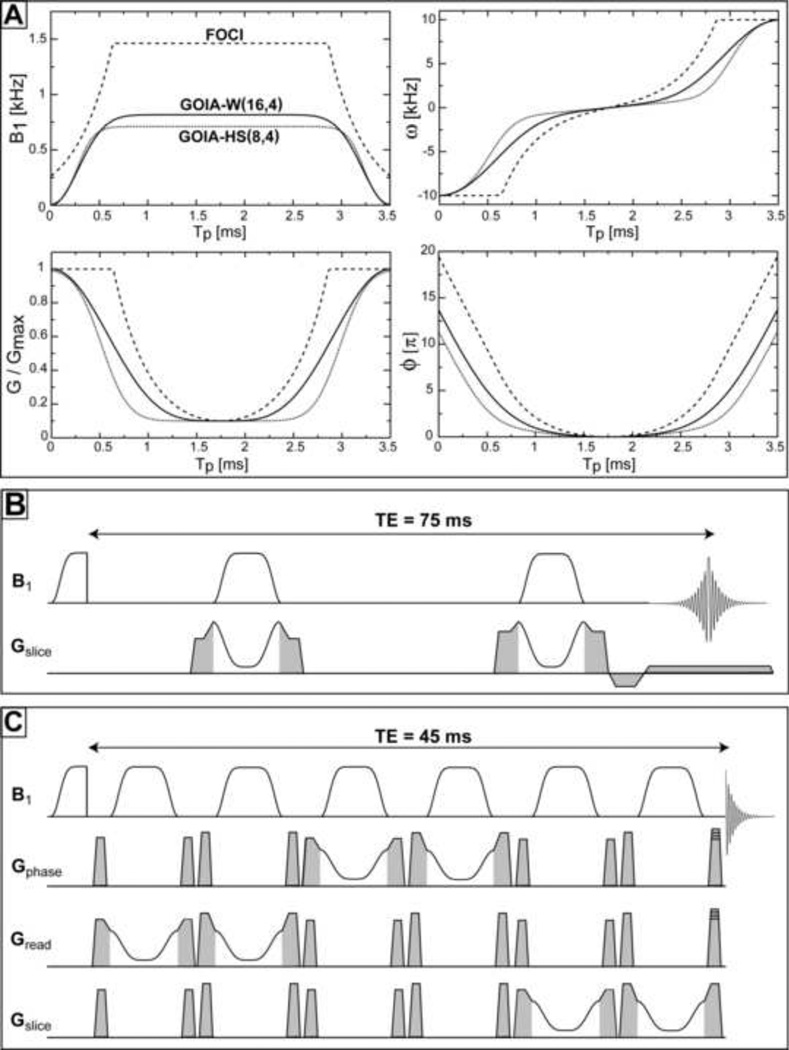
where Tp is the pulse duration (0 ≤ t ≤ Tp), B1,max the maximum RF amplitude (β = 5.33 defines the cut-off value for HS pulse), Gmax the maximum gradient and f ∈ [0,1] is the gradient modulation factor. The larger the f factor the more gradient drops in the middle of the pulse and less B1,max is required. A value of f = 0.9 is typically chosen (gradient in the middle of the pulse is 10% from the maximum value) and we have used it for both GOIA and FOCI pulses. Generally, the n and m orders for B1 and G modulations are chosen to be different (m < n) and we adopt the following naming convention: GOIA-X(n,m) with X specifying the base modulation function (HS or W), n the order of B1 modulation, and m the order of gradient modulation (the shapes of GOIA-W(16,4) and GOIA-HS(8,4) can be seen in Fig. 1A).
Figure 1.
Adiabatic pulses: A) Modulations of RF amplitude (B1(t)), gradient (G(t)), carrier frequency (ω (t)) and phase (ϕ(t)) for GOIA-W(16,4) (solid line), GOIA-HS(8,4) (dotted line) and FOCI (dashed line). RF amplitude and slew rate requirements are maximum in the case of FOCI pulse; B) Pulse sequence to measure slice profiles with double adiabatic passage spin echo, spoiler, prephase and readout gradients are shown in grey; C) LASER sequence with GOIA pulses for localized spectroscopy, spoiler gradients are shown in grey, phase encoding gradients are superimposed on the last spoiler for MRSI applications.
The design of GOIA pulses can be improved by predicting their slice profiles and spectra. Slice profiles and spectra of isolated spins can be readily obtained through classical Bloch equations, however to compute spectra of coupled spins the full quantum mechanics formalism [26] is needed. Considering a J-coupled spin system, their Hamiltonian in the rotating frame is given by:
| [10] |
where Ωp and Jpq are the chemical shift offset and the scalar coupling, respectively (in frequency units), Îα,p (α = x,y,z) and Îp denote the spins operators, and B1(t), G(t) and ϕ(t) are defined as above. Only the most mobile metabolites are considered, neglecting the anisotropic interactions such as chemical shielding anisotropy and dipolar couplings.
The spin evolution under the time dependent Hamiltonian of Eq. [10] is given by the solution of Liouville-von-Neumann equation of motion (neglecting relaxation):
| [11] |
that can be calculated through the means of Average Hamiltonian Theory (AHT) in the case of a periodic perturbation or using Floquet Theory for a more general case [27]. An analytical solution for Eq. [11] including the numerically calculated phase modulation of Eq. [5] would provide little insight. Instead we use numerical simulations, detailed in the next section, to visualize the performance of GOIA pulses under various conditions.
3. METHODS
3.1 Numerical simulations
Quantum mechanical simulations were performed in GAMMA [28] to predict slice profiles and spectra of coupled spins with GOIA or FOCI pulses of 3.5 ms duration and 20 kHz bandwidth. Slice profiles are calculated considering a double refocusing spin echo [8] obtained with a pair of adiabatic pulses. Simulations of localized spectra are done for a symmetric LASER sequence [21] and using published metabolite chemical shifts and scalar couplings [29]. The adiabatic pulses and the pulse sequences for slice profile and LASER spectroscopic measurements are shown in Fig. 1.
In all simulations spin evolution was calculated using a piece-wise constant Hamiltonian. A minimum time step of 20 µs was found to be sufficient in simulations that produce the same results for shorter time steps. GOIA and FOCI pulses were defined with the same number of support points (175 points for 3.5 ms) which were identical in simulations and experiments. The minimum number of samples necessary to accurately reproduce the waveform is 70, given by the time-bandwidth (R factor, [13]) product (Nyquist condition). The phase modulation was calculated by trapeze numerical integration according to Eq. [5] but using B1(t) and G(t) functions with finer resolution (for each integration step one point was obtained by summing 10 underlying points). To select off-isocenter slices the final phase modulation is obtained by the phase combination from Eq. [7].
For slice profiles simulations, a one-dimensional object of length L was divided into a large number N of infinitesimal sections. The offset (γzG) induced by the gradient was considered to be constant across an infinitesimal section and the spin evolution was calculated independently for each section. To obtain the slice profile, the magnetization for each group of 20 adjacent sections was summed (20 was found to be a good compromise between the minimum number of directions for the phase cancellation of transverse magnetization in sections outside the slice and the spatial resolution required to define the slice profile). For spectra simulations the FID of each section was calculated and a combined FID was obtained by averaging across all sections before FFT.
Symmetry in the pulse shapes and periodicity in the spin evolution under double spin echo for slice profile or six spin echo (LASER) for spectra were exploited to speed-up calculations. The same echo times (TE) used to simulate slice profiles or spectra were employed in experiments.
3.2 Experiments
All the measurements were done on 3T Magnetom Tim Trio systems (Siemens, Erlangen). The RF body coil was used for transmit and the 12-channel head matrix or the 32-channel head phased array were used for receive. The maximum amplitude of B1 field delivered by the transmit body coil is limited to 1 kHz (23.4 µT) for in-vivo applications. The whole-body gradient system (TQ-engine) specifications include a maximum nominal amplitude of 26 mT/m and a maximum slew rate of 170 mT/(m*ms).
Pulse and gradient modulations where implemented in the IDEA environment (VB15A) using arbitrary classes and calculated inside the sequence preparation block. The gradient hardware needs a raster time of 10 µs which is faster than the RF raster time of 20 µs. To match the time steps an initial gradient shape is calculated with 175 points (20 µs raster) which is expanded to 350 points in the final shape by duplicating each point with itself. For selecting off-isocenter slices the shift in carrier frequency was implemented by calculating the corresponding phase modulation (Eq. [6]) which was added to the phase modulation of Eq. [5]. The same approach was used in numerical simulations.
Slice profiles were obtained using the spin echo from a pair of adiabatic pulses according to Fig. 1B. Gradient spoilers are 8 mT/m and 1.9 ms (700 µs ramp-up/down times) around first pulse, and 10 mT/m and the same duration around the second pulse. The slice profile was read with a small gradient (2 mT/m) applied along the slice selection direction which was preceded by the corresponding pre-phasing gradient (2 ms total duration). A spectral window of 40 kHz and 1k points were used for acquisition. A minimum echo time of 75 ms was used and a repetition time of 1.5 s.
Spectra were obtained with the symmetric LASER sequence of Fig. 1C, employing GOIA or FOCI pulses. Gradient spoilers of 10mT/m and 8 mT/m are used with 1.9 ms total duration (700 µs rampup/down times, 500 µs flat top) on all gradient channels. For MRSI the phase encoding gradients are superimposed on the last spoiler gradients. A minimum echo time TE of 45 ms and a repetition time TR of 1.5 s were used. A spectral window of 1.25 kHz (~10 ppm) and 1k points were used during acquisition.
In all adiabatic sequences the signal is excited initially with a non-selective adiabatic half passage (AHP) pulse based on offset independent adiabaticity HS8 [25] modulation with 4ms duration and a BW of 5 kHz (maximum RF amplitude 0.623 kHz).
Slice profiles and excitation uniformity in MRSI were measured in a uniform phantom that contains relevant brain metabolites at physiological concentrations. Signal localization and spectra quality were further tested in a multi-compartment phantom that contains oil and different brain metabolites. The measurements are performed also with the standard PRESS [22] sequence provided by Siemens, that uses Mao refocusing pulses [23] of 5.2 ms, BW of 1.17 kHz (R = 6) and peak RF amplitude of 1 kHz.
Pulses and sequences were last compared for in-vivo performance. MRSI brain spectra were collected on healthy volunteers (5 subjects). The studies with human subjects were approved by the IRB of our institution. Total acquisition times were 5.02 min for 2D MRSI with 20×16 elliptical phase encoding matrix and one average (NA = 1). The in-plane FOV was 20×16 cm2 (AP × RL), slice thickness of 1.5 cm, and the data matrix were interpolated to a 32×32 grid (a Hamming filter of width 50 was applied during reconstruction). Data were further analyzed using syngo VB15A or jMRUI3.0 software [30].
In the case of PRESS eight outer volume saturation (OVS) bands [31] were placed around the skull for lipid suppression. OVS was not used for LASER sequences. Water suppression was realized with a WET scheme [32]. A summary of parameters used in experiments and simulations are given in Table 1.
Table 1.
Parameters for RF pulses used in simulations and experiments
| RF pulse | B1 modulation | G modulationa | Tp (ms) | BW (kHz) | B1,max (kHz) |
|---|---|---|---|---|---|
| GOIA-W(16,4) | WURST-16 | WURST-4 | 3.5 | 20 | 0.817 |
| GOIA-HS(8,4) | HS8 | HS4 | 3.5 | 20 | 0.711 |
| FOCI | HS1 | C-shape | 3.5 | 20 | 1.463b |
| Mao | numerically optimized Sinc4 |
- | 5.2 | 1.17 | 1 |
a gradient factor f = 0.9 was used for all pulses;
for in-vivo MRSI measurements the maximum possible RF amplitude for FOCI was 1 kHz.
Images used to position MRSI in the case of volunteers were acquired with multi-echo MPRAGE (MEMPRAGE, TR = 2.53 s, TE1/TE2/TE2/TE3/TE4 = 1.64/3.5/5.36/7.22 ms, TI = 1.2 s, 1 mm isotropic resolution, Ref. [33]).
4. RESULTS
4.1 Slice profiles
Slice profiles have been simulated and measured experimentally at 3T for on-resonance (0 ppm chemical shift) and off-resonance (±1.75 ppm chemical shift) conditions. The performance was analyzed with regard to: i) flatness of the slices’ top, ii) sharpness of the slices’ edges, iii) CSDE in the presence of chemical shift, and iv) smearing artifacts for off-resonance slices. A slice of 2.5 cm thickness was assumed in both simulations and experiments.
GOIA (Eqs. 8–9) and FOCI (according to Ref. [14]) pulses of 3.5 ms and BW of 20 kHz were considered. The optimum RF amplitudes are: ii) 0.711 kHz for GOIA-HS(8,4), ii) 0.817 kHz GOIA-W(16,4), and iii) 1.463 kHz for FOCI. The peak amplitude of GOIA pulses is well below the 1 kHz upper limit of the RF amplitude delivered by the transmit body coil. In order to obtain the optimum 1.463 kHz RF amplitude for FOCI the safety monitor that limits maximum RF amplitude to 1 kHz had to be by-passed. However, for in-vivo measurements this is not possible.
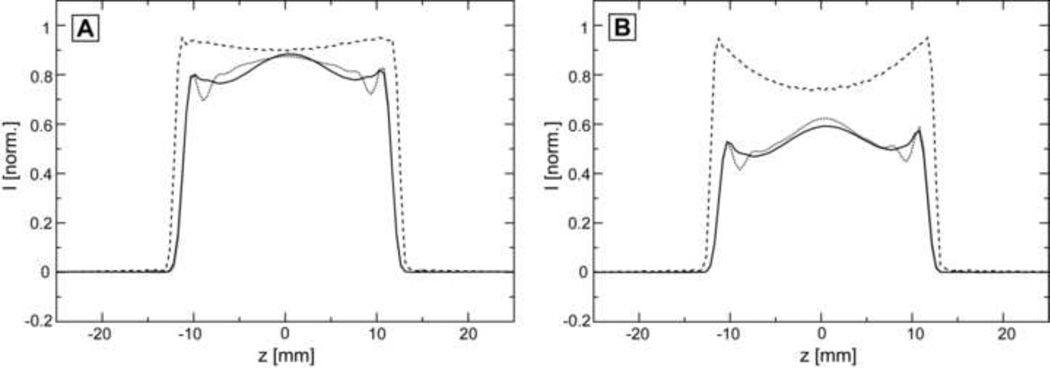
Figure 2A shows simulations of slice profiles in the absence of chemical shift and for optimal RF field. Flatness of the top is comparable for all three pulses in the center, however, GOIA-W(16,4) (solid line) seems to be better towards the edges of the top compared to GOIA-HS(8,4) (dotted line), but less than FOCI (dashed line). The signal drop-out around half maximum is similar for GOIA-W(16,4) and GOIA-HS(8,4), while FOCI have slightly sharper defined edges, as it is apparent from the wider slice profile towards the top. Figure 2B shows the measured slice profiles under the same conditions used in simulations. A good agreement with simulations is found. It is more apparent that FOCI (dashed line) has a slightly wider profile and sharper edges, than GOIA-W(16,4) (solid line) and GOIA-HS(8,4) (dotted line).
Figure 2.
Simulations and measurements of slice profiles for optimum RF amplitude at the isocenter in the absence of chemical shift: A) Simulations (overlaid) of slice profiles for pulses: GOIA-W(16,4) solid line, GOIA-HS(8,4) dotted line, and FOCI dashed line; B) Measured (overlaid) slice profile for pulses: GOIA-W(16,4) solid line, GOIA-HS(8,4) dotted line, and FOCI dashed line. Optimum RF amplitudes are: 0.817 kHz for GOIA-W(16,4), 0.711 kHz for GOIA-HS(8,4), and 1.463 kHz for FOCI.
Figure 3 presents the simulations and measurements of slice profiles in the presence of chemical shift. We consider a minimum of 3.5 ppm range for 1H chemical shift and the center frequency of the RF pulse set to the middle of this range. The slices for the right (+1.75 ppm, dotted line) and left (−1.75 ppm, dashed line) most shifted metabolites are compared with the on-resonance slice (0 ppm, solid line). Simulations are shown in the upper row: (A) GOIA-W(16,4), (B) GOIA-HS(8,4) and (C) FOCI. The “smearing” of the off-resonance (±1.75 ppm) slices caused by VERSE-ing the gradient, as originally described [11], is greatest in the case of GOIA-HS(8,4) (Fig. 3B). The slice smearing seems to be less for FOCI (Fig. 3C) than GOIA-W(16,4) (Fig. 3A). Less smearing is expected with FOCI since the gradient is modulated for a shorter period than the pulse duration (gradient is kept constant for a short period at the beginning and the end of pulse which makes it less susceptible to slice smearing but this also increases considerably the RF amplitude). The slices measured for the same offsets are in agreement with simulations and are shown in the lower row of: (D) GOIA-W(16,4), (E) GOIA-HS(8,4) and (F) FOCI.
Figure 3.
Simulations and measurements of slice profiles in the presence of chemical shift. A range of 3.5 ppm at 3T is considered. Slices for the extreme (−1.75/+1.75 ppm, dotted/dashed line) and center (0 ppm, solid line) chemical shifts are shown. Simulations: A) GOIA-W(16,4); B) GOIA-HS(8,4); C) FOCI. Measurements: D) GOIA-W(16,4); E) GOIA-HS(8,4); F) FOCI.
In the case of the FOCI pulse the optimum RF amplitude can not be reached in-vivo with the body coil, and Figure 4 compares the slice profiles measured for suboptimal RF amplitude for all three pulses (GOIA-W(16,4) solid line, GOIA-HS(8,4) dotted line, FOCI dashed line). In Figure 4A the amplitude is considered to be 70% from the optimal amplitude (1 kHz FOCI, 0.572 kHz GOIA-W(16,4), 0.497 kHz GOIA-HS(8,4)) and in Figure 4B the amplitude is reduced further to 50% from the optimum value (0.73 kHz FOCI, 0.408 kHz GOIA-W(16,4), 0.355 kHz GOIA-HS(8,4)). The intensity scale is normalized to the signal obtained with optimal RF amplitude. Two observations can be made: i) the FOCI pulse provides more signal for suboptimal RF amplitude compared to GOIA pulses, ii) however, the slice profile changes qualitatively more for FOCI (the middle of the slice profile degrades more than the edges) while GOIA pulses maintain a very similar aspect (especially GOIA-W(16,4)) as in the case of optimal RF amplitude (the slice profile at suboptimal RF amplitude is a scaled version of the one obtained with optimal RF amplitude for GOIA-W(16,4) but not for FOCI). The last aspect is explained by the fact that FOCI inverts earlier the edges of the slice compared to the center compared to GOIA that shows a more uniform response [13].
Figure 4.
Measured slice profiles for suboptimal RF amplitude: A) an RF amplitude of 70% from the optimal value is considered; B) an RF amplitude of 50% from the optimal value is considered. In both (A) and (B): GOIA-W(16,4) solid line, GOIA-HS(8,4) dotted line, and FOCI dashed line; the intensity scale is normalized to the signal obtained for optimal RF amplitude (Figure 2B).
4.2 Phantom spectra
Spectroscopic measurements have been performed by single voxel (SVS) and MRSI techniques with volume pre-selection using LASER [21] sequence for adiabatic pulses or PRESS [22] sequence for Mao [34] pulse.
Several aspects that have been investigated by 2D MRSI in a uniform phantom: i) CSDE, ii) excitation uniformity, iii) SNR, and iv) eddy currents artifacts. The accuracy of signal localization was checked with SVS in a multi-compartment phantom. Spectra of coupled spins were simulated and compared to SVS measurements in the case of Glutamate (Glu). Results are presented in Figure 5 for MRSI and Figure 6 for SVS.
Figure 5.
2D MRSI measurements in a uniform brain phantom. A large VOI (white rectangle) is selected with LASER or PRESS sequences and elliptical phase encoding is employed for signal localization inside the VOI. CSDE over a chemical range of 3.5 ppm is probed on the water signal in experiments without water suppression. Red dashed rectangle shows the CSDE in PRESS measurements. Spectral measurements are done with water suppression. NAA and Cho maps have the highest uniformity for GOIA-W(16,4) and FOCI pulses (red rectangles in PRESS indicate the CSDE). Spectra selected from the regions with the highest signal in the NAA maps show increased SNR for GOIA-W(16,4) and all the LASER spectra show considerable signal gain for coupled spins (Myo, Glu, Lac) compared to PRESS. Spectra shown in the bottom row present artifacts due to eddy currents for GOIA-HS(8,4) and FOCI (red arrows). The same acquisition parameters (TR = 1.5 s, TE = 45 ms, NA=1) are used in all measurements and the same intensity scale is chosen to display the results.
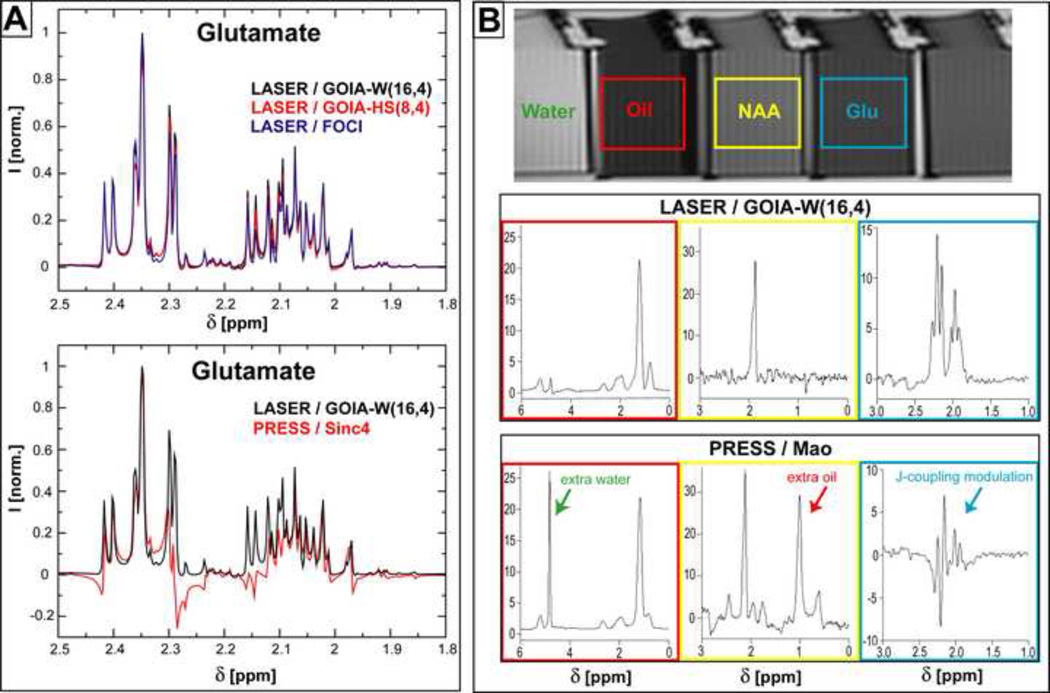
Figure 6.
Simulations of coupled spins spectra and SVS measurements in a multi-compartment phantom using LASER and PRESS sequences: A) Simulations of Glutamate spectra; B) single voxel spectra of Glutamate, NAA and Oil. The same TE (45 ms) and TR (1.5 s) are assumed throughout.
In Figure 5 the VOI (10×10 cm2) selected by LASER or PRESS is shown by the white square overlapped on phantom images. CSDE is evaluated by measuring the unsuppressed signal of water with pulses shifted −3.5 ppm from the water resonance. In the case of PRESS a large part of the VOI is shifted outside the boundaries of the VOI (the shift in the horizontal direction is smaller because it is selected by the initial 90° pulse in the PRESS sequence with different BW than the refocussing Mao pulse that selects the vertical direction, the red dashed rectangle indicate the size of VOI affected by CSDE). The excitation is well confined inside the VOI for adiabatic pulses, although the effects of slice smearing are visible for GOIA-HS(8,4).
Water suppressed MRSI or SVS is used in the following. The center frequency for VOI selection is set at 2.5 ppm in the middle of 4.3-0.8 ppm range. Uniformity of VOI excitation is shown in the NAA and Cho metabolite maps. GOIA-W(16,4) provides better uniformity for both chemical shifts. GOIA-HS(8,4) shows more slice smearing to increasing chemical shift offsets (NAA has −0.5 ppm offset from 2.5 ppm, Cho has +0.7 ppm offset from 2.5 ppm). FOCI pulses provide similar uniform excitation as GOIA-W(16,4), though a steeper drop-out of the signal towards the edges is apparent from the contour levels. PRESS excitation shows the largest non-uniformity with a large dip in the middle of VOI, especially along the horizontal (R-L) direction which is selected by the initial 90° pulse. The effects of CSDE are visible along the vertical (A-P) direction selected by the Mao pulse and indicated by the dashed red rectangles. The intensity is scaled the same in all the maps.
Examples of spectra from the same voxel chosen in a region of the NAA maps where all the data showed highest intensity are indicative of the SNR. There is a slight gain in SNR when using GOIA-W(16,4), followed by FOCI, GOIA-HS(8,4) and PRESS. All the LASER sequences show a significant SNR gain compared to PRESS in the case of coupled spins such as Myo-inositol (Myo), Glutamate (Glu) and Lactate (Lac). Few voxels in the center of VOI show signs of eddy currents artifacts which are largest for FOCI pulses, smaller for GOIA-HS(8,4), negligible for GOIA-W(16,4) and absent for PRESS. This is due to the slew rate which is greatest for FOCI (48.58 mT/m), smaller for GOIA-HS(8,4) (26.31 mT/m) and smallest for GOIA-W(16,4) (24.32 mT/m). Slew rates smaller than 25 mT/m seem to be recommended for spectra free of eddy currents artifacts when using the body gradient coil (TQ-engine) as the limit specified internally in the standard PRESS sequence from Siemens.
In Figure 6A simulated spectra of Glu are shown for LASER and PRESS sequences. The exact pulse shapes and time modulation from Figure 1 were considered in all cases. The spectral region span by Hβ (3CH2) and Hγ (4CH2) protons is shown enlarged. LASER spectra (Fig. 6A, upper part) show very little lineshape modulation due to J-coupling evolution at TE = 45 ms. An optimum SNR is predicted for GOIA-W(16,4) pulses. The effect of J-coupling evolution is visible as line modulation in PRESS spectra (Fig. 6A, lower part) for the same echo time.
Glutamate spectra are measured in a multi-compartment phantom which was used to test spectra localization. Separate compartments filled with Glu, NAA and oil, respectively, were placed in close contact in a larger container filled with water to reduce magnetic susceptibility anisotropy and help shimming. A phantom image and spectra obtained with LASER (GOIA-W(16,4)) and PRESS (Mao) are shown in Figure 6B. LASER provides in-phase absorption lineshapes for Glu, while an un-phasable mixture of absorption/dispersion lineshapes are obtained for Glu with PRESS at TE = 45 ms. In the case of NAA and oil spectra measured with PRESS a large contamination with external signal from the neighboring compartments can be noticed due to less sharp excitation profile.
4.3 MRSI of human brain
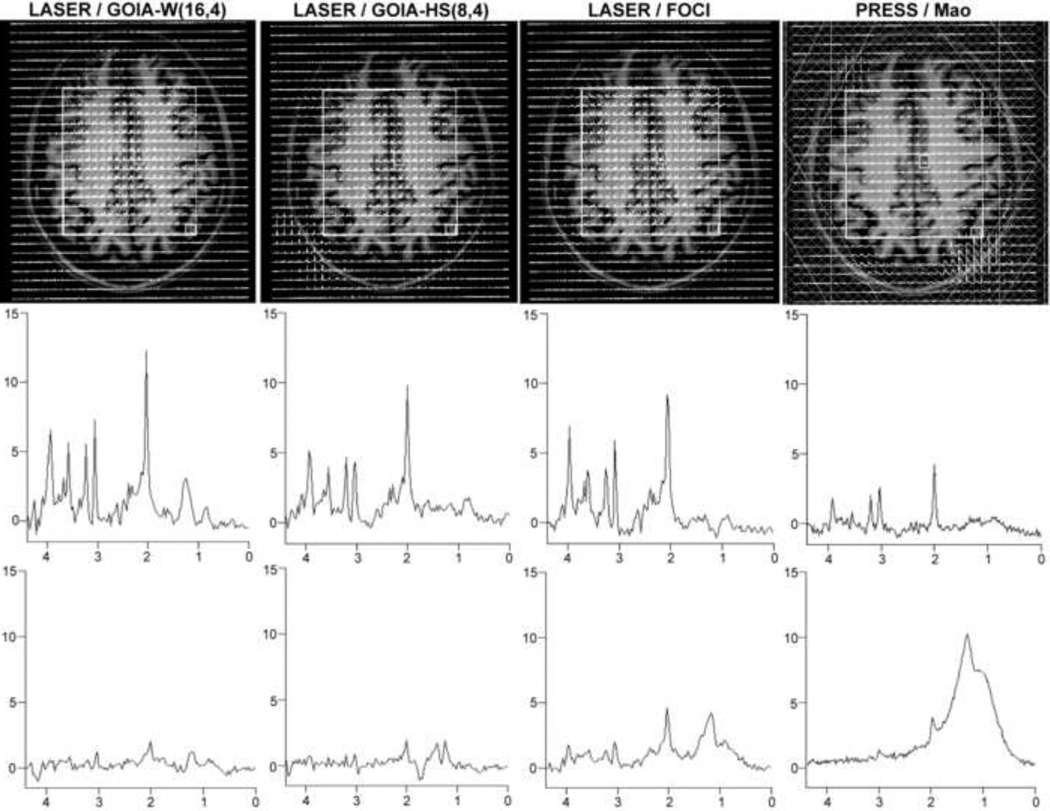
Representative data are shown from volunteers. 2D MRSI measured in a volunteer is shown in Figure 7. A large VOI (100×90 mm2, AP × RL, white rectangle) was positioned centrally in the brain above the ventricles (centrum semiovale) and parallel with the AC-PC (anterior-/posterior-comissure) line on the MEMPRAGE anatomical image. Large lipid contamination from the skull is visible in the posterior part of the VOI selected with PRESS despite the use of OVS bands (shown as hashed bands, top row). More posterior contamination is consistent also with the direction of CSDE for lipids. Spectra from a voxel situated in the lower right corner of VOI close to the skull shows the least lipid contamination for GOIA-W(16,4) pulse (bottom row). In the case of FOCI the intensity of lipid contamination is comparable with metabolite signals. Although the sharper slice profile of FOCI may provide more excitation towards the edges of the VOI this comes at the cost of increased excitation for subcutaneous lipids. Example of spectra from a centrally located voxel indicate the highest SNR for GOIA-W(16,4) (middle row). Results obtained so far in patients with brain tumors (glioblastoma multiforme) and stroke will be included in a separate manuscript.
Figure 7.
2D MRSI of brain in a volunteer obtained using LASER and PRESS sequences (TE = 45 ms, TR = 1.5 s). VOI is shown as the white rectangle. Top row: the matrix of spectra overlaid on the anatomical image (MEMPRAGE), for PRESS six OVS bands are used around the skull (shown as hashed bands). Middle row: example of spectra from a central voxel illustrates the SNR increase with GOIA-W(16,4). Lower row: example of spectra from a voxel situated in the corner of VOI (lower right corner) indicates the degree of lipid contamination, GOIA-W(16,4) shows the smallest lipid contamination.
5. DISCUSSIONS
Use of MRSI in routine clinical investigations has not grown to its full potential. Partly this is due to the fact that in many cases reliable data are not obtained and partly because traditionally MRSI requires long scanning time. Signal excitation and localization presents a series of challenges in MRSI. Data can be modified by a large number of artifacts (CSDE, lipid contamination, RF inhomogeneity) that increase with the main magnetic field. On the other hand higher B0 fields are needed for increased spectral dispersion.
Adiabatic pulses can reduce considerably these artifacts but often they are disregarded as being too long, too high SAR or too many (double the number of pulses are needed for refocusing). These imply increased echo times and long repetition times. VERSE design can help decrease SAR for adiabatic pulses. However, this is not enough in the case of FOCI pulses which still require impracticable high RF peak amplitude on typical clinical scanner equipped with only body transmit coil. Our work tries to address this problem by testing existing and new GOIA pulses that are more amenable in terms of RF power. Also, most clinical scanners are equipped only with whole-body gradient coils and eddy currents induced when large slew rates are involved in FOCI gradient modulation can influence spectral quality. This may explain why FOCI pulses demonstrated on research scanners equipped with dedicated head gradient inserts and transmit coils [14] are difficult to translate in clinical setup. A simpler approach to decrease the TE and also the SAR in the case of conventional adiabatic pulses has been to reduce the number of adiabatic pulses from six to four in semi-LASER sequence [9] by performing the initial excitation with a slice selective 90° (Sinc) pulse. This may not be optimal for transversal slices which are the most often used in brain MRSI, because it implies that the order of VOI selection starts with the transverse direction. It has been shown that it is optimum to start with the direction most affected by B0 inhomogeneity, the highest spectral quality for brain MRS being obtained for the sagital-coronal-transversal order [35].
We have proposed and tested a constant adiabaticity gradient modulated pulse (GOIA) starting from WURST waveforms that requires considerable less RF amplitude (40 %) and slew rates for the same specifications like the FOCI pulse. Although, the slices selected in the water phantom with FOCI have a better profile when optimum RF amplitude can be delivered, the GOIA-W(16,4) represents a good choice in-vivo leading to improved SNR, less lipid contamination and eddy current artifacts in the spectra, for greatly reduced B1 requirements. Reduced RF power enables shorter TR of 1.5 s (or less) to be used and reduce scanning time which is crucial in clinical conditions. Alternatively when TR is not limited, the peak amplitude of GOIA-W(16,4) pulse can be increased up to the maximum allowed by the clinical scanner in order to compensate more for the RF inhomogeneity. On the other hand, for suboptimal RF amplitude the slice profile of GOIA-W(16,4) is a scaled version of the profile obtained with optimum RF amplitude, making the correction in post-processing easier than in the case of FOCI where the middle of the slice changes more than the edges. However, at 3T excitation with the transmit body coil provides adequate RF homogeneity for brain imaging. Increase of RF amplitude can not be done for FOCI pulses which may require longer TR (6 s) due to SAR limitations. We found that GOIA-W(16,4) pulse has less slice smearing for off-resonance slices compared to GOIA pulses based on hyperbolic secant modulations (GOIA-HS(8,4)). This has been found to be true also when other GOIA-HS(m,n) were chosen. The RF amplitude for GOIA-W(16,4) is slightly higher (14.9%) than for GOIA-HS(8,4) but well within the limits of the transmit body coil. An increase in SNR is noticed with GOIA-W(16,4) vs. GOIA-W(8,4) or FOCI. The SNR gain is even more relevant compared to PRESS considering that the real VOI selected by PRESS is larger than the one excited with LASER (due to sharper slice profiles). As previously discussed [21], the relaxation under the LASER train of closely spaced adiabatic pulses is largely determined by T2ρ mechanisms which are more favorable than T2 relaxation in the PRESS sequence. Hence, there is less penalty for the longer minimum TE (45 ms) required by LASER (a minimum TE of 30 ms is possible in the standard PRESS sequence from Siemens). A significant gain is observed for spectra of coupled spins where the train of six adiabatic pulses acts also as a Carr-Purcell sequence that removes the effect of the J-coupling evolution on the lineshapes [21]. In-phase absorption lines of LASER can be better quantified than strongly modulated PRESS lines. These results are relevant for important metabolites involved in tumor (Myo), stroke (Lac) or healthy (Glu) conditions. Although shorter TE (~ 10 ms) are possible with PRESS which could give spectra with less J-coupling modulation [36,37], the TE can be shortened in LASER as well (TE ~ 20 ms), for example by reducing to half the BW (10 kHz) and pulse duration (1.5 ms) or skipping some gradient spoilers (such a sequence would still have better CSDE and RF uniformity than PRESS).
Improved signal localization with GOIA-W(16,4) translates into less lipid contamination from the subcutaneous fat that can leak into the VOI and dominate the metabolite spectra. This enables positioning of the VOI closer to the skull which in many clinical cases is required by the location of the lesion (tumor, stroke or other). The lipid OVS bands can be omitted and this helps to shorten the protocol setup time and regain (lower) some of the SAR. Moreover, it is very likely that imperfect OVS bands will perturb the magnetization inside VOI. Positioning of the OVS bands can be very subjective based on the operator experience and eliminating them could improve reliability. Due to spectral overlap, lipid contamination is most important in stroke where Lac can be an early marker of hypoxia.
A summary of performances for GOIA-W(16,4), GOIA-HS(8,4), FOCI, and Mao pulses in spectroscopic measurements is given in Table 2.
Table 2.
Summary of experimental performance in MRSI and SVS 3T measurements (except of the RF pulses, the same acquisition parameters were used, in particular TE = 45 ms and TR = 1.5s)
| RF pulse | CSDE | Uniformity of excitation |
Lipid contamination |
Eddy currents |
SNR | SAR (%)a |
|---|---|---|---|---|---|---|
| GOIA-W(16,4)b | +++ | +++ | − | − | ++++ | 72 |
| GOIA-HS(8,4)b | +++ | ++ | + | + | +++ | 55 |
| FOCIb | +++ | + | + | ++ | ++ | 100d |
| Maoc | − | − | ++++ | − | + | 20 |
percentage from the maximum allowed of 3W/kg, measured by the SAR watchdog monitor in the volunteer case;
LASER sequence;
PRESS sequence;
SAR for 1 kHz FOCI pulse. In the case of the optimal 1.463 kHz RF amplitude for FOCI the SAR would be 214 % (TR > 3 s would be necessary to reduce SAR below 100 %). Plus (+) and (−) symbols are given as a qualitative measure of the performance: i) for CSDE, uniformity of excitation and SNR the number of +/− is related to better/worse performance (ie. reduced CSDE and increased uniformity, which are the desired features, are specified by the number of +); ii) for lipid contamination and eddy currents the number of +/− relates to worse/better performance (ie. + means presence of lipids and eddy currents artifacts, which are not the desired features).
6. CONCLUSIONS
We have designed a new adiabatic pulse based on GOIA and WURST modulations. The new GOIA-W(16,4) pulse provides improved performance in MRSI applications compared to GOIA pulses based on hyperbolic secant functions (GOIA-HS(8,4)) or the FOCI pulse. We proved in phantoms and volunteers that GOIA-W(16,4) represents a good choice on standard 3T clinical scanners equipped with body transmit coil and body gradient coil due to a favorable combination of peak RF amplitude and slew rate requirements. We suggest that our method can increase the robustness and reliability of MRSI in clinical setup, and results that demonstrate this on clinical patients will be communicated in a future article. Improved MRSI is important especially in serial clinical studies (such as novel anti-angiogenic therapies for brain tumors [38]) where reliable data and reduced variability are required to detect treatment effects.
ACKNOWLEDGEMENTS
Funding from NIH, grant R01 1200-206456. Discussions with Drs. Thomas Benner and Andre van der Kouwe from Martinos Center, MGH, and Drs. Nouha Salibi, Mark Brown and Josef Pfeuffer from Siemens USA are gratefully acknowledged.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
REFERENCES
- 1.Brown TR, Kincaid BM, Ugurbil K. NMR Chemical-Shift Imaging in 3 Dimensions. Proceedings of the National Academy of Sciences of the United States of America-Biological Sciences. 1982;79(11):3523–3526. doi: 10.1073/pnas.79.11.3523. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Maudsley AA, Hilal SK, Perman WH, Simon HE. Spatially Resolved High-Resolution Spectroscopy by 4-Dimensional NMR. Journal of Magnetic Resonance. 1983;51(1):147–152. [Google Scholar]
- 3.Kurhanewicz J, Vigneron DB, Nelson SJ. Three-dimensional magnetic resonance spectroscopic imaging of brain and prostate cancer. Neoplasia. 2000;2(1–2):166–189. doi: 10.1038/sj.neo.7900081. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Barker PB, Gillard JH, Vanzijl PCM, et al. Acute Stroke - Evaluation with Serial Proton Mr Spectroscopic Imaging. Radiology. 1994;192(3):723–732. doi: 10.1148/radiology.192.3.8058940. [DOI] [PubMed] [Google Scholar]
- 5.Stanley JA. In vivo magnetic resonance spectroscopy and its application to neuropsychiatric disorders. Canadian Journal of Psychiatry-Revue Canadienne De Psychiatrie. 2002;47(4):315–326. doi: 10.1177/070674370204700402. [DOI] [PubMed] [Google Scholar]
- 6.Silver MS, Joseph RI, Hoult DI. Selective Spin Inversion in Nuclear Magnetic-Resonance and Coherent Optics through an Exact Solution of the Bloch-Riccati Equation. Physical Review A. 1985;31(4):2753–2755. doi: 10.1103/physreva.31.2753. [DOI] [PubMed] [Google Scholar]
- 7.Baum J, Tycko R, Pines A. Broad-Band and Adiabatic Inversion of a 2-Level System by Phase-Modulated Pulses. Physical Review A. 1985;32(6):3435–3447. doi: 10.1103/physreva.32.3435. [DOI] [PubMed] [Google Scholar]
- 8.Conolly S, Nishimura D, Macovski A. A Selective Adiabatic Spin-Echo Pulse. Journal of Magnetic Resonance. 1989;83(2):324–334. doi: 10.1002/mrm.1910180105. [DOI] [PubMed] [Google Scholar]
- 9.Scheenen TWJ, Klomp DWJ, Wijnen JP, Heerschap A. Short echo time H-1-MRSI of the human brain at 3T with minimal chemical shift displacement errors using adiabatic refocusing pulses. Magnetic Resonance in Medicine. 2008;59(1):1–6. doi: 10.1002/mrm.21302. [DOI] [PubMed] [Google Scholar]
- 10.Conolly S, Glover G, Nishimura D, Macovski A. A Reduced Power Selective Adiabatic Spin-Echo Pulse Sequence. Magnetic Resonance in Medicine. 1991;18(1):28–38. doi: 10.1002/mrm.1910180105. [DOI] [PubMed] [Google Scholar]
- 11.Conolly S, Nishimura D, Macovski A, Glover G. Variable-Rate Selective Excitation. Journal of Magnetic Resonance. 1988;78(3):440–458. [Google Scholar]
- 12.Ordidge RJ, Wylezinska M, Hugg JW, Butterworth E, Franconi F. Frequency offset corrected inversion (FOCI) pulses for use in localized spectroscopy. Magnetic Resonance in Medicine. 1996;36(4):562–566. doi: 10.1002/mrm.1910360410. [DOI] [PubMed] [Google Scholar]
- 13.Tannus A, Garwood M. Adiabatic pulses. NMR in Biomedicine. 1997;10(8):423–434. doi: 10.1002/(sici)1099-1492(199712)10:8<423::aid-nbm488>3.0.co;2-x. [DOI] [PubMed] [Google Scholar]
- 14.Kinchesh P, Ordidge RJ. Spin-echo MRS in humans at high field: LASER localisation using FOCI pulses. Journal of Magnetic Resonance. 2005;175(1):30–43. doi: 10.1016/j.jmr.2005.03.009. [DOI] [PubMed] [Google Scholar]
- 15.Sacolick LI, Rothman DL, de Graaf RA. Adiabatic refocusing pulses for volume selection in magnetic resonance spectroscopic imaging. Magnetic Resonance in Medicine. 2007;57(3):548–553. doi: 10.1002/mrm.21162. [DOI] [PubMed] [Google Scholar]
- 16.Near J, Romagnoli C, Curtis AT, et al. High-Field MRSI of the Prostate Using a Trasnmit/Receive Endorectal Coil and Gradient Modulated Adiabatic Localization. Journal of Magnetic Resonance Imaging. 2009;30(2):335–345. doi: 10.1002/jmri.21841. [DOI] [PubMed] [Google Scholar]
- 17.Andronesi OC, Ramadan S, Ratai EM, Jennings D, Mountford CE, Sorensen AG. Gradient offset independent adiabatic pulses for high-field MR spectroscopy on clinical scanners. In the Proceedings of the 17th ISMRM Meeting; Hawaii. 2009. #332. [Google Scholar]
- 18.Kupce E, Freeman R. Adiabatic Pulses for Wide-Band Inversion and Broad-Band Decoupling. Journal of Magnetic Resonance Series A. 1995;115(2):273–276. [Google Scholar]
- 19.Setsompop K, Wald LL, Alagappan V, et al. Parallel RF transmission with eight channels at 3 Tesla. Magnetic Resonance in Medicine. 2006;56(5):1163–1171. doi: 10.1002/mrm.21042. [DOI] [PubMed] [Google Scholar]
- 20.Setsompop K, Alagappan V, Gagoski B, et al. Slice-Selective RF Pulses for In Vivo B-1(+) Inhomogeneity Mitigation at 7 Tesla Using Parallel RF Excitation With a 16-Element Coil. Magnetic Resonance in Medicine. 2008;60(6):1422–1432. doi: 10.1002/mrm.21739. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Garwood M, DelaBarre L. The return of the frequency sweep: Designing adiabatic pulses for contemporary NMR. Journal of Magnetic Resonance. 2001;153(2):155–177. doi: 10.1006/jmre.2001.2340. [DOI] [PubMed] [Google Scholar]
- 22.Bottomley PA. Spatial Localization in NMR-Spectroscopy Invivo. Annals of the New York Academy of Sciences. 1987;508:333–348. doi: 10.1111/j.1749-6632.1987.tb32915.x. [DOI] [PubMed] [Google Scholar]
- 23.Mao J, Mareci TH, Andrew ER. Experimental-Study of Optimal Selective 180-Degrees Radiofrequency Pulses. Journal of Magnetic Resonance. 1988;79(1):1–10. [Google Scholar]
- 24.Jung WI, Bunse M, Lutz O. Quantitative evaluation of the lactate signal loss and its spatial dependence in PRESS localized H-1 NMR spectroscopy. Journal of Magnetic Resonance. 2001;152(2):203–213. doi: 10.1006/jmre.2001.2420. [DOI] [PubMed] [Google Scholar]
- 25.Tannus A, Garwood M. Improved performance of frequency-swept pulses using offset-independent adiabaticity. Journal of Magnetic Resonance Series A. 1996;120(1):133–137. [Google Scholar]
- 26.Ernst RR, Bodenhausen G, Wokaun A. In: Principles of Nuclear Magnetic Resonance in One and Two Dimensions. Halpern J, Green MLH, T M, editors. Oxford: Clarendon Press; 1987. [Google Scholar]
- 27.Haeberlen U. Selective averaging. In: Waugh JS, editor. Advances in Magnetic Resonance, High resolution NMR in solids. Academic Press; 1976. [Google Scholar]
- 28.Smith SA, Levante TO, Meier BH, Ernst RR. Computer-Simulations in Magnetic-Resonance - an Object-Oriented Programming Approach. Journal of Magnetic Resonance Series A. 1994;106(1):75–105. [Google Scholar]
- 29.Govindaraju V, Young K, Maudsley AA. Proton NMR chemical shifts and coupling constants for brain metabolites. NMR in Biomedicine. 2000;13(3):129–153. doi: 10.1002/1099-1492(200005)13:3<129::aid-nbm619>3.0.co;2-v. [DOI] [PubMed] [Google Scholar]
- 30.Naressi A, Couturier C, Devos JM, et al. Java-based graphical user interface for the MRUI quantitation package. Magnetic Resonance Materials in Physics Biology and Medicine. 2001;12(2–3):141–152. doi: 10.1007/BF02668096. [DOI] [PubMed] [Google Scholar]
- 31.Moonen CTW, Sobering G, Vanzijl PCM, Gillen J, Vonkienlin M, Bizzi A. Proton Spectroscopic Imaging of Human Brain. Journal of Magnetic Resonance. 1992;98(3):556–575. [Google Scholar]
- 32.Ogg RJ, Kingsley PB, Taylor JS. Wet, a T-1-Insensitive and B-1-Insensitive Water-Suppression Method for in-Vivo Localized H-1-NMR Spectroscopy. Journal of Magnetic Resonance Series B. 1994;104(1):1–10. doi: 10.1006/jmrb.1994.1048. [DOI] [PubMed] [Google Scholar]
- 33.van der Kouwe AJW, Benner T, Salat DH, Fischl B. Brain morphometry with multiecho MPRAGE. Neuroimage. 2008;40(2):559–569. doi: 10.1016/j.neuroimage.2007.12.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Mao JT, Mareci TH, Scott KN, Andrew ER. Selective Inversion Radiofrequency Pulses by Optimal-Control. Journal of Magnetic Resonance. 1986;70(2):310–318. [Google Scholar]
- 35.Ernst T, Chang L. Elimination of artifacts in short echo time H-1 MR spectroscopy of the frontal lobe. Magnetic Resonance in Medicine. 1996;36(3):462–468. doi: 10.1002/mrm.1910360320. [DOI] [PubMed] [Google Scholar]
- 36.Zhong K, Ernst T. Localized in vivo human H-1 MRS at very short echo times. Magnetic Resonance in Medicine. 2004;52(4):898–901. doi: 10.1002/mrm.20201. [DOI] [PubMed] [Google Scholar]
- 37.Mekle R, Mlynarik V, Gambarota G, Hergt M, Krueger G, Gruetter R. MR Spectroscopy of the Human Brain With Enhanced Singla Intensity at Ultrashort Echo Times on a Clinical Platform at 3T and 7T. Magnetic Resonance in Medicine. 2009;61(6):1279–1285. doi: 10.1002/mrm.21961. [DOI] [PubMed] [Google Scholar]
- 38.Batchelor TT, Sorensen AG, di Tomaso E, et al. AZD2171, a pan-VEGF receptor tyrosine kinase inhibitor, normalizes tumor vasculature and alleviates edema in glioblastoma patients. Cancer Cell. 2007;11(1):83–95. doi: 10.1016/j.ccr.2006.11.021. [DOI] [PMC free article] [PubMed] [Google Scholar]