Location via proxy:   [ UP ]  
[Report a bug]   [Manage cookies]                
Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2015 May 5.
Published in final edited form as: Neuroimage. 2013 Nov 5;88:22–31. doi: 10.1016/j.neuroimage.2013.09.034

Real-time motion- and B0-correction for LASER-localized spiral-accelerated 3D-MRSI of the brain at 3T

Wolfgang Bogner 1,2,*, Aaron T Hess 3, Borjan Gagoski 4, M Dylan Tisdall 1, Andre JW van der Kouwe 1, Siegfried Trattnig 2, Bruce Rosen 1, Ovidiu C Andronesi 1,#
PMCID: PMC4010560  NIHMSID: NIHMS537933  PMID: 24201013

Abstract

The full potential of magnetic resonance spectroscopic imaging (MRSI) is often limited by localization artifacts, motion-related artifacts, scanner instabilities, and long measurement times.

Localized adiabatic selective refocusing (LASER) provides accurate B1-insensitive spatial excitation even at high magnetic fields. Spiral encoding accelerates MRSI acquisition, and thus, enables 3D-coverage without compromising spatial resolution. Real-time position-and shim/frequency-tracking using MR navigators correct motion- and scanner instability-related artifacts. Each of these three advanced MRI techniques provides superior MRSI data compared to commonly used methods.

In this work, we integrated in a single pulse sequence these three promising approaches. Real-time correction of motion, shim, and frequency-drifts using volumetric dual-contrast echo planar imaging-based navigators were implemented in an MRSI sequence that uses low-power gradient modulated short-echo time LASER localization and time efficient spiral readouts, in order to provide fast and robust 3D-MRSI in the human brain at 3T.

The proposed sequence was demonstrated to be insensitive to motion- and scanner drift-related degradations of MRSI data in both phantoms and volunteers. Motion and scanner drift artifacts were eliminated and excellent spectral quality was recovered in the presence of strong movement.

Our results confirm the expected benefits of combining a spiral 3D-LASER-MRSI sequence with real-time correction. The new sequence provides accurate, fast, and robust 3D metabolic imaging of the human brain at 3T. This will further facilitate the use of 3D-MRSI for neuroscience and clinical applications.

Keywords: magnetic resonance spectroscopy, LASER localization, prospective motion correction, real-time correction, spiral acceleration, frequency drift correction

1. Introduction

Magnetic resonance spectroscopic imaging (MRSI) is a powerful noninvasive tool for the study of spatially heterogeneous biochemical changes that underlie many brain pathologies. Similar to other MRI techniques, robust imaging with high spatial resolution and 3D coverage of the pathologic region is desired, but, in practice, technical and physiological limitations make trade-offs for MRSI necessary (Duarte et al., 2012).

High-field (≥3T) MRSI offers high spectral quality (Tkac et al., 2009) and spatial resolution (Bogner et al., 2012), but is limited by: 1) localization artifacts due to imperfect selection profiles, chemical shift errors, and B1 inhomogeneities (Andronesi et al., 2010; Kreis, 2004; Scheenen et al., 2008); 2) motion-related artifacts caused by position changes, phase artifacts, B0 changes, and lipid contamination (Hess et al., 2011; Kreis, 2004); 3) scanner instabilities, such as those resulting from heating of gradient coil and passive shims, that cause slow B0 drift (Ebel and Maudsley, 2005; El-Sharkawy et al., 2006); and 4) long measurement times, which limit spatial coverage and resolution (Adalsteinsson et al., 1998; Ebel and Maudsley, 2005; Posse et al., 1995). This can make common metabolic assessments by 3D-MRSI, in particular, inaccurate, error-prone, and slow.

Previous reports have validated the improved spatial selection accuracy of localized adiabatic selective refocusing (LASER) at high fields (Andronesi et al., 2010; Garwood and DelaBarre, 2001; Scheenen et al., 2008). Spiral encoding or echo planar spectroscopic imaging (EPSI, PEPSI) accelerate MRSI acquisitions and, thus, enable 3D coverage with high spatial resolution in clinically feasible measurement times (Adalsteinsson et al., 1998; Andronesi et al., 2012; Maudsley et al., 2009; Posse et al., 1995). The efficient combination of both acceleration and accurate selection has been recently shown to have a significant clinical impact (Andronesi et al., 2012).

Long scan times make standard 3D-MRSI particularly susceptible to motion-induced artifacts. Unlike the case with conventional imaging techniques, these artifacts cannot be easily recognized and, thus, may bias clinical diagnoses (Kreis, 2004). On the one hand, reducing measurement times by accelerated acquisition (i.e., spirals, EPSI) makes motion artifacts less likely (Kim et al., 2004), but not impossible. On the other hand, a heavy duty cycle, such as that used for EPSI and spirals, may result in temporal B0 changes caused by heating of the gradient coils and passive shims, in addition to inevitable B0 field drifts caused by instabilities of the superconducting magnet (Ebel and Maudsley, 2005; El-Sharkawy et al., 2006). Therefore, adequate motion and B0 correction is essential.

Several studies have reported significantly improved spectral quality for both single-voxel spectroscopy (SVS) and 2D-MRSI, when retrospective, prospective, or a combination of both motion corrections is used (Andrews-Shigaki et al., 2011; Boer et al., 2012; de Nijs et al., 2009; Ernst and Li, 2011; Hess et al., 2012; Hess et al., 2011; Keating and Ernst, 2012; Lange et al., 2012; Lin et al., 2009; Thiel et al., 2002; Zaitsev et al., 2010). While retrospective correction alone (e.g., frequency/phase alignment of separately saved averages) can improve data quality to a certain degree (Helms and Piringer, 2001; Kim et al., 2004; Posse et al., 1993), prospective real-time motion correction (i.e., updating the MR sequence in real-time) can further improve data quality (Andrews-Shigaki et al., 2011; Hess et al., 2012; Hess et al., 2011; Lange et al., 2012; Zaitsev et al., 2010).

Prospective motion correction detects motion before each excitation, once per repetition time (TR), and performs any relevant corrections within the same TR. A comprehensive prospective correction includes : 1)a real-time position update of the imaging volume (i.e., the imaging volume “follows” the object), 2) a B0 shim update (i.e., dynamic shimming), 3) and an RF carrier frequency update (Maclaren et al., 2012).

There are three conceptually different real-time motion-tracking approaches that can be used for prospective correction: 1) optical tracking (Andrews-Shigaki et al., 2011; Lange et al., 2012; Zaitsev et al., 2010); 2) active markers (Ooi et al., 2009); and 3) MR navigators (Hess et al., 2012; Hess et al., 2011; Thiel et al., 2002). To date, only optical tracking and MR navigators have been used for MRS motion correction. Optical tracking requires no changes to pulse sequence timing, but needs additional external hardware and calibration. Without additional sequence changes, only volume of interest (VOI) correction is possible, but with no updating of shims or frequency. On the other hand, MR navigators require no additional hardware, but may prolong the TR of some MR sequences. This is the reason why MR navigators are particularly suitable for MR sequences that already require long TR and have sequence dead times between signal readout and the subsequent excitation. MRS sequences or MRI sequences with inversion recovery preparation fulfill both criteria, and are, therefore, not limited by the use of MR navigators (Hess et al., 2012; Hess et al., 2011; Keating and Ernst, 2012; Maclaren et al., 2012; Tisdall et al., 2012). Even complicated navigators can be easily placed inside the dead time of an MRSI sequence, without restricting minimum TR (Hess et al., 2012; Hess et al., 2011).

Recently employed navigator approaches include k-space navigators, such as cloverleaf navigators (van der Kouwe et al., 2006), orbital navigators (Fu et al., 1995), or spherical navigators (Welch et al., 2002), and image-based navigators, such as PROMO (Keating and Ernst, 2012; White et al., 2010) or echo planar imaging navigators (Hess et al., 2012; Hess et al., 2011; Tisdall et al., 2012).

Volumetric navigators (vNav), based on 3D dual-contrast multi-shot EPI, rapidly generate two low-resolution 3D images before each excitation (Hess et al., 2012; Hess et al., 2011; Tisdall et al., 2012). These crude anatomical images can be registered to a reference volume to extract sub-millimeter position updates. Using both contrasts, 3D B0-field maps can be generated to update relevant shim adjustment terms and frequency.

The aim of our study was, to implement a new 3D-MRSI sequence that integrates the benefits of spiral-accelerated, LASER-localized 3D-MRSI with real-time corrections for motion-, shim-, and frequency drifts (ShMoCo) using vNav. This new sequence was evaluated in phantoms and volunteers at 3T and should provide fast and robust volumetric metabolic imaging of the human brain.

2. Materials and Methods

2.1. Sequence design and motion correction

2.1.1. Spatial localization

VOI localization in our 3D-MRSI measurements was achieved by a B1-insensitive LASER sequence (Andronesi et al., 2012; Andronesi et al., 2010; Garwood and DelaBarre, 2001). Excitation was performed by a non-selective adiabatic half passage pulse (HS8 modulation; duration 4 ms; bandwidth 5 kHz). Three pairs of Gradient Offset Independent Adiabatic (GOIA) pulses (W16,4 modulation; 3.5 ms duration and 20 kHz bandwidth) guaranteed accurate LASER localization with low power requirements and negligible chemical shift displacement errors (Andronesi et al., 2010; Tannus and Garwood, 1997). A minimum echo time (TE) of 27 ms can be achieved by eliminating spoilers for the first five GOIA pulses. Our data were acquired with a TE of 30 ms to allow comparison with the bulk of the MRSI papers that use PRESS excitation.

Time efficient data acquisition was achieved by spiral encoding in the (kx,ky)-plane using constant-density spiral trajectories (Adalsteinsson et al., 1998). Gradient delays of 8 μs between the ADC and the X and Y gradients were measured, and corrected for in the reconstruction. Phase encoding gradients were superimposed over the last Z-spoiler gradient of the LASER sequence to encode along the z direction. This resulted in a cylindrical 3D-coverage of the k-space by a stack of spirals.

2.1.2. Volumetric navigator

For the detection of real-time motion and B0-field distortion a dual-contrast, multi-shot 3D-EPI navigator was inserted prior to the water suppression module of the 3D-MRSI sequence. This vNav determined the required shim, frequency, and head pose changes (if any) once per TR, and allowed corrections within the same TR. The vNav protocol parameters selected for this study were: TR 17 ms; TE1/TE2 7/9.4 ms; matrix 32×32; 18 slices; FOV 256×256×144 mm3; 8 mm isotropic resolution; bandwidth 3906 Hz/pixel; flip angle 2°. The small flip angle does not observably affect the spins available for excitation (Hess et al., 2011). The two imaging contrasts (i.e., TE1/TE2) were generated with interleaved partition acquisitions. Additional reference k-space lines for N/2-ghosting correction were measured. The total navigator duration was 612 ms. The navigator was positioned over the subject’s brain using a “setter” sequence that was run prior to the 3D-MRSI sequence adjustment. Besides positioning, the “setter” sequence allows definition of all important vNav sequence parameters including TR, TE1/TE2, flip angle, FOV, slices, matrix size, readout bandwidth, and echo spacing. This “setter” sequence takes only one second and adjusts the protocol parameters of the vNav that is subsequently run inside the 3D-MRSI sequence.

For each TR, pose changes are computed online by co-registering the magnitude image (i.e., the first TE1 contrast) of the current vNav (Figure 1) to the initial vNav, using PACE (Prospective Acquisition Correction) (Thesen et al., 2000). This information was used to update all imaging gradients and RF pulses responsible for VOI and FOV positioning. In addition, field maps (Figure 1) were reconstructed from phase maps of both contrasts using PRELUDE (Phase Region Expanding Labeller for Unwrapping Discrete Estimates) (Jenkinson, 2003). Two sets of zero-/first-/second-order shim terms were calculated online, one for the MRSI VOI and one for the navigator FOV. The shim estimate for the navigator was calculated using an unweighted least squares regression. The shim estimate for the VOI used a weighted least squares regression, where the weighting of each navigator voxel is according to its intersection with the VOI. Only zero- and first-order shim terms were applied. Second-order shim terms were obtained, but could not be updated with available hardware. All online calculations were performed in less than 150 ms. Thus, the total block, including navigator acquisition (612 ms) and online processing (150 ms), takes ~760 ms. Navigator acquisition, updating, and all of the image reconstruction was fully implemented and integrated on the scanner.

Figure 1.

Figure 1

Open in a new tab

Sample images obtained by the volumetric EPI navigator: (a) Magnitude images for the first contrast (i.e., TE1) were used for position change calculations and (b) corresponding masked field maps derived from both contrasts were used to update frequency and first-order shim terms.

2.1.3. Real-time sequence updating

When moving a VOI that is determined by gradient-modulated pulses, simply adding a constant frequency offset for the selective pulses is not sufficient. For gradient-modulated pulses (e.g., GOIA), the total phase modulation ϕtotal that determines slice thickness and position has a slice-offset Z-dependent component, ϕoff, and an offset-independent component, ϕiso. For real-time changes in position offset z, only the gradient-modulated G(τ) and z-dependent ϕoff has to be updated each TR:

ϕtotal(z,t)=ϕiso(t)+ϕoff(z,t)=ϕiso+2π∫0tγzG(τ)·dτ (Eq.1)

For FOV readjustments, phase encoding and spiral encoding were updated independently. Phase encoding in the z-direction was updated by adding a constant excitation phase roll during sequence run-time to account for translation as traditionally performed for off-center MRSI scans.

Offsets in the spiral-encoded directions, i.e. in the (kx,ky)-plane cannot be corrected for using a constant phase roll, because of non-cartesian k-space sampling. Therefore, motion in the x/y-plane is corrected for during online image reconstruction by adding a corresponding phase roll in the x- and y-directions before gridding and combination of the different temporal and angular interleaves.

Real-time rotations updates were implemented by rotating the phase encoding and spiral encoding gradients per vNav output. The reference frequency and phase of the excitation pulse, refocusing pulses, water suppression pulses, and ADC readout were updated according to the vNav. Shim updating was performed during each TR prior to water suppression.

2.2. Scanner hardware

All in vivo measurements were performed on a 3T TIM Trio MR scanner (Siemens Healthcare, Erlangen, Germany) using the body coil for transmission and a standard 12-channel head coil (Siemens Healthcare, Erlangen, Germany) for signal reception. Localization phantom measurements were performed using the body coil for signal reception and transmission, to allow the simulation of large translations (i.e., up to 10 cm).

2.3. Phantoms

For localization and frequency drift tests, two different phantoms were used. The first phantom was a cylindrical, multi-compartment phantom that contained water and three tubes, each filled with a chemical compound of different spectral appearance (i.e., acetate, ethanol, and isopropyl alcohol) and with similar concentrations. Different amounts of Gd-DPTA (Magnevist) were used to reduce overall T1 relaxation times and to enable good visual differentiation of the three tubes and surrounding water (Figures 2–5). The second phantom was a spherical spectroscopy phantom (i.e., containing brain metabolites).

Figure 2.

Figure 2

Open in a new tab

Localization experiment in a cylindrical multi-compartment phantom probing (a) translation of the phantom by 5 cm, relative to the FOV (white square), in the right-left (spiral-encoded in-plane) direction. In (b), the static case spectra of all three chemical compounds are localized well within their tubes, while in (c) translation led to both decreased spectral quality and severe localization errors. Both sources of error were eliminated by ShMoCo, and (d) localization accuracy and spectral quality were recovered. The white arrow illustrates the direction of movement.

2.3.1. Localization correction

The accuracy of the implemented prospective ShMoCo was verified using the multi-compartment phantom by performing different kinds of movement, which included translation of at most 5–8 cm, and rotations between 30°–45° (note: the maximum possible movement is limited by the registration algorithm to 8° rotation and 2 cm translation per TR). To investigate the accurate correction for both rotation and translation in phase-encoded and spiral-encoded directions, the following standardized movement patterns were performed: (a) right-left (spiral-encoded in-plane) translation; (b) head-feet (phase-encoded through-plane) translation; (c) transversal (spiral-encoded in-plane) rotation; and (d) coronal (phase/spiral-encoded through-plane) rotation (Figures 2–5).

For each movement pattern, four measurements were performed and compared: 1) one static measurement without ShMoCo; 2) one static measurement with ShMoCo; 3) one motion-degraded measurement without ShMoCo; and 4) one motion-degraded measurement with ShMoCo during the acquisition.

The following measurement parameters were used for phantom testing: TR/TE 1500/30 ms; 0.25cc isotropic voxels; 32×32×16 matrix; no interpolation; FOV 200×200×100 mm3; VOI 120×120×60 mm3; spectral acquisition bandwidth 1.25 kHz; two temporal and ten angular interleaves; one average; four preparation scans; no water suppression; TA 8:08 min. An automated gradient echo imaging-based shimming routine was used to set the initial B0 shim.

2.3.2. Scanner frequency drift/B0 correction

Frequency drift during a 3D-MRSI scan with standard-resolution in a static spherical brain metabolite phantom was assessed using the following 3D-MRSI protocol: TR/TE 1600/30 ms; 20×20×12 matrix; FOV 200×200×120 mm3; VOI 80×80×80 mm3; spectral acquisition bandwidth 1.25 kHz; two temporal and four angular interleaves; eight averages; TA 20:35 min.

2.4. 3D-MRSI of human subjects

For in vivo validation, four measurement sessions were performed on three healthy volunteers (two males, one female; age, 31±1years). Institutional Review Board approval and written, informed consent was obtained. For all three volunteers, standard-resolution scans (i.e., 20×20×12 matrix with 1cc isotropic resolution) were performed with moderate motion. In addition, one volunteer was also measured a second time using longer high-resolution scans (i.e., 25×25×12 matrix with 0.5cc isotropic resolution) with more severe motion.

Each in vivo measurement session began with a structural MEMPRAGE sequence (van der Kouwe et al., 2008) to guide initial VOI localization. To save measurement time, only the most likely motion patterns for in vivo situations were performed (i.e., right-left head rotation, chin up-down rotation, head-feet translation). The motion patterns were kept simple to ensure good reproducibility.

After each motion-degraded experiment, the volunteers were instructed to return to their original position. Localizer images were repeatedly acquired to validate that the subjects had indeed returned to their initial position. To further ensure the reproducibility of initial head position relative to the VOI/FOV adjustment, AutoAlign was run prior to each MRSI scan (Benner et al., 2006; van der Kouwe et al., 2005). Gradient echo imaging based shimming was repeated after each motion scan to set the initial B0 shim. All subjects were briefed and trained in a short test session prior to the actual movement experiments. For standard resolution MRSI, the volunteers were instructed to move their head slowly over a time span of one minute per motion task. and there was only one type of motion task tested during a given scan. For the high resolution MRSI scan, all three motion tasks were performed during the same scan, each task for one minute separated by equally spaced static periods. An audio cue was given at the start and end of each movement subtask.

2.4.1. Short standard-resolution scan – moderate motion

All volunteers performed a total of eight scans. This included four sets of experiments with each set focusing on one of four specific (motion) tasks (i.e., static case, right-left head rotation by 22±3°, chin up-down rotation by 14±2°, head-feet translation by 20±2 mm). Each set consisted of two measurements: one with and one without ShMoCo. Excluding training and instructions, each measurement session was ~70–90 min long.

The following in vivo 3D-MRSI sequence parameters were used: TR/TE 1600/30 ms; 1cc isotropic voxels; 20×20×12 matrix interpolated to a 32×32×16 matrix; FOV 200×200×120 mm3; VOI 110×90×50 mm3; bandwidth 1.25 kHz; two temporal and four angular interleaves; two averages; four preparation scans; TA 5:14 min.

2.4.2. Long high-resolution scan – severe motion

One volunteer also performed three longer measurements. As there was no difference expected between static high-resolution scans with and without ShMoCo based on the previously evaluated standard-resolution scans as well as previous reports (Hess et al., 2012; Hess et al., 2011) and to shorten the total measurement protocol, only one static scan was performed. Thus, there was one static and two complex motion tasks (i.e., combination of right-left head rotation by 20°, chin up-down rotation by 14°, and head-feet translation by 20 mm)(Figure 6).

Figure 6.

Figure 6

Open in a new tab

(a) Translation, (b) rotation, (c) first-order shim terms, and (d) frequency changes, as measured by the vNav during the high-resolution 3D-MRSI scan are plotted as a function of measurement time in the scanner coordinate system. During the ~15min scan, three different motion tasks were performed by the volunteer, with three-minute gaps between the tasks in the following order: head-feet translation by 22 mm; right-left head rotation by 19°; and chin up-down rotation by 12°. The frequency drifts observed due to scanner instabilities during the corresponding static scan are depicted in (d), shoulder-to-shoulder with the frequency changes observed during the motion-affected scan.

The following in vivo 3D-MRSI sequence parameters were used: TR/TE 1600/30 ms; 0.5cc isotropic voxels; 25×25×12 matrix interpolated to a 32×32×16 matrix; FOV 200×200×96 mm3; VOI 110×88×50 mm3; bandwidth 1.25 kHz; two temporal and six angular interleaves; four averages; four preparation scans; TA 15:28 min.

2.5. Data evaluation and statistical analysis

Statistical analysis was performed and plots were created using SPSS (v15.0; Chicago, Ill).

Localization accuracy and spectral quality were evaluated qualitatively (i.e., visual assessment of spectral quality and metabolic maps) and quantitatively (i.e., linewidth, SNR, metabolic ratios, Cramer-Rao lower bounds (CRLB)). For quantitative evaluation, a mask was drawn, which excluded ventricles and voxels that were partly outside the VOI and only voxels inside this mask were further processed. All in vivo spectra were quantified by LCModel software (Provencher, 2001), and metabolic ratios, as well as spectral quality parameters (i.e., SNR and linewidth of NAA) were calculated. The mean and the standard deviation of the metabolitic ratios, the SNR, linewidth, and CRLB were determined inside the mask to assess global changes in spectral quality and quantification.

To investigate also local changes, Bland-Altman plots were drawn for metabolic ratios, the SNR, linewidth, and CRLB using the static measurement without ShMoCo as the reference standard. The parameter means and the limits of agreement (1.96 times the standard deviation) were derived. Paired t-tests across all voxels and subjects were performed for all parameters to compare the reference standard (i.e., for standard resolution scans – static scan without ShMoCo; for high resolution scan – static scan with ShMoCo) with all remaining scans. A p<.05 was considered statistically significant.

3. Results

3.1. 3D-MRSI of phantoms

3.1.1. Localization correction

Our phantom localization tests showed that localization errors due to intra-scan movement (i.e., translations and rotations) can be accurately corrected in both the spiral-encoded direction and phase-encoded direction, respectively. Without ShMoCo, the same movement patterns lead to both localization errors and deteriorated spectral quality (Figures 2–5 Supplementary Material Figure 11).

3.1.2. Scanner frequency drift correction

The frequency drift that we observed during a 20-minute 3D-MRSI phantom scan was ~5–6 Hz (~15–18 Hz/hour). A similar frequency drift was observed during the long in vivo measurement in ~15 minutes (i.e., ~6 Hz or 24 Hz/hour), in addition to movement-related frequency changes (Figure 6).

3.2. 3D-MRSI of human subjects

3.2.1. Short low-resolution scan – moderate motion

For all three volunteers, the mask for quantitative comparison contained 442±36 voxels. In vivo metabolic maps showed no negative effects of ShMoCo on static measurements, but illustrated the efficient recovery of spatial 3D-MRSI localization that was corrupted without ShMoCo. The most obvious localization errors were found for right-left rotation, followed by translation, and up-down head rotation (Figure 7 and Supplementary Material Figure 12).

Figure 7.

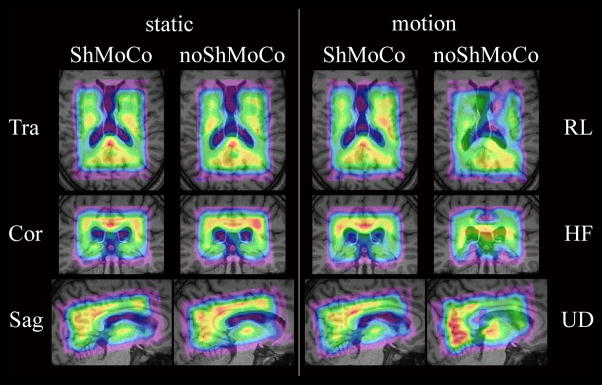
Figure 7

Open in a new tab

3D metabolic maps (i.e., NAA) obtained in a volunteer with standard-resolution 3D-MRSI in the presence of moderate motion. In total, metabolic maps of eight scans are displayed in three orthogonal planes. Odd columns display maps with ShMoCo, and even columns display maps without ShMoCo. The two columns on the left show all three orthogonal slices for each of the two static scans as a reference. The two columns on the right display the slice orientation that illustrates the largest localization errors that were caused for a specific head motion: (top) transversal for right-left (RL) rotation, (center) coronal for head-feet (HF) translation, and sagittal for up-down (UD) rotation. Without ShMoCo right-left translation caused the strongest observable localization errors, follow by head-feet translation, and up-down head rotation. One additional row beyond that defined by the VOI was quantified to show signal spill-over for noShMoCo.

When non-corrected motion vs. static scans were compared, motion led to a significantly reduced spectral quality (SNR −8% to −22%; linewidth +5% to +33%)(p<0.01) along with a less reliable spectral fitting (CRLB +23% to +348%)(p<0.01) that caused substantial corruption of local metabolic ratios. Although the average global metabolic ratios were similar, voxel-wise comparison (p<0.01) and Bland-Altman plots show a significant bias in local metabolic ratios, spectral quality, and quantification precision (Figure 8). The strongest average effects on quality parameters were observed for head-feet translation (Table 1)(p<0.001).

Figure 8.

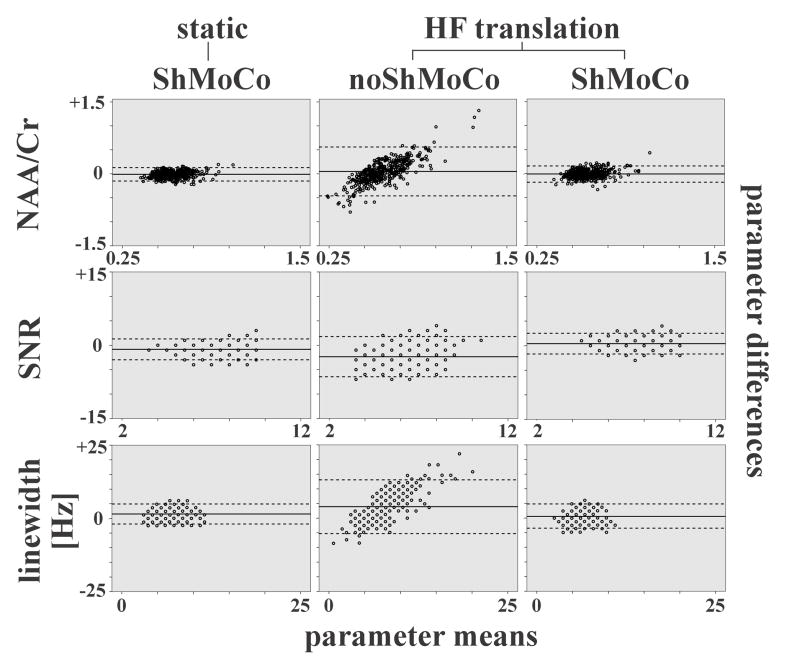
Figure 8

Open in a new tab

Bland-Altman plots are used to compare a reference scan (i.e., static reference scan without ShMoCo) with each of the following three test scans one-by-one: (left column) static with ShMoCo; (center column) head-feet translation without ShMoCo; (right column) head-feet translation with ShMoCo. The mean (x-axis) and difference (y-axis) of the reference scan and the each test scan are computed for all voxels inside the VOI and displayed in the diagrams for the following parameters: (top row) NAA/Cr; (center row) SNR; and (bottom row) linewidth.

The average parameter means (solid lines) between two corresponding scans and the limits of agreement (±1.96 times the standard deviation (dashed lines)) are displayed. Substantial local changes were observed as illustrates by significantly increased limits of agreement for scans without ShMoCo, while scans with ShMoCo presented similar limits of agreement as the reference scans.

Table 1.

Comparison of spectral quality (i.e., SNR, linewidth), quantification precision (i.e., CRLB), and metabolic ratios (i.e., Cr/NAA)(in mean ± standard deviation) obtained with/without ShMoCo-correction for two resolutions and different motion tasks.

task Corr SNR [] LW [Hz] CRLBNAA [%] CRLBCr [%] Cr/NAA []
Short low-resolution scan – moderate motion
static - 6.4±1.3 5.8±2.3 5.7±0.9 7.7±1.7 0.67±0.15
ShMoCo 6.2±1.4* 5.8±2.3 5.8±1.1 8.0±2.0 0.66±0.16
RL - 5.9±1.9* 6.1±2.6* 8.6±31.0* 9.7±8.8* 0.66±0.16*
ShMoCo 6.4±1.3 5.8±2.3 5.5±0.8 7.7±1.4 0.65±0.14
UD - 5.0±1.6* 7.7±3.0* 7.0±3.8* 12.0±47.8* 0.67±0.20*
ShMoCo 6.2±1.4 6.1±2.1 5.6±1.1 7.6±1.5 0.66±0.14
HF - 5.1±1.3* 6.8±2.2* 25.5±132.2* 15.5±68.0* 0.69±0.15*
ShMoCo 6.6±1.5 5.8±2.3 5.7±1.5 7.7±2.1 0.65±0.14
Long high-resolution scan – severe motion
static ShMoCo 5.5±1.1 5.3±1.7 6.8±1.8 9.4±2.7 0.64±0.15
HF+RL+UD - 3.9±1.8* 8.9±3.8* 27.8±122.8* 37.3±142.9* 0.66±0.25*
ShMoCo 4.9±1.0* 6.2±2.1* 7.0±1.6 10.1±4.3 0.63±0.14
Open in a new tab
*

- statistically significant difference (p<0.05)

ShMoCo – Real-time shim-, frequency, and motion correction; RL – right-left head rotation; UD – chin up-down rotation; HF –head-feet translation; SNR – signal-to-noise ratio; LW – linewidth; CRLB – Cramer-Rao lower bound; Cr – creatine; NAA – N-acetylaspartate

When corrected vs. non-corrected motion scans were compared, an improvement in spectral fitting (CRLB −20% to −78%), along with enhanced spectral quality (SNR +9% to +29%; linewidth −5% to −21%) was found for moderate motion (Table 1). The spectral quality (i.e., SNR (p=0.07–0.26), linewidth (p=0.11–0.34)), reliability of spectral fitting (p=0.09–0.94), and metabolic ratios (p=0.06–0.83) of the static 3D-MRSI scans and the corrected 3D-MRSI scans with moderate motion were comparable (Table 1). No difference in linewidth, CRLBs, and metabolic ratios was found between 3D-MRSI with ShMoCo and 3D-MRSI without ShMoCo in the static case, but we found a small difference in SNR (6.4±1.3 vs. 6.2±1.4; p=0.02) (Table 1).

3.2.2. Long high-resolution scan – severe motion

The mask for quantitative comparison of the high-resolution scans contained 456 voxels. If not corrected, the severe motion that was probed in the high-resolution scan resulted in an even stronger drop in spectral quality (SNR −29%; linewidth +68%)(p<0.001) and spectral fitting (CRLB +297% to 309%)(p<0.001) than for the standard-resolution scan, along with substantial lipid contamination that made quantification in some regions of the VOI impossible (Table 1)(Figure 9). Although, no anatomical features (i.e., position of ventricles) were observable on metabolic maps without ShMoCo (Figure 9) as spatial localization was clearly impaired and local metabolic Cr/NAA ratios were biased (Figure 8), differences in the average global metabolic Cr/NAA ratios were small (0.66±0.25 vs 0.64±0.15; p=0.01).

Figure 9.

Figure 9

Open in a new tab

Spectral grids are displayed for the high-resolution 3D-MRSI scan with severe motion in the transversal plane, along with a T1-weighted reference scan (top-left) illustrating the matrix and VOI position. Ventricle positions are outlines to serve as visual guides for the static case (top-right), the motion scan without ShMoCo (lower-left), and the motion scan with ShMoCo (lower-right). Two sample spectra that are displayed in the spectral grid for the static and the motion scan with ShMoCo are enlarged and shown as LCmodel software output, including original data points (black), fitted spectra (red), and residual (above). Although ShMoCo recovers most of the spectra throughout the brain compared to noShMoCo, the spectral quality near the frontal lobe was not fully recovered. In the spectral grid without motion correction large metabolite signal contamination of voxels located in the ventricles can be noticed. All spectra in grids are scaled to the same noise level.

Compared to the low-resolution scans the improvement observed for ShMoCo-corrected 3D-MRSI was stronger (SNR +26%; linewidth −30%; CRLB −73% to 75%)(p<0.001). The results were still slightly inferior to the static case (SNR −10%; linewidth +17%; CRLB +3% to 7%)(p<0.01) and the global metabolic ratios were similar (p=0.09) (Table 1). The visualization of local anatomical features on metabolic maps, such as the ventricles, was substantially improved (Figure 10).

Figure 10.

Figure 10

Open in a new tab

3D metabolic maps (i.e., NAA) obtained in the high-resolution 3D-MRSI session, with severe motion depicted in all three orthogonal planes for all three scans. Column #1 displays the positioning of the VOI/FOV using T1-weighted MEMPRAGE images for localization. Column #2 shows the reference metabolic maps obtained for the static case. Columns #3 and #4 depict the metabolic maps of scans with ShMoCo and without ShMoCo, respectively. ShMoCo recovers most of the anatomical features (i.e., ventricles), even if severe intra-scan motion is present during scans, whereas metabolic maps without ShMoCo are distorted by incorrect spatial localization, low spectral quality, and strong lipid contamination. One additional row/column beyond that defined by the VOI was quantified to show signal spill-over for noShMoCo.

4. Discussion

Our study demonstrates that robust and accurate high-resolution 3D-MRSI of the brain at 3T can be performed in the same scan time as SVS. The efficient combination of spiral 3D-LASER-MRSI with real-time motion-, shim-, and frequency-updating significantly improved the localization accuracy and spectral quality obtained in both phantoms and volunteers, even when there was strong motion or scanner drift during scans. This facilitates the use of 3D-MRSI in clinical routine where robustness is important to guarantee good results in a large range of patients and working conditions.

4.1. Motion and B0 correction

Several groups have found significantly improved MRS data quality, if motion correction was applied (Andrews-Shigaki et al., 2011; Boer et al., 2012; de Nijs et al., 2009; Ernst and Li, 2011; Helms and Piringer, 2001; Hess et al., 2012; Hess et al., 2011; Keating and Ernst, 2012; Kim et al., 2004; Lange et al., 2012; Lin et al., 2009; Posse et al., 1993; Thiel et al., 2002; Zaitsev et al., 2010). A common approach is the retrospective correction of frequency and phase, in particular for SVS (Ernst and Li, 2011; Helms and Piringer, 2001; Lin et al., 2009). However, this approach cannot correct for localization or shim errors.

For smaller voxels and imaging of heterogeneous tissues or lesions, maintaining accurate voxel localization during the whole scan is critical. If strong shim currents are necessary for good shimming results (i.e., in case of small VOIs or if the VOI includes areas that are difficult to shim near air cavities), position changes and scanner drift can lead to strong spatial B0 variations that cannot be well-corrected by frequency and phase correction alone (Andrews-Shigaki et al., 2011; Hess et al., 2012). Therefore, robust MRS necessitates comprehensive motion correction concepts that include updating of both position and shims.

4.2. Prospective motion and B0 correction approaches

Several groups have independently evaluated the benefits of prospective motion correction for MRS. Keating et al. proposed prospective motion correction for SVS using image-based spiral navigators for position correction and orthogonal 1D-field maps to determine optimal shims (Keating and Ernst, 2012). This approach was specifically designed for SVS.

Zaitsev et al. introduced prospective motion correction based on optical tracking for position corrections and interleaved reference scans for correction of temporal frequency drifts in SVS (Zaitsev et al., 2010), which was later extended for use with 2D-MRSI (Lange et al., 2012). This technique corrects for phase and frequency changes, but does not update shims. Lange et al. concluded that additional dynamic shim updating would be beneficial for correction of large through-plane motion (Lange et al., 2012). Similarly, Andrews et al. pointed out the need for dynamic shimming in prospectively corrected SVS (Andrews-Shigaki et al., 2011).

Hess et al. presented prospective motion correction using vNav for SVS (Hess et al., 2011) and 2D-MRSI (Hess et al., 2012), including position, shim, and frequency updates. They independently investigated the effects of real-time position- and shim-updating for 2D-MRSI, and concluded that dynamic shimming was the major factor that leads to significantly improved spectral quality. The amount of improvement was strongly dependent on the specific motion task. Nodding of the head led to the biggest change in B0 homogeneity (Hess et al., 2012). Although the whole 3D imaging navigator block was longer than in other prospectively corrected MRS studies, TR adjustments were similar to typically used timing parameters in MRS.

Our 3D-MRSI study supports the evidence of these other studies that found improved data quality in SVS (Andrews-Shigaki et al., 2011; Hess et al., 2011; Keating and Ernst, 2012; Zaitsev et al., 2010) and 2D-MRSI (Hess et al., 2012; Lange et al., 2012), if prospective motion correction was applied. With our ~700 ms long navigator block TRs as short as 1.6s can be easily achieved. Compared to previous SVS and 2D-MRSI studies, our 3D-MRSI results underline the importance of acquiring dynamic 3D field maps by dual-contrast EPI-based vNav. Other previous navigator approaches for MRS cannot cover the whole VOI of a 3D-MRSI volume that would be required for first-order shim correction along with real-time position and frequency correction. To our knowledge this is the first demonstration of motion corrected 3D-MRSI.

4.3. Volume of interest localization

Previous studies have reported significantly improved localization accuracy (i.e., better selection profiles, reduced chemical shift errors, and B1+-insensitivity) for MRSI using LASER and semi-LASER sequences at 3T (Andronesi et al., 2010; Scheenen et al., 2008). The LASER selection pulses (i.e., GOIA selection pulses with low-power requirements) used in this study provide a substantial reduction of maximum B1, SAR, chemical shift displacement errors, and pulse duration compared to normal adiabatic pulses (Andronesi et al., 2010). Additionally readjusting spoiler gradient setup shortened the minimum TE (i.e., 27 ms) of our LASER sequence below that of previous LASER sequences (Andronesi et al., 2010; Scheenen et al., 2008). Our minimum TE was 27ms compared to 50ms (Hess et al., 2012). The chemical shift displacement error was four times smaller and the SAR 40% lower than by (Hess et al., 2012). The TE in our study (i.e., 30 ms) is similar to short-echo PRESS sequences, but in contrast to PRESS, full LASER localization is insensitive to changes in B1+. Therefore, possible changes in B1+ due to motion cannot affect localization accuracy.

In our study, we have updated several gradient, RF, and postprocessing parameters. Similar to previous studies, VOI rotations were performed by adapting the gradient strength in all individual gradient axes. For gradient-modulated RF pulses, off-center shifting cannot be easily performed by adding an off-center-frequency (Andronesi et al., 2010). Real-time updating of our selective GOIA pulses required online recalculation of pulse modulation functions to readjust the current off-center-position. This was not necessary in previous studies that used only selective pulses with constant gradients (Hess et al., 2012).

4.4. Accelerated data acquisition

Acceleration of MRSI data acquisition by echo-planar or spiral encoding is a prerequisite for high-resolution 3D-MRSI. The ability to perform 3D metabolic mapping in the same measurement time as otherwise required for SVS is of immense clinical relevance (Adalsteinsson et al., 1998; Andronesi et al., 2012; Maudsley et al., 2009; Posse et al., 1995). In addition, spiral imaging is known to be less sensitive to motion due to gradient moment nulling effects (Delattre et al., 2010; Kim et al., 2004), and the possible reduction in scan time makes the occurrence of motion artifacts less likely (Adalsteinsson et al., 1998; Andronesi et al., 2012; Delattre et al., 2010; Kim et al., 2004). However, spiral-accelerated MRSI alone cannot completely avoid motion artifacts and the excessive stress on the gradient system associated with EPSI and spirals may lead to increased problems with temporal frequency drifts (Ebel and Maudsley, 2005; El-Sharkawy et al., 2006)(see 4.5).

Phase encoding as used in the motion correction paper by Hess et al. (Hess et al., 2012) is too slow for high-resolution 3D-MRSI. In our study, spiral encoding overcomes measurement time problems, but introduces increased frequency drift (see 4.5). This drift is not a problem in our study, because our vNav corrects for frequency drift without further effort to harness the benefits of spiral acceleration. We were, therefore able to acquire 3D-MRSI with 5.4 times higher spatial resolution than reported by Hess et al.

FOV off-center shifts in the phase-encoded direction were performed similarly to other MRSI studies (Hess et al., 2012; Lange et al., 2012). However, shifts in the spiral-encoded directions cannot be performed by adding a constant phase roll in the affected k-space axis. Real-time-monitored off-center information was used to correct x/y-plane shifts during online image reconstruction.

Our approach is different than a previously presented motion-compensated sequence for spiral trajectories, which relied on the characteristic of spiral MRSI sequences to repeatedly sample the kxy-space origin (Kim et al., 2004). Such a self-navigation approach is suitable for 2D-MRSI, but cannot be readily used for 3D-MRSI localization by a stack of spirals. In our study, phase encoding in the z-direction prevented repeated sampling of the k-space origin. Posse et al. introduced a different method that allows repeated sampling of the k-space origin, even for phase encoding (Posse et al., 1993). However, it may be difficult to combine this approach with self-navigation. In addition, both methods require a relatively high water signal to allow good estimation of phase properties from this single point in the k-space center, while position updates estimated by our vNav are automatically available and acquired before water is suppressed, so that good water suppression for MRSI can be maintained. Independent of these corrections, previous studies have found that spiral trajectories are less sensitive to motion due to gradient nulling effects, and are immune to many flow effects (Delattre et al., 2010; Kim et al., 2004), which makes a combination of spiral MRSI and prospective motion correction particularly desirable.

4.5. Scanner Instabilities

The frequency drift that we observed in our study (~15–24 Hz/hour) was significantly lower than that previously reported for EPSI (~40–50 Hz/hour)(Ebel and Maudsley, 2005) on the same type of scanner, but is still not negligible for longer 3D-MRSI measurements. On the other hand, Hess et al. did not observe such strong frequency drifts when using vNav for phase encoded MRSI or SVS (Hess et al., 2012; Hess et al., 2011). However, it should be noted that the heating that causes frequency drift depends on scanner installation and environmental factors (e.g., amount of shim iron, previous scans, magnet stability).

4.6. Limitations

Although several sources of motion artifacts were prospectively corrected and moderate motion artifacts were successfully eliminated, severe motion still led to an average 10% lower SNR and 17% higher linewidth than measured for static conditions. This loss in spectral quality is similar to that found in a previous study for 2D-MRSI (Hess et al., 2012) and is probably related to coil proximity changes, uncorrected higher-order (≥2nd) B0 changes, and a few spectra that are corrupted by motion during readout or the LASER localization. Our sequence is particularly suitable, if there are only a few movement events during the MRSI scan (e.g., coughing or occasional movement due to subject discomfort), followed and preceded by longer periods of no movement and if the movement within a single TR does not exceed a rotation of 8° or a translation of 2cm. Very fast motion (i.e. occurring within ~600ms between the navigator start and spiral readout) cannot be corrected. Also, continuously repeated subject movement during the whole measurement may be not corrected well.

Further improvements, such as reacquisition of seriously corrupted scans (Tisdall et al., 2012), updating of higher-order shim terms, and correction for coil sensitivity profile changes could lead to a full recovery of spectral quality.

Future sequence improvements, combinations of prospective motion correction methods, and advances in hardware technology will contribute further to the robust acquisition of 3D-MRSI in neuroscience and clinical routine. In particular, functional MRS studies could significantly benefit from real-time motion corrected MRS and MRSI acquisition (Schaller et al., 2013).

5. Conclusion

The combination of a spiral 3D-LASER-MRSI sequence with real-time ShMoCo provides accurate, fast, and robust 3D metabolic imaging of the human brain at 3T. This will further promote the use of MRS methods for neuroscience and routine clinical applications.

Supplementary Material

01. Figure 4 (supplementary data).

Localization experiment in cylindrical multi-compartment phantom simulating (a) rotation of the phantom by 45°, relative to the FOV (white square), in a counter-clockwise (spiral-encoded in-plane) orientation. In (b), the static case spectra of all three chemical compounds are localized well within their tubes, while in (c) rotation led to severe localization errors. These localization errors were eliminated by ShMoCo, and (d) localization accuracy and spectral quality were recovered. The white arrow illustrates the direction of movement.

02. Figure 5 (supplementary data).

Localization experiment in cylindrical multi-compartment phantom simulating (a) rotation of the phantom by 30°, relative to the FOV (white rectangle), in a coronal (phase/spiral-encoded through-plane) orientation. In (b), the static case spectra are localized well within the tube and VOI, while in (c), translation led to both a significant loss in spectral quality and severe localization errors. Both sources of error were eliminated by ShMoCo, and (d) localization accuracy and spectral quality were restored. The white arrow illustrates the direction of movement.

03. Figure 11 (supplementary data).

Motion graphs as measured by vNav for all phantom scans are plotted for (1st column) transversal translation; (2nd column) sagittal translation; (3rd column) transversal rotation; and (4th column) coronal rotation as a function of measurement time in the scanner coordinate system. Translation measures (top row) and rotation measures (bottom row) are displayed separately.

04. Figure 12 (supplementary data).

Bland-Altman plots are used to compare a reference scan (i.e., static reference scan without ShMoCo) with each of the following seven test scans one-by-one: (1st column) static with ShMoCo; (2nd column) right-left head rotation without ShMoCo; (3rd column) right-left head rotation with ShMoCo; (4th column) up-down head rotation without ShMoCo; (5th column) up-down head rotation with ShMoCo; (6th column) head-feet translation without ShMoCo; and (7th column) head-feet translation with ShMoCo. The mean (x-axis) and difference (y-axis) of the reference scan and the each test scan are computed for all voxels inside the VOI and displayed in the diagrams for the following parameters: (1st row) NAA/Cr; (2nd row) SNR; (3rd row) linewidth; and (4th row) Cramer-Rao lower bounds of NAA.

The average parameter means (solid lines) between two corresponding scans and the limits of agreement (±1.96 times the standard deviation (dashed lines)) are displayed. Substantial local changes were observed as illustrates by significantly increased limits of agreement for scans without ShMoCo, while scans with ShMoCo presented similar limits of agreement as the reference scans.

Figure 3.

Figure 3

Open in a new tab

Localization experiment in cylindrical multi-compartment phantom simulating (a) translation of the phantom by 8 cm, relative to the FOV (white rectangle), in the head-feet (phase-encoded through-plane) direction. In (b), the static case spectra are localized well within the tube and VOI, while in (c) translation led to both significant frequency position changes and severe localization errors. Both sources of error were eliminated by ShMoCo, and (d) localization accuracy and frequency position were corrected. The white arrow illustrates the direction of movement.

4. Highlights (for review).

  • Head motion and scanner instabilities degrade localization and spectral quality

  • Head position and B0 maps can be monitored in real-time by volumetric navigators

  • We corrected position errors by real-time updating of gradients and RF pulses

  • We restored spectral quality by real-time updating of B0 shims

  • We corrected scanner frequency drift by real-time frequency updating

Acknowledgments

This study was supported by the Austrian Science Fund (FWF): KLI-61 and J3302-B24 to W.B., and the KL2 MeRIT award to O.C.A. from the Harvard Clinical and Translational Science Center (8KL2TR000168-05) and 1K22CA178269-01 from NIH, National Cancer Institute.

Resources provided to Martinos Center by the Center for Functional Neuroimaging Technologies, P41EB015896, a P41 Regional Resource supported by the National Institute of Biomedical Imaging and Bioengineering (NIBIB), National Institutes of Health. This work also involved the use of instrumentation supported by the NIH Shared Instrumentation Grant Program and/or High-End Instrumentation Grant Program; specifically, grant S10RR021110. We gratefully thank Marjanska Malgorzata (Center for Magnetic Resonance Research at University of Minnesota) for providing the LCModel basis set and Himanshu Bhat (Siemens Healthcare, Charlestown, MA) for sequence programming support.

Footnotes

Parts of this study were presented at:

- Bogner, W. et al., Real-time motion and shim correction by volumetric EPI navigators improves 3D LASER localized spiral MRSI of the brain at 3T (talk #855). ISMRM, 2013. Salt Lake City

Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.

References

  1. Adalsteinsson E, Irarrazabal P, Topp S, Meyer C, Macovski A, Spielman DM. Volumetric spectroscopic imaging with spiral-based k-space trajectories. Magn Reson Med. 1998;39:889–898. doi: 10.1002/mrm.1910390606. [DOI] [PubMed] [Google Scholar]
  2. Andrews-Shigaki BC, Armstrong BS, Zaitsev M, Ernst T. Prospective motion correction for magnetic resonance spectroscopy using single camera Retro-Grate reflector optical tracking. J Magn Reson Imaging. 2011;33:498–504. doi: 10.1002/jmri.22467. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Andronesi OC, Gagoski BA, Sorensen AG. Neurologic 3D MR Spectroscopic Imaging with Low-Power Adiabatic Pulses and Fast Spiral Acquisition. Radiology. 2012;262:647–661. doi: 10.1148/radiol.11110277. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Andronesi OC, Ramadan S, Ratai EM, Jennings D, Mountford CE, Sorensen AG. Spectroscopic imaging with improved gradient modulated constant adiabaticity pulses on high-field clinical scanners. Journal of Magnetic Resonance. 2010;203:283–293. doi: 10.1016/j.jmr.2010.01.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Benner T, Wisco JJ, van der Kouwe AJ, Fischl B, Vangel MG, Hochberg FH, Sorensen AG. Comparison of manual and automatic section positioning of brain MR images. Radiology. 2006;239:246–254. doi: 10.1148/radiol.2391050221. [DOI] [PubMed] [Google Scholar]
  6. Boer VO, van de Bank BL, van Vliet G, Luijten PR, Klomp DW. Direct B0 field monitoring and real-time B0 field updating in the human breast at 7 Tesla. Magn Reson Med. 2012;67:586–591. doi: 10.1002/mrm.23272. [DOI] [PubMed] [Google Scholar]
  7. Bogner W, Gruber S, Trattnig S, Chmelik M. High-resolution mapping of human brain metabolites by free induction decay (1)H MRSI at 7 T. NMR Biomed. 2012;25:873–882. doi: 10.1002/nbm.1805. [DOI] [PubMed] [Google Scholar]
  8. de Nijs R, Miranda MJ, Hansen LK, Hanson LG. Motion correction of single-voxel spectroscopy by independent component analysis applied to spectra from nonanesthetized pediatric subjects. Magn Reson Med. 2009;62:1147–1154. doi: 10.1002/mrm.22129. [DOI] [PubMed] [Google Scholar]
  9. Delattre BM, Heidemann RM, Crowe LA, Vallee JP, Hyacinthe JN. Spiral demystified. Magn Reson Imaging. 2010;28:862–881. doi: 10.1016/j.mri.2010.03.036. [DOI] [PubMed] [Google Scholar]
  10. Duarte JM, Lei H, Mlynarik V, Gruetter R. The neurochemical profile quantified by in vivo 1H NMR spectroscopy. Neuroimage. 2012;61:342–362. doi: 10.1016/j.neuroimage.2011.12.038. [DOI] [PubMed] [Google Scholar]
  11. Ebel A, Maudsley AA. Detection and correction of frequency instabilities for volumetric 1H echo-planar spectroscopic imaging. Magn Reson Med. 2005;53:465–469. doi: 10.1002/mrm.20367. [DOI] [PubMed] [Google Scholar]
  12. El-Sharkawy AM, Schar M, Bottomley PA, Atalar E. Monitoring and correcting spatio-temporal variations of the MR scanner’s static magnetic field. MAGMA. 2006;19:223–236. doi: 10.1007/s10334-006-0050-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Ernst T, Li J. A novel phase and frequency navigator for proton magnetic resonance spectroscopy using water-suppression cycling. Magn Reson Med. 2011;65:13–17. doi: 10.1002/mrm.22582. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Fu ZW, Wang Y, Grimm RC, Rossman PJ, Felmlee JP, Riederer SJ, Ehman RL. Orbital navigator echoes for motion measurements in magnetic resonance imaging. Magn Reson Med. 1995;34:746–753. doi: 10.1002/mrm.1910340514. [DOI] [PubMed] [Google Scholar]
  15. Garwood M, DelaBarre L. The return of the frequency sweep: designing adiabatic pulses for contemporary NMR. J Magn Reson. 2001;153:155–177. doi: 10.1006/jmre.2001.2340. [DOI] [PubMed] [Google Scholar]
  16. Helms G, Piringer A. Restoration of motion-related signal loss and line-shape deterioration of proton MR spectra using the residual water as intrinsic reference. Magn Reson Med. 2001;46:395–400. doi: 10.1002/mrm.1203. [DOI] [PubMed] [Google Scholar]
  17. Hess AT, Andronesi OC, Tisdall MD, Sorensen AG, van der Kouwe AJW, Meintjes EM. Real-time motion and B-0 correction for localized adiabatic selective refocusing (LASER) MRSI using echo planar imaging volumetric navigators. Nmr in Biomedicine. 2012;25:347–358. doi: 10.1002/nbm.1756. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Hess AT, Tisdall MD, Andronesi OC, Meintjes EM, van der Kouwe AJW. Real-Time Motion and B-0 Corrected Single Voxel Spectroscopy Using Volumetric Navigators. Magnetic Resonance in Medicine. 2011;66:314–323. doi: 10.1002/mrm.22805. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Jenkinson M. Fast, automated, N-dimensional phase-unwrapping algorithm. Magn Reson Med. 2003;49:193–197. doi: 10.1002/mrm.10354. [DOI] [PubMed] [Google Scholar]
  20. Keating B, Ernst T. Real-time dynamic frequency and shim correction for single-voxel magnetic resonance spectroscopy. Magn Reson Med. 2012;68:1339–1345. doi: 10.1002/mrm.24129. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Kim DH, Adalsteinsson E, Spielman DM. Spiral readout gradients for the reduction of motion artifacts in chemical shift imaging. Magn Reson Med. 2004;51:458–463. doi: 10.1002/mrm.20004. [DOI] [PubMed] [Google Scholar]
  22. Kreis R. Issues of spectral quality in clinical H-1-magnetic resonance spectroscopy and a gallery of artifacts. Nmr in Biomedicine. 2004;17:361–381. doi: 10.1002/nbm.891. [DOI] [PubMed] [Google Scholar]
  23. Lange T, Maclaren J, Buechert M, Zaitsev M. Spectroscopic imaging with prospective motion correction and retrospective phase correction. Magn Reson Med. 2012;67:1506–1514. doi: 10.1002/mrm.23136. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Lin JM, Tsai SY, Liu HS, Chung HW, Mulkern RV, Cheng CM, Yeh TC, Chen NK. Quantification of non-water-suppressed MR spectra with correction for motion-induced signal reduction. Magn Reson Med. 2009;62:1394–1403. doi: 10.1002/mrm.22119. [DOI] [PubMed] [Google Scholar]
  25. Maclaren J, Herbst M, Speck O, Zaitsev M. Prospective motion correction in brain imaging: A review. Magn Reson Med. 2012 doi: 10.1002/mrm.24314. [DOI] [PubMed] [Google Scholar]
  26. Maudsley AA, Domenig C, Govind V, Darkazanli A, Studholme C, Arheart K, Bloomer C. Mapping of brain metabolite distributions by volumetric proton MR spectroscopic imaging (MRSI) Magn Reson Med. 2009;61:548–559. doi: 10.1002/mrm.21875. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Ooi MB, Krueger S, Thomas WJ, Swaminathan SV, Brown TR. Prospective real-time correction for arbitrary head motion using active markers. Magn Reson Med. 2009;62:943–954. doi: 10.1002/mrm.22082. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Posse S, Cuenod CA, Le Bihan D. Motion artifact compensation in 1H spectroscopic imaging by signal tracking. Journal of Magnetic Resonance Series B. 1993;102:222–227. [Google Scholar]
  29. Posse S, Tedeschi G, Risinger R, Ogg R, Le Bihan D. High speed 1H spectroscopic imaging in human brain by echo planar spatial-spectral encoding. Magn Reson Med. 1995;33:34–40. doi: 10.1002/mrm.1910330106. [DOI] [PubMed] [Google Scholar]
  30. Provencher SW. Automatic quantitation of localized in vivo 1H spectra with LCModel. NMR Biomed. 2001;14:260–264. doi: 10.1002/nbm.698. [DOI] [PubMed] [Google Scholar]
  31. Schaller B, Mekle R, Xin L, Kunz N, Gruetter R. Net increase of lactate and glutamate concentration in activated human visual cortex detected with magnetic resonance spectroscopy at 7 tesla. J Neurosci Res. 2013 doi: 10.1002/jnr.23194. [DOI] [PubMed] [Google Scholar]
  32. Scheenen TWJ, Klomp DWJ, Wijnen JP, Heerschap A. Short echo time H-1-MRSI of the human brain at 3T with minimal chemical shift displacement errors using adiabatic refocusing pulses. Magnetic Resonance in Medicine. 2008;59:1–6. doi: 10.1002/mrm.21302. [DOI] [PubMed] [Google Scholar]
  33. Tannus A, Garwood M. Adiabatic pulses. NMR Biomed. 1997;10:423–434. doi: 10.1002/(sici)1099-1492(199712)10:8<423::aid-nbm488>3.0.co;2-x. [DOI] [PubMed] [Google Scholar]
  34. Thesen S, Heid O, Mueller E, Schad LR. Prospective acquisition correction for head motion with image-based tracking for real-time fMRI. Magn Reson Med. 2000;44:457–465. doi: 10.1002/1522-2594(200009)44:3<457::aid-mrm17>3.0.co;2-r. [DOI] [PubMed] [Google Scholar]
  35. Thiel T, Czisch M, Elbel GK, Hennig J. Phase coherent averaging in magnetic resonance spectroscopy using interleaved navigator scans: compensation of motion artifacts and magnetic field instabilities. Magn Reson Med. 2002;47:1077–1082. doi: 10.1002/mrm.10174. [DOI] [PubMed] [Google Scholar]
  36. Tisdall MD, Hess AT, Reuter M, Meintjes EM, Fischl B, van der Kouwe AJW. Volumetric navigators for prospective motion correction and selective reacquisition in neuroanatomical MRI. Magnetic Resonance in Medicine. 2012;68:389–399. doi: 10.1002/mrm.23228. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Tkac I, Oz G, Adriany G, Ugurbil K, Gruetter R. In vivo 1H NMR spectroscopy of the human brain at high magnetic fields: metabolite quantification at 4T vs. 7T. Magn Reson Med. 2009;62:868–879. doi: 10.1002/mrm.22086. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. van der Kouwe AJ, Benner T, Salat DH, Fischl B. Brain morphometry with multiecho MPRAGE. Neuroimage. 2008;40:559–569. doi: 10.1016/j.neuroimage.2007.12.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. van der Kouwe AJW, Benner T, Dale AM. Real-time rigid body motion correction and shimming using cloverleaf navigators. Magnetic Resonance in Medicine. 2006;56:1019–1032. doi: 10.1002/mrm.21038. [DOI] [PubMed] [Google Scholar]
  40. van der Kouwe AJW, Benner T, Fischl B, Schmitt F, Salat DH, Harder M, Sorensen AG, Dale A. On-line automatic slice positioning for brain MR imaging. Neuroimage. 2005;27:222–230. doi: 10.1016/j.neuroimage.2005.03.035. [DOI] [PubMed] [Google Scholar]
  41. Welch EB, Manduca A, Grimm RC, Ward HA, Jack CR., Jr Spherical navigator echoes for full 3D rigid body motion measurement in MRI. Magn Reson Med. 2002;47:32–41. doi: 10.1002/mrm.10012. [DOI] [PubMed] [Google Scholar]
  42. White N, Roddey C, Shankaranarayanan A, Han E, Rettmann D, Santos J, Kuperman J, Dale A. PROMO: Real-time prospective motion correction in MRI using image-based tracking. Magn Reson Med. 2010;63:91–105. doi: 10.1002/mrm.22176. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Zaitsev M, Speck O, Hennig J, Buchert M. Single-voxel MRS with prospective motion correction and retrospective frequency correction. NMR Biomed. 2010;23:325–332. doi: 10.1002/nbm.1469. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

01. Figure 4 (supplementary data).

Localization experiment in cylindrical multi-compartment phantom simulating (a) rotation of the phantom by 45°, relative to the FOV (white square), in a counter-clockwise (spiral-encoded in-plane) orientation. In (b), the static case spectra of all three chemical compounds are localized well within their tubes, while in (c) rotation led to severe localization errors. These localization errors were eliminated by ShMoCo, and (d) localization accuracy and spectral quality were recovered. The white arrow illustrates the direction of movement.

NIHMS537933-supplement-01.tif (807.1KB, tif)
02. Figure 5 (supplementary data).

Localization experiment in cylindrical multi-compartment phantom simulating (a) rotation of the phantom by 30°, relative to the FOV (white rectangle), in a coronal (phase/spiral-encoded through-plane) orientation. In (b), the static case spectra are localized well within the tube and VOI, while in (c), translation led to both a significant loss in spectral quality and severe localization errors. Both sources of error were eliminated by ShMoCo, and (d) localization accuracy and spectral quality were restored. The white arrow illustrates the direction of movement.

NIHMS537933-supplement-02.tif (702.3KB, tif)
03. Figure 11 (supplementary data).

Motion graphs as measured by vNav for all phantom scans are plotted for (1st column) transversal translation; (2nd column) sagittal translation; (3rd column) transversal rotation; and (4th column) coronal rotation as a function of measurement time in the scanner coordinate system. Translation measures (top row) and rotation measures (bottom row) are displayed separately.

NIHMS537933-supplement-03.tif (745.7KB, tif)
04. Figure 12 (supplementary data).

Bland-Altman plots are used to compare a reference scan (i.e., static reference scan without ShMoCo) with each of the following seven test scans one-by-one: (1st column) static with ShMoCo; (2nd column) right-left head rotation without ShMoCo; (3rd column) right-left head rotation with ShMoCo; (4th column) up-down head rotation without ShMoCo; (5th column) up-down head rotation with ShMoCo; (6th column) head-feet translation without ShMoCo; and (7th column) head-feet translation with ShMoCo. The mean (x-axis) and difference (y-axis) of the reference scan and the each test scan are computed for all voxels inside the VOI and displayed in the diagrams for the following parameters: (1st row) NAA/Cr; (2nd row) SNR; (3rd row) linewidth; and (4th row) Cramer-Rao lower bounds of NAA.

The average parameter means (solid lines) between two corresponding scans and the limits of agreement (±1.96 times the standard deviation (dashed lines)) are displayed. Substantial local changes were observed as illustrates by significantly increased limits of agreement for scans without ShMoCo, while scans with ShMoCo presented similar limits of agreement as the reference scans.

NIHMS537933-supplement-04.tif (834.4KB, tif)

RESOURCES