Location via proxy:   [ UP ]  
[Report a bug]   [Manage cookies]                
Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2021 Feb 24.
Published in final edited form as: Proc IEEE Int Symp Biomed Imaging. 2018 May 24;2018:679–682. doi: 10.1109/isbi.2018.8363665

DENOISING AND DEINTERLEAVING OF EPSI DATA USING STRUCTURED LOW-RANK MATRIX RECOVERY

Ipshita Bhattacharya 1, Mathews Jacob 1
PMCID: PMC7902243  NIHMSID: NIHMS1667934  PMID: 33633819

Abstract

Echo-planar spectroscopic imaging (EPSI) sequence with spectrally interleaving is often used to rapidly collect metabolic MRI data. The main problem in using it on high field scanners is the presence of spurious peaks resulting from phase distortions between interleaves as well as the low signal to noise ratio. We introduce a novel structured low-rank framework for the simultaneous denoising and deinterleaving of spectrally interleaved EPSI data. The proposed algorithm exploits annihilation relations resulting from the linear predicability of exponential signals as well as due to uncorrected phase relations between interleaves. The algorithm is formulated as a structured nuclear norm minimization of a block Hankel matrix, derived from the interleaves. Experiments using hyperpolarized 13C mouse kidney EPSI data demonstrate the ability of the algorithm to remove ghost peaks from EPSI data collected using bipolar readout gradients.

Keywords: echo planar spectroscopic imaging, odd and even echoes, ghost peaks, structured low-rank recovery

1. INTRODUCTION

Shortening scan time has been a prime focus of magnetic spectroscopic imaging (MRSI) research [1, 2]. EPSI [?, ?] achieves accelerated data acquisition by using echo-planar readouts to simultaneously encode one spectral and one spatial dimension in one acquisition. This approach offers a speed up that is equal to number of points along one spatial dimension. However, it imposes high demands on the gradient system to maintain sufficient spectral resolution on high field systems that have greater spectral dispersion. A common practice to achieving sufficient spectral resolution is spectral interleaving, where the readouts are delayed in time for each spectral interleave. The data from multiple interleaves are upsampled and interlaced to form the final spectrum. A challenge associated with this strategy is the phase inconsistencies between interleaves, resulting from timing errors in the applied gradient trains, drifts in the magnetic field, and dependence on field inhomogeneity distortions. This problem is similar to Nyquist ghosting artifacts in echo-planar imaging (EPI), which manifests as Nyquist ghosts in the phase encoding dimension. In EPSI acquisitions, the phase inconsistencies manifest as spurious peaks in the spectra, which often makes the interpretation of the data challenging. Specifically, the proximity of a spurious peak from a strong metabolite may result in lineshape changes, affecting the accurate quantification of a relatively weak metabolite. Likewise, the intensity of the true peak may also be reduced since the energy is split between the true peak and ghost peak.

Several methods have been developed for the reduction of spectral ghosts in EPSI data. The conventional approach processes the odd and even echoes separately [6] reducing the spectral bandwidth by half; hence is not an option for high field scanners. Methods relying on theoretical estimates of k-t space trajectory such as the interlaced Fourier transform method [7] or the Fourier shift method [8] ignore the phase distortion between the echos. Echo misalignment [6, 7] correction has shown good potential in the reduction of spurious peaks, contingent to accurate estimation of k-t space trajectory that is often not practical in the presence of drifts and B0 inhomogeneity. Another popular method is to estimate the phase inconsistencies from the center of k-space and correct for the misalignment between the echoes [5] during data processing. Even though this method has shown promise in fat-water imaging, its utility for low-intensity metabolites is yet to be seen.

We introduce a novel reconstruction method for EPSI data which does not depend on accurate estimates of phase inconsistencies or k-t space trajectory to suppress the spectral ghosts. We exploit the annihilation relations in spectrally interleaved EPSI data resulting from the linear predictability of exponential signals and phase relations between the interleaves. We pose the problem as a recovery of two signals at each pixel, corresponding to the odd and even interleaves. The proposed framework is inspired by our MUSSELS strategy used in multishot EPI acquisitions [9], which is conceptually similiar to [10, 11]. Unlike these methods [9, 10, 11] that rely on coil sensitivity information or signal smoothness to avoid the trivial solution resulting from uniform undersampling, we rely on the annihilation property due to linear predictability of the exponentials. We construct a block Hankel matrix, whose entries correspond to the two echoes, that capture the annihilation relations in a compact way; the annihilation relations translate to a low-rank block Hankel matrix, which we recover from undersampled measurements using structured nuclear norm minimization. / We demonstrate the results of the proposed method using high resolution 13C MRSI data of mouse kidney acquired at 9.4T using bipolar EPSI readout gradients. The proposed methods show improvement in the signal of Pyruvate maps due to recovery of real spectral peaks and reduction of spurious peaks leading from combination of odd and even echoes.

2. BACKGROUND

We assume that the true spectrum at a specified pixel r as a multi-exponential model:

ρ[r,n]=∑k=1Kck[r](νk)n;n=0,..,N−1 (1)

where K is the number of exponentials with parameters

νk=exp{−(1T2,k*+j2πfk)T}, (2)

and ck are amplitudes. Here (1T2,k*+j2πfk) are the exponential parameters of the kth exponential and T is the Nyquist sampling interval. We will omit the dependence of the signal on the spatial location for simplicity in the future discussions. The Fourier transform of the signal along n, specified by

ρ^[k]=∑n=1Nρ[n]exp(−j2πNkn) (3)

will have K peaks at frequencies fk; the basic goal in MR spectroscopy is to estimate the amplitudes ck from the data.

Since the bandwidth of the spectrum is too large in high field scanners, it is often impossible to sample the signal at the Nyquist rate using EPSI. It is a common practice to acquire the data using spectral interleaving, where the signal is sampled twice with a sampling interval of 2T. Specifically, one would acquire two signals ρo[n] and ρe[n], where the readout of the odd signal is delayed by T, These signals are later combined as

ρcombined[n]={ρe[n]ifnisevenρo[n]ifnisodd (4)

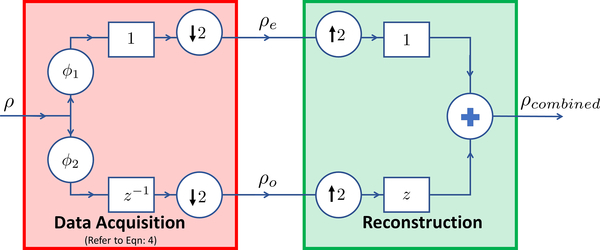
Unfortunately, ρe and ρo are acquired at two different acquisitions and hence would differ in terms of a phase distortion. The distortion is often a complex function of the readout delay T and the field inhomogeneity at the spatial location r. Hence, the combined signal (4) often suffers from spectral ghosts, shifted from the original point by N/2 spectral points; the distribution of the amplitudes to the two peaks is dependent on the phase distortion. A schematic diagram explaining the signal formation is shown in Fig.1.

Fig. 1:

Fig. 1:

Open in a new tab

The FID at each pixel rho are corrupted by different phase distortion functions ϕ1 & ϕ2 before combining the odd (ρo) and even (ρe) as shown in the data acquisition block as described in Eqn:4. Standard schemes form the interleaved signal ρcombined as shown in the reconstruction block. We propose to replace the reconstruction by Eqn: 13.

3. METHODS

We introduce an algorithm for the removal of spurious peaks as well as the denoising of spectroscopic MRI data. The algorithm exploits the annihilation relations induced by the spectral model (1) as well as the phase relations in (5) & (6). We use a lifting strategy, where a structured matrix is formed using the entries of the measured signals ρe and ρo to exploit the annihilation relations. The rank of the structured matrix is very low due to the annihilation relations. We use the low-rank property to jointly recover the fully sampled signals ρe[n]; n = 0,..,N − 1 and ρo[n]; n = 0,..,N − 1 from their undersampled measurements.

We model the phase distortions in ρe and ρo as convolutions by finite impulse response filters ge[n] and go[n], respectively. Specifically, we assume that

ρ^e[k]=ρ^[k]g^e[k] (5)
ρ^o[k]=ρ^[k]g^o[k], (6)

where the signals ge[k] and go[k] are specified by

g[k]=∑p=−MMc[k]exp(−j2πpkN) (7)

Note that the above model can easily account for differences in phases and differences in frequencies in a small range determined by T, between the two acquisitions.

3.1. Annihilation relations induced by exponential model

Exponential signals in (1) satisfy an annihilation relation [12, 13]:

ρ[n]∗h[n]=0, (8)

where h is the FIR filter of the form

h(z)=∏i=1K(1−νkz−1). (9)

Since ρe(z) = ρ(z)he(z) and ρo = ρ(z)ho(z), both of these signals also satisfy (8) with the same filter. The convolution relation in (8) can be expressed as in the matrix form as Qeh = 0 and Qoh = 0, where Qe and Qo are (N − K + 1) × K dimensional Hankel matrices formed from the samples of ρo and ρe, respectively. In reality, the number of exponentials K is unknown, when one can overestimate it as P. In this case, any filter specified by hn(z) = h(z)η(z) such that hn is a P tap filter also annihilates the signal. Since one can find P − K linearly independent filters η(z), the rank of the (N − P + 1) × P dimensional matrices Qo and Qe can be shown to be equal to K − 1 (see [12] for details).

3.2. Annihilation property induced by phase relations

The model specified by (6) and (5) implies that there exists annihilation relations between the two signals

ρe[n]∗go[n]−ρe[n]∗ge[n]=0. (10)

This annihilation relation can be represented in the matrix form as

[Qe,Qo]︸Q[go−ge]=0, (11)

where Qo=T(ρo) and Qe=T(ρe) are (N − M + 1) × M dimensional convolution (Hankel) matrices obtained from the samples ρo[n] and ρe[n], respectively.

In reality, one often does not know the precise value of M needed to model the phase distortion; we overestimate the support to P ≥ M. In this case, there are multiple annihilation relations, involving filters g˜o(z)=go(z)γ(z) and g˜e(z)=ge(z)γ(z), where γ(z) is an arbitrary filter such that h˜o(z) and h˜e(z) are still support limited within M. This implies that the matrix H is low-rank.

We note that the combined lifting will benefit from both the exponential structure and phase relations. Specifically, we have

[Qe,Qo]︸Q[go∗γh∗η0−ge∗γ0h∗η]=0, (12)

Both the annihilation relations together result in a matrix with small rank.

3.3. Proposed structured low-rank algorithm

We use the low-rank structure of Q to recover the two signals μo and μe from their undersampled measurements:

{μo,μe}=argminμo,μe‖Aoμo−ρo‖2+‖Aeμe−ρe‖2+λ‖[T(μo),T(μe)]︸Q‖*, (13)

where Ao and Ae are undersampling operators corresponding to ρo and ρe, respectively. We use an iteratively reweighted nuclear norm minimization algorithm to minimize the above cost function and recover the signals. Post recovery, we will use root mean square of μo & μe as the recovered spectrum. Since exponential signals with fewer exponential parameters are associated with lower rank, the proposed formulation performs simultaneous denoising and deinterleaving.

The periodic undersampling pattern that results from interleaved sampling may result in a trivial solution, if the spectral annihilation relations are not exploited [11]. Specifically, the trivial solution μo = ρcombined = μe will satisfy the data consistency relations and the trivial annihilation relation μe[n]∗δ[n]−μe[n]∗δ[n]=0, resulting in a matrix of rank P. However, when the signal follow a multiexponential model as in (1), we observe that the trivial solution has 2K (double the number of exponential parameters), when compared to the true solution due to aliasing. This shows that the trivial solution is not the one that satisfies the data consistency constraints and yield the minimum rank of Q.

4. EXPERIMENTS AND RESULTS

A 9.4T small animal imaging scanner (Bruker BioSpin MRI GmbH, Germany) equipped with 1H−13C dual-tuned mouse volume Tx/Rx coil was used for all experiments [15]. [1-13C] pyruvic acid doped with 15mM Trityl radical and 1.5M Dotarem was polarized for 1 hour using HyperSense DNP polarizer (Oxford Instruments, Oxford, UK). Hyperpolarized sample was dissolved with Tris/EDTA-NaOH solution, and 350ul of pyruvate was injected into Balb/c mouse through tail vein catheter over duration of 5s. Axial oriented slice containing mouse kidney of 3 mm thickness was selected, and the scan was started at 5s after injection of the pyruvate. All procedures of the animal experiments were approved by the local animal care and use committee. EPSI data of matrix size 64 × 64 was collected using a bipolar gradient with 64 spectral points. Combination of odd and even echoes achieved a spectral bandwidth of 1562.5 Hz.

We compared the algorithm with phase correction method [5]. In Fig.2(a) the reference 1H image with three reference pixels are shown. Fig.2(b–d) & (f–g) show the spurious peak frame and pyruvate maps for all methods. The spurious peak frame shows reduced intensity for the proposed method which corresponds to improved removal of spurious peaks. The proposed method shows improved signal concentration for the pyruvate maps in areas as shown by the arrows. The percentage difference map in Fig.2(e) shows upto 70% increased signal recovered by the proposed method compared to the uncorrected data.

Fig. 2:

Fig. 2:

Open in a new tab

Metabolite maps: (a) 1H reference image of mouse kidney with reference pixels marked in three regions. (b-d) Intensity map at the spurious peak corresponding to Pyruvate and (f-h) Pyruvate maps, for the uncorrected data, phase correction method and proposed method respectively. (e) Map showing percentage increase of signal intensity provided by proposed method compared to uncorrected data. Pixels show upto 70% increase.

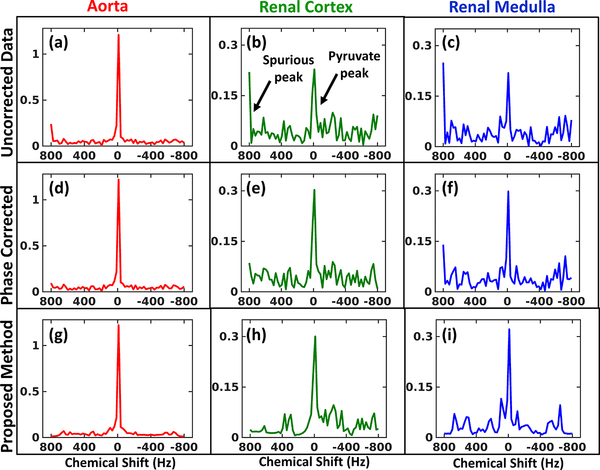
The spectra in Fig.3 from three regions of the kidney (aorta, cortex & medulla) show complete removal of spurious peaks and also exhibits denoising. The phase correction provides no denoising and also has sub-optimal performance especially for the renal medulla (blue) pixel.

Fig. 3:

Fig. 3:

Open in a new tab

Metabolite spectra: First (a-c), second (d-f) and third (g-i) row show the spectra at aorta, renal cortex and renal medulla respectively (refernce pixel location marked in Fig.2(a)) for the uncorrected data, phase correction method and the proposed method respectively.

5. CONCLUSION

In this work we proposed a novel algorithm for denoising and deinterleaving of EPSI data without directly estimating phase or relying on theoretical k-space trajectory. We further demonstrated the improvement offered by the proposed method compared to the classical phase correction method. The proposed scheme would be highly beneficial in reconstruction and correction of high-resolution EPSI, especially for the acquisition from high field magnets.

Acknowledgments

This work is supported by grants NSF CCF-1116067 and ONR-N000141310202. The data used in the study was provided by Hansol Lee and Dong-Hyun Kim of Yonsei University College of Medicine, Seoul, Republic of Korea.

6. REFERENCES

  • [1].Bhattacharya Ipshita and Jacob Mathews, “Compartmentalized low-rank recovery for high-resolution lipid unsuppressed mrsi,” MRM, vol. 78, no. 4, pp. 1267–1280, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • [2].Bhattacharya Ipshita and Jacob Mathews, “Compartmentalized low-rank regularization with orthogonality constraints for high-resolution mrsi,” in ISBI. IEEE, 2016, pp. 960–963. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • [3].Eslami Ramin and Jacob Mathews, “Robust reconstruction of mrsi data using a sparse spectral model and high resolution mri priors,” IEEE transactions on medical imaging, vol. 29, no. 6, pp. 1297–1309, 2010. [DOI] [PubMed] [Google Scholar]
  • [4].Bhave Sampada, Eslami Ramin, and Jacob Mathews, “Sparse spectral deconvolution algorithm for noncartesian mr spectroscopic imaging,” Magnetic resonance in medicine, vol. 71, no. 2, pp. 469–476, 2014. [DOI] [PubMed] [Google Scholar]
  • [5].Sarkar Shantanu, Heberlein Keith, Metzger Gregory J, Zhang Xiaodong, and Hu Xiaoping, “Applications of high-resolution echoplanar spectroscopic imaging for structural imaging,” JMRI, vol. 10, no. 1, pp. 1–7, 1999. [DOI] [PubMed] [Google Scholar]
  • [6].Metzger Gregory and Hu Xiaoping, “Application of interlaced fourier transform to echo-planar spectroscopic imaging,” JMR, vol. 125, no. 1, pp. 166–170, 1997. [DOI] [PubMed] [Google Scholar]
  • [7].Hanson Lars G, Schaumburg Kjeld, and Paulson Olaf B, “Reconstruction strategy for echo planar spectroscopy and its application to partially undersampled imaging,” MRM, vol. 44, no. 3, pp. 412–417, 2000. [DOI] [PubMed] [Google Scholar]
  • [8].Du Weiliang, Du Yiping P, Fan Xiaobing, Zamora Marta A, and Karczmar Gregory S, “Reduction of spectral ghost artifacts in high-resolution echo-planar spectroscopic imaging of water and fat resonances,” MRM, vol. 49, no. 6, pp. 1113–1120, 2003. [DOI] [PubMed] [Google Scholar]
  • [9].Mani Merry, Jacob Mathews, Kelley Douglas, and Magnotta Vincent, “Multi-shot sensitivity-encoded diffusion data recovery using structured low-rank matrix completion (mussels),” MRM, vol. 78, no. 2, pp. 494–507, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • [10].Lee Juyoung, Jin Kyong Hwan, and Ye Jong Chul, “Reference-free single-pass epi nyquist ghost correction using annihilating filter-based low rank hankel matrix (aloha),” MRM, vol. 76, no. 6, pp. 1775–1789, 2016. [DOI] [PubMed] [Google Scholar]
  • [11].Lobos Rodrigo A, Kim Tae Hyung, Hoge W Scott, and Haldar Justin P, “Navigator-free epi ghost correction using low-rank matrix modeling: Theoretical insights and practical improvements,” in Proc. ISMRM, 2017, p. 0449. [Google Scholar]
  • [12].Balachandrasekaran Arvind, Magnotta Vincent, and Jacob Mathews, “Recovery of damped exponentials using structured low rank matrix completion,” arXiv preprint arXiv:1704.04511, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • [13].Stoica Petre and Moses Randolph L, Introduction to spectral analysis, vol. 1, Prentice hall Upper Saddle River, New Jersey, USA, 1997. [Google Scholar]
  • [14].Lee Hansol, Song Jae E, Shin Jaewook, Joe Eunhae, Choi Young-suk, Song Ho-Taek, and Kim Dong-Hyun, “High resolution hyperpolarized 13c mrsi acquired by applying spice in mouse kidney,” in Proc. ISMRM, 2017, p. 3698. [Google Scholar]

RESOURCES