Abstract
The Drug Design Data Resource (D3R) ran Grand Challenge 2 (GC2) from September 2016 through February 2017. This challenge was based on a dataset of structures and affinities for the nuclear receptor farnesoid X receptor (FXR), contributed by F. Hoffmann-La Roche. The dataset contained 102 IC50 values, spanning 6 orders of magnitude, and 36 high-resolution co-crystal structures with representatives of four major ligand classes. Strong global participation was evident, with 49 participants submitting 262 prediction submission packages in total. Procedurally, GC2 mimicked Grand Challenge 2015, with a Stage 1 subchallenge testing ligand pose prediction methods and ranking and scoring methods, and a Stage 2 subchallenge testing only ligand ranking and scoring methods after the release of all blinded co-crystal structures. Two smaller curated sets of 18 and 15 ligands were developed to test alchemical free energy methods. This overview summarizes all aspects of GC2, including the dataset details, challenge procedures, and participant results. We also consider implications for progress in the field, while highlighting methodological areas that merit continued development. Similar to Grand Challenge 2015, the outcome of GC2 underscores the pressing need for methods development in pose prediction, particularly for ligand scaffolds not currently represented in the Protein Data Bank (www.pdb.org), and in affinity ranking and scoring of bound ligands.
Keywords: D3R, docking, scoring, ligand ranking, alchemical methods, Farnesoid X Receptor, blinded prediction challenge
Introduction
The Drug Design Data Resource (D3R) is an NIH-funded resource dedicated to improving method development in ligand docking and scoring through community-wide blinded prediction challenges (http://www.drugdesigndata.org). In 2016–2017, D3R carried out Grand Challenge 2 (GC2), which focused on one comprehensive, high quality dataset for the farnesoid X receptor (FXR) target. The community engagement with this challenge was excellent, with 49 participants submitting 262 prediction sets. This overview paper summarizes the dataset, challenge submission and assessment procedures, and prediction results. We also seek to draw conclusions about the different methods used, with the goal of helping practitioners of computer-aided drug design (CADD) make more accurate predictions. A complementary set of articles from individual challenge participant labs accompanies this overview in the present special issue of the Journal of Computer-Aided Molecular Design.
Improving the accuracy of software to model protein-small molecule interactions would accelerate the expensive and time-consuming process of discovering a drug and bringing it to market. Method developers aim at improving the ability to predict the affinity (potency) of a candidate ligand, as well as its mode of interaction with the targeted protein (its binding-site pose), in order to drive rational drug design [1–3]. Ongoing efforts by many labs have generated a comprehensive and varied set of tools for CADD, but the evaluation of these tools has relied largely on retrospective studies, which are less rigorous than prospective ones. Few researchers outside of the pharmaceutical industry are in a position to carry out truly prospective predictions; and those who are tend to work on different systems and datasets, making it difficult to compare methods on a consistent footing.
The D3R project is part of a long-term initiative to enable rigorous and consistent evaluation of CADD methods, by collecting hitherto unpublished protein-ligand datasets and using them to hold blinded, community-wide prediction challenges. Our main assessment efforts revolve around ligand pose prediction, or docking; and the prediction, or at least the ranking, of ligand-protein binding potencies. The D3R continues the efforts of the Community Structure Activity Resource (CSAR) [4–8], which began in 2009. Grand Challenge 2 is the sixth community challenge under this initiative and the second carried out by D3R [9].
Grand Challenge 2 centered around a protein-ligand dataset for a bile acid receptor target, FXR, which was generated and provided by F. Hoffmann-La Roche Ltd. (Roche). Functionally, FXR forms a heterodimer with the retinoid X receptor (RXR) when activated, and then binds to hormone response elements on DNA, leading to up- or down-regulation of the expression of specific genes [10–13]. FXR agonists have been considered as potential therapeutics for dyslipidemia and diabetes [14]. The dataset contained one apo structure, and 36 co-crystal structures, with representatives from four major chemical series, as classified by Roche using the substructures portrayed in Figure S1, and with resolutions ranging from 1.8 to 2.6 Å (Table S1). The dataset also contained IC50 data for 102 compounds, from each of the four distinct chemical classes in the crystallographic structures set, along with 6 miscellaneous compounds, having a potency range spanning over 6 orders of magnitude (pM to μM) (Table S2). The FXR dataset presented multiple interesting facets for the challenge. For example, the receptor is rather flexible, as two helices adjacent to the ligand binding site can adopt varied conformations; and the binding cavity is predominantly hydrophobic, with five methionine residues in direct contact or close proximity to the ligand. In addition, some of the ligands contained ring structures with non-trivial alternative pucker conformations. Importantly, both ligand and protein conformations provided in the blinded dataset are well represented in the previously available co-crystal structures of FXR in the Protein Data Bank. At the time of challenge launch, PDB entries in the Protein Data Bank with ligands in the benzimidazole and isoxazole chemical series [15–17], but not the spirocycles or tetrahydropyrro(azo)lopyridines (formerly referred to as sulfonamides), were publicly available. This allowed us to challenge pose prediction methods for ligand classes with known and unknown structural information, an aspect that previous blinded challenges determined as a critical predictor of success [9].
The present challenge largely followed the protocols and procedures established with Grand Challenge 2015 [9]. It was held in 2 stages: in Stage 1, participants were asked to predict the ligand poses of the available crystal structures and also to predict or rank the potencies of all ligands, including those for which crystal structures were not available. As in Grand Challenge 2015, we did not specify which receptor structure to dock the ligands into, nor did we provide a “prepared” receptor (e.g., with hydrogens or with information about specific water molecules). After Stage 1 had closed, all 36 available co-crystal structures were made public. In Stage 2, participants were asked to repeat the affinity predictions or rankings, this time using the additional disclosed ligand-pose information. We additionally curated two subsets of compounds (15 tetrahydropyrro(azo)lopyridines and 18 spirocycles) that contained chemically similar compounds and thus were amenable to the calculation of relative binding affinities by “alchemical” methods [18], such as free energy perturbation (Tables S3, S4). In the following subsections, we detail the challenge dataset composition, and experimental determination and structural re-refinement procedures. We also describe the challenge, submission details and validation, and evaluation procedures. Subsequently, in the results subsection, we analyze the performance of the submitted methods for ligand pose prediction and assessment of ligand binding potency. Finally, in the discussion, we draw broad conclusions from both Grand Challenges 2015 and 2; and present future directions for blinded prediction challenges.
Materials and Methods
Composition and construction of challenge datasets
Overview of experimental dataset
The FXR dataset contributed by Roche comprised 36 previously unpublished co-crystal structures of FXR with chemically varied ligands (Table S1), one apo structure, and 102 hitherto unpublished IC50s [19] (Table S2). (All compounds are confirmed agonists, according to a cell-based functional assay not referenced in the present challenge.) The IC50 dataset includes measurements for the 36 co-crystallized ligands. Among these compounds, 96 belong to four chemical series (benzimidazoles, isoxazoles, spirocycles and tetrahydropyrro(azo)lopyridines) and six were classified as miscellaneous. For 92 of the compounds, IC50 values range from 0.000335 to 62.37 μM, while the remaining ten IC50s are listed as >100 μM. The IC50s were used in the evaluation of all affinity and ranking predictions, and were computed as the mean of replicate IC50s excluding those that resulted in undetermined IC50 value (>100 μM or > 25 μM). Some of the compounds were synthesized as racemic mixtures, diastereomers and epimers, as noted in Table S2. The crystal structures have resolutions ranging from 1.8 to 2.6 Å and contain representatives from each of the four chemical series. For ligands within the pose prediction component of the challenge (FXR 1-36), SMILES strings were distributed to participants with the stereochemistries observed in the cocrystal structures. All co-crystal structure were re-refined before release for D3R challenges and deposition into the PDB, in order to provide structures of equivalent quality across all D3R blinded challenges. This dataset of IC50s and crystal structures is available online on the D3R website (https://drugdesigndata.org/about/datasets/882). Details of the experimental studies are provided below and in the SI.
Experimental determination of IC50s
The IC50 values were determined at Roche, with a scintillation proximity radioligand displacement assay [19]. The assay buffer contained 50 mM HEPES/NaOH, pH 7.4, 10 mM NaCl, 5 mM MgCl2 and 0.01% Chaps. GST-FXR was bound to glutathione yttrium silicate SPA beads (Amersham) by shaking in a small volume of buffer at room temperature (RT), and then diluted, so that 40 nM protein and 10 mg of beads were added to each well of a 96-well plate in a volume of 100 ml. 40 nM radioligand, tritiated, 2-dicyclohexyl-2-[2-(2,4-dimethoxyphenyl)benzimidazol-1-yl]acetamide (55 Ci/mmol), was added to each well in a volume of 50 ml and the reaction incubated at RT for 30 minutes in the presence of test compounds in 50 ml buffer. The amount of radioligand remaining bound was determined by scintillation proximity counting on a Packard TopCount using Optiplates® (Perkin-Elmer). Dose response curves were obtained within a concentration range of 10−9 M to 10−4 M, and the IC50 values were obtained by fitting to these curves.
Structure determination
For crystallization, FXR constructs with surface mutations E281A and E354A were used. The ligand-FXR/co-activator complexes were formed by incubation of ~2 mg/mL FXR in 50 mM Tris/HCI pH 7.8, 100 mM NaCl, 3 mM TCEP, 1 mM EDTA, and 10% glycerol, with twelve times molar excess each of ligand and co-activator peptide. After overnight incubation at 4°C, the complexes were concentrated to ~15 mg/mL (Vivaspin 10 KD MWCO, Sartorius). Each complex was screened de novo against the Index Hampton screen at 21 °C in the sitting drop vapor diffusion setup (drop size 1 μL, protein-precipitant ratio 0.3–0.7 by volume), and initial conditions were optimized by fine-screening. A variety of crystallization conditions was identified for the different FXR-ligand complexes; these are detailed in PDB entries deposited following the close of this challenge: 5Q0K corresponding to the apo structure; and 5Q0I, 5Q12, 5Q1G, 5Q11, 5Q0Z, 5Q19, 5Q0J, 5Q0L, 5Q1H, 5Q17, 5Q1E, 5Q0W, 5Q0O, 5Q1A, 5Q0R, 5Q0T, 5Q0Q, 5Q10, 5Q13, 5Q16, 5Q1D, 5Q15, 5Q1I, 5Q0V, 5Q0S, 5Q0Y, 5Q0N, 5Q14, 5Q0P, 5Q1F, 5Q1C, 5Q18, 5Q0X, 5Q0M, 5Q0U, and 5Q1B, corresponding to structures FXR 1 to 36, respectively. For data collection at 100 K, crystals were either directly vitrified by hyperquenching [20] if their crystallization conditions contained > 20% PEG, or cryoprotected with paraffin oil prior to flash-cooling. Data were collected on either a CCD (MarResearch) or a PILATUS (Dectris) detector at Swiss Light Source beamline X10SA using X-rays of 1 Å wavelength, and were processed with either Denzo/Scalepack [21] or integrated with XDS [22] and scaled with SADABS (Bruker). The exact data collection and reduction procedures differed from crystal to crystal and are given in the deposited coordinate files. FXR structures were determined at Roche by molecular replacement with PHASER [23], using a set of previously determined in-house FXR structures as models, and the solution with the best log-likelihood gain was used as starting model for rebuilding and refinement in Refmac5 [24] or BUSTER [25].
The resulting structures, kindly contributed by Roche, were re-refined before release for D3R challenges and deposition into the PDB, in order to provide uniformity across all D3R blinded challenges. A semi-automatic procedure was used for data preparation, parameter optimization, structure refinement, and protein/ligand validation, as detailed in the SI; see also Figure S2. Overall, re-refinement led to moderate improvements in the quality of the structural models, as detailed in Table S5. The mean root mean square deviation (RMSD) between the initial models from Roche and the final re-refined models, based on superposition with CCP4’s Superpose program [26], are 0.08 Å, 0.3 Å, and 0.21 Å (minimum, maximum, and mean) for the protein components of the complexes; and 0.07 Å, 0.23 Å, 0.12 Å (minimum, maximum, and mean) for the ligands alone. The values of Rfree improved slightly, with drops of 0.01, 0.02, and 0.03 (minimum, maximum and mean) between the initial and final models.
Challenge Procedure
Posing the challenge
As noted above, GC2 followed the two-stage format of GC2015 [9]. Stage 1 opened Sep 19, 2016 and closed Nov 22, 2016; Stage 2 started once Stage 1 was closed and ended Feb 08, 2017. In both stages, participants were provided with the apo structure and 102 SMILES strings of the ligands for docking in Stage 1 and affinity prediction or ranking in both Stages 1 and 2. For pose prediction, participants were invited to submit up to five poses for each of the 36 ligands for which co-crystal structures were available (Table S1), where one of the five poses, termed Pose 1, was designated as the best guess. FXR 33 was omitted from the Stage 1 pose prediction analysis because of a discrepancy between the SMILES string provided to the participants and the crystallized ligand; specifically, the ligand used for crystallization was the N-oxide, but during crystallization a pyridine was formed, possibly during the several days it took for the crystals to grow. Additionally, when refining the N-oxide, strong negative density was present at the nominal position of the oxygen, further pointing to the absence of an N-oxide. For affinities, the full set of 102 ligands were to be ranked, including FXR 33 (Table S2). The subsets of 15 tetrahydropyrro(azo)lopyridines and 18 spirocycles designed to test explicit solvent alchemical free energy calculations are listed in Tables S3 and S4. Note that these compounds are also present in the full set of 102 which were to be scored and/or ranked by non-alchemical methods.
Submission, validation, and evaluation of predictions
Submission and basic validation of participant submissions are detailed in the SI. Predictions were evaluated as in GC2015 [9]. Thus, pose predictions were evaluated in terms of the symmetry-corrected root-mean-square deviation (RMSD) of the predicted pose relative to the crystallographic pose in the re-refined structure; potency rankings were assessed in terms of the ranking correlation statistic Kendall’s tau; and free energies were evaluated in terms of the centered root-mean-square error (RMSEc) of the predicted binding free energy differences versus those from experiment. When computing RMSD values of the predicted ligand pose relative to the crystallographic pose, we found little difference between superposition of the entire protein structure versus the binding site residues only. The present results are based on a binding site alignment script provided by the Maestro Prime Suite (align-binding-sites) that performs a secondary structure alignment of the full protein followed by an alignment using the binding site Cα atoms belonging to residues within 5 Å of the ligand atoms [27, 28]. The scripts used to evaluate the submissions are available on GitHub (https://drugdesigndata.org/about/workflows-and-scripts). Each pose prediction submission could include up to five poses, but one of the five poses. Pose 1, had to be marked as the submitter’s top pick, based, for example, on a docking score. For each submission, our primary metric for pose prediction accuracy is the median RMSD of Pose 1, across all ligands. The median was chosen because it is less sensitive to the severity of gross outliers. However, submissions were also evaluated in terms of the mean RMSD of Pose 1, across all ligands, as reflected in the Results and supplementary information. A few submissions did not provide predictions for all ligands; these were omitted from the comparative analysis provided below.
Experimental relative binding free energies are obtained from the IC50 data, based on the Cheng-Prusoff equation [29], which relates the IC50 of a competitively binding ligand L1 to its dissociation constant as follows: , where CR and Kd,R are, respectively, the concentration and dissociation constant of the displaced radioligand. The binding free energy of L1 then is given by . As a consequence, the difference in the binding free energies of two ligands of interest, L1 andL2 is , which is independent of the radioligand’s concentration and dissociation constant, as required for ligand ranking and comparisons with calculations of relative binding free energies.
The uncertainty in each value of Kendall’s tau was assessed over 10,000 rounds of bootstrap resampling with replacement, accounting also for the experimental uncertainties [9]. Experimental uncertainties are added to the free energy, ΔG, as a random offset δG drawn from a Gaussian distribution of mean zero and standard deviation RTIn(Ierr). In GC2, the value of Ierr was set to 1.5, based on the mean value of all standard deviations of each ligand’s IC50 replicate measurements (Table S2). The values of Ierr for FXR 2 and 5 were set to 3 and 10 respectively, due to their larger standard deviations, relative to other ligands.
In this dataset, 38 compounds were reported as pertaining to racemic mixtures (Table S2). For several cases where stereochemical composition was determined on chiral columns, most often a ratio of ~50:50 was observed. In addition, in several cases, the IC50s of the racemic mixture and separate enantiomers were measured and the enantiomer of interest had significantly stronger binding, with a 1–4-fold lower IC50. Therefore, for the 50:50 racemic mixtures, a factor of 2 was used to extract the IC50 of the active stereoisomer. In the beginning of the challenge, the instructions stated that participants should provide predictions that could be compared directly with the raw data. For these compounds, therefore, we have analyzed all predictions without any adjustment to the raw experimental IC50 values. The compounds treated in this manner are as follows: FXRs 37, 39, 40, 42, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 66, 67, 68, 69, 70, 71, and 72. However, by our accident, the instructions did not state that some other compounds were also tested experimentally as racemates: FXRs 6, 7, 8, 9, 13, 18, 20, 22, 25, 31, 35, and 36. For these compounds (except FXR 22), we have divided the experimental IC50 values by 2 before comparing with participant’s predictions. FXR 22 was tested as a 25:25:25:25 mixture of stereoisomers, so we have divided its experimental IC50 value by 4.
As in GC 2015, two null models were set up as performance baselines for ranking ligand potencies, and were evaluated using Kendall’s tau in the same manner as the submitted predictions. The null models are “Mwt”, in which the affinities were ranked by molecular weight; and clogP in which affinities were ranked based on the octanol–water partition coefficient estimated computationally by CDD Vault [30]. This method is based on ChemAxon’s (http://www.chemaxon.com) logP model [31].
Results
A total of 49 participants uploaded 262 prediction sets that passed basic validation tests. The numbers of valid submissions for the seven components of the challenge are listed in Table 1. It is worth noting that some submissions for the Free Energy (FE) Sets did not use the explicit solvent free energy methods envisioned for this challenge component; the numbers of alternative approaches are also listed in Table 1. The methods used for each submission are summarized in Tables S6–S16. Most participants were based in universities and institutes around the world, but there were also submissions from several pharmaceutical and software companies (Table S17). Detailed information about all submissions, including the identities of all submitters who did not elect to remain anonymous, the raw prediction and protocol files, and the corresponding performance statistics, may be found on the D3R website https://drugdesigndata.org/about/grand-challenge-2-evaluation-results). Many of the submissions considered are further discussed in articles from the participants, most or all of which are published in the same special issue as the present article. The following subsections provide a high-level analysis of the performance of the various approaches.
Table 1.
Number of validated submissions, Nsubmissions, received and number of individuals/organizations that participated, Nparticipants, for each component of D3R Grand Challenge 2. For the free energy sets, the first number indicates submissions using explicit solvent free energy methods, and the second indicates submissions using other methods.
| Challenge Component | Nsubmissions | Nparticipants |
|---|---|---|
| Pose Predictions | 51 | 33 |
| Stage 1 Affinity Rankings | 59 | 31 |
| Stage 2 Affinity Rankings | 82 | 27 |
| Stage 1 Free Energy Set 1 | 5, 9 | 3, 9 |
| Stage 1 Free Energy Set 2 | 4, 9 | 3, 9 |
| Stage 2 Free Energy Set 1 | 11, 10 | 8, 6 |
| Stage 2 Free Energy Set 2 | 10, 11 | 7, 7 |
Pose Predictions
This section examines the accuracy of pose prediction for the 35 FXR ligands for which co-crystal structures were available, FXR 1 to 32, and 34 to 36. Most of the structures belong to one of the four chemical classes (benzimidazoles, tetrahydropyrro(azo)lopyridines, spirocycles, isoxazoles), and a few are classified as miscellaneous.
Overview of methods
As summarized in Table S6, participants used a variety of methods to predict the 35 poses. Some methods focus on a single docking program, while others include multiple docking programs. Some combine docking with structure refinement via molecular dynamics simulations; others include machine learning. In addition, a number of protocol files explicitly state that the protein structures selected from the PDB for docking was based on the similarity of the challenge ligand to that of ligands in available co-crystal structures, while others do not mention using ligand similarity. A few methods did not use traditional docking at all, but instead superposed the challenge ligands onto the structures of similar ligands in available co-crystal structures.
Overview of pose prediction accuracy
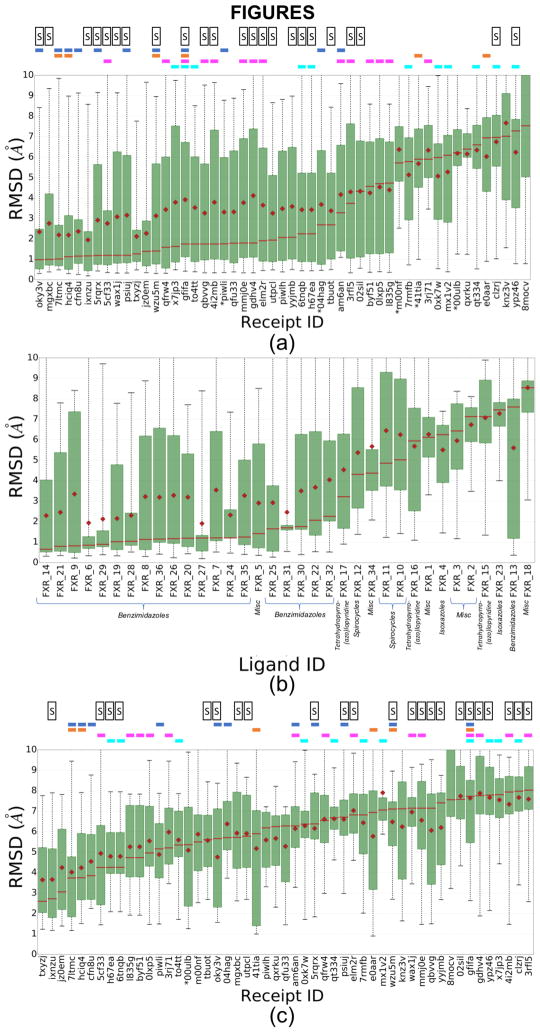
The RMSDs of all predicted poses for all 51 submissions are summarized in Fig. 1, Fig. S3 and Table 2; Fig. 1a and Fig. S3 show statistics across all ligands for each submission ordered from left to right by increasing median and mean RMSD, respectively, while Fig. 1b shows statistics across all submissions for each ligand, ordered from left to right by increasing median RMSD. In all panels, the results correspond to the top-ranked pose (Pose 1) in each submission. Many participants did well, in the sense of making predictions with a median RMSD less than 2.0 Å (Fig. 1a). All submissions tended to provide lower RMSDs for certain ligands (Fig. 1b), particularly for the benzimidazole class, as well as for the unclassified (“miscellaneous”) compound FXR 5. Substantially worse results (RMSD >3 Å) generally were obtained for the tetrahydropyrro(azo)lopyridines, spirocycles, isoxazoles, and for the unclassified ligands FXR 1, 2, 3, 18, and 34. Additionally, relatively poor results were obtained for one benzimidazole compound, FXR_13 (Fig. 1b), as further discussed below.
Figure 1.
(a) Box plots of RMSD statistics for the rank 1 poses for all 51 pose prediction submissions. (b) Box plots of RMSD statistics for all participants’ rank 1 poses, for each ligand. Each ligand’s chemical class is annotated, (c) Box plots of RMSD statistics for rank 1 poses for all 51 pose prediction submissions, including results only for ligands with Tanimoto similarities < 0.3 with ligands in publicly available FXR co-crystal structures. These compounds include the isoxazoles (FXRs 4 and 23), spiroscycles (FXRs 10, 11, and 12), tetrahydropyrro(azo)lopyridines (FXRs 15, 16, and 17), and other unclassified ligands (FXRs 1, 2, 3, and 18). Means are shown by red diamonds, the red line is for medians, the green box is for the interquartile range (IQR), and the whiskers indicate the minimum and maximum RMSDs. The results are ordered from left to right by increasing median RMSD. The colored horizontal bars above each panels (a) and (c) indicate the use of specific docking codes for each receipt ID (a unique ID given to each prediction upon submission): Glide (blue), Vina (magenta), Gold (orange), or Smina (cyan); and the letter “S” indicates if the submitted protocol file mentioned the use of ligand similarity between the challenge ligands and publicly available co-crystallized FXR ligands. Receipt IDs labeled with an asterisk did not use the full subset of ligands.
Table 2.
Union of the top 10 submissions by both median and mean RMSD of Pose 1, for the pose prediction component of the challenge, including only submissions that include the full set of ligands. (a) Results based on all ligands. (b) Results based only on ligands with Tanimoto similarities < 0.3 with ligands in publicly available FXR co-crystal structures; i.e., the isoxazoles (FXRs 4 and 23), spirocycles (FXRs 10, 11, and 12), tetrahydropyrro(azo)lopyridines (FXRs 15, 16, and 17), and other unclassified ligands (FXRs 1, 2, 3, and 18). Methods are listed in order of increasing mean RMSD.
| (a) | |||||
|---|---|---|---|---|---|
| Mean RMSD | Median RMSD | Software Used | Submitter Name | Group/PI Name | Receipt ID |
| 1.95 | 1.17 | Molsoft ICM | Polo Lam | Max Totrov | ixnzu |
| 2.12 | 1.27 | Autodock Vina, GROMACS, in-house LIE (Linear Interaction Energy Model) | Oleksandr Yakovenko | Steve Jones | txyzj |
| 2.19 | 1.02 | GLIDE, CCDC-GOLD, Amber14, MMGBSA | Yuan Hu | Merck | 7ltmc |
| 2.19 | 1.13 | Glide, Gold, Induced-fit-docking | Hongwu Wang | Merck | hciq4 |
| 2.27 | 1.39 | Wilma (flexible ligand docking algorithm), scoring function SIE (force field based scoring function) | Enrico Purisima | Enrico Purisima | jz0em |
| 2.34 | 0.99 | WaterMap, SHAPE Screening, Structural Interaction Fingerprint, DFT/B3LYP/6-31G*, GLIDE-SP-XP, Induced-fit-docking, Emodel/GlideScore-SP, Binding Pose Metadynamics | Christina Athanasiou | Zoe Cournia | oky3v |
| 2.37 | 1.16 | Glide-XP | Anonymous | Anonymo us | cfn8u |
| 2.76 | 1 | OMEGA, SHAFTS, NoDocking, Amber11 | Xiaoqin Zou | Xiaoqin Zou | mgxbc |
| 2.76 | 1.2 | Modeller, Gromacs (minimization), surflex-sim, Clusterizer and DockAccessor, Vina | Flavio Ballante | Garland R. Marshall | 5cf33 |
| 2.92 | 1.19 | ROCS, Omega, Glide-SP-XP | Ashutosh Kumar | Kam Y.J. Zhang | 5rqrx |
| 3.08 | 1.2 | MOE (most similar molecule), Confgen, Forge (alignment), Smina (minimization), Manual ranking | Matthew Baumgartner | David Evans | wax1j |
| 3.16 | 1.2 | Forge, Smina (minimization only), Glide-SP | Matthew Baumgartner | David Evans | psiuj |
| (b) | |||||
|---|---|---|---|---|---|
| Mean RMSD | Median RMSD | Software Used | Submitter Name | Group/PI Name | Receipt ID |
| 3.65 | 2.6 | Autodock Vina, GROMACS, in-house LIE (Linear Interaction Energy Model) | Oleksandr Yakovenko | Steve Jones | txyzj |
| 3.66 | 2.72 | Molsoft ICM | Maxim Totrov | Max Totrov | ixnzu |
| 4.02 | 3.74 | Smina, idock-RF-v3, Yasara (simulated annealing) | Yuan Hu | Merck | 7ltmc |
| 4.24 | 3.75 | Glide, Gold, Induced-fit-docking | Hongwu Wang | Merck | hciq4 |
| 4.25 | 3.06 | Wilma (flexible ligand docking algorithm), scoring function SIE (force field based scoring function) | Enrico Purisima | Enrico Purisima | jz0em |
| 4.54 | 3.85 | Glide-XP | Anonymous | Anonymous | cfn8u |
| 4.76 | 5.66 | WaterMap, SHAPE Screening, Structural Interaction Fingerprint, DFT/B3LYP/6-31G*, GLIDE-SP-XP, Induced-fit-docking, Emodel/GlideScore-SP, Binding Pose Metadynamics | Christina Athanasiou | Zoe Cournia | oky3v |
| 4.79 | 4.26 | Smina | Bentley Wingert | Carlos Camacho | 6tnqb |
| 4.79 | 4.26 | Smina | Bentley Wingert | Carlos Camacho | h67ea |
| 4.88 | 5.16 | Induced-fit-docking | Anonymous | Anonymous | piwli |
| 4.94 | 4.25 | Modeller, Gromacs (minimization), surflex-sim, Clusterizer and DockAccessor, Vina | Flavio Ballante | Garland R. Marshall | 5cf33 |
| 5.26 | 4.73 | AutoDock Vina, Gromacs | Pär Söderhjelm | Soderhjelm Research Group | byf51 |
Correlation of accuracy with availability of related crystal structures
Participants docked the challenge ligands into publicly available structures they selected from the PDB, so their results depend not only on their docking algorithms but also on their choice of receptor structure(s). At the time of the challenge, the PDB included co-crystal structures of FXR with ligands similar to the benzimidazoles in the challenge set, as well as to ligands FXR 5 and 34 (Canvas Tanimoto coefficient of up to 0.94 [32, 33]), whereas the similarities were below 0.3 for the remaining ligands (Table S1). As noted above, many pose-prediction methods used ligand similarity to select an appropriate FXR structure to dock each challenge ligand into (Table S6). These methods, which are marked with an “S” in Fig. 1a, are situated preferentially, though not exclusively, at the left of the graph where the RMSDs are low. One may therefore expect that the availability of co-crystal structures for ligands similar to a challenge ligand will improve pose-prediction accuracy. Indeed, the conformation of the protein binding site correlates with the ligand type. Thus, when superimposed to the apo form, the RMSDs of the challenge co-crystal structures range from 0.36 Å to 2.94 Å (Fig. S4); among these, the benzimidazoles and FXR 5 (unclassified) bind to a defined cluster of conformations that deviate from the apo structure by >2.4 Å, while the remaining ligands correspond to a less defined group of conformations that are more similar to the apo protein. As a consequence, docking into a structure that had been solved with a similar ligand may be expected to improve accuracy. The use of ligand similarity is further illustrated by two submissions (mgxbc and 5cf33) that ranked among the 10 most accurate as assessed by median RMSD (Fig. 1a), and worked by simply aligning the challenge ligands to the most similar publicly available co-crystallized FXR ligands. These observations are consistent with conclusions from Grand Challenge 2015 [9], and may explain why pose-predictions are particularly accurate for the benzimidazoles and FXR 5 for which similar compounds were present in FXR co-crystal structures, as summarized in Fig. 1b.
It is also worth examining several exceptions to the trend of better accuracy for ligands with similar compounds already in the PDB. First, although FXR 34 has a similarity coefficient of 0.83 with the ligand in available PDB structure 3W5P (Table S1), the median RMSD for this ligand across all methods was high, at 4.37 Å. Comparison of the co-crystal structures of this challenge ligand, as provided by Roche, with the structures of their most similar publicly available ligands (PDBs: 3W5P, 4QE6, and 1OT7), reveals that the maximum common substructures bind differently, and that the protein adopts significantly different conformations (Fig. S5). In this case, then, using structures solved with similar ligands to help with pose prediction may have been more misleading than helpful. However, similar observations could have been made when comparing 3W5P and 4QE6/1OT7 which could have served as a warning to participants that ligand similarity would not help in this case.
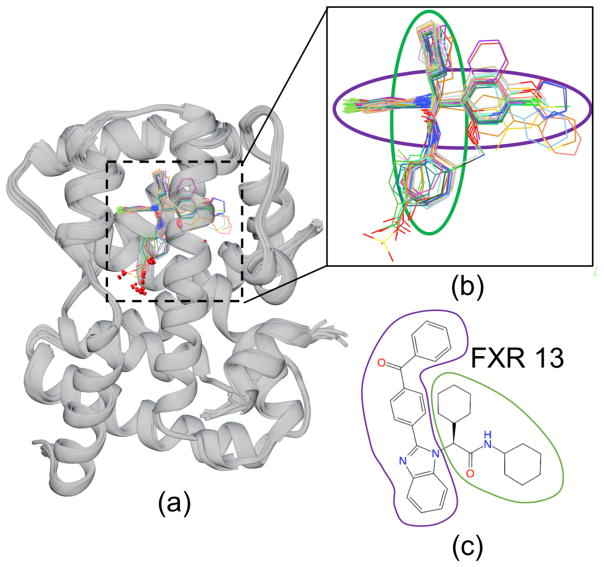
Second, unlike other compounds in its class, the benzimidazole ligand FXR 13 was handled poorly by the pose-prediction methods and resulted in an unsuccessful pose prediction performance with a high median RMSD of 7.53 Å (Fig 1b) despite having a common binding pose with the remaining ligands of the benzimidazole class (Fig 2). Comparison of FXR 13’s binding site to the remaining ligands within its class shows a lack of FXR 13-specific side chain conformational changes that would explain this inconsistency. However, its chemical structure indicates that FXR 13 has a large ligand substituent that we conjecture may cause it to be poorly handled. In addition, unlike other benzimidazole ligands with large substituents (FXR 7, FXR 9, FXR 26, FXR 36), FXR 13 has the most sterically demanding substituent; as it is more bent due to the additional carbonyl (C=O) linker and 3-dimensional structure that is essential to avoid intramolecular strain (Table S2).
Figure 2.
(a) Crystallographic poses released after Stage 1 of the benzimidazole ligands bound to FXR (gray ribbon) show a conserved binding mode within this chemotype. (b) Detailed view of the ligands without the protein. The colored ovals denote the orientations of the circled chemical groups with the groups of corresponding colors in (c). (c) Chemical drawings of ligand FXR 13 with groups circled to show the correspondence with the structural depictions in (b).
Correlation of pose prediction with docking software and method
It is of interest to inquire whether specific pose-prediction technologies performed particularly well. In order to allow, in at least an approximate manner, for statistical uncertainty in the data, Table 2 lists all 12 submissions that ranked in the top 10 based on either median or mean RMSD, in order of increasing mean RMSD. Table 2a is based on the data for all ligands, and thus corresponds to Figure 1a, while Table 2b is based only on ligands with Tanimoto similarities < 0.3 with ligands in publicly available FXR co-crystal structures, and thus corresponds to Figure 1c. The two submissions which provided both the lowest mean and median RMSD for the stringent test of predicting the poses of ligands without representative structures in the PDB (txyzj and ixnzu. Table 2b) also did well for full set of ligands (Table 2a). Interestingly, these appear to be quite different from each other, as txyzj included the use of molecular dynamics, while ixnzu used Molsoft’s ICM docking software. The other high-performing submissions listed in Table 2 span a further range of methods.
Additional patterns may be discerned by focusing on the results for several docking programs that were used by multiple participants: Glide, Gold, Smina and Vina. On first examination, methods that used Glide appear to aggregate among the top ranked methods, while those using Smina tend to rank among the bottom ranked methods. However, this pattern disappears if the graph is regenerated without the ligands for which there was no similar ligand in an existing FXR structure in the PDB (Fig. 1c). This result suggests that some of the apparent differences between software packages resulted from how they were combined with available PDB data, rather than from differences in the docking algorithms or scoring functions. Not surprisingly, when the most similar ligands are excluded from the evaluation, these methods provide no benefit, and may even perform worse than methods that ignored similarity (Fig 1c). In addition, it is clear that the accuracy obtained with a given docking code can vary, presumably depending on the details of how it is used. Unfortunately, it is difficult to ascertain which practices are most effective from these submissions, as there are many variations from one method to another.
Finally, we scanned the protocol files to identify submissions that included visual inspection as part of the prediction methodology. Unlike GC2015, where the most successful eight methods used visual inspection [9], here, none of the top eight methods mentioned visual inspection, and only two of the 26 top methods included explicit human intervention.
Predictions of ligand potency rankings
This section examines the accuracy of predicted potency rankings for the full set of 102 FXR ligands (Table S2). Results are presented for Stage 1, before the release of co-crystal structures for 35 of these ligands; and for Stage 2, following the release of these structures. These structures include instances with at least one ligand in each major chemotype (benzimidazoles, spirocycles, tetrahydropyrro(azo)lopyridines), which have conserved binding motifs and constitute 92 out of the 102 ligands.
Overview of methods
A total of 59 and 82 submissions in Stages 1 and 2, respectively, used several methods to predict affinity ranking of the full set of 102 FXR ligands. These include two different technical approaches, structure-based and ligand-based. A wide range of methods was used for structure based approaches, spanning predictions based on force field with implicit solvent models, electronic structure methods with implicit solvent models, and methods that combined physical models and machine learning; while only a few ligand-based approaches were used, spanning pure Quantitative Structure-Activity Relationships (QSAR) models, and others that combine ligand binding pose data.
Overview of potency ranking accuracy
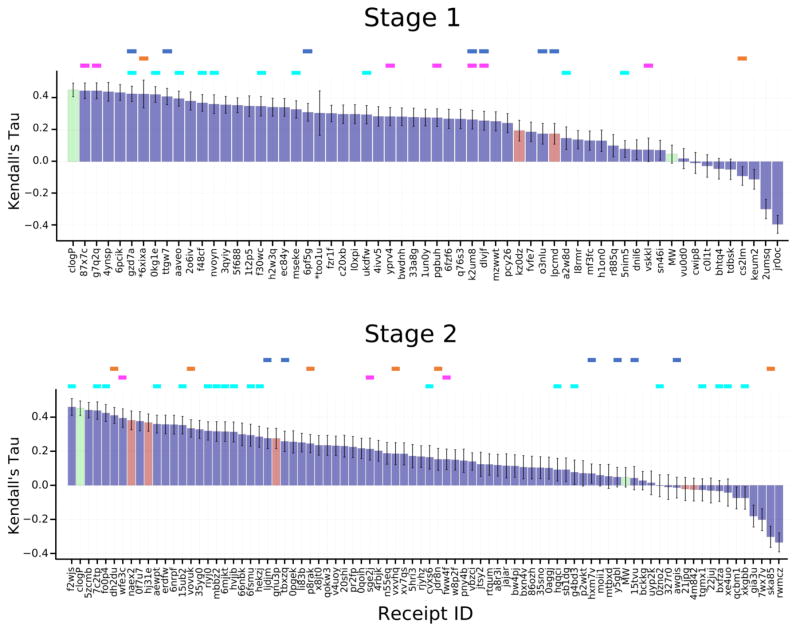
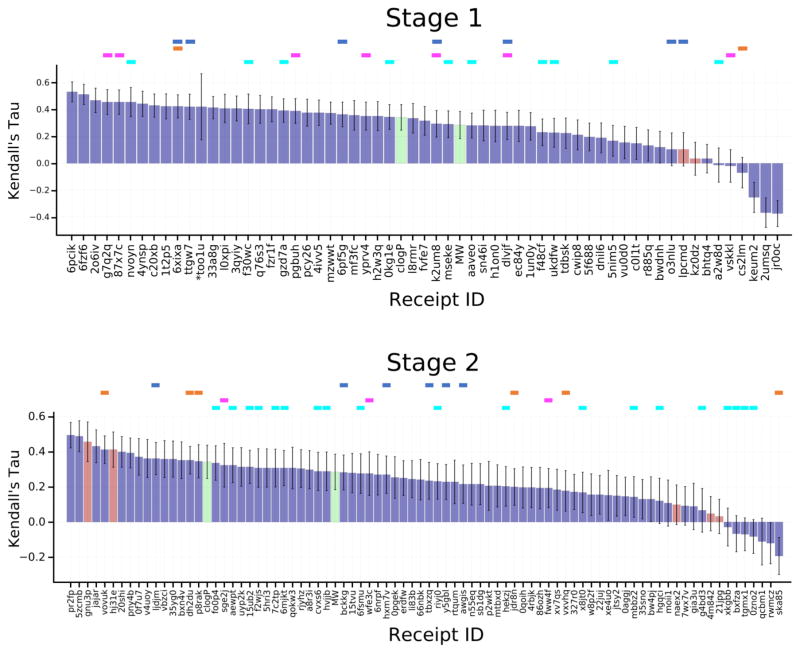
Most of the predicted rankings correlate positively with the experimental rankings, with values of Kendall’s tau up to 0.45 and 0.46 in Stages 1 and 2, respectively (Figure 3, Tables S7, S8), which is indicative of the predictive power of most of the methods used. Still, there is room for improvement, as a simple null model in which potency ranked by clogP has a Kendall’s tau of 0.45, and an ideal method which yielded the exact experimental IC50 values would have a Kendall’s tau of 0.91, after bootstrap averaging over experimental uncertainties. However, the predictions perform much better than a null model ranking ligands by molecular weight (tau = 0.05). In comparing the various submissions, it is important to keep in mind that the values of tau have uncertainties averaging 0.06, based on bootstrap sampling with replacement, which also accounts for the estimated experimental uncertainties.
Figure 3.
Kendall’s tau ranking correlation coefficients between predicted IC50 rankings and experimental IC50 rankings. Purple columns are for structure-based scoring, red bars are for ligand-based scoring, and green bars are for the null models where ligands are ranked based on molecular weight (MW) and the computed logarithm of the partition coefficient between n-octanol and water (clogP), as indicated in the axis labels. The colored horizontal bars above the columns indicate the use of specific docking codes for each receipt: Glide (blue), Vina (magenta), MMGB/SA (orange), Smina (cyan). Note that a number of methods used none of these software packages. Receipt IDs labeled by an asterisk did not use the full set of challenge ligands. The error bars are 1σ confidence intervals based on 10,000 bootstrap samples.
Relationship of ranking accuracy with technical approach and software used
Although most submissions used a structure-based approach (Fig. 3, purple columns) to rank the ligands, and only a few used a ligand-based approach (Fig. 3, red columns), it is not clear that these performed significantly differently from the structure-based methods. For example, submission naex2, a QSAR method which was trained with publicly available data on FXR ligands, achieved a Kendall’s tau of 0.38 in Stage 2, and was thus essentially within uncertainty of the top-performing structure-based methods from both stages. The top performing methods from both approaches, ligand- and structure-based methods, are listed in Table 3. The majority of methods include conventional scoring functions such smina, Vina, and Glide, the IChem-GRIM and HYDE scoring methods, and idock. It is also of interest to examine whether any particular class of structure-based method provided particularly good results. As evident from the color-coded bars in Figure 3, and detailed in Tables S7 and S8, submissions using a given software package and/or the MMGB/SA approach yielded varied levels of accuracy, depending on the details of the method, and no particular class or software package stands out across multiple submissions.
Table 3.
Top 10 submissions as ranked in order of decreasing Kendall’s tau for the affinity component of the challenge in Stages 1 and 2.
| stage 1 | ||||
|---|---|---|---|---|
| Kendall’s Tau | Software Used | Submitter Name | Group/PI Name | Receipt ID |
| 0.44 | AutoDock Vina | Olivier Bequignon | In silico Drug Design Master | g7q2q |
| 0.44 | AutoDock Vina | Doha Naga | In silico Drug Design Master | 87x7c |
| 0.44 | Ichem-GRIM, HYDE | Didier Rognan | Didier Rognan | 4ynsp |
| 0.43 | idock-RF-v3* | Ho Leung Ng | Ho Leung Ng | 6pcik |
| 0.43 | Smina | Matthew Baumgartner | David Evans | gzd7a |
| 0.43 | Glide, Gold, Amber-MMGBSA | Yuan Hu | Merck | 6xixa |
| 0.42 | Smina | Bentley Wingert | Carlos Camacho | 0kg1e |
| 0.41 | Glide | Ashutosh Kumar | Kam Y.J. Zhang | ttgw7 |
| 0.40 | Smina* | Matthew Baumgartner | David Evans | aaveo |
| 0.38 | Ichem-GRIM, HYDE | Didier Rognan | Didier Rognan | 2o6iv |
| Stage 2 | ||||
|---|---|---|---|---|
| Kendall’s Tau | Software Used | Submitter Name | Group/PI Name | Receipt ID |
| 0.46 | Smina | Bentley Wingert | Carlos Camacho | f2wjs |
| 0.44 | Rhodium HTS | Jonathan Bohmann | Pharm. & Bioeng. Dept. | 5zcmb |
| 0.44 | Smina | Bentley Wingert | Carlos Camacho | 7c2tp |
| 0.42 | Smina | Bentley Wingert | Carlos Camacho | fo0p4 |
| 0.41 | SeeSAR, HYDE, MMGBSA | Anonymous | Anonymous | dh2du |
| 0.39 | Vina | David Koes | David Koes | wfe3c |
| 0.38 | In-house QSAR script | Matthew Baumgartner | David Evans | naex2 |
| 0.38 | PRODIGY webserver | Alexandre Bonvin | Alexandre Bonvin | 0f7u7 |
| 0.37 | In-house QSAR script | Matthew Baumgartner | David Evans | hj31e |
| 0.36 | Smina | Bentley Wingert | Carlos Camacho | aewpt |
Relationship between affinity ranking accuracy and pose prediction
Perhaps surprisingly, availability of accurate ligand poses did not in general lead to more accurate affinity rankings. Stage 2 affinity rankings were not, overall, more accurate than Stage 1 affinity rankings, even though crystallographic poses had been revealed for several ligands in each of the three main chemotypes (benzimidazole, spirocycles, tetrahydropyrro(azo)lopyridines), which together accounted for 92 of the 102 ligands. To examine this issue further, we recalculated the Stage 2 Kendall’s tau values for all submissions, this time using only the 35 ligands for which crystallographic poses had been provided (FXR 1 to FXR 36). These results, summarized in Fig. 4, demonstrate that affinity rankings were not improved even when the crystallographic pose of every ligand was available. Despite having released the structures to participants for Stage 2, it wasn’t clear from their protocols whether they had actually made use of the crystal structures in Stage 2. Thus, to investigate further, we emailed participants to ask whether they actually used the crystal structures. Of the eight who replied, five had, and three had not. In some cases, this was because the structural information was irrelevant to the method. However, one participant (Receipt ID 0f7u7) re-ran his ranking method retrospectively for all 102 ligands using the structures and reported a rise in Kendall’s tau from 0.37 to 0.43. Thus, the lack of improvement between Stages 1 and 2 may reflect non-use of the released structures for various reasons.
Figure 4.
Kendall’s tau correlation coefficient scores between predicted scores and experimental binding affinities for ligands FXR 1 to FXR 36, for which co-crystal structures were released at the end of Stage 1. See Figure 3 for details.
We furthermore considered whether affinity predictions might be better for the 47 benzimidazoles, the class of ligands for which the pose prediction methods were most successful (see above). However, the maximum values of tau for this class were 0.33 and 0.36, for Stages 1 and 2, respectively (Fig S6), which is lower than the maximum values for the full compound set (Figure 3). (The tau values for the other ligand classes considered on their own (Figures S7, S8) also are lower than those for the full compound set.)
Binding free energy methods
There is considerable interest today in simulation-based methods of computing absolute and relative binding free energies [34–41]. Such methods involve computing the reversible work of artificially interconverting the ligands of interest, and may have difficulty if two ligands are very different from each other. They also are relatively time-consuming. To facilitate evaluation of such methods, we identified two subsets of the full 102-ligand set such that alchemical transformations within each set should be feasible (Figure 5). Here, we characterize the results of free energy methods applied to these sets, and compare the performance of the free energy methods with that of the other classes of methods that were applied to the full set of 102 ligands.
Figure 5.
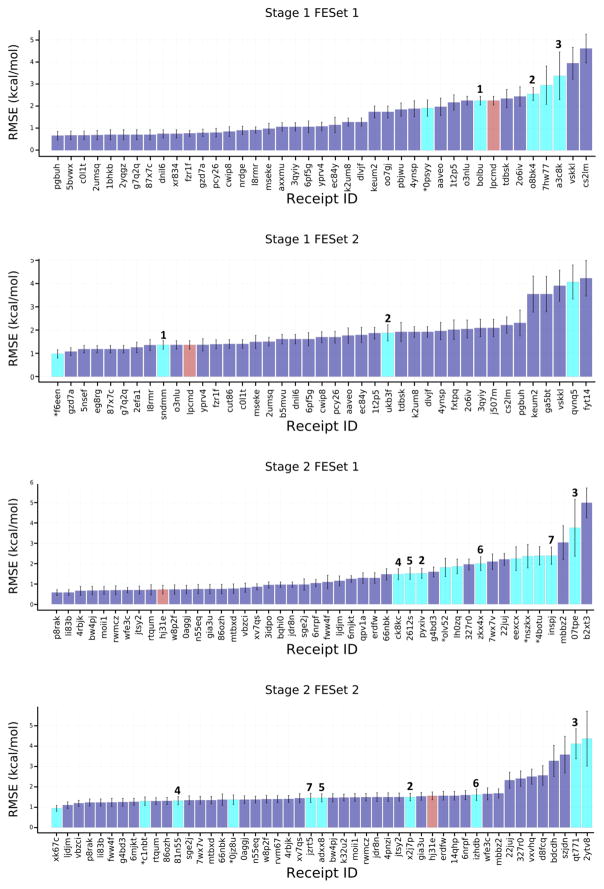
RMSEc values for the compounds in the free energy prediction sets. Purple bars are for structure-based scoring with free energy estimates, red bars are for ligand-based scoring with free energy estimates, and cyan bars are for methods using explicit solvent alchemical free energy simulations except for receipt ID xk67c which is an absolute free energy calculation method. The purple bars include scoring methods submitted to the free energy component of the challenge, as well as scoring methods with free energy estimates submitted to the affinity ranking component of the challenge. Receipt IDs that resulted in an RMSEc greater than 5 Å have been omitted for clarity. Free energy methods that appear to be identical are numbered to allow tracking across stages and FE sets. Receipt IDs labeled with an asterisk did not use the full set of FE ligands. The error bars are 1σ confidence intervals based on 10,000 bootstrap samples.
Overview of methods
A total of 30 submissions used explicit solvent free energy methods across the two challenge Stages and the two FE sets (Table 1). All of these were alchemical approaches, which provided relative binding free energies between pairs of ligands, except for one (xk67c), which computed the separate binding free energy of each separate ligand. In addition, a total of 39 submissions applied other approaches to the FE sets (Table 1); these included methods based on scoring functions, force fields combined with implicit solvent, and electronic structure calculations with implicit solvent (Tables S9–S16). Importantly, the two FE Sets are part of the full series of 102 ligands, for which a variety of additional methods were tested. This meant that we could extract the predictions for the FE Sets of compounds from the larger set of ranking and scoring methods used for the 102 compound set, and thus put the more detailed free energy methods into the context of the faster methods that were applied to the full set of 102 ligands.
Overall evaluation
We focus initially on the ability of the free energy methods to replicate measured differences in ligand binding free energies, estimated as for ligands a and b. The deviations from experiment, reported in terms of the centered RMSE (RMSEc, see Methods), range from about 1 to 4 kcal/mol (cyan columns in Figure 5). Even considering the uncertainty in the error metrics, better accuracy is achieved for FE Set 2, in both Stages 1 and 2. This difference is not explainable by methodological differences between the two sets, as several specific methods show greater accuracy for FE Set 2 than for FE Set 1; e.g, MC Pro (Method 1 in Fig 5). Additional cases where a given method could be tracked between FE Sets are also marked with numbers above each corresponding column. However, as in the case of ligand ranking (above), no clear improvement is observed on going from Stage 1 to Stage 2, for both FE sets. Perhaps surprisingly, the explicit-solvent free energy methods (Fig 5, cyan columns) did not appear to provide greater overall accuracy than the other methods that were applied to these sets (Fig. 5, purple and red columns). As detailed in Table 4, methods which performed well across both FE Sets included those based on the Autodock Vina energy score [42], a trained random forest model, and MMGB/SA methods trained on available FXR binding data.
Table 4.
Top 10 submissions in terms of RMSEc, in order of increasing RMSEc, for the two free energy sets in both stages of the challenge. Error bars are illustrated in Fig. 5 and listed in Tables S7–S12. Methods include predictions from scoring methods with free energy estimates in the affinity ranking component of the challenge, and free energy methods in the free energy component of the challenge. Methods in bold are common methods submitted by the same participant across FE sets.
| Stage 1 | ||||
|---|---|---|---|---|
| FE Set 1 | ||||
| RMSEc | Software Used | Submitter Name | Group/PI Name | Receipt ID |
| 0.66 | CDOCKER (pose prediction) + Autodock Vina (scoring) | Xinqiang Ding | Charles L. Brooks III | pgbuh |
| 0.68 | In-house machine learning score | Anonymous | Anonymous | c0l1t |
| 0.68 | In-house machine learning score | Anonymous | Anonymous | 5bvwx |
| 0.69 | SILCS approximate FE method | Sirish Lakkaraju | Alexander D MacKerell Jr. | 2umsq |
| 0.70 | Vina | doha naga | In silico Drug Design Master | 1bhkb |
| 0.70 | Vina | Olivier Bequignon | In silico Drug Design Master | 2yqgz |
| 0.70 | AutoDock Vina | doha naga | In silico Drug Design Master | 87x7c |
| 0.70 | AutoDock Vina | Olivier Bequignon | In silico Drug Design Master | g7q2q |
| 0.75 | In-house machine learning score | Anonymous | Anonymous | xr834 |
| 0.75 | In-house machine learning score | Anonymous | Anonymous | dnil6 |
| FE Set 2 | ||||
| RMSEc | Software Used | Submitter Name | Group/PI Name | Receipt ID |
| 0.98 | FESetup (Automating Setup for Alchemical Free Energy Simulations) with average network analysis | Julien Michel | Julien Michel | f6een |
| 1.07 | Smina | Matthew Baumgartner | David Evans | gzd7a |
| 1.18 | AutoDock Vina | doha naga | In silico Drug Design Master | 87x7c |
| 1.18 | AutoDock Vina | Olivier Bequignon | In silico Drug Design Master | g7q2q |
| 1.18 | Vina | Olivier Bequignon | In silico Drug Design Master | 5nsef |
| 1.18 | Vina | doha naga | In silico Drug Design Master | eg8rg |
| 1.25 | Quasi exact method FE method | Bentley Wingert | Carlos Camacho | 2efa1 |
| 1.35 | LIE (Linear Interaction Energy Model) | Oleksandr Yakovenko | Steve Jones | l8rmr |
| 1.36 | MCPro (Monte Carlo free energy perturbation) | Zhaoping Xiong | Mingyue Zheng | sndmm |
| 1.36 | Glide-XP | Zhaoping Xiong | Mingyue Zheng | lpcmd |
| Stage 2 | ||||
|---|---|---|---|---|
| FE Set 1 | ||||
| RMSEc | Software Used | Submitter Name | Group/PI Name | Receipt ID |
| 0.57 | Trained MMGB/SA | Maxim Totrov | Max Totrov | p8rak |
| 0.57 | Trained 3D QSAR + MMGB/SA | Maxim Totrov | Max Totrov | li83b |
| 0.66 | Trained Random Forest Model, Rl-score | Anonymous | Anonymous | 4rbjk |
| 0.67 | Trained Random Forest Model, Rl-score | Anonymous | Anonymous | bw4pj |
| 0.68 | Trained Random Forest Model, Rl-score | Anonymous | Anonymous | moii1 |
| 0.68 | SILCS approximate FE method | Sirish Lakkaraju | Alexander D MacKerell Jr. | rwmcz |
| 0.69 | Vina | David Koes | David Koes | wfe3c |
| 0.69 | Trained Random Forest Model, Rl-score | Anonymous | Anonymous | jtsy2 |
| 0.71 | Trained Random Forest Model, Rl-score | Anonymous | Anonymous | rtqum |
| 0.72 | QSAR Method | Matthew Baumgartner | David Evans | hj31e |
| FE Set 2 | ||||
| RMSEc | Software Used | Submitter Name | Group/PI Name | Receipt ID |
| 0.94 | Explicit solvent FE (Jarzynski pulling) | Oleksandr Yakovenko | Steve Jones | xk67c |
| 1.10 | Glide ensemble docking to known structure | Anonymous | Anonymous | ljdjm |
| 1.19 | Trained Linear Interaction Energy Model | Oleksandr Yakovenko | Steve Jones | vbzci |
| 1.22 | Trained 3D QSAR + MMGB/SA | Maxim Totrov | Max Totrov | li83b |
| 1.22 | Trained MMGB/SA | Maxim Totrov | Max Totrov | p8rak |
| 1.23 | AutoDock Vina with overlay docking | Flavio Ballante | Garland R. Marshall | fww4f |
| 1.24 | Smina + in-house scoring function | Andrey Voronkov | Andrey Voronkov | g4bd3 |
| 1.26 | Smina | Matthew Baumgartner | David Evans | 6mjkt |
| 1.29 | FESetup (Automating Setup for Alchemical Free Energy Simulations) with average network analysis | Julien Michel | Julien Michel | c1nbt |
| 1.30 | Trained Random Forest Model, Rl-score | Anonymous | Anonymous | rtqum |
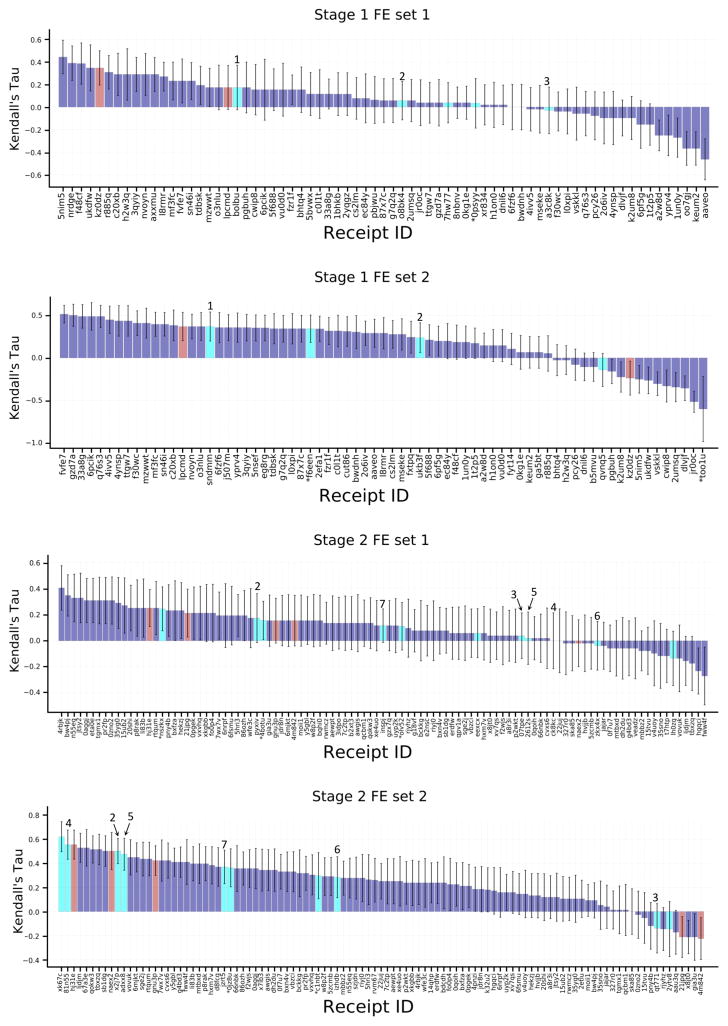
An even broader comparison of methods can be carried out by converting the binding free energy predictions for FE Sets 1 and 2 to ligand affinity rankings, computing their Kendall’s tau statistics, and putting these into the context of Kendall’s tau results for these ligand subsets extracted from the set of ranking and scoring methods used for the full sets of 102 ligands (Fig. 6). Although the error bars for these results are relatively large, due to the smaller numbers of ligands and their modest range of IC50 values, the overall picture remains much the same as reported above for the RMSEc statistics. Thus, the explicit water free energy methods (Fig 6., cyan columns) provide better rankings for FE Set 2 than FE Set 1, and the explicit solvent free energy methods do not provide clearly better ranking accuracy than other structure-based methods (Fig 6., purple columns) and ligand based methods (Fig. 6, red columns). As detailed in Table 5, only one method performed well across both FE Sets, a knowledge-based scoring function developed with a statistical mechanics-based iterative method using available FXR binding data, ITScore_v2_TF.
Figure 6.
Kendall’s tau correlation statistics between predicted scores or free energies and the experimental binding affinities for the free energy prediction set ligands. See Figure 5 for details. The purple bars here include all scoring and free energy methods.
Table 5.
Top 10 submissions in terms of Kendall’s tau, in order of increasing tau, for the two free energy sets in both stages of the challenge. Kendall’s tau error bars are illustrated in Fig. 6 and listed in Tables S13–S16. Methods include predictions from all scoring and free energy methods. Methods in bold are common methods submitted by the same participant across FE sets.
| Stage 1 | ||||
|---|---|---|---|---|
| FE Set 1 | ||||
| Kendall’s Tau | Software Used | Submitter Name | Group/PI Name | Receipt ID |
| 0.44 | Smina | Bentley Wingert | Carlos Camacho | 5nim5 |
| 0.39 | Quasi exact method FE method | Bentley Wingert | Carlos Camacho | nrdge |
| 0.39 | Smina | Bentley Wingert | Carlos Camacho | f48cf |
| 0.35 | ligand-based 3D QSAR method | Flavio Ballante | Garland R. Marshall | kz0dz |
| 0.35 | Smina | Bentley Wingert | Carlos Camacho | ukdfw |
| 0.31 | Knowledge-based scoring method ITScore_v2_TF | Xiaoqin Zou | Xiaoqin Zou | r885q |
| 0.29 | MMPB/SA | Xiaoqin Zou | Xiaoqin Zou | axxmu |
| 0.29 | MMPB/SA | Xiaoqin Zou | Xiaoqin Zou | 3qyiy |
| 0.29 | Knowledge-based scoring method ITScore_TF | Xiaoqin Zou | Xiaoqin Zou | c20xb |
| 0.29 | SeeSAR scoring function | Anonymous | Anonymous | h2w3q |
| FE Set 2 | ||||
| Kendall’s Tau | Software Used | Submitter Name | Group/PI Name | Receipt ID |
| 0.52 | Knowledge-based scoring method ITScore_v1 | Xiaoqin Zou | Xiaoqin Zou | fvfe7 |
| 0.50 | Smina | Matthew Baumgartner | David Evans | gzd7a |
| 0.49 | Knowledge-based scoring method ITScore_v2 | Xiaoqin Zou | Xiaoqin Zou | 33a8g |
| 0.49 | idock-RF-v3 scoring function with visual inspection | Ho Leung Ng | Ho Leung Ng | 6pcik |
| 0.49 | Knowledge-based scoring method ITScore_v1_TF | Xiaoqin Zou | Xiaoqin Zou | q76s3 |
| 0.45 | Knowledge-based scoring method ITScore_v2_TF | Xiaoqin Zou | Xiaoqin Zou | 4ivv5 |
| 0.44 | Ichem-GRIM score + HYDE score | Didier Rognan | Didier Rognan | 4ynsp |
| 0.44 | Glide | Ashutosh Kumar | Kam Y.J. Zhang | ttgw7 |
| 0.41 | RF-Score-VS machine learning score, Smina | Anonymous | Anonymous | f30wc |
| 0.41 | Knowledge-based scoring method ITScore_v2 | Xiaoqin Zou | Xiaoqin Zou | mzwwt |
| Stage 2 | ||||
|---|---|---|---|---|
| FE Set 1 | ||||
| Kendall’s Tau | Software Used S | submitter Name | Group/PI Name | Receipt ID |
| 0.41 | Trained Random Forest Model, Rl-Score | Anonymous | Anonymous | 4rbjk |
| 0.35 | Trained Random Forest Model, Rl-Score | Anonymous | Anonymous | bw4pj |
| 0.33 | Trained Random Forest Model, Rl-Score | Anonymous | Anonymous | jtsy2 |
| 0.33 | Trained Random Forest Model, Rl-Score | Anonymous | Anonymous | n55eq |
| 0.31 | Trained Random Forest Model, Rl-Score | Anonymous | Anonymous | 0aggj |
| 0.31 | Smina, CNN Model Scoring | David Koes | David Koes | 0zno2 |
| 0.31 | Knowledge-based scoring method ITScore_v2 | Xiaoqin Zou | Xiaoqin Zou | pr2fp |
| 0.31 | Smina, CNN Model Scoring | David Koes | David Koes | tgmx1 |
| 0.31 | QMMM energy, Schrodinger QSITE | Anonymous | Anonymous | eta0e |
| 0.29 | KRh-SCORPIO scoring function modeled using available affinity data | Jonathan Bohmann | Pharmaceuticals and Bioengineering Dept. | 35yg0 |
| FE Set 2 | ||||
| Kendall’s Tau | Software Used | Submitter Name | Group/PI Name | Receipt ID |
| 0.62 | Explicit solvent FE (Jarzynski pulling) | Oleksandr Yakovenko | Steve Jones | xk67c |
| 0.55 | QSAR method | Matthew Baumgartner | David Evans | hj31e |
| 0.55 | Schrodinger FEP | Anonymous | Anonymous | 81n55 |
| 0.53 | Glide-XP | Anonymous | Anonymous | ljdjm |
| 0.53 | Total Energy | Anonymous | Anonymous | 67a3e |
| 0.52 | Xscore | Anonymous | Anonymous | qokw3 |
| 0.52 | Glide | Ashutosh Kumar | Kam Y.J. Zhang | tbxzq |
| 0.50 | Schrodinger FEP | Christina Athanasiou | Zoe Cournia | x2j7p |
| 0.50 | QSAR method | Matthew Baumgartner | David Evans | naex2 |
| 0.50 | Knowledge-based scoring method ITScore_v1 | Xiaoqin Zou | Xiaoqin Zou | sb1dg |
Finally, it is worth noting that similar alchemical methods give quite consistent results between participants. In Stage 2, two independent groups using Schrodinger’s FEP+ achieved RMSEc values of 1.48 and 1.52 kcal/mole for FE Set 1 (Receipt IDs ck8kc and pyxiv), and 1.31 and 1.49 kcal/mol for FE set 2 (Receipt IDs 81n55 and x2j7p). It is also of interest that an absolute binding free energy method, which used a combination of Jarzynski non-equilibrium pulling and umbrella sampling (Receipt ID xk67c) performed well for Stage 2, FE Set 2, achieving an RMSEc of 0.94 kcal/mol and tau of 0.62.
Discussion
The second D3R Grand Challenge offered a venue for participants to prospectively evaluate computational methods of predicting ligand-protein poses, potency rankings, and binding free energies. Grand Challenge 2 was similar in character to the prior Grand Challenge 2015, but somewhat more tightly integrated, in tine sense that the single FXR target was used for both pose and potency predictions. In Grand Challenge 2015, the pose prediction component centered primarily on MAP4K4, while the potency predictions centered on HSP90. Participation in Grand Challenge 2 was robust, with submissions from academic labs, pharmaceutical companies, and several software development companies. A wide range of methods were used for the various challenge components, spanning ligand-based QSAR, docking and scoring, ligand overlays to existing co-crystal structures, predictions based on force fields with implicit solvent models, predictions based on electronic structure methods with implicit solvent models, methods that combined physical models and machine learning, and explicit-solvent FE methods. Many or all of the broad conclusions and themes match and reinforce what was learned in Grand Challenge 2015 (https://drugdesigndata.org/about/what-we-have-learned).
Pose predictions
Overall, participants did reasonably well at pose prediction, in the sense that about half of the submissions achieved a median RMSD of <2.0 Å for their top-ranked pose, despite the flexibility of the binding site, and its relatively featureless and hydrophobic character. However, finer-grained analysis of these results revealed that the most accurate results were obtained chiefly for ligands where pose predictions could be guided by available co-crystal structures of similar ligands with FXR. When these cases were excluded from the statistics, prediction errors rose substantially. We conclude that, in practical applications, computational chemists would be well-advised to find and fully utilize available structural data, via ligand overlays and/or selection of receptor structures solved with similar ligands. The present results also argue in favor of continued efforts to develop docking methods that can yield reliable results in the absence of model co-crystal structures, for use cases where such information is not yet available, such as in early-stage drug discovery projects. We also observed that the quality of predictions made with a given docking software can vary greatly, presumably due to other aspects of the overall methodology, such as selection and preparation of the protein structure for docking. However, the number of variations across methods makes it difficult to determine which methodologic features correlate with accuracy, aside from the use of available structural data.
One interesting difference relative to Grand Challenge 2015 concerns the role of human intervention. Whereas manual intervention was mentioned in some of the top performing pose prediction methods in the prior challenge, this was completely absent in the top ranked methods of GC2. This is, arguably, a positive step, as automation is important for replicability and ultimately to clearly delineate particular factors or methodological components that require further development.
Ranking and affinity predictions
It is encouraging that almost all submissions were far better than random at ranking the full set of ligands according their IC50 values, as evidenced by positive Kendall’s tau values ranging up to about 0.45. This broad result confirms the ability of computational methods to help guide ligand discovery. At the same time, there is considerable room for improvement in the rankings, given that a simple null model in which potency is ranked by clogP ranks among the top scoring methods, and that, even when experimental error is considered, values of tau approaching unity should, in principle, be achievable.
It is perhaps surprising that the availability of accurate poses did little or nothing to improve ranking accuracy. Thus, the Kendall’s tau values were no higher for the benzimidazole class of compounds, for which pose predictions were more accurate, than for the other classes; and the rankings of ligands FXR 1 to 36 did not improve on going from Stage 1 to Stage 2, despite the release of their crystallographic poses after Stage 1. The broad observation that pose accuracy does not clearly correlate with ranking accuracy is consistent with the results from Grand Challenge 2015, and indicates that much of the error in ligand ranking results from errors in the scoring or energy functions, as well, perhaps, as assignments of protonation states and force field limitations, rather than from failure to identify the dominant poses. This result argues for continued research and development aimed at improving this central component of CADD technologies.
It is also perhaps unexpected that explicit solvent free energy methods did not, overall, provide greater accuracy than faster, less detailed methods. This broad result, too, is consistent with Grand Challenge 2015. Explicit solvent free energy methods are promising, because they are formally correct implementations of the underlying statistical thermodynamics. Nonetheless, they may be subject to several sources of error, including incorrect assignments of protonation states, force field error, and insufficient conformational sampling. The fact that errors persist even when these methods are applied to simpler model systems, for which conformational sampling is less of an issue [43–45], suggests that further attention to protonation equilibria and force fields is still needed. In addition, the fact that methods other than free energy simulations remain strong competitors indicates that continued work on these simpler, faster approaches also can lead to advances in our ability to design potent ligands.
Directions for blinded prediction challenges
Although the current Grand Challenge format is informative and has already yielded conclusions that are consistent across two challenges, its results are still, arguably, more anecdotal than statistically compelling. This is particularly the case when it comes to evaluating specific methods, as opposed to classes of methods, because a given submission that rarely uses only a single piece of software, cannot be fully specified by even a detailed protocol, and may vary, in substantial or subtle ways, from one challenge to the next, or even from one challenge component stage to the next. We would therefore argue for a continuing effort to capture end-to-end methods in fully automated and replicable workflows, which can be shared with other researchers and subjected to continuing evaluation based on new rounds of experimental data.
As a step in this direction, we have established a rolling pose-prediction challenge, called Continuous Evaluation of Ligand Protein Predictions (CELPP; https://drugdesigndata.org/about/celpp). This challenge, which will be detailed in future publications, takes advantage of the fact that the Protein Data Bank (PDB) releases a new set of structures every week, of which roughly 50 are ligand-protein co-crystal structures suitable for pose prediction challenges. To enable CELPP and other challenges, the PDB releases data on a weekly basis in two stages. Stage I (occurring early Saturday by 3:00 UTC) provides the polymer sequences of forthcoming PDB structures, along with InChI strings for each distinct ligand, several days before Stage II full structure release at 00:00 UTC on Wednesday. An automated D3R procedure extracts suitable pose-prediction challenges from these Stage I release data, configures a data package with the required information, and sends it to servers at participating research labs. The servers carry out the docking calculations and send the predictions back to D3R, which compares the predictions with the true crystal structures as soon as the latter are released. Like the CAMEO rolling protein structure prediction exercise (CAMEO, https://www.cameo3d.org/), this procedure provides a continuing stream of evaluation data for the participating servers. These data are informative in their own right and may also be used by developers to guide methodological improvements.
Ultimately, as computational chemists develop approaches to create shareable workflows, one may envision setting up a series of promising workflows, with standardized input and output formats, at a community computer resource, and having a third party test them with newly published protein-ligand interaction data as it emerges in the scientific literature. So long as the workflows are run without human intervention, aside from feeding in the challenge data and evaluating the output predictions, this would qualify as a blinded challenge, well suited to providing statistically meaningful performance evaluations as the results accumulate. Thus, as new Grand Challenges are held, we encourage participants to work toward higher levels of automation and shareability of their workflows, to support replication and evaluation, as well as dissemination and real-world application of the most effective approaches.
Conclusions
Successful prediction of ligand-protein poses depends on the entire workflow, including factors extrinsic to the core docking algorithm, such as the conformation of the protein selected.
The accuracy of pose predictions tends to be improved by the use of available structural data, via ligand overlays and/or selection of receptor structures solved with similar ligands.
The accuracy of the poses used in structure-based affinity rankings does not clearly correlate with ranking accuracy.
Explicit solvent free energy methods did not, overall, provide greater accuracy than faster, less detailed scoring methods.
Supplementary Material
Figure S1. FXR ligand chemotypes.
Figure S2. D3R Structure Refinement Workflow. Only residues flagged in the validation report are visually checked.
Figure S3. Box plots of RMSD statistics for tine rank 1 poses for all 51 pose prediction submissions as ranked by mean RMSDs.
Figure S4. Structures of compounds FXR 1 – 36 co-crystallized with FXR from two viewpoints rotated 180° around a horizontal axis (a, b). The ribbon representations are colored by RMSD relative to the apo structure, as illustrated by the color spectrum, with more rigid regions of FXR are rendered transparent. Panel (c) lists the challenge dataset co-crystal ligands, their corresponding protein RMSD relative to the apo structure, and their chemical classes, in order of decreasing RMSD.
Figure S5. (a) Cocrystal structure of ligand FXR 34 (blue) with FXR, overlaid with FXR cocrystal structures PDBs 4QE6, 1OT7, and 3W5P (grey) (b) Chemical drawings of the ligands illustrated in (a). The atoms belonging to the maximum common ligand substructures between the ligands are circled in (b) and displayed in stick and ball representation in (a). (c) Detailed view of the ligands without the protein. RMSDs between the maximum common ligand substructures of FXR 34 and PDB ligands 3W5P, 4QE6, and 1OT7 are 6, 7, and 6.3 Å, respectively.
Figure S6. Kendall’s tau correlation coefficients between the predicted and experimental binding affinities for the benzimidazole class of ligands. Purple columns are for structure-based scoring and red bars are for ligand-based scoring. Receipt IDs labeled with an asterisk did not use the full subset of ligands. The error bars are 1σ confidence intervals based on 10,000 bootstrap samples.
Figure S7. Kendall’s tau correlation coefficients between the predicted and experimental binding affinities for the spirocycle class of ligands. See Figure S6 for details.
Figure S8. Kendall’s tau correlation coefficient scores between the predicted and experimental binding affinities for the tetrahydropyrro(azo)lopyridines class of ligands. See Figure S6 for details.
Table S1. Pose prediction dataset, showing each compound’s ID, chemical class, the resolution and free R factor of the corresponding co-crystal structures, the Tanimoto similarity coefficient of each ligand with the most similar ligand in any FXR co-crystal structure in the PDB at the start of the challenges, and the PDB IDs of these co-crystal structures. The Tanimoto similarity coefficients were calculated using linear fingerprinting from Canvas, Schrödinger [1, 2].
Table S2. FXR potency dataset showing each compound’s ID, SMILES string, 2D chemical structure generated in Maestro (Schrödinger Release 2017-2: MS Jaguar, Schrödinger, LLC, New York, NY, 2017), average experimental IC50 as outlined in the “Methods” section, replicate IC50s, information on the stereochemical composition of the compound in the assay, and chemical class. The IC50s were measured with a scintillation proximity assay as described in Methods.
Table S3. Free Energy Set 1. Each panel lists the chemical structure, Compound ID, and experimental binding free energy estimated as RT In (IC50).
Table S4. Free Energy Set 2. Each panel lists the chemical structure, Compound ID, and experimental binding free energy estimated as RT In IC50.
Table S5. D3R refinement statistics on Farnesoid-X-Receptor (FXR) X-ray structures. Work and free R-factors (Rfree) are measures of the fit of the model to a subset of the experimental data that was used in model refinement in the case of Rwork or set aside for experimental validation in the case of Rfree. The overall quality percentile indicates the percentage of PDB entries that are equal or less than the quality indicator of the structure of interest.
Table S6. Summary of results for pose prediction challenge. For each submission, the table lists the Receipt ID (a unique ID given to each prediction upon submission); the number of ligands for which pose predictions were provided; the median RMSD (Å), relative to the experimental structures, for the poses marked as the best guess across all 35 ligands (Pose 1); the median RMSD (Å) of Pose 1 predictions only for ligands with a similarity coefficient to publicly available ligands of less than 0.3 (FXRs 1, 2, 3, 4, 10, 11, 12, 15, 16, 17, 18, 23); the mean RMSD of the Pose 1 ligands relative to the experimental structures; and a list of software used, according to the protocol file, as well as other methodological notes. Also listed is whether the protocol file mentioned any use of ligand similarity between the challenge ligands and publicly available co-crystallized FXR ligands, and whether visual inspection played a role in the method.
Table S7. Kendall’s tau statistics and software used for FXR affinity ranking predictions during Stage 1. For each participant, the table lists Receipt ID, the number of ligands for which predictions were made, Kendall’s tau and Kendall’s tau uncertainty, method type (structure- vs ligand-based), and software used. Asterisks indicate the use of visual inspection.
Table S8. Kendall’s tau statistics and software used for FXR affinity ranking predictions during Stage 2. For each participant, the table lists Receipt ID, number of ligands for which predictions were made, Kendall’s tau and Kendall’s tau uncertainty, method type (structure- vs ligand-based), and software used. Asterisks indicate use of visual inspection.
Table S9. RMSEc statistics and software used for free energy predictions of FE Set 1 during Stage 1. Statistics are calculated for predictions from scoring methods with free energy estimates in the affinity ranking component of the challenge, and free energy methods in the free energy component of the challenge. For each participant, the table lists Receipt ID, number of ligands used, RMSEc and RMSEc uncertainty, method type [scoring (structure- vs ligand-based) vs alchemical methods], and software used. Asterisks indicate the use of visual inspection.
Table S10. RMSEc statistics and software used for free energy predictions of FE Set 2 during Stage 1. Statistics are calculated for predictions from scoring methods with free energy estimates in the affinity ranking component of the challenge, and free energy methods in the free energy component of the challenge. For each participant, the table lists Receipt ID, number of ligands for which predictions were made, RMSEc and RMSEc uncertainty, method type [scoring (structure- vs ligand-based) vs alchemical methods], and software used. Asterisks indicate use of visual inspection.
Table S11. RMSEc statistics and software used for free energy predictions of FE Set 1 during Stage 2. Statistics are calculated for predictions from scoring methods with free energy estimates in the affinity ranking component of the challenge, and free energy methods in the free energy component of the challenge. For each participant, the table lists Receipt ID, number of ligands for which predictions were made, RMSEc and RMSEc uncertainty, method type [scoring (structure- vs ligand-based) vs alchemical methods], and software used. Asterisks indicate the use of visual inspection.
Table S12. RMSEc statistics and software used for free energy predictions of FE Set 2 during Stage 2. Statistics are calculated for predictions from scoring methods with free energy estimates in the affinity ranking component of the challenge, and free energy methods in the free energy component of the challenge. For each participant, the table lists Receipt ID, number of ligands for which predictions were made, RMSEc and RMSEc uncertainty, method type [scoring (structure- vs ligand-based) vs alchemical methods], and software used. Asterisks indicate the use of visual inspection.
Table S13. Kendall’s tau statistics and software used for free energy predictions of FE Set 1 during Stage 1. Statistics are calculated for predictions from all scoring and free energy methods. For each participant, the table lists Receipt ID, number of ligands for which predictions were made, Kendall’s tau and Kendall’s tau uncertainty, method type [scoring (structure- vs ligand-based) vs alchemical methods], and software used. Asterisks indicate the use of visual inspection.
Table S14. Kendall’s tau statistics and software used for free energy predictions of FES Set 2 during Stage 1. Statistics are calculated for predictions from all scoring and free energy methods. For each participant, the table lists Receipt ID, number of ligands for which predictions were made, Kendall’s tau and Kendall’s tau uncertainty, method type [scoring (structure- vs ligand-based) vs alchemical methods], and software used. Asterisks indicate the use of visual inspection.
Table S15. Kendall’s tau statistics and software used for free energy predictions of FE Set 1 during Stage 2. Statistics are calculated for predictions from all scoring and free energy methods. For each participant, the table lists Receipt ID, number of ligands for which predictions were made, Kendall’s tau and Kendall’s tau uncertainty, method type [scoring (structure- vs ligand-based) vs alchemical methods], and software used. Asterisks indicate the use of visual inspection.
Table S16. Kendall’s tau statistics and software used for free energy predictions of FE Set 2 during Stage 2. Statistics are calculated for predictions from all scoring and free energy methods. For each participant, the table lists Receipt ID, number of ligands for which predictions were made, Kendall’s tau and Kendall’s tau uncertainty, method type [scoring (structure- vs ligand-based) vs alchemical methods], and software used. Asterisks indicate the use of visual inspection.
Table S17. List of non-anonymous participants and their corresponding receipt IDs.
Acknowledgments
This work was supported by National Institutes of Health (NIH) grant 1U01GM111528 for the Drug Design Data Resource (D3R). We also thank OpenEye Scientific Software for generously donating the use of their software. The contents of this publication are solely the responsibility of the authors and do not necessarily represent the official views of the NIH. MKG has an equity interest in, and is a co-founder and scientific advisor of, VeraChem LLC. REA has equity interest in and is a co-founder and scientific advisor of Actavalon, Inc., VAF has equity interest in Actavalon, Inc. and PW has an equity interest in Relay Pharmaceuticals, Inc.
References
- 1.Sliwoski G, Kothiwale S, Meiler J, Lowe EW. Computational Methods in Drug Discovery. Pharmacol Rev. 2014;66:334–395. doi: 10.1124/pr.112.007336. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Amaro RE, Baron R, McCammon JA. An improved relaxed complex scheme for receptor flexibility in computer-aided drug design. J Comput Aided Mol Des. 2008;22:693–705. doi: 10.1007/s10822-007-9159-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Jorgensen WL. The Many Roles of Computation in Drug Discovery. Science. 2004;303:1813–1818. doi: 10.1126/science.1096361. [DOI] [PubMed] [Google Scholar]
- 4.Carlson HA. Lessons Learned over Four Benchmark Exercises from the Community Structure–Activity Resource. J Chem Inf Model. 2016;56:951–954. doi: 10.1021/acs.jcim.6b00182. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Carlson HA, Smith RD, Damm-Ganamet KL, et al. CSAR 2014: A Benchmark Exercise Using Unpublished Data from Pharma. J Chem Inf Model. 2016;56:1063–1077. doi: 10.1021/acs.jcim.5b00523. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Smith RD, Damm-Ganamet KL, Dunbar JB, et al. CSAR Benchmark Exercise 2013: Evaluation of Results from a Combined Computational Protein Design, Docking, and Scoring/Ranking Challenge. J Chem Inf Model. 2016;56:1022–1031. doi: 10.1021/acs.jcim.5b00387. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Damm-Ganamet KL, Smith RD, Dunbar JB, et al. CSAR Benchmark Exercise 2011–2012: Evaluation of Results from Docking and Relative Ranking of Blinded Congeneric Series. J Chem Inf Model. 2013;53:1853–1870. doi: 10.1021/ci400025f. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Smith RD, Dunbar JB, Ung PM-U, et al. CSAR Benchmark Exercise of 2010: Combined Evaluation Across All Submitted Scoring Functions. J Chem Inf Model. 2011;51:2115–2131. doi: 10.1021/ci200269q. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Gathiaka S, Liu S, Chiu M, et al. D3R grand challenge 2015: Evaluation of protein–ligand pose and affinity predictions. J Comput Aided Mol Des. 2016;30:651–668. doi: 10.1007/S10822-016-9946-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Makishima M, Okamoto AY, Repa JJ, et al. Identification of a Nuclear Receptor for Bile Acids. Science. 1999;284:1362–1365. doi: 10.1126/science.284.5418.1362. [DOI] [PubMed] [Google Scholar]
- 11.Parks DJ, Blanchard SG, Bledsoe RK, et al. Bile Acids: Natural Ligands for an Orphan Nuclear Receptor. Science. 1999;284:1365–1368. doi: 10.1126/science.284.5418.1365. [DOI] [PubMed] [Google Scholar]
- 12.Wang H, Chen J, Hollister K, et al. Endogenous Bile Acids Are Ligands for the Nuclear Receptor FXR/BAR. Mol Cell. 1999;3:543–553. doi: 10.1016/S1097-2765(00)80348-2. [DOI] [PubMed] [Google Scholar]
- 13.Lu TT, Makishima M, Repa JJ, et al. Molecular Basis for Feedback Regulation of Bile Acid Synthesis by Nuclear Receptors. Mol Cell. 2000;6:507–515. doi: 10.1016/S1097-2765(00)00050-2. [DOI] [PubMed] [Google Scholar]
- 14.Gardès C, Blum D, Bleicher K, et al. Studies in mice, hamsters, and rats demonstrate that repression of hepatic apoA-I expression by taurocholic acid in mice is not mediated by the farnesoid-X-receptor. J Lipid Res. 2011;52:1188–1199. doi: 10.1194/jlr.M012542. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Richter HGF, Benson GM, Bleicher KH, et al. Optimization of a novel class of benzimidazole-based farnesoid X receptor (FXR) agonists to improve physicochemical and ADME properties. Bioorg Med Chem Lett. 2011;21:1134–1140. doi: 10.1016/j.bmcl.2010.12.123. [DOI] [PubMed] [Google Scholar]
- 16.Richter HGF, Benson GM, Blum D, et al. Discovery of novel and orally active FXR agonists for the potential treatment of dyslipidemia & diabetes. Bioorg Med Chem Lett. 2011;21:191–194. doi: 10.1016/j.bmcl.2010.11.039. [DOI] [PubMed] [Google Scholar]
- 17.Feng S, Yang M, Zhang Z, et al. Identification of an N-oxide pyridine GW4064 analog as a potent FXR agonist. Bioorg Med Chem Lett. 2009;19:2595–2598. doi: 10.1016/j.bmcl.2009.03.008. [DOI] [PubMed] [Google Scholar]
- 18.Tembre BL, Mc Cammon JA. Ligand-receptor interactions. Comput Chem. 1984;8:281–283. doi: 10.1016/0097-8485(84)85020-2. [DOI] [Google Scholar]
- 19.Nichols JS, Parks DJ, Consler TG, Blanchard SG. Development of a Scintillation Proximity Assay for Peroxisome Proliferator-Activated Receptor y Ligand Binding Domain. Anal Biochem. 1998;257:112–119. doi: 10.1006/abio.1997.2557. [DOI] [PubMed] [Google Scholar]
- 20.Warkentin M, Thorne RE. A general method for hyperquenching protein crystals. J Struct Funct Genomics. 2007;8:141–144. doi: 10.1007/s10969-007-9029-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Otwinowski Z, Minor W. [20] Processing of X-ray diffraction data collected in oscillation mode. Methods Enzymol. 1997;276:307–326. doi: 10.1016/S0076-6879(97)76066-X. [DOI] [PubMed] [Google Scholar]
- 22.Kabsch W. XDS. Acta Crystallogr D Biol Crystallogr. 2010;66:125–132. doi: 10.1107/S0907444909047337. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.McCoy AJ, Grosse-Kunstleve RW, Adams PD, et al. Phaser crystallographic software. J Appl Crystallogr. 2007;40:658–674. doi: 10.1107/S0021889807021206. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Winn MD, Murshudov GN, Papiz MZ. Macromolecular TLS Refinement in REFMAC at Moderate Resolutions. Methods Enzymol. 2003;374:300–321. doi: 10.1016/50076-6879(03)74014-2. [DOI] [PubMed] [Google Scholar]
- 25.Blanc E, Roversi P, Vonrhein C, et al. Refinement of severely incomplete structures with maximum likelihood in BUSTER-TNT. Acta Crystallogr D Biol Crystallogr. 2004;60:2210–2221. doi: 10.1107/S0907444904016427. [DOI] [PubMed] [Google Scholar]
- 26.Krissinel E, Henrick K. Secondary-structure matching (SSM), a new tool for fast protein structure alignment in three dimensions. Acta Crystallogr D Biol Crystallogr. 2004;60:2256–2268. doi: 10.1107/S0907444904026460. [DOI] [PubMed] [Google Scholar]
- 27.Jacobson MP, Pincus DL, Rapp CS, et al. A hierarchical approach to all-atom protein loop prediction. Proteins Struct Funct Bioinforma. 2004;55:351–367. doi: 10.1002/prot.10613. [DOI] [PubMed] [Google Scholar]
- 28.Jacobson MP, Friesner RA, Xiang Z, Honig B. On the Role of the Crystal Environment in Determining Protein Side-chain Conformations. J Mol Biol. 2002;320:597–608. doi: 10.1016/S0022-2836(02)00470-9. [DOI] [PubMed] [Google Scholar]
- 29.Yung-Chi C, Prusoff WH. Relationship between the inhibition constant (KI) and the concentration of inhibitor which causes 50 per cent inhibition (I50) of an enzymatic reaction. Biochem Pharmacol. 1973;22:3099–3108. doi: 10.1016/0006-2952(73)90196-2. [DOI] [PubMed] [Google Scholar]
- 30.Ekins S, Bunin B. The Collaborative Drug Discovery (CDD) Database. In: Kortagere S, editor. Silico Models for Drug Discovery. Humana Press; 2013. pp. 139–154. [DOI] [PubMed] [Google Scholar]
- 31.Viswanadhan VN, Ghose AK, Revankar GR, Robins RK. Atomic physicochemical parameters for three dimensional structure directed quantitative structure-activity relationships. 4. Additional parameters for hydrophobic and dispersive interactions and their application for an automated superposition of certain naturally occurring nucleoside antibiotics. J Chem Inf Comput Sci. 1989;29:163–172. doi: 10.1021/ci00063a006. [DOI] [Google Scholar]
- 32.Duan J, Dixon SL, Lowrie JF, Sherman W. Analysis and comparison of 2D fingerprints: Insights into database screening performance using eight fingerprint methods. J Mol Graph Model. 2010;29:157–170. doi: 10.1016/j.jmgm.2010.05.008. [DOI] [PubMed] [Google Scholar]
- 33.Sastry M, Lowrie JF, Dixon SL, Sherman W. Large-Scale Systematic Analysis of 2D Fingerprint Methods and Parameters to Improve Virtual Screening Enrichments. J Chem Inf Model. 2010;50:771–784. doi: 10.1021/ci100062n. [DOI] [PubMed] [Google Scholar]
- 34.Kuhn B, Tichý M, Wang L, et al. Prospective Evaluation of Free Energy Calculations for the Prioritization of Cathepsin L Inhibitors. J Med Chem. 2017;60:2485–2497. doi: 10.1021/acs.jmedchem.6b01881. [DOI] [PubMed] [Google Scholar]
- 35.Keränen H, Pérez-Benito L, Ciordia M, et al. Acylguanidine Beta Secretase 1 Inhibitors: A Combined Experimental and Free Energy Perturbation Study. J Chem Theory Comput. 2017;13:1439–1453. doi: 10.1021/acs.jctc.6b01141. [DOI] [PubMed] [Google Scholar]
- 36.Lenselink EB, Louvel J, Forti AF, et al. Predicting Binding Affinities for GPCR Ligands Using Free-Energy Perturbation. ACS Omega. 2016;1:293–304. doi: 10.1021/acsomega.6b00086. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Abel R, Mondal S, Masse C, et al. Accelerating drug discovery through tight integration of expert molecular design and predictive scoring. Curr Opin Struct Biol. 2017;43:38–44. doi: 10.1016/j.sbi.2016.10.007. [DOI] [PubMed] [Google Scholar]
- 38.Chipot C. Frontiers in free-energy calculations of biological systems. Wiley Interdiscip Rev Comput Mol Sci. 2014;4:71–89. doi: 10.1002/wcms.1157. [DOI] [Google Scholar]
- 39.Aldeghi M, Heifetz A, Bodkin MJ, et al. Accurate calculation of the absolute free energy of binding for drug molecules. Chem Sci. 2015;7:207–218. doi: 10.1039/C5SC02678D. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Aldeghi M, Heifetz A, Bodkin MJ, et al. Predictions of Ligand Selectivity from Absolute Binding Free Energy Calculations. J Am Chem Soc. 2017;139:946–957. doi: 10.1021/jacs.6b11467. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Mishra SK, Calabró G, Loeffler HH, et al. Evaluation of Selected Classical Force Fields for Alchemical Binding Free Energy Calculations of Protein-Carbohydrate Complexes. J Chem Theory Comput. 2015;11:3333–3345. doi: 10.1021/acs.jctc.5b00159. [DOI] [PubMed] [Google Scholar]
- 42.Trott O, Olson AJ. AutoDock Vina: Improving the speed and accuracy of docking with a new scoring function, efficient optimization, and multithreading. J Comput Chem. 2010;31:455–461. doi: 10.1002/jcc.21334. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Bannan CC, Burley KH, Chiu M, et al. Blind prediction of cyclohexane–water distribution coefficients from the SAMPL5 challenge. J Comput Aided Mol Des. 2016;30:927–944. doi: 10.1007/s10822-016-9954-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Yin J, Henriksen NM, Slochower DR, et al. Overview of the SAMPL5 host–guest challenge: Are we doing better? J Comput Aided Mol Des. 2017;31:1–19. doi: 10.1007/s10822-016-9974-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Muddana HS, Fenley AT, Mobley DL, Gilson MK. The SAMPL4 host–guest blind prediction challenge: an overview. J Comput Aided Mol Des. 2014;28:305–317. doi: 10.1007/s10822-014-9735-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Figure S1. FXR ligand chemotypes.
Figure S2. D3R Structure Refinement Workflow. Only residues flagged in the validation report are visually checked.
Figure S3. Box plots of RMSD statistics for tine rank 1 poses for all 51 pose prediction submissions as ranked by mean RMSDs.
Figure S4. Structures of compounds FXR 1 – 36 co-crystallized with FXR from two viewpoints rotated 180° around a horizontal axis (a, b). The ribbon representations are colored by RMSD relative to the apo structure, as illustrated by the color spectrum, with more rigid regions of FXR are rendered transparent. Panel (c) lists the challenge dataset co-crystal ligands, their corresponding protein RMSD relative to the apo structure, and their chemical classes, in order of decreasing RMSD.
Figure S5. (a) Cocrystal structure of ligand FXR 34 (blue) with FXR, overlaid with FXR cocrystal structures PDBs 4QE6, 1OT7, and 3W5P (grey) (b) Chemical drawings of the ligands illustrated in (a). The atoms belonging to the maximum common ligand substructures between the ligands are circled in (b) and displayed in stick and ball representation in (a). (c) Detailed view of the ligands without the protein. RMSDs between the maximum common ligand substructures of FXR 34 and PDB ligands 3W5P, 4QE6, and 1OT7 are 6, 7, and 6.3 Å, respectively.
Figure S6. Kendall’s tau correlation coefficients between the predicted and experimental binding affinities for the benzimidazole class of ligands. Purple columns are for structure-based scoring and red bars are for ligand-based scoring. Receipt IDs labeled with an asterisk did not use the full subset of ligands. The error bars are 1σ confidence intervals based on 10,000 bootstrap samples.
Figure S7. Kendall’s tau correlation coefficients between the predicted and experimental binding affinities for the spirocycle class of ligands. See Figure S6 for details.
Figure S8. Kendall’s tau correlation coefficient scores between the predicted and experimental binding affinities for the tetrahydropyrro(azo)lopyridines class of ligands. See Figure S6 for details.
Table S1. Pose prediction dataset, showing each compound’s ID, chemical class, the resolution and free R factor of the corresponding co-crystal structures, the Tanimoto similarity coefficient of each ligand with the most similar ligand in any FXR co-crystal structure in the PDB at the start of the challenges, and the PDB IDs of these co-crystal structures. The Tanimoto similarity coefficients were calculated using linear fingerprinting from Canvas, Schrödinger [1, 2].
Table S2. FXR potency dataset showing each compound’s ID, SMILES string, 2D chemical structure generated in Maestro (Schrödinger Release 2017-2: MS Jaguar, Schrödinger, LLC, New York, NY, 2017), average experimental IC50 as outlined in the “Methods” section, replicate IC50s, information on the stereochemical composition of the compound in the assay, and chemical class. The IC50s were measured with a scintillation proximity assay as described in Methods.
Table S3. Free Energy Set 1. Each panel lists the chemical structure, Compound ID, and experimental binding free energy estimated as RT In (IC50).
Table S4. Free Energy Set 2. Each panel lists the chemical structure, Compound ID, and experimental binding free energy estimated as RT In IC50.
Table S5. D3R refinement statistics on Farnesoid-X-Receptor (FXR) X-ray structures. Work and free R-factors (Rfree) are measures of the fit of the model to a subset of the experimental data that was used in model refinement in the case of Rwork or set aside for experimental validation in the case of Rfree. The overall quality percentile indicates the percentage of PDB entries that are equal or less than the quality indicator of the structure of interest.
Table S6. Summary of results for pose prediction challenge. For each submission, the table lists the Receipt ID (a unique ID given to each prediction upon submission); the number of ligands for which pose predictions were provided; the median RMSD (Å), relative to the experimental structures, for the poses marked as the best guess across all 35 ligands (Pose 1); the median RMSD (Å) of Pose 1 predictions only for ligands with a similarity coefficient to publicly available ligands of less than 0.3 (FXRs 1, 2, 3, 4, 10, 11, 12, 15, 16, 17, 18, 23); the mean RMSD of the Pose 1 ligands relative to the experimental structures; and a list of software used, according to the protocol file, as well as other methodological notes. Also listed is whether the protocol file mentioned any use of ligand similarity between the challenge ligands and publicly available co-crystallized FXR ligands, and whether visual inspection played a role in the method.
Table S7. Kendall’s tau statistics and software used for FXR affinity ranking predictions during Stage 1. For each participant, the table lists Receipt ID, the number of ligands for which predictions were made, Kendall’s tau and Kendall’s tau uncertainty, method type (structure- vs ligand-based), and software used. Asterisks indicate the use of visual inspection.
Table S8. Kendall’s tau statistics and software used for FXR affinity ranking predictions during Stage 2. For each participant, the table lists Receipt ID, number of ligands for which predictions were made, Kendall’s tau and Kendall’s tau uncertainty, method type (structure- vs ligand-based), and software used. Asterisks indicate use of visual inspection.
Table S9. RMSEc statistics and software used for free energy predictions of FE Set 1 during Stage 1. Statistics are calculated for predictions from scoring methods with free energy estimates in the affinity ranking component of the challenge, and free energy methods in the free energy component of the challenge. For each participant, the table lists Receipt ID, number of ligands used, RMSEc and RMSEc uncertainty, method type [scoring (structure- vs ligand-based) vs alchemical methods], and software used. Asterisks indicate the use of visual inspection.
Table S10. RMSEc statistics and software used for free energy predictions of FE Set 2 during Stage 1. Statistics are calculated for predictions from scoring methods with free energy estimates in the affinity ranking component of the challenge, and free energy methods in the free energy component of the challenge. For each participant, the table lists Receipt ID, number of ligands for which predictions were made, RMSEc and RMSEc uncertainty, method type [scoring (structure- vs ligand-based) vs alchemical methods], and software used. Asterisks indicate use of visual inspection.
Table S11. RMSEc statistics and software used for free energy predictions of FE Set 1 during Stage 2. Statistics are calculated for predictions from scoring methods with free energy estimates in the affinity ranking component of the challenge, and free energy methods in the free energy component of the challenge. For each participant, the table lists Receipt ID, number of ligands for which predictions were made, RMSEc and RMSEc uncertainty, method type [scoring (structure- vs ligand-based) vs alchemical methods], and software used. Asterisks indicate the use of visual inspection.
Table S12. RMSEc statistics and software used for free energy predictions of FE Set 2 during Stage 2. Statistics are calculated for predictions from scoring methods with free energy estimates in the affinity ranking component of the challenge, and free energy methods in the free energy component of the challenge. For each participant, the table lists Receipt ID, number of ligands for which predictions were made, RMSEc and RMSEc uncertainty, method type [scoring (structure- vs ligand-based) vs alchemical methods], and software used. Asterisks indicate the use of visual inspection.
Table S13. Kendall’s tau statistics and software used for free energy predictions of FE Set 1 during Stage 1. Statistics are calculated for predictions from all scoring and free energy methods. For each participant, the table lists Receipt ID, number of ligands for which predictions were made, Kendall’s tau and Kendall’s tau uncertainty, method type [scoring (structure- vs ligand-based) vs alchemical methods], and software used. Asterisks indicate the use of visual inspection.
Table S14. Kendall’s tau statistics and software used for free energy predictions of FES Set 2 during Stage 1. Statistics are calculated for predictions from all scoring and free energy methods. For each participant, the table lists Receipt ID, number of ligands for which predictions were made, Kendall’s tau and Kendall’s tau uncertainty, method type [scoring (structure- vs ligand-based) vs alchemical methods], and software used. Asterisks indicate the use of visual inspection.
Table S15. Kendall’s tau statistics and software used for free energy predictions of FE Set 1 during Stage 2. Statistics are calculated for predictions from all scoring and free energy methods. For each participant, the table lists Receipt ID, number of ligands for which predictions were made, Kendall’s tau and Kendall’s tau uncertainty, method type [scoring (structure- vs ligand-based) vs alchemical methods], and software used. Asterisks indicate the use of visual inspection.
Table S16. Kendall’s tau statistics and software used for free energy predictions of FE Set 2 during Stage 2. Statistics are calculated for predictions from all scoring and free energy methods. For each participant, the table lists Receipt ID, number of ligands for which predictions were made, Kendall’s tau and Kendall’s tau uncertainty, method type [scoring (structure- vs ligand-based) vs alchemical methods], and software used. Asterisks indicate the use of visual inspection.
Table S17. List of non-anonymous participants and their corresponding receipt IDs.