Abstract
Neuropsychiatric disorders have been demonstrated to manifest shape differences in cortical structures. Labeled Cortical Distance Mapping (LCDM) is a powerful tool in quantifying such morphometric differences and characterizes the morphometry of the laminar cortical mantle of cortical structures. Specifically, LCDM data are distances of labeled gray matter (GM) voxels with respect to the gray/white matter cortical surface. Volumes and descriptive measures (such as means and variances for each subject) based on LCDM distances provide descriptive summary information on some of the shape characteristics. However, additional morphometrics are contained in the data and their analysis may provide additional clues to underlying differences in cortical characteristics. To use more of this information, we pool (merge) LCDM distances from subjects in the same group. These pooled distances can help detect morphometric differences between groups, but do not provide information about the locations of such differences in the tissue in question. In this article, we check for the influence of the assumption violations on the analysis of pooled LCDM distances. We demonstrate that the classical parametric tests are robust to the non-normality and within sample dependence of LCDM distances and nonparametric tests are robust to within sample dependence of LCDM distances. We specify the types of alternatives for which the tests are more sensitive. We also show that the pooled LCDM distances provide powerful results for group differences in distribution of LCDM distances. As an illustrative example, we use GM in the ventral medial prefrontal cortex (VMPFC) in subjects with major depressive disorder (MDD), subjects at high risk (HR) of MDD, and healthy subjects. Significant morphometric differences were found in VMPFC due to MDD or being at HR. In particular, the analysis indicated that distances in left and right VMPFCs tend to decrease due to MDD or being at HR, possibly as a result of thinning. The methodology can also be applied to other cortical structures.
Keywords: computational anatomy, depression, laminar cortical mantle, morphometry, ventral medial prefrontal cortex
1 Introduction
In the past 15 years, the laminar structure of the neo-cortex has received considerable attention thanks to advances in high resolution magnetic resonance imaging (MRI) technology and the development of Computational Anatomy (CA) methods (e.g., [3, 7, 13, 15, 17, 19]). Specifically, Labeled Cortical Distance Mapping (LCDM) has been shown to be a powerful tool for structural comparison of cortical thickness characteristics in the cingulate cortex in studies of Alzheimer’s disease and schizophrenia [1, 16, 25].
LCDM characterizes the morphometry of the laminar cortical mantle. The term “morphometry” here has two components, the structural formation (like surface and form) of the tissue and scale or size (like volume and surface area). Thus, morphometry refers to all aspects of laminar shape, where “shape” refers to the surface structure, while “size” refers to the scale of the tissue in question. Specifically, LCDM data are distances of labeled gray matter (GM) voxels with respect to the gray/white matter (GM/WM) cortical surface. Hence LCDM distances are local measures characterizing the morphometry of the cortical mantle.
In this article, we assess the use of pooling of LCDM distances in discriminating between diagnostic groups. In particular we consider LCDM data for the Ventral Medial Prefrontal Cortex (VMPFC) which is implicated in major depressive disorders (MDD) [10-14]. Abnormalities have been demonstrated in structure and function of the prefrontal cortex due to MDD [10, 11]. Other structural imaging studies have largely focused on adult onset MDD, while only few have focused on early onset MDD. Structural deficits in a subregion of the VMPFC, i.e., subgenual prefrontal cortex, have also been associated with early onset of MDD [2].
Previously, we analyzed morphometric measures (i.e., volume and descriptive summary statistics based on LCDM distances such as median, mode, range, and variance) and demonstrated that except for left-right asymmetry and correlation between left and right measures, these variables usually failed to discriminate between MDD and healthy groups [5]. This may be due to the fact that the subjects are age-matched female twins, whose VMPFC may be similar in size. This might also be partly due to the small sample size (i.e., number of subjects). On the other hand, by only using a descriptive summary statistic (such as volume or median) of the numerous distances for each person, we essentially lose most of the information provided by LCDM measures. Therefore, we suggest a strategy to avoid such information loss and to more fully utilize the shape or morphometric characteristics contained in the data by using all of the LCDM distances. Along these lines, we pool (i.e., merge) the LCDM distances by condition or group and use the pooled distances to detect morphometric differences. However the pooled distances do not have within sample independence, as the distances of neighboring voxels of each voxel are dependent. Moreover, there is also dependence between distances in left and right VMPFC in each subject, as they belong to the same person. But we demonstrate that within sample dependence does not affect the tests in terms of empirical significance levels (or Type I errors) or power. Throughout the article, we use α=0.05 as the significance level to declare a p-value to be significant.
We describe the acquisition of LCDM distances in Section 2.1, the methods we employ in Sections 2.2 and 2.3, present the analysis of pooled distances in Section 3, and investigate the influence of assumption violations in Section 4.
2. Methods
2.1 Data Description and Acquisition
A cohort of 34 right-handed young female twin pairs between the ages of 15 and 24 years old were obtained from the Missouri Twin Registry in order to study cortical changes in the VMPFC associated with MDD. The inclusion criteria for affected twin pairs were onset prior to age 16 and the DSM-IV criteria for MDD being greater than duration of 4 weeks. Control twin pairs had no personal or first degree of family history of MDD. Both monozygotic and dizygotic twin pairs were included, of which 14 pairs were controls (Ctrl) and 20 pairs had one twin affected with MDD, their co-twins were designated as the HR group. Three high resolution T1-weighted MPRAGE magnetic resonance scans of each subject in this population were acquired using a Siemens scanner with 1 mm3 isotropic resolution. Images were then averaged, corrected for intensity inhomogeneity and interpolated to 0.5×0.5×0.5 mm3 isotropic voxels. Following [23], a region of interest (ROI) comprising the VMPFC stripped of the basal ganglia, eyes, sinus, cavity, was defined manually and segmented into gray matter (GM), white matter (WM), and cerebrospinal fluid (CSF) by Bayesian segmentation using the expectation maximization algorithm [12]. A triangulated representation of the cortex at the GM/WM boundary was generated using isocontouring algorithms [12].
Bayesian segmentation [12] automatically segments the tissue via the Expectation-Maximization minimization of Gaussians for the three tissue classes at each voxel. Partial volume i.e. voxels that share mixtures were resolved via a Neymann-Pearson recalibration of the segmentation based on a training set [23]. The threshold between GM and WM was used to generate a triangulated isosurface via the marching tetrahedra algorithm i.e. the mesh is dense. Validation with several VMPFC subvolumes yielded misclassification errors of 0.05-0.10 (n=5) for the segmentation and sub-voxel accuracy of the isosurface with 50 percent of the vertices within 0.12-0.28 mm (n=14) from semi-automated contours [23].
LCDM is generated as follows: first, the ROI subvolume is partitioned by a regular lattice of voxels of specific size h , denoted V(h). Every voxel is labeled by tissue type as gray matter (GM), white matter (WM), or cerebrospinal fluid (CSF) (see, e.g., [12, 17]). For every GM voxel in the ROI, the distance from the centroid of the voxel to the closest point on GM/WM surface is computed. Let S(Δ) be the triangulated graph representing the GM/WM surface. An LCDM distance is a set distance function d : νi ∈ V(h) → d (νi , S(Δ)), the distance between the centroid of voxel νi and the set S(Δ) ; that is, it is the distance from the center of the voxel to the closest vertex on the surface. More precisely,
| (1) |
where CM (·) stands for center of mass (or centroid), and ∥·∥2 is the usual L2 – norm . We use a signed (or labeled) distance to indicate the location of each voxel with respect to the GM/WM surface. Figure 1 illustrates the computation of distances between labeled voxels and the cortical surface; also shown is the corresponding non-normalized histograms of LCDM distances. Observe that GM tissue comprises most of the cortex, and by construction, while most of GM distances are positive, most of WM distances are negative, and all of CSF distances are positive. Negative distances for some GM close to the GM/WM boundary are possible by construction, because the surface is constructed in such a way that a surface is always intersecting voxels, i.e., partial volume. So some appropriately labeled GM voxels may fall on a side of surface that they should not belong to. However, these mislabeled voxels constitute a small proportion of all voxels and do not affect the overall analysis. Reliability of LCDMs is dependent on GM segmentation and reconstruction of GM/WM surfaces which has been validated for several cortical structures including VMPFC [23], cingulate cortex [24, 25] and planum temporale [22]. Condensing to a single distance value for each vertex on the surface is the next logical step in extending LCDM. This is called Local LCDM or LLCDM and is useful in comparing thickness across multiple subjects for a cortical structure (see [20, 21]).
Figure 1.
A two-dimensional illustration of normal distances from a GM and a WM voxel to the GM/WM surface (left) and non-normalized histograms of LCDM distances of GM, WM, and CSF tissues (right).
For the left ROI, let DL be the set of LCDM distances, be the distance calculated as in Equation (1) and associated with kth voxel in subject j in group i for k = 1, 2,…,Kij , j = 1, 2,…,ni and i = 1, 2,3 (here group 1 is for MDD, 2 is for HR, and 3 is for Ctrl). Thus, n1 = 20, n2 = 20, and n3 = 28. Right distances DR are denoted similarly as . Based on prior anatomical knowledge (e.g., [14]), cortical thickness of the VMPFC is roughly 6 mm, so we can safely retain distances between −0.5 mm and 5.5 mm so that (potentially) mislabeled GM is excluded from the data. In this particular case for the left and right VMPFC, only 0.16% and 0.14% of distances were below −0.5 mm respectively; similarly, only 0.22% and 0.07% of distances were above 5.5 mm , respectively.
2.2 Pooling LCDM Distances by Group
Although the descriptive measures such as mean, median, and variance of LCDM distances are global measures regarding the morphometry of VMPFC, they are summary statistics (such as volume or median), so they tend to oversimplify the data since instead of a large number of LCDM distances per subject, we will have two (e.g., one mean value for left, one for right VMPFC) measures for each subject [5]. Hence we lose most of the information conveyed by the LCDM distances. A solution to this problem is using all the LCDM distances in our analysis. So we pool LCDM distances of subjects from the same group and thereby obtain yet another global measure of morphometry. That is, we pool the LCDM distances for all left MDD VMPFCs, those for all left HR VMPFCs, and those for all left Ctrl VMPFCs. Likewise, we pool the right VMPFC LCDM distances. Thus, for left VMPFCs
| (2) |
where is the ℓth distance in group i and is the number of distances (i.e., GM voxels) in group i for i = 1, 2,3 (group 1 is for MDD, group 2 for HR, and group 3 for Ctrl). Similarly, we denote the right pooled distances as . Furthermore, we denote the overall (i.e., groups combined) pooled left and right distances as and , respectively. See Table 1 for the corresponding sample sizes, means, and standard deviations of the pooled LCDM distances, overall and for each group. For pooling the LCDM distances, the most crucial assumption is that the subjects with the same diagnosis have similar VMPFC in morphometry, which is reasonable in practice. By pooling, the most common characteristics of the VMPFC specific to a diagnostic group are emphasized, while the differences at the individual (i.e., subject) level are downplayed. Furthermore, the pooled distances will be more powerful in detecting the differences between LCDM distances (hence differences in morphometry).
Table 1.
The sample sizes (n), means, medians, and standard deviations (SD) of the pooled LCDM distances (in mm) for left and right VMPFCs categorized by group
| Left VMPFCs | Right VMPFCs | |||||||
|---|---|---|---|---|---|---|---|---|
| Group | n | mean | median | SD | n | mean | median | SD |
| MDD | 238937 | 1.62 | 1.46 | 1.13 | 170534 | 1.63 | 1.49 | 1.10 |
| HR | 228224 | 1.61 | 1.46 | 1.11 | 216978 | 1.59 | 1.46 | 1.08 |
| Ctrl | 308498 | 1.66 | 1.50 | 1.14 | 293479 | 1.66 | 1.53 | 1.12 |
| Overall | 775659 | 1.63 | 1.48 | 1.13 | 680991 | 1.63 | 1.50 | 1.10 |
2.3 Statistical Tests
There is an inherent dependence between LCDM distances of voxels to the gray matter/white matter boundary due to spatial correlation at the level of individual subjects. When we pool the LCDM distances by group, this spatial dependence is not removed. That is, pooling neither creates nor removes the inherent dependence of the distances, as it only ignores the subject information. We compare the distributions and central measures (e.g., means) of the LCDM distances using various statistical tests. In particular, we consider Kruskal-Wallis (K-W) test for omnibus multi-group comparison of the LCDM distributions and ANOVA F-tests for omnibus multi-group comparison of the LCDM means. For k groups the null hypothesis for K-W test is H0 : F1 = F2 =…=Fk where Fi is the distribution function of group i and the null hypothesis for ANOVA F-test is H0 : μ1 = μ2 =…=μk where μi is the mean of group i, for i = 1, 2,…,k. For comparison of distributions of LCDM distances of pairs of groups, we apply Wilcoxon rank sum test and Kolmogorov-Smirnov (K-S) tests; and for comparisons of means of pairs of LCDM distance groups, we apply Welch’s t-test (see [8] for more detail on these tests). For pairwise comparisons, Wilcoxon rank sum test is done as a post hoc test after a significant K-W test, because Wilcoxon rank sum and K-W tests are both variants of the same test for multiple or two group comparison. K-S test is performed to determine the stochastic ordering. Wilcoxon rank sum test (also called the Mann–Whitney U test) is a non-parametric test for assessing whether two independent samples of observations have similar values. It is based on the sum of the ranks of the two independent samples, when the samples are pooled together. Under the null hypothesis, it is assumed that the distributions of both groups are equal, i.e., H0 : F1 = F2 . In other words, the probability of an observation from the first population being larger than the one from the second population is the same as the probability of an observation from the second population being larger than the first. For two groups, the K-S test is a nonparametric test based on the estimated maximum difference between the cumulative distributions of the two groups. Under the null hypothesis, it is assumed that the distributions are equal, i.e., H0 : F1 = F2 . Welch’s t-test is an extension of the usual Student’s t-test and is intended for use with two samples having (possibly) unequal variances. The null hypothesis for Welch’s t-test is H0 : μ1 = μ2 .
Wilcoxon and t-tests imply an ordering in a location parameter such as mean or median. Stochastic ordering, if present, can be deduced from the direction of the alternative, together with the graph of the cumulative distribution functions (cdfs). However, we can also use Kolmogorov-Smirnov (K-S) tests for H0 : F1 = F2 . Although Wilcoxon rank sum and K-S tests have the same null hypothesis, Wilcoxon test gives an overall distribution comparison based on the rankings of the observations, while K-S test compares the cdfs of the observations at values where the maximum differences between cdfs occur. Hence Wilcoxon test can be significant for only one of the one-sided alternatives, while K-S test yields p-values that are not complementary for the one-sided alternatives (i.e., they don’t add up to 1). Hence, p-values can be significant for both or none of the directional alternatives. This results from the fact that, the order of the cdfs F1 and F2 can be different at different distance values (plotted on the horizontal axis). Moreover, if p-value based on K-S test is significant for only one-sided alternative, then we can also deduce stochastic ordering. The p-values being insignificant or significant for both one-sided alternatives imply lack of stochastic ordering. But the first case implies that equality of the distributions is retained, while the latter implies that the distributions are different. Although K-S test does not provide the actual values where the significant differences between cdfs occur, it is more informative and suggestive of distributional differences compared to Wilcoxon rank sum test. Furthermore, different cdf orderings at different values can be masked by the Wilcoxon rank sum test. Hence K-S test is more informative compared to Wilcoxon rank sum test.
We perform the omnibus multi-group tests before the pairwise comparison tests, because if a multi-group test is not significant, there is no need to perform the pairwise tests. For example, if K-W test is not significant, then the distributions of the LCDM distances of groups are not significantly different, hence Wilcoxon rank sum test on each pair of groups is redundant. On the other hand, if a multi-group test yields a significant result, it only means that there are some significant differences between the groups, but does not indicate which groups are different. To determine the pairs that have significant difference, we have to perform the pairwise comparison methods. Among the tests we consider, K-W and ANOVA F-tests are omnibus tests, and Wilcoxon rank sum and Welch’s t-tests are for commonly used multiple comparison procedures after obtaining a significant omnibus test result. Rejecting an omnibus test for k groups suggest that there are differences between some pair(s) of the groups, and to determine which pair(s) exhibit significant differences, k(k – 1)/2 pairwise comparisons are needed. Hence, for large k values, an omnibus test might save a great deal of time and energy since after an insignificant omnibus test, there is no need for the pairwise tests. For small k values, one might do an omnibus test followed by pairwise tests, or just the pairwise tests directly. However, for even k=4, we need 6 pairwise tests, and this might still be too many pairwise tests, if omnibus test were insignificant.
For the nonparametric tests (K-W, Wilcoxon rank sum, and K-S tests) only within sample independence is violated, but for the parametric tests (ANOVA F-tests and t-test), the assumptions of normality (i.e., Gaussianity) and within sample independence are violated. See [4] for a complete list of assumptions for each of these tests. However, we investigate the influence of assumption violations on both nonparametric and parametric tests in Section 4 by an extensive Monte Carlo simulation study where we find the effect of assumption violations is negligible and we conjecture that this is due to the fact that the correlation structure is similar for each person (hence for each group). Moreover, our analysis does not concern inference for single populations but comparison of multiple populations. Given the difficulty to develop a method that accounts for spatial correlations, we ignore this type of spatial dependence henceforth.
In the analysis of the pooled distances, we apply classical parametric and nonparametric tests to detect the differences in LCDM distances due to diagnostic group factors. Such differences will imply morphometric changes (if any) due to the particular disease in question. K-W test provides an overall test of distributional equality for multiple groups. That is, if K-W test yields a significant p-value, then we conclude that LCDM distances are different in distribution for at least two groups, but it does not indicate which pair or pairs of groups exhibit differences. To find out which pairs exhibit significant distributional differences, we apply Wilcoxon rank sum test for each pair of LCDM groups. On the other hand, K-S test is only applicable to compare the distributions of two LCDM groups. Similarly, if an ANOVA F-test yields a significant p-value, it implies that the mean LCDM distances are different for at least two LCDM distance groups. To find out which pairs exhibit significant mean differences, we apply Welch’s t-test for each pair of LCDM groups. The p-values for the t-test and Wilcoxon rank sum test are complementary, in the sense that p-values for the one-sided alternatives add up to 1 and can be significant for only one of the one-sided alternatives. Hence, Wilcoxon test provides an overall distributional comparison for two LCDM groups. On the other hand, p-values for K-S test are not complementary, as they do not add up to 1 for the one-sided alternatives. For example, one might have significant p-values for both of the one-sided alternatives, which implies that at a particular distance value, a group’s empirical cumulative distribution function (ecdf) is significantly larger, while at another distance value the other group’s ecdf is larger. Wilcoxon test (together with the ecdf plots) and K-S tests (either with p-values for both one-sided tests or with the ecdf plots) might provide the stochastic ordering (if present) of pooled distances.
3 Analysis of Pooled LCDM Distances
First we test for any distributional differences between the LCDM distances of the three diagnostic groups by K-W test and apply the ANOVA F-tests (with or without assuming homogeneity of variances (HOV)) for the equality of the means of the left and right LCDM distances of the three groups. The null hypothesis for these tests are provided in Section 2.3 (see also [4]).
The left and right pooled distances for each group are significantly non-normal (i.e., their distributions are significantly different from a Gaussian distribution) where based on Lilliefor’s test of normality p < .0001 for each test (see, e.g., [38]), due to the heavy right skew of the densities. This skew is biologically reasonable since most of the gray matter voxels will be expected to be near the GM/WM surface. Moreover, HOV is rejected ( p < .0001 for both left and right pooled distances based on B-F test). Hence nonparametric tests of group comparisons would be more appropriate for this data. However, our Monte Carlo simulation results (see Section 4) suggest that both parametric and nonparametric tests are appropriate, with each being more sensitive for different alternatives.
The hypothesis of equality of the distributions of the pooled distances can be attributed to the similarity in the VMPFC shapes for all groups, but not vice versa (i.e., the equality of the distributions does not necessarily imply morphometric similarity, but only similarity in the distance structure of GM tissue with respect to the GM/WM surface). Notice that LCDM distances analyzed in this fashion provide morphometric information, on cortical mantle thickness and shape because the comparison is done on the ranking of distances (for K-W test) and means of the distances (for ANOVA F-tests) with respect to the GM/WM surface. For example, suppose two VMPFC tissues are composed of 100 and 1000 voxels of similar proportional distances, and then the test will detect no difference, although the morphometry is obviously different. Hence, as long as the voxels are at a similar distance from the GM/WM surface, their abundance will not influence the test results. That is, these tests are “independent of sample density” of LCDM distances.
The resulting p-values are presented in Table 2. Observe that there are significant differences between the LCDMs of the three groups, i.e., the distributions (and hence the means) of the LCDM distances for at least two groups are significantly different. Hence we conclude that there are significant morphometric differences in both left and right VMPFCs of at least two of the diagnostic groups in question. Hence, we perform pairwise comparisons by Wilcoxon rank sum test and Welch’s t-test for left (and right) distances, using Holm’s correction for multiple comparisons. In fact, we could start with pairwise tests directly, since we have only three diagnostic groups. However, for completeness and generality, we follow the more conventional path with an omnibus multi-group test followed by pairwise tests. The simultaneous hypotheses for Wilcoxon tests for left pooled LCDM distances are
| (3) |
The less-than alternative for pairwise Wilcoxon tests is then
| (4) |
Notice that if, for example, MDD left distances tend to be smaller than HR left distances, then the corresponding distribution functions have the opposite order, i.e., . Hence the left sided (i.e., less than) alternative for LCDM distances implies that MDD pooled distances tend to be smaller than Ctrl pooled distances, and HR pooled distances tend to be smaller than Ctrl pooled distances and MDD pooled distances tend to be smaller than HR pooled distances. The greater than alternatives are similar except the inequalities should be reversed. Then we adjust these p-values for simultaneous comparisons by Holm’s correction method for each alternative. We perform a similar analysis for right pooled distances.
Table 2.
The p-values for the multi-group comparisons of the pooled LCDM distances by K-W test, ANOVA F-tests with and without HOV. pKW : p-value for K-W test, pF1 , pF2 : p-values for ANOVA F-tests with and without HOV, respectively
| Multi-group Comparisons of the Pooled Distances | |
|---|---|
| Left | Right |
| pKW < .0001 , pF1 < .0001 , pF2 < .0001 | pKW < .0001 , pF1 < .0001 , pF2 < .0001 |
The null hypotheses for pairwise t-tests are similar to the ones provided in (3) and (4) with F being replaced by μ and the inequalities reversed.
We present the p-values in Table 3. Observe that the distributions of LCDM distances for MDD and HR groups are not significantly different for both left and right VMPFCs (p-values based on Wilcoxon rank sum test are .3022 and .0776, respectively). On the other hand, mean LCDM distances for MDD subjects are significantly larger than that for HR subjects for both left and right VMPFCs (p-values based on t-test are .0383 and .0041, respectively). This seemingly contradictory situation occurs since the LCDM distances are highly skewed right. The LCDM distances for both MDD and HR left VMPFCs tend to be significantly smaller than those of Ctrl left VMPFCs. The same holds for the right VMPFCs also.
Table 3.
The p-values for the simultaneous pairwise comparisons of the pooled distances by Wilcoxon rank sum test and the t-test. The p-values are adjusted by Holm’s correction method. (g, (ℓ) : first group is greater (less) than the second group.)
| With Wilcoxon rank sum test | With t-test | |||
|---|---|---|---|---|
| Pair | Left | Right | Left | Right |
| MDD, HR | .3022 ( ℓ ) | .0776 (g) | .0383 (g) | .0041 (g) |
| MDD, Ctrl | <.0001 ( ℓ ) | <.0001 ( ℓ ) | <.0001 ( ℓ ) | <.0001 ( ℓ ) |
| HR, Ctrl | <.0001 ( ℓ ) | <.0001 ( ℓ ) | <.0001 ( ℓ ) | <.0001 ( ℓ ) |
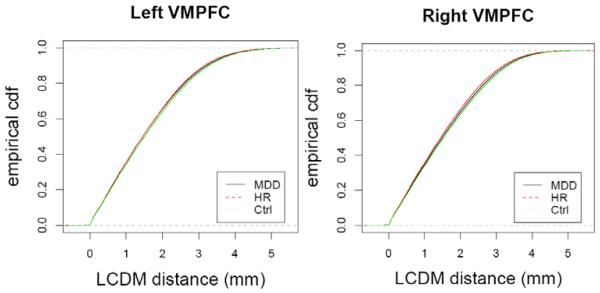
Stochastic ordering of the distances could be deduced from the direction of the alternative, together with the graph of the cdfs. See Figure 5 for the cdf plots of the pooled distances. Although K-S test do not provide the actual distance values where the significant differences between cdfs occur, it is more informative and suggestive of distributional differences than Wilcoxon tests. Furthermore, different cdf orderings at different distance values are masked by the Wilcoxon test in MDD and HR left distances. The associated p-values are presented in Table 4 where tests for the alternatives are adjusted by Holm’s correction method. Observe that the cdf of Ctrl-left distances is significantly smaller than those of MDD and HR-left distances. Furthermore, the cdfs of MDD and HR-left distances are significantly different from each other, with both sides being significant, which suggests that the order of cdf comparisons changes at different distance values. Thus, we conclude that MDD-left <ST Ctrl-left and HR-left <ST Ctrl-left where <ST stands for “stochastically smaller than”. That is, it is more likely for MDD- or HR-left distances to be smaller compared to Ctrl-left distances.
Figure 5.
Empirical cdfs of the pooled LCDM distances when extreme subjects are removed for the left and right VMPFCs.
Table 4.
The p-values for the cdf comparisons (overall and by group) of the pooled LCDM distances. The p-values for each type of alternative are adjusted by Holm’s correction method
| p-values for cdf comparisons | ||||||
|---|---|---|---|---|---|---|
| Left | Right | |||||
| Pair | 2-sided | 1st<2nd | 1st>2nd | 2-sided | 1st<2nd | 1st>2nd |
| MDD, HR | <.0001 | <.0001 | .0073 | .0316 | .0158 | .6017 |
| MDD, Ctrl | <.0001 | .5362 | <.0001 | <.0001 | .0069 | <.0001 |
| HR, Ctrl | <.0001 | .4170 | <.0001 | <.0001 | .0043 | <.0001 |
The cdf of MDD-right distances is significantly smaller than HR-right distances which implies HR-right <ST MDD-right. But K-S test yields significant result for both types of one-sided alternative for MDD-right, Ctrl-right and HR-right, Ctrl-right and MDD-left and HR-left pairs (see Table 4 and Figure 5). This implies, for example, the cdfs of MDD-right and Ctrl-right distances are different, but the differences between the cdfs of the groups change over the distance values; that is, for small distances, the order of cdfs for right distances is Ctrl<MDD<HR, which is the order for the proportion of voxels with smaller distances to the total number of voxels. Hence there is no stochastic ordering between them. That is, the proportion of voxels with smaller distances is largest for HR subjects and smallest for Ctrl subjects. For large distances the order of cdfs for right distances is HR<MDD<Ctrl, which can be interpreted similarly. This result indicates the cortical thinning for HR and MDD subjects compared to Ctrl subjects in the right VMPFC.
4 The Influence of Assumption Violations: A Monte Carlo Analysis
In this section, we investigate the influence of the assumption violations due to the spatial correlation and non-normality inherent in the LCDM distances on the tests. The most crucial step in a Monte Carlo simulation is being able to generate distances resembling those of LCDM distances of GM in VMPFCs; i.e., simulating the true randomness in LCDM distances.
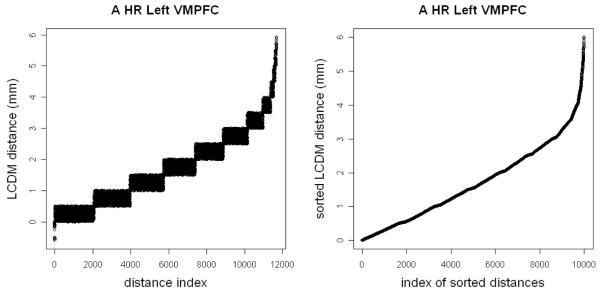
For illustrative purposes, we choose the left VMPFC of HR subject 1. Recall that the LCDM distances for left VMPFC of HR subject 1 are denoted as . We rearrange the distances, , so that first stack of distances is in the interval I0 := [−1,0.5] mm , the second stack of distances is in I1 := (0.5,1.0] mm , the third stack of distances is in I2 := (1.0,1.5] mm , and so on (until the last stack of distances is in I11 := (5.5,6.0] mm). Let νi be the number of distances that fall in Ii i.e., , for i = 0,1,2,…,11 . Hence ν = (ν0,ν1,…,ν11) = (2059, 1898, 1764, 1670, 1492, 1268, 814, 417, 142, 81, 61, 16). Then we merge these stacks into one group, (by appending to for i = 1,2,…,10). See Figure 2, where the left graph is for the stacked distances and the right graph is for distances sorted in ascending order.
Figure 2.
Plots of the LCDM distances for the left VMPFC of HR subject 1. The left plot is for the distances stacked for intervals of size 0.5 mm and the right plot is for the sorted distances.
A possible Monte Carlo simulation for these distances can be performed as follows. We independently generate n numbers in {0,1,2,…,11} proportional to the above frequencies, νi, with replacement, i.e., with the discrete probability mass function PN (Nj = i) = νi/11659 for i = 1,2,…,11 and j = 1,2,…,n. So, PN (Nj = i) = νp,i where
| (5) |
Let ni be the frequency of i among the n generated numbers from {0,1,2,…,11} with distribution PN, for i = 1,2,…,11. Hence . Then we generate as many U(0,1) numbers for each i ∈{0,1,2,…,11} as i occurs in the generated sample of 1000 numbers and add these uniform numbers to i . That is, we generate for k = 1,2,…,ni for each i . Then we divide each distance by 2 to make the range of generated distances [0,6.0] mm which is the range of , so the desired distance values are dik = (i+Uik )/2 . Hence the set of simulated distances is
| (6) |
A sample of the distances generated in this fashion is plotted in Figure 3 where the left plot is for the distances as they are generated at each bin (stack) of size 0.5 mm, the right plot is for the distances sorted in ascending order. Comparing Figure 2 and Figure 3, we observe that the Monte Carlo scheme described above generates distances that resemble LCDM distances for left VMPFC of HR subject 1. Therefore the distances generated in this fashion together with modification of some parameters such as νp,i would resemble the distances of VMPFCs from real subjects. That is, when such parameters are modified in the Monte Carlo scheme described above, the differences in the LCDM distances could simulate the morphometric differences between real subjects.
Figure 3.
Plots of the data values generated by Monte Carlo simulation to resemble LCDM distances. The left plot is for the distances stacked for intervals of size 0.5 and the right plot is for the sorted distances.
4.1 Simulation of Distances that Resemble LCDM Distances
In our Monte Carlo study, we generate three samples , , and with sizes nx , ny , and nz , respectively, and set nx = ny = nz =10000. Each sample is generated similar to the procedure described above. For example, sample is generated as follows: First we generate
| (7) |
where with is the ith entry in and is also the ith value after the entries |νi-ηx | are sorted in descending order for i = 0,1,2,…,11 and . Let be the frequency of i among the nx generated numbers from PX . Then we generate for for each i . Hence the set of simulated distances for set is
| (8) |
Samples and are generated similarly with parameter subscripts in (7) and (8) are modified accordingly.
4.2 Empirical Size Estimates for the Multi-Sample Case
For the null hypothesis of multi-sample case which states the equality of the distributions of LCDM distances, we generate three samples , , and with the below parameters:
| (9) |
Notice that each sample is generated so as to resemble those of the left VMPFC of HR subject 1 up to scale. This is done without loss of generality, since any other VMPFC can either be obtained by a rescaling of the generated distances or by modifying the parameters. So for example, for sample , PX(Xj = i) = νp,i with νp,i being the ith entry in vp in Equation (5) and the set of simulated distances for set is as in Equation (8) with rx = 1.0 and ηx = 0.
We repeat this sample generation procedure Nmc = 10000 times. We count the number of times the null hypothesis is rejected at α = 0.05 level for K-W test of distributional equality and ANOVA F-tests (with and without HOV) of equality of mean distances. The ratio of the number of significant results by each test to Nmc yields the estimated significance levels under Ho. The estimated significance levels for various values of nx , ny , and nz are provided in Table 5, where is the empirical size estimate for K-W test, is for ANOVA F-test with HOV, and is for ANOVA F-test without HOV. Furthermore, is the proportion of agreement between K-W and ANOVA F-test with HOV, i.e., the number of times out of 10000 Monte Carlo replicates both KW and ANOVA F-test with HOV reject the null hypothesis. Similarly, is the proportion of agreement between K-W and ANOVA F-test without HOV, and is the proportion of agreement between ANOVA F-test with HOV and ANOVA F-test without HOV. Using the asymptotic normality of the proportions, we test the equality of the empirical size estimates with 0.05, and compare the empirical sizes pairwise. We observe that the K-W test is at the desired significance level, while ANOVA F-tests with and without HOV are at the desired level or slightly conservative. Notice also that under Ho, the tests tend to be more conservative as the sample sizes increase. Hence, if the distances are not that different; i.e., the frequency of distances for each bin and the distances for each bin are identically distributed for each group, the inherent spatial correlation does not seem to influence the significance levels. Moreover, we observe that for LCDM distances K-W and ANOVA with HOV tests have significantly different rejection (hence acceptance) regions, because the proportion of agreement for these tests, is significantly smaller than the minimum of and , . Similarly, K-W and ANOVA without HOV tests have significantly different rejection (hence acceptance) regions because, the proportion of agreement for these tests, is significantly smaller than . However, ANOVA with and without HOV tests have about the same rejection (hence acceptance) regions because, the proportion of agreement for these tests, is not significantly different from . This mainly results from the fact that K-W and ANOVA with HOV tests test different hypotheses, and so do the K-W and ANOVA without HOV tests. But, ANOVA with and without HOV tests basically test the same hypotheses.
Table 5.
Estimated significance levels and proportions of agreement between the tests based on Monte Carlo simulations of distances with three groups, , , and with sizes nx , ny , and nz , respectively, with Nmc =10000 Monte Carlo replicates. is the empirical size estimate for K-W test, , are for ANOVA F-tests with and without HOV, respectively; , , and are the values of proportion of agreement between the indicated tests in the subscripts. The empirical sizes in the same row with the same superscript are not significantly different from each other. (>(<) Empirical size is significantly larger (smaller) than 0.05; i.e. method is liberal (conservative); (ℓ (≈) The proportion of agreement (not) significantly less than the minimum of the empirical sizes. )
| Empirical size | Prop. of agreement | |||||
|---|---|---|---|---|---|---|
| (nx,ny,nz) | ||||||
| (1000,1000,1000) | .0511 a |
.0508a | .0506a | .0417ℓ | .0419ℓ | .0499≈ |
| (5000,5000,10000) | .0495 a |
.0498a | .0497a | .0386ℓ | .0386ℓ | .0491≈ |
| (5000,7500,10000) | .0480 a |
.0451a, < |
.0449a, < |
.0368ℓ | .0369ℓ | .0446≈ |
| (10000,10000,10000) | .0483 a |
.0483a | .0480a | .0392ℓ | .0392ℓ | .0477≈ |
4.3 Empirical Power Estimates for Multi-Sample Case
For the alternative hypothesis, we generate sample as in the null case, so is as in Equation (8). We consider various ry and ηy values for sample and various rz and ηz values for sample . The five alternative cases we consider are
| (10) |
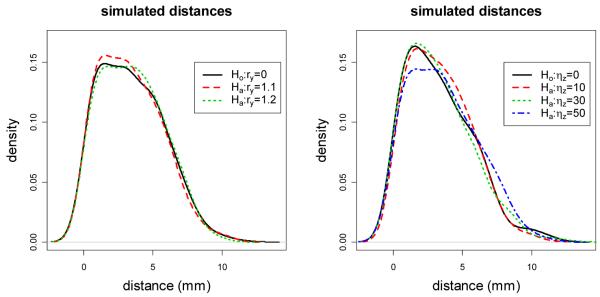
See Figure 4 for the kernel density estimates of sample distances under the null case and various alternatives.
Figure 4.
Plots of the kernel density estimates of the Monte Carlo simulated LCDM distances under the null case and alternatives with ηz = 0 and ry ∈ {1.1,1.2} (left); null case and alternatives with ry = 1.0 and ηz ∈ {10,30,50} (right). For the parameters ry and ηz, see Section 4.
We repeat the sample generation Nmc = 10000 times under each alternative case. We count the number of times the null hypothesis is rejected at α = 0.05 for K-W test of distributional equality, and ANOVA F-tests (with and without HOV) of equality of mean distances, and find the ratio of number of significant results by each test to Nmc . Thus we obtain the empirical power estimates under Ha which are provided in Table 6, where is the empirical power estimate for K-W test, is for ANOVA F-test with HOV, and is for ANOVA F-test without HOV. Using the asymptotic normality of the empirical power estimates, we observe that under each of Ha cases with (ry,rz,ηy,ηz)∈{(1.1,1.0,0,0),(1.1,1.2,0,0)} the distributions are different, so the larger the ry and rz from 1.0, the higher the power estimates for K-W and ANOVA F-tests. Furthermore, as the sample size n increases, the power estimates for K-W and ANOVA F-tests also increase. Notice that under these alternatives, the K-W test tends to be more powerful than ANOVA F-tests, since such alternatives influence the ranking (hence the distribution) of the distances, more than the mean of the distances. Furthermore, under these alternatives, it is not the size or scale that is really different; it is the difference in shape that is more emphasized. The size component is distance with respect to the GM/WM surface; i.e., if the GM voxels from the GM/WM surface are at about the same distance, the K-W test is more sensitive to the differences in the distributions of the LCDM distances. We also note that ANOVA F-tests with and without HOV have about the same power estimates.
Table 6.
The power estimates based on Monte Carlo simulation of distances with three groups, , , and with sizes nx , ny , and nz , respectively, with Nmc =10000 Monte Carlo replicates. is the empirical power estimate for K-W test, and are for ANOVA F-tests with and without HOV, respectively. The superscripts of the power estimates in the same row are labeled in increasing order of significance. That is, the power estimates with the same superscript are not significantly different from each other; while power estimate with label a is significantly smaller than the estimate labeled with b , and so on
| (ry,rz)=(1.1,1.0); (ηy,ηz) = (0,0) | |||
|---|---|---|---|
| (nx,ny,nz) | |||
| (1000,1000,1000) | .0778a | .0770a | .0768 a |
| (5000,5000,10000) | .2281a | .2137b | .2114 b |
| (5000,10000,5000) | .2936a | .2731b | .2745 b |
| (5000,10000,7500) | .3244a | .2939b | .2947 b |
| (10000,10000,10000) | .3900a | .3564b | .3559 b |
| (ry,rz)=(1.1,1.2); (ηy,ηz) = (0,0) | |||
| (1000,1000,1000) | .1396a | .1316a b |
.1313b |
| (5000,5000,10000) | .6725a | .6315b | .6317b |
| (10000,5000,5000) | .6651a | .6262b | .6253b |
| (5000,10000,5000) | .5296a | .4828b | .4828b |
| (10000,10000,10000) | .8410a | .8050b | .8050b |
| (ry,rz) = (1.0,1.0); (ηy,ηz)=(10,0) | |||
| (1000,1000,1000) | .0574 b |
.0728a | .0721a |
| (5000,5000,10000) | .0767 b |
.1930a | .1854a |
| (5000,10000,5000) | .0884 b |
.2341a | .2381a |
| (5000,7500,10000) | .0832 b |
.2415a | .2360a |
| (5000,10000,7500) | .0878 b |
.2571a | .2584a |
| (10000,10000,10000) | .1006 b |
.3127a | .3061a |
| (ry,rz) = (1.0,1.0); (ηy,ηz)=(10,30) | |||
| (1000,1000,1000) | .0963 b |
.1519a | .1512a |
| (5000,5000,10000) | .3986 b |
.7436a | .7537a |
| (10000,5000,5000) | .3556 b |
.7175a | .7071a |
| (5000,10000,5000) | .2908 b |
.5826a | .5831a |
| (5000,7500,10000) | .4191 b |
.7578a | .7627a |
| (10000,7500,5000) | .3652 b |
.7229a | .7147a |
| (10000,5000,7500) | .4554 b |
.8260a | .8226a |
| (7500,5000,10000) | .4739 b |
.8331a | .8363a |
| (7500,10000,5000) | .3421 b |
.6743a | .6702a |
| (5000,10000,7500) | .3752 b |
.6938a | .6983a |
| (10000,10000,10000) | .5352 b |
.8842a | .8835a |
Under each of alternative cases with
| (11) |
as ηy and ηz deviate more from 0, the power estimates for K-W and ANOVA F-tests increase. Note that as n increases, the power estimates also increase under these alternative cases. Under these second type of alternatives, ANOVA F-tests tend to be more powerful, since the right skewness (tail) of distances are more emphasized, which in turn implies that the differences in the mean distances are emphasized more. Under these alternatives, both the size or scale and shape are different. If the GM voxels from the GM/WM surface are at different distances, ANOVA F-tests are more sensitive to the differences in LCDM distances. We also note that both ANOVA F-tests (with and without HOV) have about the same power estimates.
4.4 Empirical Size Estimates for the Two-Sample Case
For the null hypothesis for the two-sample case, we generate two samples and each of size nx and ny , respectively. Each sample is generated as described in Section 4.2. We repeat the sample generation Nmc = 10000 times.
We count the number of times the null hypothesis is rejected at α = 0.05 for Lilliefor’s test of normality, Wilcoxon rank sum test of distributional equality, t-test of equality of mean distances, and K-S test of equality of cdfs, and find the ratio of the number of significant results by each test to Nmc , thereby obtain the estimated significance levels. Unlike the multi-sample case, for the two-sample case, except for Lilliefor’s test there are three types of alternative hypotheses possible: two-sided, left, and right-sided alternatives. The estimated significance levels are provided in Table 7, where is the empirical size estimate for Wilcoxon rank sum test, is for t-test, is for K-S test. Furthermore, is the proportion of agreement between Wilcoxon rank sum and t-tests, is the proportion of agreement between Wilcoxon rank sum and K-S tests, and is the proportion of agreement between t-test and K-S test. We omit the Lilliefor’s test, since by construction, our samples are severely non-normal, so normality is rejected for virtually all samples generated. Observe that under Ho, the empirical significance levels are about the desired level for all three types of alternatives, although Wilcoxon tests are slightly liberal, while K-S test is slightly conservative. Hence, if the distances are not that different; i.e., the frequency of distances for each bin and the distances for each bin are identically distributed for each group, the inherent spatial correlation does not influence the significance levels. However, Wilcoxon rank sum, t-test, and K-S methods test different hypotheses, so their acceptance and rejection regions are significantly different for LCDM distances, since the proportion of agreement for each pair is significantly smaller than the minimum of the empirical size estimates for each pair of tests.
Table 7.
Estimated significance levels based on Monte Carlo simulation of distances with two groups and with sizes nx and nz , respectively, with Nmc =10000 Monte Carlo replicates. is the empirical size estimate for Wilcoxon rank sum test, is for t-test, is for K-S test; , , and are the values of proportion of agreement between the indicated tests in the subscripts. The superscript labeling for conservativeness and liberalness of empirical sizes and for proportions of agreement values are as in Table 5 and for ordering of the power estimates for each row is as in Table 6
| Two-sided Tests | ||||||
|---|---|---|---|---|---|---|
| Empirical size | Prop. of agreement | |||||
| (nx,ny) | ||||||
| (1000,1000) | .0517a | .0505a | .0486a | .0403ℓ | .0305ℓ | .0273ℓ |
| (5000,10000) | .0457b, < |
.0463b, < |
.0465 b |
.0356ℓ | .0273ℓ | .0244ℓ |
| (7500,10000) | .0493a | .0463a,< | .0464a | .0385ℓ | .0282ℓ | .0246ℓ |
| (10000, 10000) | .0518a | .0525a | .0501a | .0421ℓ | .0320ℓ | .0281ℓ |
| Left-Sided Tests (i.e., values tend to be smaller than values) | ||||||
| Empirical size | Prop. of agreement | |||||
| (1000,1000) | .0517a | .0527a | .0486a | .0440ℓ | .0329ℓ | .0305ℓ |
| (5000,10000) | .0470a | .0489a | .0492a | .0382ℓ | .0311ℓ | .0282ℓ |
| (7500,10000) | .0490a | .0493a | .0478a | .0399ℓ | .0322ℓ | .0284ℓ |
| (10000, 10000) | .0517a | .0514a | .0494a | .0426ℓ | .0330ℓ | .0301ℓ |
| Right-Sided Tests (i.e., values tend to be larger than values) | ||||||
| Empirical size | Prop. of agreement | |||||
| (1000,1000) | .0521a | .0502a | .0491a | .0409ℓ | .0337ℓ | .0294ℓ |
| (5000,10000) | .0486a | .0502a | .0478a | .0405ℓ | .0308ℓ | .0285ℓ |
| (7500,10000) | .0479a | .0469a | .0495a | .0391ℓ | .0325ℓ | .0287ℓ |
| (10000, 10000) | .0532a | .0517ab | .0469 b |
.0435ℓ | .0354ℓ | .0311ℓ |
4.5 Empirical Power Estimates for the Two-Sample Case
For the alternative hypotheses, we generate samples and as in Section 4.3 also. Note that when ry = 1 and ηy = 0, we obtain the null case. The five alternative cases we consider are (ry,ηy )∈{(1.1,0),(1.2,0),(1.0,10),(1.0,30),(1.0,50)}. We count the number of times the null hypothesis is rejected for Lilliefor’s test of normality, Wilcoxon rank sum test of distributional equality, t-test of equality of mean distances, and K-S test of equality of cdfs, thereby obtain the estimated significance levels as before. The power estimates are provided in Table 8, where is the power estimate for Wilcoxon rank sum test, is for t-test, is for K-S test.
Table 8.
The power estimates based on Monte Carlo simulation of distances with two groups, , and , with sizes nx , and ny, respectively, with Nmc =10000 Monte Carlo replicates. is the power estimate for Wilcoxon rank sum test, is for t-test, is for K-S test. The superscript labeling for ordering of the power estimates in each row is as in Table 6
| Two-Sided | Left-Sided | |||||
|---|---|---|---|---|---|---|
| ry=1.1; ηy=0 | ||||||
| (nx,ny) | ||||||
| (1000,1000) | .1317a | .1264a | .0788 b |
.0742a | .0712a | .0750a |
| (5000,10000) | .2723 b |
.2520c | .3734 | .3816 b |
.3600c | .5122a |
| (10000,5000) | .2720 b |
.2507c | .3753 | .3838 b |
.3572c | .5157a |
| (7500,10000) | .3242 b |
.3046c | .4731 | .4425 b |
.4178c | .6139a |
| (10000,7500) | .3305 b |
.3100c | .4850 | .4455 b |
.4204c | .6253a |
| (10000,10000) | .3662 b |
.3362c | .5504 | .4924 b |
.4588c | .6861a |
| ry=1.2; ηy = 0 | ||||||
| (1000,1000) | .2635a | .2533a | .1838 b |
.1695 b |
.1630 b |
.1813a |
| (5000,10000) | .7606 b |
.7331c | .9401a | .8463 b |
.8250c | .9755a |
| (10000,5000) | .7588 b |
.7269c | .9421a | .8437 b |
.8178c | .9765a |
| (7500,10000) | .8514 b |
.8282c | .9839a | .9121 b |
.8950c | .9945a |
| (10000,7500) | .8561 b |
.8300c | .9845a | .9133a | .8969 b |
.8882c |
| (10000,10000) | .8976 b |
.8750c | .9935a | .9468 b |
.9312c | .9982a |
| ry=1.0; ηy =10 | ||||||
| (1000,1000) | .0772c | .1173a | .0514 d |
.0506c | .0677 b |
.0477c |
| (5000,10000) | .0871c | .2222 b |
.0673 d |
.1361c | .3297 b |
.1089d |
| (10000,5000) | .0841c | .2186 b |
.0670 d |
.1390c | .3232 b |
.1076d |
| (7500,10000) | .0951c | .2638 b |
.0737 d |
.1497c | .3786 b |
.1159d |
| (10000,7500) | .0995c | .2630 b |
.0748 d |
.1560c | .3725 b |
.1161d |
| (10000,10000) | .1018c | .2978 b |
.0743 d |
.1628c | .4132 b |
.1200d |
| ry=1.0; ηy = 30 | ||||||
| (1000,1000) | .1760 b |
.2887a | .0878c | .1028c | .1885 d |
.0793d |
| (5000,10000) | .4677 d |
.8254 b |
.7080c | .5927c | .8881 b |
.8911b |
| (10000,5000) | .4668 d |
.8094 b |
.6901c | .5918 d |
.8807 b |
.8659c |
| (7500,10000) | .5578 d |
.8987c | .9078 b |
.6773 d |
.9435c | .9792b |
| (10000,7500) | .5509c | .8976 b |
.8983 b |
.6750 d |
.9438c | .9713b |
| (10000,10000) | .6188 d |
.9369c | .9691 b |
.7339 d |
.9679c | .9942b |
| ry=1.0; ηy = 50 | ||||||
| (1000,1000) | .3361c | .4865a | .2041 d |
.2266c | .3521 b |
.2048d |
| (5000,10000) | .8876c | .9842 b |
.9980 b |
.9363c | .9936 d |
.9998a |
| (10000,5000) | .8830c | .9844 b |
.9980a | .9325 d |
.9931c | 1.000a |
| (7500,10000) | .9478c | .9964 b |
1.000a | .9932c | .9986 b |
1.000a |
| (10000,7500) | .9473c | .9961 b |
1.000a | .9741c | .9984 b |
1.000a |
| (10000,10000) | .9716c | .9984 b |
1.000a | .9847c | .9995 b |
1.000a |
Under the alternative cases with (ry,ηy)∈{(1.1, 0),(1.2,0)}, we see that the distributions start to differ. As ry deviates further away from 1.0, then the power estimates for Wilcoxon rank sum, t-test, and K-S tests increase. Furthermore, as the sample size n increases, the power estimates for Wilcoxon test, t-test, and K-S test also increase. Observe that as in the multi-sample case, under these alternatives, Wilcoxon test is more powerful than t-test, since the ranking of the distances are affected more than the mean distances under these alternatives. But K-S test has the highest power estimates for sample sizes larger than 1000. Thus, for differences in shape rather than the distance from the GM/WM surface, K-S test and Wilcoxon rank sum test are more sensitive (i.e., powerful) than t-test. Furthermore, as the sample sizes increase, the left-sided tests become more powerful than their two-sided counterparts. Notice that we omit the power estimates for the right-sided alternatives, since by construction (i.e., due to our parameter choices in our simulations) values tend to be smaller than values for these alternatives; hence the tests virtually have no power for the right-sided alternatives.
Under the Ha cases with (ry,ηy)∈{(1.0,10),(1.0,30),(1.0,50)}, as ηy deviates further away from 0, the power estimates for Wilcoxon rank sum, t-test, and K-S tests increase. Note that as n increases, the power estimates also increase under each alternative case. Under these alternatives, t-test is more powerful than Wilcoxon test, since mean distances are more affected than the rankings under such alternatives. However, K-S test has higher power estimates for larger deviations from the null case. These alternatives imply that the distances of the GM voxels are at different scales, t-test has the best performance for small differences, while for large differences, K-S has the best performance. Furthermore, as the sample sizes increase, the left-sided tests become more powerful than their two-sided counterparts. Again, we omit the power estimates for the right-sided alternatives, because, by construction, values tend to be smaller than values for these alternatives.
We do not report the power estimates for Lilliefor’s test of normality, since by construction our data is severely non-normal, and we get power estimates of 1.000 under both null and alternative cases.
5 Discussion and Conclusions
Pooled LCDM distances, when used as a single variable, provide a method to analyze heterogeneous forms of morphometric differences. When the LCDM distances of the subjects in the same diagnostic group are pooled, common morphometric traits of the ROI for that group are accentuated. Conversely, the morphometric traits not common for all the subjects in a group but specific to a particular subject are downplayed. The most common morphometric traits in a relevant ROI in a particular group may be associated with the diagnosis of the group and pooled LCDM distances carry on the most common characteristics, so they have the potential as demonstrated here to be very sensitive in detecting the diagnosis-specific traits of the ROI. As a result, they can indicate changes in the ROI highly associated with disease (major depression in the VMPFC in this article) or associated with being at genetic risk for the development of a specific condition. When pooled distances yield significant results, it implies that ROI significantly differ in morphometry (shape or size). However, it does not indicate the specific location within a ROI where such differences occur which might be important for understanding the underlying neurobiology. This may require the use of censoring which is the topic of another paper.
We use Kruskal-Wallis (K-W) and ANOVA F-tests (with or without HOV) for multi-group comparisons, Wilcoxon rank sum, Kolmogorov-Smirnov (K-S), and t-tests for two-group comparisons (the first two of these tests used to test distributional differences and the third is used to test mean differences due to a location parameter). But these tests require within sample independence which is violated due to the spatial correlation between LCDM distances of nearby voxels. Furthermore, parametric tests require normality of the samples also, which is again violated due to the heavy right skewness of the LCDM distances. However, our Monte Carlo analysis indicates that the influence of these violations is mild or negligible. Furthermore, the tests are more sensitive against different alternatives. In particular, K-W and Wilcoxon tests (i.e., the nonparametric tests) are more sensitive to distributional differences in a ROI with similar laminar thickness, while ANOVA F-tests and t-test (i.e., parametric tests) are more sensitive against the differences in the means, that is, differences in average GM thickness (i.e., laminar thickness values). On the other hand, K-S test is more sensitive to the largest difference in the cdfs of the LCDM distances.
Although the focus of this paper is the description of new morphologic image processing methods, as an illustrative example, we use GM tissue in the Ventral Medial Prefrontal Cortex (VMPFC) as the ROI for three groups of subjects; namely, subjects with major depressive disorder (MDD), subjects at high risk (HR) for MDD, and unrelated healthy control subjects (Ctrl). Based on previous results from other groups with older adult populations, we expected to find cortical differences associated with affective disorders in this region, however the nature of the changes or if they are present in younger populations has not been well characterized. Our study comprises of adolescent and young adult (MDD, HR) and (Ctrl, Ctrl) co-twin pairs. We found that gray matter distances in left and right VMPFC tend to decrease associated with MDD or being at HR for MDD, which is a characteristic that would be associated with cortical thinning. We thus observe a significant reduction in laminar thickness of VMPFC and perhaps shrinkage in MDD when compared to Ctrl subjects. However the same trend is also seen in the HR subjects, who are typical healthy individuals except for their genetic relation to the depressed cotwins. Thus this study does not support that all of the changes in morphometry of VMPFCs is related directly to major depression. It could be possible that VMPFC tend to shrink due to depression, but as similar shrinkage is seen in HR subjects, it could also be the case that specific genetic factors might predispose to this morphometric difference in VMPFC which in turn leads to vulnerability for developing depression in young individuals. Furthermore, in the pooled LCDM distance analysis, we find that the central values (i.e., means and medians) of the pooled distances in left VMPFCs of MDD and HR subjects are not significantly different, but the orderings of the central values of LCDM distances are MDD < Ctrl and HR < Ctrl; in right VMPFCs the ordering is as HR < MDD < Ctrl. Our findings here support that there are significant lateralization differences in the contribution of this region to affective disorders; similar asymmetry or lateralization findings have been previously reported in functional and structural studies [13, 18] and functional lateralization in this region has also been reported in animal models [9]. The cdf comparisons indicate that it is more likely for left VMPFCs of MDD or HR subjects to be thinner than those of Ctrl subjects which confirm the above findings about cortical thinning. However no such stochastic ordering occurs for the right VMPFCs, which only indicates the cdf orderings depend on the distance values in the right VMPFCs.
We demonstrate that pooled LCDM distances may provide a useful tool in detecting morphometric differences associated with specific disorders which affect the cortex. There is increasing recognition that different cortical features such as surface area or thickness may provide clues to different underlying pathology [6]. For instance increased GM distribution at shorter distances may represent increased surface area or increased curvature which could be further investigated via different methods. Attaining similar maximum long distances with a lower gray matter concentration at nearby long distances could indicate achievement of expected cortical thickness with loss of thickness in certain subregions within the ROI. Additional characterization of cortex may lead to improved sensitivity to detect differences associated with specific disorders. For example, the thickness at each point on the surface can be measured, which means mapping the surfaces to a template and then doing the statistics at each point on the surface. For this purpose, the first step is to apply LLCDM and then apply LDDMM-Surface (see [20, 21]). We also note that the LCDM based methodology used in this article can be applied to many different cortical regions.
Acknowledgements
We would like to thank the editors and anonymous referees whose constructive remarks and suggestions greatly improved the presentation and flow of this article. Most of the Monte Carlo simulations presented in this article were executed at Koç University High Performance Computing Laboratory. Research supported by R01-MH62626-01 and P41-RR15241.
References
- 1.Barker AR, Priebe CE, Miller MI, Hosakere M, Lee N, Ratnanather JT, Wang L, Gado M, Morris JC, Csernansky JC. Statistical Testing on Labeled Cortical Distance Maps to Identify Dementia Progression; Joint Statistical Meeting, Section on Nonparametric Statistics; San Francisco. 2003; American Statistical Association. [Google Scholar]
- 2.Botteron KN, Raichle ME, Drevets WC, Heath AC, Todd RD. Volumetric reduction in the left subgenual prefrontal cortex in early onset depression. Biological Psychiatry. 2002;51(4):342–344. doi: 10.1016/s0006-3223(01)01280-x. [DOI] [PubMed] [Google Scholar]
- 3.Bridge H, Clare S, Jenkinson M, Jezzard P, Parker AJ, Matthews PM. Independent anatomical and functional measures of the V1/V2 boundary in human visual cortex. Journal of Vision. 2005;5(2):93–102. doi: 10.1167/5.2.1. [DOI] [PubMed] [Google Scholar]
- 4.Ceyhan E, Hosakere M, Nishino T, Alexopoulos J, Todd RD, Botteron KN, Miller MI, Ratnanather JT. Technical Report KU-EC-08-2: The Use of Labeled Cortical Distance Maps for Quantization and Analysis of Anatomical Morphometry of Brain Tissues. Koç University; Istanbul: 2008. available as arXiv:0805.3835v1 [stat.CO] at http://arxiv.org/ [Google Scholar]
- 5.Ceyhan E, Hosakere M, Nishino T, Babb C, Todd RD, Ratnanather JT, Botteron KN. Statistical Analysis of Morphometric Measures Based on Labeled Cortical Distance Maps; Fifth International Symposium on Image and Signal Processing and Analysis (ISPA 2007); Istanbul, Turkey. 2007. [Google Scholar]
- 6.Chenn A, Walsh CA. Increased Neuronal Production, Enlarged Forebrains and Cytoarchitectural Distortions in Beta-Catenin Overexpressing Transgenic Mice. Cerebral Cortex. 2003;13:599–606. doi: 10.1093/cercor/13.6.599. [DOI] [PubMed] [Google Scholar]
- 7.Chung MK, Robbins SM, Dalton KM, Davidson RJ, Alexander AL, Evans AC. Cortical thickness analysis in autism with heat kernel smoothing. NeuroImage. 2005;25(4):1256–1265. doi: 10.1016/j.neuroimage.2004.12.052. [DOI] [PubMed] [Google Scholar]
- 8.Conover W. Practical Nonparametric Statistics. 3rd ed. John Wiley & Sons; New York: 1999. [Google Scholar]
- 9.Czéh B, Müller-Keuker JI, Rygula R, Abumaria N, Hiemke C, Domenici E, Fuchs E. Chronic social stress inhibits cell proliferation in the adult medial prefrontal cortex: hemispheric asymmetry and reversal by fluoxetine treatment. Neuropsychopharmacology. 2007;32(7):1490–503. doi: 10.1038/sj.npp.1301275. [DOI] [PubMed] [Google Scholar]
- 10.Drevets WC, Price JL, Simpson JR, Todd RD, Reich T, Vannier M, Raichle ME. Subgenual prefrontal cortex abnormalities in mood disorders. Nature. 1997;386:824–827. doi: 10.1038/386824a0. [DOI] [PubMed] [Google Scholar]
- 11.Elkis H, Friedman L, Buckley PF, Lee HS, Lys C, Kaufman B, Meltzer HY. Increased prefrontal sulcal prominence in relatively young patients with unipolar major depression. Psychiatry Research: Neuroimaging. 1996;67(2):123–134. doi: 10.1016/0925-4927(96)02744-8. [DOI] [PubMed] [Google Scholar]
- 12.Joshi M, Cui J, Doolittle K, Joshi S, Van Essen D, Wang L, Miller MI. Brain segmentation and the generation of cortical surfaces. NeuroImage. 1999;9(5):461–476. doi: 10.1006/nimg.1999.0428. [DOI] [PubMed] [Google Scholar]
- 13.Killgore WD, Gruber SA, Yurgelun-Todd DA. Depressed mood and lateralized prefrontal activity during a Stroop task in adolescent children. Neurosci Lett. 2007;416(1):43–8. doi: 10.1016/j.neulet.2007.01.081. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Makris N, Biederman J, Valera EM, Bush G, Kaiser J, Kennedy DN, Caviness VS, Faraone SV, Seidman LJ. Cortical Thinning of the Attention and Executive Function Networks in Adults with Attention-Deficit/Hyperactivity Disorder. Cerebral Cortex. 2006 doi: 10.1093/cercor/bhl047. [DOI] [PubMed] [Google Scholar]
- 15.Martinussen M, Fischl B, Larsson HB, Skranes J, Kulseng S, Vangberg TR, Vik T, Brubakk AM, Haraldseth O, Dale AM. Cerebral cortex thickness in 15-year-old adolescents with low birth weight measured by an automated MRI-based method. Brain. 2005;128(Pt 11):2588–2596. doi: 10.1093/brain/awh610. [DOI] [PubMed] [Google Scholar]
- 16.Miller MI, Hosakere M, Barker AR, Priebe CE, Lee N, Ratnanather JT, Wang L, Gado M, Morris JC, Csernansky JG. Labeled cortical mantle distance maps of the cingulate quantify differences between dementia of the Alzheimer type and healthy aging. Proceedings of the National Academy of Sciences of the United States of America. 2003;100(25):15172–15177. doi: 10.1073/pnas.2136624100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Miller MI, Massie AB, Ratnanather JT, Botteron KN, Csernansky JG. Bayesian construction of geometrically based cortical thickness metrics. NeuroImage. 2000;12(6):676–687. doi: 10.1006/nimg.2000.0666. [DOI] [PubMed] [Google Scholar]
- 18.Phillips ML, Ladouceur CD, Drevets WC. A neural model of voluntary and automatic emotion regulation: implications for understanding the pathophysiology and neurodevelopment of bipolar disorder. Mol Psychiatry. 2007 doi: 10.1038/mp.2008.65. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Preul C, Lohmann G, Hund-Georgiadis M, Guthke T, von Cramon DY. Morphometry demonstrates loss of cortical thickness in cerebral microangiopathy. Journal of Neurology. 2005;252(4):441–447. doi: 10.1007/s00415-005-0671-9. [DOI] [PubMed] [Google Scholar]
- 20.Qiu A, Vaillant M, Barta P, Ratnanather JT, Miller MI. Region-of-interest-based analysis with application of cortical thickness variation of left planum temporale in schizophrenia and psychotic bipolar disorder. Human Brain Mapping. 2008;29(8):973–985. doi: 10.1002/hbm.20444. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Qiu A, Younes L, Wang L, Ratnanather JT, Gillepsie SK, Kaplan G, Csernansky J, Miller MI. Combining anatomical manifold information via diffeomorphic metric mappings for studying cortical thinning of the cingulate gyrus in schizophrenia. Neuroimage. 2007;37(3):821–833. doi: 10.1016/j.neuroimage.2007.05.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Ratnanather JT, Barta PE, Honeycutt NA, Lee N, Morris HM, Dziorny AC, Hurdal MK, Pearlson GD, Miller MI. Dynamic programming generation of boundaries of local coordinatized submanifolds in the neocortex: application to the planum temporale. NeuroImage. 2003;20(1):359–77. doi: 10.1016/s1053-8119(03)00238-6. [DOI] [PubMed] [Google Scholar]
- 23.Ratnanather JT, Botteron KN, Nishino T, Massie AB, Lal RM, Patel SG, Peddi S, Todd RD, Miller MI. Validating cortical surface analysis of medial prefrontal cortex. NeuroImage. 2001;14(5):1058–1069. doi: 10.1006/nimg.2001.0906. [DOI] [PubMed] [Google Scholar]
- 24.Ratnanather JT, Wang L, Nebel MB, Hosakere M, Han X, Csernansky JG, Miller MI. Validation of semiautomated methods for quantifying cingulate cortical metrics in schizophrenia. Psychiatry Research: Neuroimaging. 2004;132(1):53–68. doi: 10.1016/j.pscychresns.2004.07.003. [DOI] [PubMed] [Google Scholar]
- 25.Wang L, Hosakere M, Trein JC, Miller A, Ratnanather JT, Barch DM, Thompson PA, Qiu A, Gado MH, Miller MI, Csernansky JG. Abnormalities of cingulate gyrus neuroanatomy in schizophrenia. Schizophrenia Research. 2007;93(1-3):66–78. doi: 10.1016/j.schres.2007.02.021. [DOI] [PMC free article] [PubMed] [Google Scholar]