Abstract
Noninvasive brain–computer interfaces (BCI) translate subject's electroencephalogram (EEG) features into device commands. Large feature sets should be down-selected for efficient feature translation. This work proposes two different feature down-selection algorithms for BCI: (a) a sequential forward selection; and (b) an across-group variance. Power rar ratios (PRs) were extracted from the EEG data for movement imagery discrimination. Event-related potentials (ERPs) were employed in the discrimination of cue-evoked responses. While center-out arrows, commonly used in calibration sessions, cued the subjects in the first experiment (for both PR and ERP analyses), less stimulating arrows that were centered in the visual field were employed in the second experiment (for ERP analysis). The proposed algorithms outperformed other three popular feature selection algorithms in movement imagery discrimination. In the first experiment, both algorithms achieved classification errors as low as 12.5% reducing the feature set dimensionality by more than 90%. The classification accuracy of ERPs dropped in the second experiment since centered cues reduced the amplitude of cue-evoked ERPs. The two proposed algorithms effectively reduced feature dimensionality while increasing movement imagery discrimination and detected cue-evoked ERPs that reflect subject attention.
Keywords: Brain–computer interface, EEG, Feature selection, Movement imagery, Event-related potentials
1 Introduction
Current brain–computer interfaces (BCI) determine the intent of the users from a variety of electroencephalographic features [32]. BCIs enable the physically disabled as a consequence of neuromuscular disorders, amyotrophic lateral sclerosis, brainstem stroke or spinal cord injuries to control a device with their brain signals [32]. Noninvasive BCI applications commonly use scalp electroencephalogram (EEG) for laboratory and clinical applications. BCI systems usually adopt one of three operation types: in operant conditioning, the subject is extensively trained to control his own rhythms [33]; in pattern recognition, a classification algorithm discriminates mental task performance by identifying the subject-specific EEG patterns corresponding to each mental task [26]; and in event-related potential (ERP) detection, learning algorithms are employed to detect stimulus-evoked responses in a single-trial basis [13, 21]. Particularly when the latter two BCI approaches are adopted, as increasing number of features are used to train the classifier, the risk of over-fitting to the data increases. The effects of a low ratio of the number of samples to the number of features have been extensively discussed as the ‘‘curse of dimensionality” [7]. Since long training experiments are not practical, a dimensionality reduction technique should be employed to find a feature subset that minimizes the cross-validation error of mental task discrimination.
Two dimensionality reduction methodologies have been adopted in BCI research. In one, studies make use of common-spatial patterns (CSPs) [22, 29], principal component analysis (PCA) [16, 25], and independent component analysis (ICA) [17], among others, that transform the original feature space into lower dimensional spaces. An alternative methodology is feature down-selection which produces a subset of the original features that are most relevant to discriminate subject performance. The greatest advantage of the latter methodology is the effective reduction of BCI computational complexity. Among the methods proposed in previous studies to down-select feature sets are wrapper or filter methods based on dependence on a learning technique [34]. Wrapper methods typically use the predictive accuracy or other performance measures of a pre-selected classifier to evaluate a feature subset. Some exemplars are recursive feature elimination [20] and other sequential selection algorithms [8, 19]. The filter methods separate feature selection from classifier training and produce feature subsets independent of the classifier. The relief algorithm [24] and PCA [2] are often used as filter methods. Genetic algorithms (GAs) are also popular in BCI research [9].
This work proposes two different algorithms to down-select features: (a) a wrapper-type sequential forward selection (SFS) algorithm that adds features to the subset sequentially for task discrimination and (b) a filter type across-group variance (AGV) algorithm, based on a formulation of PCA that accommodates the group structure of the data set. Two different EEG feature types were used: power ratios (PRs) and event-related potentials (ERPs). While PR features were extracted for movement imagery discrimination, the ERP features were extracted in order to detect cue-evoked potentials [13, 21, 30]. The developed algorithms were applied to the data of five subjects with no previous BCI experience. The SFS and AGV algorithms are intended to improve feature selection by maximizing the classification accuracy of the learning algorithm and minimizing both the number of EEG channels selected and the computation time. The performances of the proposed algorithms in movement imagery discrimination were evaluated in comparison to three other feature selection algorithms in common use: recursive feature elimination (RFE) [20], genetic algorithm (GA) [29], and relief [24].
The selection of ERPs intends to determine the optimal EEG channels to detect subject attention in two different experimental conditions: in Experiment 1, the subject was stimulated with center-out asymmetric arrows that are typically used for BCI calibration [3, 12, 26]; in Experiment 2, the subject was stimulated with symmetric arrows that were balanced in the subject visual field.
2 Methods
Five healthy human subjects, 25–32 years old, four males and one female, none of them under any medication, consented to participate in this study. The experiments were conducted under Institutional Review Board (IRB) approval at Penn State University.
2.1 Experimental paradigm
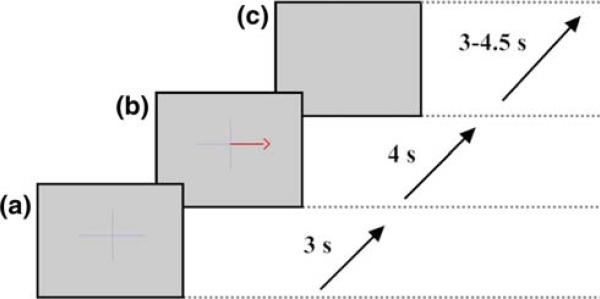
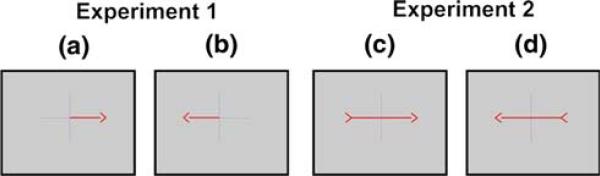
As depicted in Fig. 1, each trial started with the presentation of a cross centered on the screen, informing the subject to be prepared. Three-seconds later, a cue was presented on top of the cross. An arrow that was unbalanced (Experiment 1—Fig. 2a and b) or balanced (Experiment 2—Fig. 2c and d) in the visual field pointed to either left or right on a computer screen to cue the subject on the left or right hand movement imagery tasks. The subject was instructed to perform the movement imagery during a 4-s period starting at the cue presentation. Then, both the cross and the arrow were removed from the screen indicating the end of the trial. The intertrial period was randomly jittered to be between 3 and 4.5 s long. Each experiment had 2 runs of 40 trials each.
Fig. 1.
Paradigm implemented in Experiment 1 for left versus right hand movement imagery tasks: a warning stimulus for a coming cue; b right hand movement imagery cue; and c random intertrial period
Fig. 2.
Screen frames cueing the subject about the movement imagery tasks to perform. In (a) and (b), asymmetric cues were employed in the first EEG experiment while in (c) and (d) the symmetric cues were employed in the second EEG experiment (frames from left to right: right hand and left hand)
2.2 Electrode settings
Data were acquired from 19 electrodes according to an extension of the standard 10–20 system (i.e., Fp1, Fp2, F7, F3, Fz, F4, F8, T7, C3, Cz, C4, T8, P7, P3, Pz, P4, P8, O1, and O2). All electrodes were referenced to linked earlobes.
Data were digitized at 256 Hz and passed through a fourth order 0.5–60 Hz band-pass filter. Each channel's raw EEG signal was epoched from the cue time point to 4 s after the cue. The presence of artifacts in the epochs was automatically detected through the commercial EEG software Brain Vision Analyzer, Brain Products GmbH, that checks for maximum allowed absolute value (50 μV) at any time point, or maximum allowed absolute potential difference (20 μV) between two consecutive time points. The epochs contaminated with artifacts (e.g., eye blinks, muscle artifacts) were excluded from further analyses. The EEG features were extracted from 50 to 75 epochs out of 80 that were not contaminated with artifacts.
Data were re-referenced in order to improve the spatial resolution for coherence estimates. Because of the limitation of each re-referencing method [27], the original data were referenced to a common-average and to a Laplacian filter , according to Eqs. 1 and 2. Si contains the four electrodes surrounding the central electrode . The Laplacian filter calculates a weight gij for each peripheral electrode which depends on the distances dij between the j peripheral electrodes in Si and the central electrode i, according to Eq. 2.
| (1) |
| (2) |
2.3 Power ratios
Alpha (8–14 Hz) and beta (16–24 Hz) EEG frequency bands include rhythms that are reactive to movement imagery [32]. Alpha is an idling rhythm which is also termed “rolandic mu rhythm” when generated in a motor-related cortex area. Alpha amplitude decreases during the execution of, as well as with imagined, limb movement at motor-related cortical locations. Beta rhythm generally increases in amplitude at limb movement initiation and termination at motor-related cortical locations [32].
The epochs used to extract the EEG power ratios include the data from the whole imagery time period (0–4 s from the time the cue is presented). Five narrow frequency bands were defined: 8–12 Hz (low alpha band); 10–14 Hz (high alpha band); 16–20 Hz (low beta band); 18–22 Hz (mid-beta band); and 20–24 Hz (high beta band). The power in the frequency broad band 0.5–30 Hz was used to normalize the power contained in the narrow bands. The power spectral density (PSD) was calculated through a periodo-gram to provide high-frequency resolution (no significant differences were found between periodogram and Welch methods). Each band power was computed as the sum of all PSD components (in V2/Hz) in the corresponding frequency range. The PR feature matrices had 95 features (5 PR features × 19 electrodes).
2.4 Event-related potentials
Event-related potentials are slow, nonoscillatory EEG potential shifts in response to certain events (e.g., visual or auditory stimuli) [23]. The ERP in response to auditory or visual stimuli can be modulated in amplitude and latency by stimulus parameters such as intensity [23], spatial distribution [31], familiarity [11] and EEG phase [18], as well as attention [21].
Following PR extraction, the raw epoch 0–1 s (post-stimulus) was low-pass filtered at 4 Hz with an eighth-order Chebyshev type I filter and used for ERP extraction. This epoch demonstrated the best task discrimination in previous work [5]. The filtered 256 point time series was down-sampled to 10 points per second. The first eight time points of the down sampled time series represent the features to be extracted from each EEG channel. A feature matrix with 152 features (8 ERP features × 19 electrodes) was generated.
3 Feature subset selection methods
The original feature matrix Y has samples (n) in rows and features (p) in columns. Considering that just a few q features out of p may be relevant for discrimination, data dimensionality should be reduced for robust and effective discrimination.
We here introduce a forward sequential selection algorithm and a PCA-based algorithm, as well as a cross-validation scheme that calculates the classification error, optimizes algorithm parameters and determines a classification model. The cross-validation error predicts the classifier's online performance.
3.1 Cross-validation scheme
The cross-validation error used to evaluate the down-selection algorithms’ performance was calculated through a 10-fold double-loop cross-validation scheme. The optimal number of features to select (input parameter of the proposed algorithms) is optimized in the inner cross-validation loop. The performance of the classifier previously trained with the selected features, is validated in the outer loop. Therefore, 10 validation error values are calculated. However, the 10-fold cross-validation results are considerably affected by variability. For this reason, the whole procedure was repeated 10 times. The median of the 100 validation error values (10-fold × 10 repetitions) was defined as the estimate of the classification online performance using the selected features.
A new feature subset was calculated at every validation fold. The number of times that each feature is selected for validation is indicative of its relevance for discrimination. Likewise, channel discriminative ability is assessed by its frequency of selection. A channel is deemed selected when at least one of its particular features (either ERPs or PRs) is selected.
3.2 Linear discriminant classifier
A form of Fisher Discriminant Analysis that was shown to be robust for spatiotemporal EEG pattern discrimination was applied [28]. The canonical discrimination function z is the result of a linear transformation of the original data Y according to Eq. 3. The discrimination coefficients of the canonical discrimination function are denoted by the vector a:
| (3) |
The discrimination coefficients in a were calculated according to calculations described in the Appendix. The Y matrices were determined by the feature selection algorithms for each cross-validation fold.
The discrimination quality was assessed through three different measures: cross-validated error rate for group membership prediction of every p-variate sample; Wilks’ statistic and its normal theory confidence limits; and a bootstrapped confidence limit that is robust against deviations from normality in the data structure [10]. The multivariate data matrix Y is transformed to the vector z which has mean u and a normal p-variate distribution f(z). Prior probabilities πj are calculated as the ratio of the samples within group j to the total number of samples n. According to the Bayesian theory, the probability that the data came from group j of two groups (in our case left-hand or right-hand movement imagery), given a vector z, is calculated through πjz in Eq. 4:
| (4) |
The term πjfj(z) was approximated by exp[q(z)] where [10]. The mean of the canonical discrimination function for group j is uj. The highest πjz determined the predicted group membership for each sample. In order to robustly assess discrimination quality, the cross-validated prediction error rate was calculated. The normal theory Wilks’ statistic (W) analyses the eigenvalues of the linear transformation Ya above. Since W is chi-squared distributed, the discrimination significance was assessed by comparing W with the 95% confidence limit. The statistic W approaches the value zero as the group separation improves. As our data certainly deviate from normality, discrimination quality was also tested through a re-sampling technique (bootstrap) that permutes the data labeling to test whether the group assignment is meaningful. The confidence limit of a classification error was set to 95% of the 100 permutations that were tested. Further details on the discrimination quality measures can be found in [28].
3.3 Sequential forward selection algorithm
This method resulted in a wrapper-type algorithm since a feature is included in subset i if it leads to the highest group discrimination (lowest Wi) of the canonical function zi among all remaining features. The four main steps of this algorithm are described below:
1. First feature selection
the correlation values between the transformed data vector zp (obtained from all p features) and the actual p feature vectors (columns of Y) are called the structural coefficients of zp [4]. The structural coefficients represent the discriminative power of each feature when it is considered for discrimination independent of the p-1 remaining features. The feature with the highest structural coefficient is selected first as Y1. z1 and W1 are calculated.
2. Feature selection loop
In each loop iteration i (i = 2,..., p), the candidate feature to be selected is the feature that jointly with the one(s) selected in the previous i-1 iterations, achieves the highest group discrimination (the lowest Wi). If Wi < Wi - 1 and is significant at the 95% confidence level, the candidate feature is included in Yi. zi is also calculated for each iteration.
3. Loop stop criterion
The feature selection loop stops when no feature can increase the group discrimination any further (any Wi+1 > Wi) or all the p features have already been selected.
4. Selected feature subset
the number of features q to include in the optimal feature matrix Yn×q is optimized in the cross-validation procedure. The optimal feature subset equals the feature set of iteration i = q.
3.4 Across-group variance algorithm
This proposed filter-type method uses a special formulation of PCA [6] to select features while reducing data dimensionality. Initially, Y is decomposed through singular value decomposition (SVD) into three matrices: Un×c (component orthogonal matrix; c is the number of principal components), Sc×c (singular value diagonal matrix), and Vp×c (eigenvector orthogonal matrix; p is the number of features). The eigenvalue vector λ of the feature covariance (YTY) is calculated as the diagonal of S2. The principal components are linear projections of the features onto the orthogonal directions that best describe the data set variance. However, when data presents a group structure, the information provided by a component is more detailed than a variance value. Thus, the total covariance (ψ) can be decomposed into a sum of within (ψwithin) and between (ψbetween) group covariance parts. The pooled covariance matrix is used as an estimation of the within group covariance matrix (ψwithin) as in Eq. 5:
| (5) |
By using the Bessel's correction, the sample covariance matrix ψi is weighted by ni – 1 (ni is the number of samples belonging to the ith group) instead of ni in order to correct the estimator bias (ψi has rank ni – 1 at most). The variance information provided by a principal component in vector notation is deduced in Eq. 6:
| (6) |
where vj is the jth eigenvector (a column of Vp×c matrix) and corresponds to eigenvalue λj. While is a function of the sample distances to their respective group mean, is a function of the distances between the respective group means. In the discrimination context, only the latter comprises useful variance information. Therefore, the distance between groups given by the ith component, normalized by its total variance, gives a relative measure to calculate the AGV as in Eq. 7:
| (7) |
The between group covariance matrix (ψbetween) is calculated fromψ – ψwithin.
Although the principal components are organized by decreasing order of total variance (eigenvalues λi), this order is optimized for orthogonality rather than discrimination between groups. Therefore, the components are ordered according to the across group variance (AGV) in order to take the data group structure into account.
The dimensionality reduction results from the truncation of the c principal components ranked by decreasing AGV. The truncation criterion is a cumulative sum percentage of the descending ordered AGV scores and was assigned threshold values (typically 60–90%) for variance truncation [16]. The optimal threshold value was found by cross-validation. If k components met the truncation criterion, the truncated component matrix Un×k (k < c) is a lower dimensional representation of the original feature space and more suitable for group discrimination. The retained variance information was transformed back to the original feature space using a modified version of the spectral decomposition property as in Eq. 8. In order to determine the features which resemble the retained components with minimal information loss, an across-group covariance matrix (ψAGV) was calculated:
| (8) |
Note that AGVi is used instead of λi in the spectral decomposition Eq. 8. Each diagonal value of ψAGV represents the variance of a particular feature accounted for by the k retained principal components and measures feature discriminability. A ranked list with all p features in descending order of discriminability was determined. Finally, the number (q) of features that determine the optimal feature matrix Yn×q was optimized by cross-validation.
4 Feature selection in common use
The accuracy of PR classification and the features selected were evaluated for the proposed algorithms (SFS and AGV) and three other feature selection algorithms in common use. The recursive feature elimination (RFE) algorithm, which is a wrapper method, uses the feature weights of the support vector machine (SVM) training process to perform backward feature elimination [20]. The relief algorithm, which is a filter method, assigns a relevance value to each feature producing a ranking [24]. The GA, which is a global search algorithm, is a wrapper method and was implemented according to Fatourechi et al. [9].
5 Results
Table 1 provides the median cross-validation error and median number of features selected from 100 folds in the cross-validation scheme. This table also provides the number of folds whose discrimination was significant through the Wilks’ statistic with 95% confidence. The classification accuracies that were significant by the bootstrap method are highlighted in bold face.
Table 1.
Results of left versus right hand, movement imagery task discrimination for Experiment 1 when power ratio (PR) features were extracted
| Subject code | SFS |
AGV |
RFE |
GA |
Relief |
|||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Nfeat | NW < 95% | Error | Nfeat | NW < 95% | Error | Nfeat | Error | Nfeat | Error | Nfeat | |
| (a) Common-average reference | ||||||||||||
| A | 33.33 | 9 | 100 | 14.29 | 5 | 100 | 32.67 | 62 | 37.24 | 45 | 41.58 | 48 |
| B | 62.50 | 11 | 100 | 16.67 | 5 | 99 | 44.90 | 45 | 49.25 | 45 | 45.85 | 44 |
| C | 25.00 | 3 | 100 | 12.50 | 5 | 100 | 29.64 | 86 | 32.94 | 46 | 46.12 | 37 |
| D | 50.00 | 7 | 100 | 28.57 | 1 | 67 | 53.27 | 20 | 49.83 | 45 | 51.81 | 55 |
| E | 50.00 | 12 | 100 | 33.33 | 5 | 40 | 47.94 | 37 | 50.83 | 45 | 49.57 | 46 |
| Mean | 44.17 | 8.4 | 100 | 21.07 | 4.2 | 81.2 | 41.68 | 50 | 44.02 | 45.2 | 46.99 | 46 |
| (b) Laplacian spatial filtering | ||||||||||||
| A | 28.57 | 10 | 100 | 14.29 | 4 | 100 | 36.35 | 64 | 37.86 | 45 | 43.42 | 48 |
| B | 50.00 | 7 | 100 | 16.67 | 4 | 99 | 41.82 | 50 | 45.74 | 46 | 44.85 | 26 |
| C | 14.29 | 3 | 100 | 12.50 | 4 | 99 | 25.81 | 91 | 33.02 | 46 | 45.32 | 58 |
| D | 50.00 | 13 | 100 | 38.09 | 5 | 67 | 48.64 | 39 | 47.26 | 45 | 47.99 | 61 |
| E | 50.00 | 1 | 100 | 28.57 | 5 | 55 | 56.36 | 32 | 52.78 | 45 | 49.89 | 39 |
| Mean | 38.57 | 6.8 | 100 | 22.02 | 4.4 | 84 | 41.8 | 55.2 | 43.33 | 45.4 | 46.29 | 46.4 |
The median of the cross-validated classification error, the median of the number of features selected per validation fold (Nfeat), and the number of cross-validation folds whose classification was significant according to the Wilks’ statistic (NW < 95%) at the 95% confidence level, are presented for all tested algorithms (SFS, AGV, RFE, GA, and RELIEF). Data were re-referenced using common-average reference (top table) and Laplacian spatial filtering (bottom table). The error values in bold represent discriminations that were significant through the bootstrap method
5.1 Algorithm comparison
The PRs were used for comparison of the proposed feature selection algorithms (SFS and AGV) with three other algorithms in common use (RFE, GA, and relief) to discriminate movement imagery responses. Table 1a (common-average reference) and b (Laplacian spatial filter) presents the PR classification errors for all tested feature selection algorithms and demonstrate that AGV algorithm performed better than the other algorithms. The AGV algorithm achieved cross-validation errors between 12.5% and 38.09%, selecting only 4 of 95 available PRs, on average. Although the SFS algorithm performed similarly to the RFE algorithm, the former only selected 8 (common-average) and 7 (Laplacian) PRs while RFE selected 50 (common-average) and 55 (Laplacian) PRs. The GA and relief algorithms ranked next in increasing error. The AGV algorithm achieved lower error values and selected fewer features than the SFS algorithm in most cases. However, while the SFS algorithm achieved discriminations that were significant through the Wilks’ statistic in every cross-validation fold, the AGV algorithm discriminations were less significant. Thus, SFS and AGV algorithms demonstrated particular strengths.
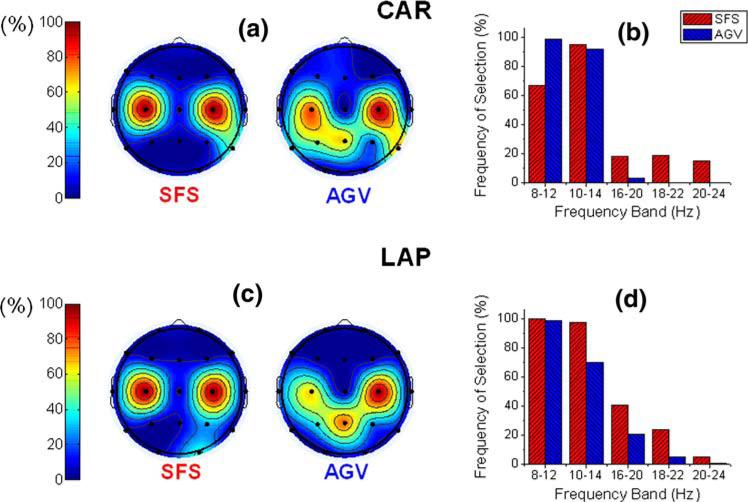
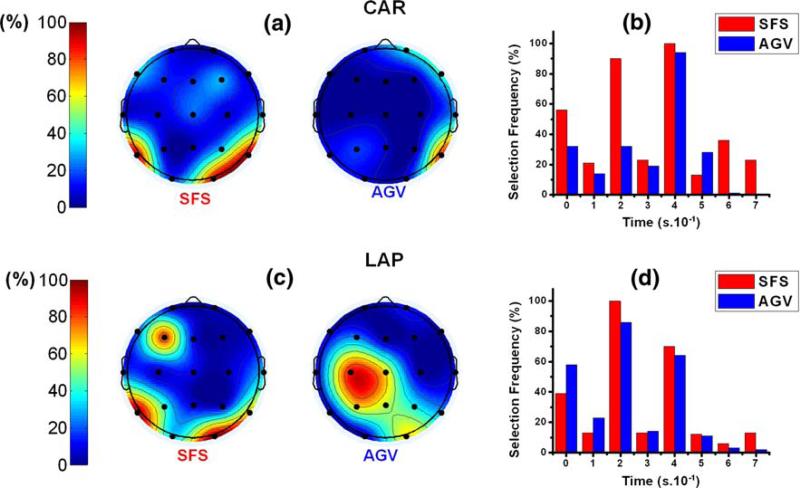
The feature selection of the proposed algorithms was evaluated in terms of EEG channels and PRs in specific frequency ranges. As illustrated in Fig. 3a and c, central channels C3 and C4 were frequently selected by both proposed algorithms to discriminate between left and right hand movement imageries. The parietal channels P3, Pz, and P4 were also relevant for the left versus right hand movement imagery discrimination when the AGV algorithm was applied. The frequency bands 8–12 and 10–14 Hz were selected by both algorithms for most of the validations, as illustrated in Fig. 3b and d.
Fig. 3.
Feature selection frequency for discrimination of left versus right hand movement imagery calculated by SFS and AGV algorithms from Subject C data. Blue represents AGV results and red represents SFS algorithm results. Features are organized as EEG channels in (a) and (c) and as frequency bands in (b) and (d). Common-average re-referenced (CAR) data were used in (a) and (b). Laplacian (LAP) re-referencing method was used in (c) and (d)
5.2 Event-related potential discrimination
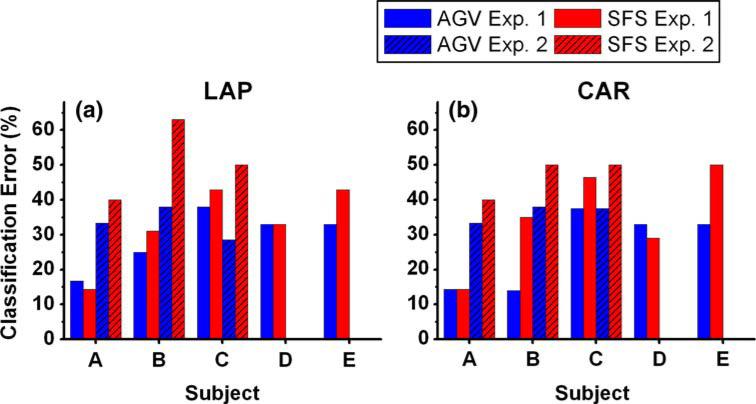
The proposed feature selection algorithms were also applied on the discrimination of ERPs in response to arrangements of the movement cues (left and right arrows). While five subjects agreed to participate in Experiment 1 (same data as in PR analysis), only three of them underwent the Experiment 2. The arrows in Fig. 2a and b cued subjects in Experiment 1. Although, as in Experiment 1, the cues pointed either to the left or to the right, they were balanced across the visual field in Experiment 2 (Fig. 2c and d). The cue changes were employed in order to detect possible perception related EEG responses [21, 31]. Figure 4 compares cross-validated classification errors from both experiments and demonstrates that Experiment 2 generally led to a classification error increase (except for Subject C with AGV algorithm). Classification performance degradation was observed for both re-referencing methods.
Fig. 4.
Cross-validated classification errors (%) of event-related responses to left versus right hand cues in both Experiment 1 and Experiment 2. Only three subjects (A, B, and C) participated in both experiments. Data were re-referenced using both the a Laplacian spatial filter and the b common-average reference
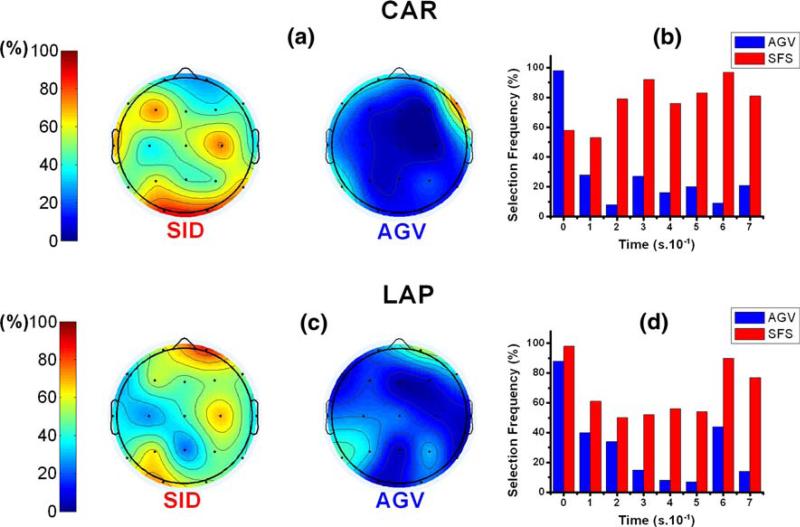
In Experiment 1, the introduced algorithms down-selected feature spaces from 152 to less than 13 ERPs with cross-validation errors between 14% and 33%. The selection of ERPs in response to left versus right hand movement cues is illustrated in Fig. 5 for Experiment 1 and in Fig. 6 for Experiment 2. Considering both re-referencing methods, the channels F3, C3, P7, P8, and O2 were most relevant for discrimination in Experiment 1, for Subject A. Additionally, parietal (e.g., P7 and P8) and occipital channels (e.g., O1 and O2) were often selected among subjects in Experiment 1. According to the results of AGV algorithm (Figs. 5a, c, 6a, and d), the selection frequency of channels P7, P8, O1, and O2 decreased in Experiment 2. Although the results of the SFS algorithm demonstrate a less accentuated decrease on the frequency selection of such channels between experiments, a decrease in selection specificity was observed in Experiment 2. While ERPs with latencies 200 and 400 ms were selected frequently in Experiment 1 (Fig. 5b, d), no latency was particularly selected in Experiment 2.
Fig. 5.
Feature selection frequency for the discrimination of event-related responses to left versus right hand cues, for Subject A, in Experiment 1. Both AGV(blue) and SFS (red) algorithms results are presented. Features are organized as EEG channels in (a) and (c) and as time points in (b) and (d). Common-average re-referenced (CAR) data were used in (a) and (b). Laplacian (LAP) re-referencing method was used in (c) and (d)
Fig. 6.
Feature selection frequency for the discrimination of event-related responses to left versus right hand cues, for Subject A, in Experiment 2. Both AGV (blue) and SFS (red) algorithms results are presented. Features are organized as EEG channels in (a) and (c) and as time points in (b) and (d). Common-average re-referenced (CAR) data were used in (a) and (b). Laplacian (LAP) re-referencing method was used in (c) and (d)
6 ERP waveforms
In order to identify ERPs in response to left and right hand movement cues, data epochs from 200 ms before the visual stimulus onset (i.e., left or right arrow) to 800 ms post-stimulus were analysed. The segments were averaged across trials per task. An ERP in response to visual stimulation of a hemi-field is lateralized with respect to a unilateral stimulus (either left or right arrow) [31]. However, other ERPs with no lateral spatial distribution might also be detected. The event-related lateralization (ERL) is a useful transformation often employed to isolate ERP components that are lateralized and is calculated similarly to lateralized readiness potential [31]. The lateralized potentials are calculated for symmetric channel locations according to Eq. 9 (example for the channel pair C4–C3) where L and R stand for left and right arrows respectively. Thus, for each arrow, the averaged ERP of an EEG channel ipsi-lateral to the arrow is subtracted from the averaged ERP of an EEG channel contra-lateral to the arrow. The ERL is calculated by averaging the subtractions resultant for both tasks:
| (9) |
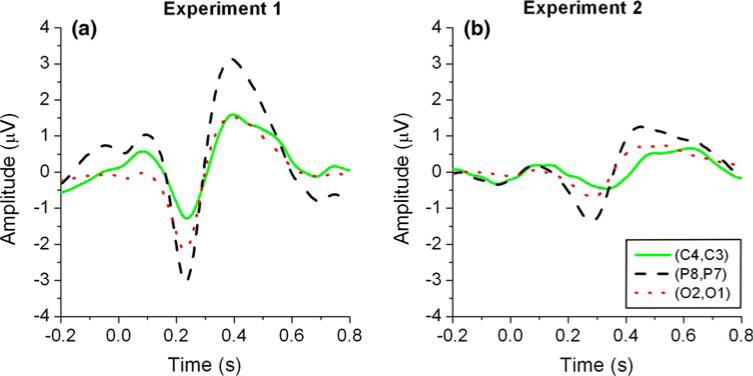
Event-related lateralization waveforms were calculated for the symmetric channel pairs C4–C3, P8–P7, and O2–O1 in Experiment 1 (Fig. 7a) and Experiment 2 (Fig. 7b) for Subject A. A negative deflection between 150 and 350 ms poststimulus on the ERL waveforms depicts an ERP that was reactive to stimulus differences. This ERP is contra-lateral to the stimulus and, in Experiment 1, was more evident in the channel pairs P8–P7 and O2–O1 compared to the channel pair C4–C3 (see Table 2). The employment of visual cues balanced in the visual field dramatically reduced the amplitude and increased the latency of the deflection in Experiment 2, particularly on channel pairs P8–P7 and O2–O1. As a result, the decrease in amplitude found on ERL waveforms from Experiment 1 to Experiment 2 appears to be the main factor contributing to the classification error increase, as illustrated on Fig. 4.
Fig. 7.
Event-related lateralization for left versus right arrows calculated for the channel pairs C4–C3, P8–P7, and O2–O1 from Subject A data in Experiment 1 (a) and Experiment 2 (b). Data have been previously re-referenced to common-average
Table 2.
Latency and amplitude values of the event-related lateralization (ERL) minima for left versus right movement imagery between 150 and 350 ms after stimulus presentation
| Experiment | C4–C3 |
P8–P7 |
O2–O1 |
|||
|---|---|---|---|---|---|---|
| Latency (ms) | Amplitude (μV) | Latency (ms) | Amplitude (μV) | Latency (ms) | Amplitude (μV) | |
| 1 | 234 | –1.28 | 230 | –3.04 | 230 | –2.16 |
| 2 | 332 | –0.46 | 281 | –1.37 | 285 | –0.71 |
Results from Subject A were presented for the three symmetric channel pairs C4–C3, P8–P7, and O2–O1 from both experiments
7 Discussion
This study introduces two novel algorithms to down-select features for BCI applications. The proposed feature selection algorithms were compared with three other popular algorithms to select relevant PRs for discrimination of left versus right hand movement imagery performance. The AGV algorithm performed the best among all the other algorithms that were tested. AGV achieved classification errors between 12.5% and 38.1% with feature dimensionality reductions of more than 95%. Although SFS and RFE algorithms achieved similar classification accuracies, the former selected smaller feature subsets. The GA and relief algorithms ranked next in increasing error. Besides the best classification accuracy, the AGV algorithm ran six times faster than the SFS algorithm and eight times faster than the RFE algorithm.
As a wrapper-type algorithm, iterative selection has been frequently used for sequential feature selection in BCI research with promising results [8, 19]. Although the running time of the classifier is multiplied by a factor of m2 (m being the number of features), algorithms such as SFS and RFE are becoming more practical due to the increasing computational power of laboratory grade computers. Additionally, such algorithms are straightforward to implement. The SFS algorithm selects features based on the Wilks’ statistic which uses the eigenvalues of the transformation matrix calculated by an LDA classifier. Instead of assessing a confidence value of the F-statistic as the standard stepwise stop criterion [7], the number of features to include in the classification model was optimized in a cross-validation loop. Therefore, this parameter could be customized for each subject based on the classification error. The applicability of the SFS algorithm to more than two data groups is straightforward since it relies on the LDA classifier ability to generalize for any number of groups [10].
The proposed AGV algorithm is based on a formulation of PCA with supervised learning. PCA has been widely used as a dimension reduction technique in BCI research [25]. The proposed AGV algorithm uses principal components to down-select original features thus reducing computational complexity. Features are ranked according to their AGV in a truncated component space. Ranking algorithms usually order features according to a relevance criterion but ignore the context of other features [14]. However, in the AGV algorithm, feature ranking implicitly considers the context of other features since a principal component is a linear combination of all features. As in the SFS algorithm, the number of features selected was optimized on a subject-basis in a cross-validation loop. The AGV score directly generalizes for more than two groups since the between group covariance matrix can be equally calculated for any number of groups.
The comparison of the two introduced methods reveals distinct results. The Wilks’ test of significance revealed that discriminations calculated through the SFS algorithm were more significant than the AGV algorithm's. However, the AGV achieved lower cross-validation errors than SFS. As these results suggest, although the feature subsets computed through the SFS algorithm represented best the data used to train the classifier, they did not describe previously unseen data as well as the features calculated by the AGV algorithm. Moreover, in this study, the SFS algorithm selected more features than the AGV algorithm. On the one hand, smaller feature subsets contribute to less complex classification models which may increase model adaptability to new data. On the other hand, larger feature subsets retain more information about subject-specific EEG patterns and can benefit from low intertrial variability on the task-related responses.
In movement imagery discrimination, the frequency ranges 8–12 and 10–14 Hz on the C3 and C4 EEG channels were frequently selected by both proposed algorithms which reflects the reactivity of the “rolandic mu rhythm” to movement imagery tasks [32]. The discrimination relevance of some posterior channels (e.g., parietal and occipital locations) has also been reported earlier and appears related to the concurrent visual input of instructing cues [1].
Event-related potentials in response to left versus right movement cues were also discriminated in a trial basis. The proposed algorithms achieved classification errors between 14% and 33% with feature dimensionality reductions of more than 90%, when symmetric cues were employed (Experiment 1). While channels at parietal (e.g., P7 and P8) and occipital (e.g., O1 and O2) sites were selected frequently among subjects in Experiment 1, such channels were barely selected or with less specificity in Experiment 2. The investigated ERL waveforms demonstrated a contra-lateral component between 150 and 350 ms post-stimulus, prominent at parietal and occipital sites. Our results demonstrate that this component was modulated by visual stimuli parameters since it demonstrated higher amplitudes in Experiment 1 than in Experiment 2 [15], and demonstrated higher latency in Experiment 2. Similar parietal and occipital ERPs have been associated with brain mechanisms dependent on visual spatial attention [21, 31] and/or movement intention [13, 30]. Although the amplitudes of such ERPs were largely attenuated by the presentation of balanced arrows, which suggests the manifestation of a visual spatial mechanism, the residual direction-congruent potentials on parietal and occipital channels (Fig. 7b) might also unveil a movement intention mechanism [30]. The detection of these cue-evoked potentials was most prominent on P7, P8, O1, and O2 channels and confirms that the subject is indeed fixating and giving attention to the BCI paradigm. Therefore, this physiology might be used as a “gate” mechanism of the classification algorithm to validate the detection of a motor imagery event.
In conclusion, the proposed feature selection algorithms demonstrated their value for discrimination of both movement imagery tasks and cue-evoked responses by increasing classification accuracy, reducing the number of required EEG channels, and reducing computation times. In addition, use of sensory evoked potentials to detect fixation and attention, and the required causal time lags to motor intention, offer creative prospects to improve BCI [13].
Acknowledgments
The project described was supported by Award Number K25NS061001 from the US National Institute Of Neurological Disorders And Stroke. N. S. Dias was supported by the Portuguese Foundation for Science and Technology under the grant SFRH/BD/21529/2005. S. J. Schiff was supported by the NIH grant K02MH01493, The Pennsylvania Keystone Innovation Zone Program and The Pennsylvania Tobacco Settlement. The authors acknowledge the contribution of L.R. Jacinto on method implementation.
Appendix
This appendix describes the calculation of the discrimination coefficients a employed in:
Considering that z is the discrimination function and Y is the feature matrix. Initially, the SVD of the within-group covariance matrix W is calculated as:
S is a diagonal matrix, and U appears twice since covariance matrices are symmetric. B is the between-group covariance matrix. In order to obtain a better coordinate system, the vector a in the following Fisher criterion:
is replaced by US−1/2UTv; resulting in:
In general, for a symmetric matrix H, the maximum of vTHv is attained for the first singular vector v = v1. Similarly, the maximization of α may be calculated through the following SVD:
The maximum of α is , is the highest singular value of H. Converting back to original coordinates a:
which is equivalent to the first column of US−1/2UTV.
Contributor Information
N. S. Dias, Department of Industrial Electronics, University of Minho, Campus Azurem, 4800-058 Guimaraes, Portugal
M. Kamrunnahar, Center for Neural Engineering, Department of Engineering Sciences and Mechanics, The Pennsylvania State University, University Park, PA 16802, USA
P. M. Mendes, Department of Industrial Electronics, University of Minho, Campus Azurem, 4800-058 Guimaraes, Portugal
S. J. Schiff, Center for Neural Engineering, Department of Engineering Sciences and Mechanics, The Pennsylvania State University, University Park, PA 16802, USA Department of Neurosurgery and Physics, The Pennsylvania State University, University Park, PA 16802, USA.
J. H. Correia, Department of Industrial Electronics, University of Minho, Campus Azurem, 4800-058 Guimaraes, Portugal
References
- 1.Babiloni C, et al. Human movement-related potentials vs desynchronization of EEG alpha rhythm: a high-resolution EEG study. NeuroImage. 1999;10:658–665. doi: 10.1006/nimg.1999.0504. [DOI] [PubMed] [Google Scholar]
- 2.Bashashati A, Ward RK, Birch GE. A new design of the asynchronous brain–computer interface using the knowledge of the path of features.. Proc 2nd IEEE-EMBS conference on neural engineering; Arlington, VA. 2005. pp. 101–104. [Google Scholar]
- 3.Boostani R, et al. A comparison approach toward finding the best feature and classifier in cue-based BCI. Med Biol Eng Comput. 2007;45:403–412. doi: 10.1007/s11517-007-0169-y. [DOI] [PubMed] [Google Scholar]
- 4.Courville T, Thompson B. Use of structure coefficients in published multiple regression articles: β is not enough. Educ Psychol Meas. 2001;61:229–248. [Google Scholar]
- 5.Dias NS, et al. Feature Down-Selection in brain–computer Interfaces.. Proc. of the 4th international IEEE EMBS conference on neural engineering.; Antalya, Turkey. 2009. pp. 323–326. [Google Scholar]
- 6.Dillon WR, Mulani N, Frederick DG. On the use of component scores in the presence of group structure. J Cons Res. 1989;16:106–112. [Google Scholar]
- 7.Duda RO, Hart PE, Stork DG. Pattern classification. Wiley; New York: 2001. [Google Scholar]
- 8.Fabiani GE, et al. Conversion of EEG activity into cursor movement by a brain–computer interface (BCI). IEEE Trans Neural Syst Rehabil Eng. 2004;12:331–338. doi: 10.1109/TNSRE.2004.834627. [DOI] [PubMed] [Google Scholar]
- 9.Fatourechi M, et al. Automatic user customization for improving the performance of a self-paced brain interface. Med Biol Eng Comput. 2006;44:1093–1104. doi: 10.1007/s11517-006-0125-2. [DOI] [PubMed] [Google Scholar]
- 10.Flury B. A first course in multivariate statistics. Springer; New York: 1997. [Google Scholar]
- 11.Grafton ST, et al. Premotor cortex activation during observation and naming of familiar tools. Neuroimage. 1997;6:231–236. doi: 10.1006/nimg.1997.0293. [DOI] [PubMed] [Google Scholar]
- 12.Guger C, et al. Rapid prototyping of an EEG-based brain–computer interface (BCI). IEEE Trans Neural Syst Rehabil Eng. 2001;9:49–58. doi: 10.1109/7333.918276. [DOI] [PubMed] [Google Scholar]
- 13.Guo F, et al. A brain–computer interface using motion-onset visual evoked potential. J Neural Eng. 2008;5:477–485. doi: 10.1088/1741-2560/5/4/011. [DOI] [PubMed] [Google Scholar]
- 14.Guyon I, Eliseeff A. An introduction to variable and feature selection. J Mach Learn Res. 2003;3:1157–1182. [Google Scholar]
- 15.Hillyard SA, Vogel EK, Luck SJ. Sensory gain control (amplification) as a mechanism of selective attention: electro-physiological and neuroimaging evidence. Phil Trans R Soc Lond B. 1998;353:1257–1270. doi: 10.1098/rstb.1998.0281. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Jolliffe IT. Principal component analysis. Springer; New York: 2002. [Google Scholar]
- 17.Klemm M, Haueisen J, Ivanova G. Independent component analysis: comparison of algorithms for the investigation of surface electrical brain activity. Med Biol Eng Comput. 2009;47:413–423. doi: 10.1007/s11517-009-0452-1. [DOI] [PubMed] [Google Scholar]
- 18.Kruglikov SY, Schiff SJ. Interplay of EEG phase and auditory evoked neural activity. J Neurosci. 2003;2:10122–10127. doi: 10.1523/JNEUROSCI.23-31-10122.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Krusienski DJ, et al. Toward enhanced P300 speller performance. J Neurosci Meth. 2008;167:15–21. doi: 10.1016/j.jneumeth.2007.07.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Lal TN, et al. Support vector channel selection in BCI. IEEE Trans Biomed Eng. 2004;51:1003–1010. doi: 10.1109/TBME.2004.827827. [DOI] [PubMed] [Google Scholar]
- 21.Lee P-L, et al. Brain computer interface using flash onset and offset visual evoked potentials. Clin Neurophysiol. 2008;119:605–616. doi: 10.1016/j.clinph.2007.11.013. [DOI] [PubMed] [Google Scholar]
- 22.Liao X, et al. Combining spatial filters for the classification of singal-trial EEG in a finger movement task. IEEE Trans Biomed Eng. 2007;54:821–831. doi: 10.1109/TBME.2006.889206. [DOI] [PubMed] [Google Scholar]
- 23.Luck SJ. An introduction to the event-related potential technique. The MIT Press; Cambridge, MA: 2005. [Google Scholar]
- 24.Millán J, et al. Relevant EEG features for the classification of spontaneous motor-related tasks. Biol Cybern. 2002;86:89–95. doi: 10.1007/s004220100282. [DOI] [PubMed] [Google Scholar]
- 25.Müller T, et al. Selecting relevant electrode positions for classification tasks based on the electro-encephalogram. Med Biol Eng Comput. 2000;38:62–67. doi: 10.1007/BF02344690. [DOI] [PubMed] [Google Scholar]
- 26.Pfurtscheller G, Neuper C. Motor imagery and direct brain–computer communication. Proc IEEE. 2001;89:1123–1134. [Google Scholar]
- 27.Schiff SJ. Dangerous phase. Neuroinformatics. 2005;3:315–318. doi: 10.1385/NI:03:04:315. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Schiff SJ, et al. Neuronal spatiotemporal pattern discrimination: the dynamical evolution of seizures. Neuroimage. 2005;28:1043–1055. doi: 10.1016/j.neuroimage.2005.06.059. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Sun S, Zhang C. Adaptive feature extraction for EEG signal classification. Med Biol Eng Comput. 2006;44:931–935. doi: 10.1007/s11517-006-0107-4. [DOI] [PubMed] [Google Scholar]
- 30.Wang Y, Makeig S. Predicting intended movement direction using EEG from human posterior parietal cortex. In: Schmorrow DD, et al., editors. Augmented cognition, HCII 2009. LNAI 5638; 2009. pp. 437–446. [Google Scholar]
- 31.Wascher E, Wauschkuhn B. The interaction of stimulus- and response-related processes measured by event-related lateralizations of the EEG. Electroencephalogr Clin Neurophysiol. 1996;99:149–162. doi: 10.1016/0013-4694(96)95602-3. [DOI] [PubMed] [Google Scholar]
- 32.Wolpaw JR, et al. Brain–computer interfaces for communication and control. Clin Neurophysiol. 2002;113:767–791. doi: 10.1016/s1388-2457(02)00057-3. [DOI] [PubMed] [Google Scholar]
- 33.Wolpaw JR, McFarland DJ. Control of a two-dimensional movement signal by a noninvasive brain–computer interface in humans. Proc Natl Acad Sci USA. 2004;101:17849–17854. doi: 10.1073/pnas.0403504101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Yu L, Liu H. Efficient feature selection via analysis of relevance and redundancy. J Mach Learn. 2004;5:1205–1224. [Google Scholar]