Abstract
We introduce the python software package Kernel Mixed Model (KMM), which allows users to incorporate the network structure into transcriptome-wide association studies (TWASs). Our software is based on the association algorithm KMM, which is a method that enables the incorporation of the network structure as the kernels of the linear mixed model for TWAS. The implementation of the algorithm aims to offer users simple access to the algorithm through a one-line command. Furthermore, to improve the computing efficiency in case when the interaction network is sparse, we also provide the flexibility of computing with the sparse counterpart of the matrices offered in Python, which reduces both the computation operations and the memory required.
Keywords: gene-set prioritization, linear mixed model, transcriptome association
1. INTRODUCTION
The association mapping between gene expressions and phenotypes offers the community an opportunity to understand the functional relevance of genes to the traits of interest. Although this topic has been investigated for decades (Ding and Peng, 2005; Meinshausen and Bühlmann, 2010; Zou and Hastie, 2005), it recently becomes important again as one essential step in Transcriptome-wide Association Study (TWAS) (Barbeira et al, 2018; Gamazon et al, 2015; Gusev et al, 2016) to continue the endeavor to investigate the missing heritability of complex traits. In this article, we aim to introduce a software that facilitates the study of the association between transcritome and phenotypes.
Our contribution follows a simple idea that incorporating the network structure of genes will likely improve the association study. Although this idea was explored a decade ago (Li and Li, 2008), and has been extensively followed up in machine learning and data science community, we notice that the resultant software has not been widely adopted by geneticists. One possible reason behind the insufficient usage of these software that can incorporate the network structure knowledge into association study is that these software do not provide an estimation of the statistical significance of the discovered association, probably due to the fact that introducing structural knowledge through regularization greatly increases the statistical difficulty in reporting p-values.
Motivated by the importance of TWAS, and the necessity of introducing an association method that can incorporate the network structure and report p-values, we introduce the Kernel Mixed Model (KMM) software implementing the KMM described in Wang et al (2022).
2. IMPLEMENTATION DETAILS AND EFFICIENCY EXPERIMENTS
In addition to the implementation of the algorithmic contribution reported in Wang et al (2022), we also add a few new functions to overcome possible usage barriers one may encounter in using our software in practice. In particular, we add functions that address the following challenges in the implementation: (1) the possibility that the Laplacian matrix that the software needs to inverse based on our algorithm is uninvertible, and (2) the fact that operations over dense matrices may take significantly longer time than sparse matrices.
2.1. Approximating the inverse of a matrix and corresponding experiments
Our algorithm requires one operation of the inverse of the normalized Laplacian matrix for the calculation of the kernel of the mixed model, where the Laplacian matrix is obtained from the network structure. However, in practice, we notice that not all the Laplacian matrices (constructed from various of network structures) are full rank (thus, not all of them are invertible). Therefore, a vanilla usage of the Python matrix inverse operation will lead to an error message and termination of the computation.
Fortunately, since we only need to inverse the normalized Laplacian matrix, of which eigenvalues are all <1, we can safely implement the following procedure to approximate the calculation of the inverse matrix:
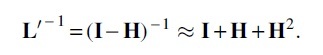
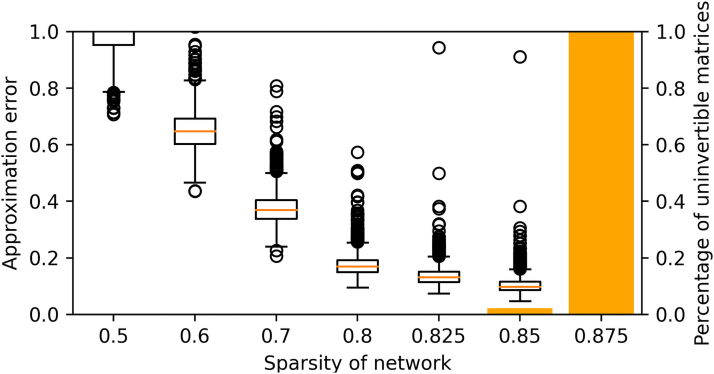
To have a quantitative understanding of the advantages and the limitations of this approximation, we test the error of this approximation in terms of the mean squared errors of the elements of the resultant matrices and report the result in Figure 1.
FIG. 1.
The error of approximation (box plot) and the percentage of uninvertible matrices (bar plot) at different sparsity levels of the matrix.
In our experiment, we compare the differences of inversing 1000 matrices for each of the sparsity levels listed in Figure 1, where the x-axis denotes the fraction of zeros over all elements in the matrix. Our results show that as the sparsity level increases, the matrix is less likely invertible (thus, our implementation is more important), and also that the approximation error gets smaller.
It is worth mentioning that we believe, in practice, the network structure is highly sparse, which means the corresponding Laplacian matrix is likely uninvertible, and thus our implementation is essential. However, even in the situation where the Laplacian matrix is invertible, the introduced approximation error is fairly small as shown in Figure 1.
2.2. Sparse matrix implementation and corresponding experiments
Another challenge we notice is that the memory required to store the network information scales quadratically with the number of all genes to be tested, even though there are much fewer genes in the network. Thus, to avoid the unnecessary usage of the memory when the matrix is sparse and to accelerate the computation, we implement the sparse version of the KMM. To encourage the usages, the software will automatically detect whether it will run the sparse version or the original version given the input network structure.
To demonstrate the effectiveness of using the sparse version of the implementation, we run a simple experiment to compare the run time of the matrix multiplication using the original matrix implementation and the sparse counterpart, respectively. We notice that over 1000 runs of multiplying matrices, the sparse implementation is 2000 orders of faster on average than the original implementation when the input matrix is indeed sparse.
3. USAGE INSTRUCTIONS
Users can download or install the software from https://github.com/HaohanWang/KMM, and use the software with a simple command line:
$ python kmm.py –gene <expression values> \
–pheno <phenotype values> \
–net <network structure> \
–cov <covariate values to regress out> \
–out <output file>
where files for gene expressions, phenotypes, and covariates (optional) are csv files with headings. The network structure file is expected to be lines of gene names. For each line, the first gene is connected with the remaining genes.
ACKNOWLEDGMENTS
We are thankful for the constructive comments we get when presenting the algorithm part of this study at Machine Learning for Computational Biology (MLCB) and Research in Computational Molecular Biology (RECOMB).
AUTHOR DISCLOSURE STATEMENT
The authors declare they have no conflicting financial interests.
FUNDING INFORMATION
This study is supported by the National Institutes of Health grant R01GM140467.
REFERENCES
- Barbeira AN, Dickinson SP, Bonazzola R, et al. Exploring the phenotypic consequences of tissue specific gene expression variation inferred from GWAS summary statistics. Nat Commun 2018;9(1):1825; doi: 10.1038/s41467-018-03621-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ding C, Peng H. Minimum redundancy feature selection from microarray gene expression data. J Bioinform Comput Biol 2005;3(2):185–205; doi: 10.1142/s0219720005001004 [DOI] [PubMed] [Google Scholar]
- Gamazon ER, Wheeler HE, Shah KP, et al. A gene-based association method for mapping traits using reference transcriptome data. Nat Genet 2015;47(9):1091–1098; doi: 10.1038/ng.3367 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gusev A, Ko A, Shi H, et al. Integrative approaches for large-scale transcriptome-wide association studies. Nat Genet 2016;48(3):245–252; doi: 10.1038/ng.3506 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li C, Li H. Network-constrained regularization and variable selection for analysis of genomic data. Bioinformatics 2008;24(9):1175–11821367–4803; doi: 10.1093/bioinformatics/btn081 [DOI] [PubMed] [Google Scholar]
- Meinshausen N, Bühlmann P. Stability selection. J R Stat Soc Series B (Stat Methodol) 2010;72(4):417–473. [Google Scholar]
- Wang H, Lopez OL, Wu W, et al. Gene set priorization guided by regulatory networks with p-values through kernel mixed model. In International Conference on Research in Computational Molecular Biology. Springer; 2022; pp. 107–125. [Google Scholar]
- Zou H, Hastie T. Regularization and variable selection via the elastic net. J Royal Stat Soc Series B (Stat Methodol) 2005;67(2):301–320. [Google Scholar]