Towards Magnetic Field Gradient-Based Imaging and Control of In-Body Devices

Hongxiang Gao; Yubin Lin; Manuel Monge

doi:10.1109/biocas49922.2021.9645032

. Author manuscript; available in PMC: 2022 Mar 29.

Published in final edited form as: IEEE Biomed Circuits Syst Conf. 2021 Dec 23;2021:10.1109/biocas49922.2021.9645032. doi: 10.1109/biocas49922.2021.9645032

Towards Magnetic Field Gradient-Based Imaging and Control of In-Body Devices

Hongxiang Gao ¹, Yubin Lin ¹, Manuel Monge ¹

PMCID: PMC8963196 NIHMSID: NIHMS1741076 PMID: 35356802

Abstract

This papers reports a magnetic field gradient-based imaging system for in-body devices which takes inspiration from the localization principles of magnetic resonance imaging. By applying three orthogonal magnetic field gradients, the location of a device inside the body can be determined by measuring the magnetic fields in the device and transmitting this information to an external reader. The proposed system consists of one pair of Helmholtz coils and two pairs of saddle coils and is capable of generating the three orthogonal gradient fields. To emulate an implantable device, a miniature sensor module was designed using off-the-shelf components and semi-passive UHF RFID. The proposed localization system produces magnetic field gradients up to 187.4 G/m while consuming 1 A and achieves an average localization error of 80 μm.

Keywords: magnetic field gradient, gradient, localization, in-body devices, implantable devices, implants

I. Introduction

The miniaturization of medical devices has enabled the development of new approaches for diagnostics and therapeutics. Nowadays, small medical devices can diagnose and treat disease from inside the body targeting neurological and autoimmune disorders, cardiovascular conditions, cancer, and other diseases [1]. The function of such implantable medical devices (IMDs) critically depends on their locations. As their size reduces, locating and communicating with them becomes more challenging due to the smaller size of the implant’s transducer used for these purposes.

Existing technologies to locate and communicate with IMDs are mainly based on RF, ultrasound (US), and light approaches [2]. The mainstream RF localization system uses received signal strength indicator (RSSI)- and time of arrival (TOA)-based multi-receiver arrays [3, 4]. Compared to that of free space, the RF characteristics of tissue introduce significant challenges for RSSI-TOA methods due to its non-homogeneous and high-absorption media, significantly impacting the performance of pulse-driven localization systems [5]. Other approaches include the use of X-ray or US [4, 6]. However, as an ionizing radiation, X-ray poses health risks to both the patients and doctors, thus unsuitable for prolonged tracking operations. Ultrasound, on the other hand, does not possess radiation risk, but its applications are limited to soft tissues [7]. Additionally, US imaging requires constant contact between the transducer and the tissue for good impedance matching. Therefore, a robust, non-ionizing, fully-wireless localization system is needed to support the development of in-body miniaturized wireless implants for novel diagnostics and therapeutics.

In this work, we propose a magnetic field gradient-based imaging system for in-body devices which uses the localization principles of magnetic resonance imaging (MRI); originally proposed in [8]. Our proposed system generates magnetic field gradients in three orthogonal directions via three pairs of Helmholtz and saddle coils as shown in Fig. 1. By measuring the magnetic field in the device, we can determine its location by transmitting this information to an external reader. To emulate an IMD, a miniature sensor module with a 3-dimensional (3-D) magnetic sensor was developed using commercially available components and semi-passive UHF RFID to be used in localization experiments.

Fig. 1. — Magneteic field gradient-based localization system overview

II. Localization System

A. Localization principle

Consider an IMD inside the body in a monotonic magnetic field profile B_X = g(x). By using the principle of spatial encoding through magnetic field gradients, the location of the IMD can be estimated by mapping the measured magnetic field back into space according to:

\hat{x} = g^{- 1} ({\hat{B}}_{X}),

(1)

where g⁻¹ is the inverse function of B_X, ${\hat{B}}_{X} = (B_{i}^{2} + B_{j}^{2} + B_{k}^{2})^{1 ∕ 2}$ is the measured total magnetic field, and B_i,j,k are the orthogonal magnetic fields measured by the 3-D magnetic sensor in the IMD. Here, {i, j, k} are the orthogonal bases of the magnetic sensor (i.e., IMD), which could have an unknown orientation misalignment with respect to {x, y, z}, the orthogonal bases of the imaging system. It is important to note that the measured total magnetic field ${\hat{B}}_{X}$ remains unchanged regardless of the orientation misalignment between the implant and the imaging system. Thus, the resolution Δx of the system can be calculated as:

Δ x = \frac{Δ {\hat{B}}_{X}}{G_{X, min}},

(2)

where $Δ {\hat{B}}_{X}$ is the resolution of the magnetic sensor, G_X = dB_X/dx is the magnetic field gradient of B_X, and G_X,min is the minimum field gradient intensity. The resolution Δy and Δz can be found following the same derivation.

B. Helmholtz Coils for Magnetic Field Gradients

A Helmholtz coil produces a region with a uniform magnetic field. It consists of two identical circular coils placed facing each other along a common axis and symmetrically with respect of the center of the experimental area. They are separated by a distance (d) equal to the radius (R) of the coils. Each coil carries an equal electrical current flowing in the same direction. The generated magnetic field along the z axis at the center point can be expressed as:

B_{z} = \frac{μ_{0} n I R^{2}}{2 (R^{2} + z^{2})^{3 ∕ 2}},

(3)

where z is the coordinate axis perpendicular to the coils.

A magnetic field gradient can also be generated using two identical circular coils by setting their currents with 180° phase difference and placing them at a distance of ~ $\sqrt{3} R$ from each other. The gradient is then approximately equal to:

G_{Z} = \frac{\partial B_{z}}{\partial z} = - 0.64 \frac{μ_{0} n I}{R^{2}} .

(4)

C. Saddle Coils for Magnetic Field Gradients

We use two pairs of saddle coils to generate the other two orthogonal magnetic field gradients. A saddle coil consists of two straight coils and two arc coils. The magnetic field of the straight and arc coils along the y-axis (parallel to h as shown in Fig. 2B) can be expressed as shown in Eq. 7 and 8, respectively [9].

Fig. 2. — Saddle coil geometry: straight and arc coils.

It is important to note that both ∂B_st/∂y and ∂B_arc/∂y are constant. By calculating the gradients of B_st,y and B_arc,y, the geometry relationship of the coils can be derived. The magnetic field at the center volume can be approximated as:

B_{saddle} = μ {g_{g} \hat{x}, - 2.4398 g_{g} \hat{y}, 1.4398 g_{g} \hat{z}},

(5)

with

g_{g} = \frac{16}{3 π} {(\frac{3}{7})}^{5 ∕ 2} \times \frac{i_{g}}{{r_{g}}^{2}} \times \cos^{- 1} (1 - \frac{3}{2 a^{2}}),

(6)

where i_g and r_g are the current and radius of the saddle coil [9]. Here, a = l/d, and l, d, h, r, α₁, α₂, α₃, α₄ are shown in Fig. 2. By having two pairs of these saddle coils, the magnetic field gradient in the other two axes can be generated.

Fig. 3 shows the complete set of coils used in the proposed system: one set of Helmholtz coils to generate the magnetic field gradient in $\hat{z}$ , and two sets of saddle coils for $\hat{x}$ and $\hat{y}$ .

D. COMSOL Simulation

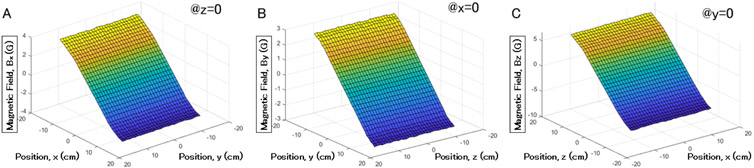
The localization system was simulated in COMSOL Multiphysics using the geometry specifications shown in Table I and a simulation volume of 28×28×28 cm³. The simulation results are shown in Fig. 4. The effective range of the gradient field is about 25×25×25 cm³. Outside this range, the linearity of the magnetic field degrades. The simulated magnetic field gradients are approximately equal to 29, 22, and 51 G/m in $\hat{x}$ , $\hat{y}$ , and $\hat{z}$ , respectively.

TABLE I.

Coil Parameters Setting

Name	Value	Description
I_saddle [A]	1.5	Current of saddle coils
r saddle [m]	0.2	Radius of saddle coils
θ1 [deg]	43.86	Start degree of saddle arc coil
θ2 [deg]	136.14	End degree of saddle arc coil
θ [deg]	46.14	Half degree of saddle coils
l [m]	1.73*r_saddle	Distance between saddle coils
a [m]	0.05*r_saddle	Thickness of insulator
n	100	Number of turns of coils
r_h [m]	0.15	Radius of Helmholtz coil
l_h [m]	1.73*r_h	Length of Helmholtz coil
I_h [A]	1	Current of Helmholtz coil

Open in a new tab

Fig. 4. — Magnetic field simulation, where (a) is the field along x-axis in the XY plane, (b) along y-axis in the YZ plane, and (c) along z-axis in the XZ plane.

In addition, thermal and heat transfer simulations were also done including the thickness of the copper wire’s insulator.

B_{st,y} = μ \frac{a d^{2} i}{4 π} [{(\frac{d^{2}}{4} + {(\frac{h}{2} - y)}^{2})}^{- 1} {(\frac{d^{2}}{4} (1 + a^{2}) + {(\frac{h}{2} - y)}^{2})}^{- \frac{1}{2}} \mp {(\frac{d^{2}}{4} + {(\frac{h}{2} + y)}^{2})}^{- 1} {(\frac{d^{2}}{4} (1 + a^{2}) + {(\frac{h}{2} + y)}^{2})}^{- \frac{1}{2}}]

(7)

B_{arc,y} = μ \frac{a d r i}{4 π} [\int_{α_{1}}^{α_{2}} \sin α {((\frac{a d}{2})^{2} + (r \cos α)^{2} + (y - r \sin α)^{2})}^{- \frac{3}{2}} d α \pm \int_{α_{3}}^{α_{4}} \sin α {((\frac{a d}{2})^{2} + (r \cos α)^{2} + (y - r \sin α)^{2})}^{- \frac{3}{2}} d α]

(8)

Our simulations showed that the coils temperature can reach 180 °C when a current of 5 A flows through them. Thus, a water cooling system will be needed in the future.

III. RFID Sensor Module

A. Sensor module

The sensor module measures the 3-D magnetic field strength and delivers the readings to a computer terminal through semi-passive UHF RFID. The module consists of a IIS2MDC magnetic sensor, Monza X-2K RFID interface with Gen2V2 protocol, microcontroller unit (MCU), and low-dropout (LDo) regulator. For the MCU, an ATTiny85 is used to establish an I2C bus between the magnetic sensor and the RFID interface for data transfer, and also manages the refresh rate of the sensor. Lastly, an AP7312 dual-rail LDO provides isolated power supply to the magnetic sensor and the rest of the components for minimized interference on the power line.

For wireless telemetry, a on-board coil antenna was designed and simulated in HFSS. The coil antenna was later verified with an network analyzer. A variable capacitor was connected in parallel with the antenna to resonate it at 915 MHz. The system-level diagram is shown in Fig. 5. The sensor module occupies an area of 20×15.25 mm². A series of 50-mil spaced pin headers are soldered for testing purposes.

Fig. 5. — System level diagram of the UHF RFID sensor module

B. Embedded program

The ATTiny85 MCU is programmed to trigger the field sensor for a measurement. Once the readings are available, the MCU transfers the data to the memory of the RFID interface chip. For low power consumption, the MCU sleep-interrupt is enabled to enter shutdown-mode between each measurement. With 0.5 Hz refresh rate and MCU clocked at 1MHz, a time-averaged current consumption of 110 μA at 3.3 V is achieved.

IV. Measurement Results

A prototype of the localization system has been developed, where each Helmholtz coil has 300 turns and each saddle coils 250 turns. Due to the high current in the coils, heat dissipation was a big concern. In this work, this current was set at 1 A. In future work, we will explore air and water cooling options to increase the magnetic field gradient of the system. We used a 3-D translational stage with 0.5 mm resolution to position the sensor probe inside of the platform. Fig. 6 shows the complete localization system and measurement setup which includes the power supplies, coil platform, RFID sensor module, 3-D translational stage, and computer.

Fig. 6. — Localization system and measurement setup.

For our experiments, we first measured the magnetic field gradient generated by the coils using a gaussmeter with 0.01 G resolution. Then, we used the RFID sensor module in a localization experiment where the module was placed in three random locations and its position was estimated using the proposed approach.

A. Magnetic Field Profile & Range

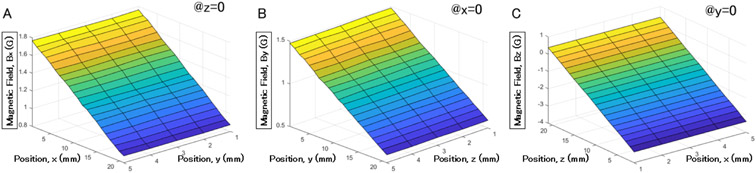
Fig. 7 shows the measured magnetic field when the gaussmeter probe was scanned through the field-of-view (FoV) by the translational stage. For each axis, we took 21×5 samples on the plane formed by that axis and an orthogonal one (e.g., for $\hat{z}$ , the plane ZX) to map the field strength spatially. The gradients in $\hat{x}$ , $\hat{y}$ , and $\hat{z}$ were measured to be 44.9 G/m, 44.5 G/m, and 187.4 G/m, respectively.

As shown in Fig. 7, the measured magnetic fields have offsets in each case. These offsets are due to the fact that the measured volume was not exactly at the center of the FoV. Since the coils generate a quasi-linear magnetic field, the origin of each measured plane was randomly chosen near the FoV center, at about 2-3 cm from the origin, to allow us to use a linear localization approach in the whole FoV. Compared to the simulated values, there is an error of ~1.8× in $\hat{x}$ and $\hat{y}$ , and ~3.5× in $\hat{z}$ . These errors come from the difference in the number of turns of the coils, the offset in the FoV, and mechanical inaccuracies during system development.

The range of the magnetic field gradient is limited by the size of the coils. In our current imaging platform, the field-of-view is about 15×15×20 cm³.

B. Localization Resolution & Error

The RFID sensor module has a IIS2MDC magnetic sensor with 1.5 mG resolution. Using Eq. 2 and the measured gradients, assuming ideal linearity and alignment, the theoretical maximum resolution is 33.4 μm, 33.7 μm, and 8 μm, in $\hat{x}$ , $\hat{y}$ , and $\hat{z}$ , respectively.

To evaluate the localization performance during normal operation, the RFID sensor module was placed at three positions inside the field-of-view. The calculated locations from the magnetic field readings were compared with the locations from the translational stage. The trajectory followed (in mm) was: A = (x₀, y₀, z₀) to B = (x₀ + 1, y₀ + 1, z₀ + 1) to C = (x₀ – 1, y₀ – 1, z₀ – 1) and back to A. The start point A was randomly chosen. The errors $e = \sqrt{Δ x^{2} + Δ y^{2} + Δ z^{2}}$ were measured to be e_A=101.7μm, e_B=78.6μm, and e_C=54.5μm, with an average error of ~80 μm.

If the system is placed in the tissue, the power delivered to the external reader will get weaker due to the attenuation, however, the accuracy of the system won’t be effect since it’s determined by the resolution of the magnetic field sensor.

V. Conclusion

In this work, we presented a magnetic field gradient-based imaging system for in-body devices capable of locating miniature implants with sub-mm resolution. The system consists of one pair of Helmholtz coils and two pairs of saddle coils which generate three orthogonal magnetic field gradients. The location of each implant is determined by applying the principle of spatial encoding through magnetic field gradients and measuring the applied magnetic field in each device. The localization resolution is independent of tissue properties and solely depends on the resolution of the implant’s magnetic sensor and the intensity of the applied gradient field. our current system generates a gradient field of up to 187.4 G/m while consuming 1 A and achieves a maximum resolution of 35 μm. A miniature RFID sensor module was developed and used in a localization experiments to validate the performance of the system, which achieved an average error of ~80 μm, which is much better compared with other works.

TABLE II.

Performance Comparison

Metric	[10]	[11]	[12]	This work
Translational and Ang. Dimension	3, 0	3, 2	3, 0	3, 0
Number of Sensors	1	8×8	4^#	1
Resolution (mm)	0.1	2.1	-	0.035
Error^* (mm)	0.3^†	0.8	2.8	0.102^††
Field of View (cm)	20×20×10	7×7×5	24×30×8	15×15×20
Method	Magnetic gradient	Static field	Optical& ultrasound	Magnetic gradient

Open in a new tab

Excluding ultrasound machine

Max. single location error

^†

Averaging of 5 samples

^††

Averaging of 4 samples

Acknowledgements

The authors would like to thank the funding support of USC and NIH/NIBIB under award number R21EB030244.

References

[1].Meng E et al. “Insight: implantable medical devices”. In: Lab on a Chip 14.17 (2014), pp. 3233–3240. [DOI] [PubMed] [Google Scholar]
[2].Khan S et al. “Wireless power transfer techniques for implantable medical devices: A review”. In: Sensors 20.12 (2020), p. 3487. [DOI] [PMC free article] [PubMed] [Google Scholar]
[3].Pahlavan K et al. “RF Localization for Wireless Video Capsule Endoscopy”. In: Int J Wireless Inf Networks 19.4 (2012), pp. 326–340. [Google Scholar]
[4].Khan U et al. “Comparison of TOA and RSS based techniques for RF localization inside human tissue”. In: 2011 IEEE EMBC. Aug. 2011, pp. 5602–5607. [DOI] [PubMed] [Google Scholar]
[5].Werber D et al. “Investigation of RF transmission properties of human tissues”. In: Adv. in Radio Science Kleinheubacher Berichte; 2005. Vol. 4. 2006, pp. 357–360. [Google Scholar]
[6].Wang Max L. et al. “Ultrasonic Implant Localization for Wireless Power Transfer: Active Uplink and Harmonic Backscatter”. In: 2019 IEEE Int. US Symp. (IUS) Oct. 2019, pp. 818–821. [PMC free article] [PubMed] [Google Scholar]
[7].Herment A et al. “Limitations of ultrasound imaging and image restoration”. In: Ultrasonics 25.5 (Sept. 1987), pp. 267–273. [DOI] [PubMed] [Google Scholar]
[8].Monge M et al. “Localization of microscale devices in vivo using addressable transmitters operated as magnetic spins”. In: Nature Biomedical Engineering 1.9 (2017), pp. 736–744. [DOI] [PubMed] [Google Scholar]
[9].Jeon S et al. “Magnetic navigation system with gradient and uniform saddle coils for the wireless manipulation of micro-robots in human blood vessels”. In: IEEE Trans. on Mag 46.6 (2010), pp. 1943–1946. [Google Scholar]
[10].Sharma Saransh et al. “Wireless 3D Surgical Navigation and Tracking System with 100um Accuracy Using Magnetic-Field Gradient-Based Localization”. In: IEEE Trans Med Imaging PP (Apr. 5, 2021). [DOI] [PubMed] [Google Scholar]
[11].Son D et al. “A 5-D Localization Method for a Magnetically Manipulated Untethered Robot Using a 2-D Array of Hall-Effect Sensors”. In: IEEE/ASME Trans. on Mechatronics 21.2 (2016), pp. 708–716. [DOI] [PMC free article] [PubMed] [Google Scholar]
[12].Parent F et al. “Intra-arterial image guidance with optical frequency domain reflectometry shape sensing”. In: IEEE Trans. on Medical Imaging 38.2 (2018), pp. 482–492. [DOI] [PubMed] [Google Scholar]

[R1] [1].Meng E et al. “Insight: implantable medical devices”. In: Lab on a Chip 14.17 (2014), pp. 3233–3240. [DOI] [PubMed] [Google Scholar]

[R2] [2].Khan S et al. “Wireless power transfer techniques for implantable medical devices: A review”. In: Sensors 20.12 (2020), p. 3487. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R3] [3].Pahlavan K et al. “RF Localization for Wireless Video Capsule Endoscopy”. In: Int J Wireless Inf Networks 19.4 (2012), pp. 326–340. [Google Scholar]

[R4] [4].Khan U et al. “Comparison of TOA and RSS based techniques for RF localization inside human tissue”. In: 2011 IEEE EMBC. Aug. 2011, pp. 5602–5607. [DOI] [PubMed] [Google Scholar]

[R5] [5].Werber D et al. “Investigation of RF transmission properties of human tissues”. In: Adv. in Radio Science Kleinheubacher Berichte; 2005. Vol. 4. 2006, pp. 357–360. [Google Scholar]

[R6] [6].Wang Max L. et al. “Ultrasonic Implant Localization for Wireless Power Transfer: Active Uplink and Harmonic Backscatter”. In: 2019 IEEE Int. US Symp. (IUS) Oct. 2019, pp. 818–821. [PMC free article] [PubMed] [Google Scholar]

[R7] [7].Herment A et al. “Limitations of ultrasound imaging and image restoration”. In: Ultrasonics 25.5 (Sept. 1987), pp. 267–273. [DOI] [PubMed] [Google Scholar]

[R8] [8].Monge M et al. “Localization of microscale devices in vivo using addressable transmitters operated as magnetic spins”. In: Nature Biomedical Engineering 1.9 (2017), pp. 736–744. [DOI] [PubMed] [Google Scholar]

[R9] [9].Jeon S et al. “Magnetic navigation system with gradient and uniform saddle coils for the wireless manipulation of micro-robots in human blood vessels”. In: IEEE Trans. on Mag 46.6 (2010), pp. 1943–1946. [Google Scholar]

[R10] [10].Sharma Saransh et al. “Wireless 3D Surgical Navigation and Tracking System with 100um Accuracy Using Magnetic-Field Gradient-Based Localization”. In: IEEE Trans Med Imaging PP (Apr. 5, 2021). [DOI] [PubMed] [Google Scholar]

[R11] [11].Son D et al. “A 5-D Localization Method for a Magnetically Manipulated Untethered Robot Using a 2-D Array of Hall-Effect Sensors”. In: IEEE/ASME Trans. on Mechatronics 21.2 (2016), pp. 708–716. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R12] [12].Parent F et al. “Intra-arterial image guidance with optical frequency domain reflectometry shape sensing”. In: IEEE Trans. on Medical Imaging 38.2 (2018), pp. 482–492. [DOI] [PubMed] [Google Scholar]

PERMALINK

Towards Magnetic Field Gradient-Based Imaging and Control of In-Body Devices

Hongxiang Gao

Yubin Lin

Manuel Monge

Abstract

I. Introduction

Fig. 1.