REGIONAL GRADIENT STRATEGIC SENSORS CHARACTERIZATIONS

ISSN 2347-1921 REGIONAL GRADIENT STRATEGIC SENSORS CHARACTERIZATIONS Raheam A. Al-Saphory1*, Naseif J. Al-Jawari2 and Assma N. Al-Janabi2 1 Department of Mathematics, College of Education for Pure Sciences, Tikrit University, Tikrit, IRAQ. 1 Email: saphory@hotmail.com 2 Department of Mathematics, College of Science, Al-Mustansiriyah University, Baghdad, IRAQ. 2 njaljawari@hotmail.com asm_no_2006@yahoo.com 2 ABSTRACT In the present paper, the characterizations of regional gradient strategic sensors notions have been given for different cases of regional gradient observability. The results obtained are applied to two dimensional linear infinite distributed system in Hilbert space where the dynamic is governed by strongly continuous semi-group. Various cases of regional strategic sensors are considered and analyzed in connection with regional gradient strategic sensors concepts. Also, we show that there is a various sensors which are not gradient strategic in usual sense for the considered systems, but may be regionally gradient strategic of this system. Keywords: -strategic sensors; exactly -observability; weakly -observability; diffusion systems. Academic Discipline And Sub-Disciplines: Applied Mathematics/ Control Systems and Analysis 2010 AMS SUBJECT CLASSIFICATION: 93A30; 93B07; 93B28; 93C05; 93C28. TYPE (METHOD/APPROACH) Mathematical approach for parabolic distributed parameter systems gvorned by semi-group operator in a Hilbert state space. Council for Innovative Research Peer Review Research Publishing System Journal: JOURNAL OF ADVANCES IN MATHEMATICS Vol . 10, No. 6 www.cirjam.com , editorjam@gmail.com 3605 | P a g e May 25, 2015 ISSN 2347-1921 1. NTRODUCTION The analysis of distributed parameter systems refers to a set of concepts such as controllability, observability, detectability [13-14, 18]. The study of these concepts can be made via actuators and sensors structures see [14-17], these concepts give an important link between a system and it’s environment [15-18], so that the concepts of actuators and strategic sensors for a class of distributed parameter systems are introduced in order that controllability and observability can be achieved [14-18]. The regional analysis is one of the most important notion of system theory [20-22], it consist to reconstruction the state observation on a sub-region of spatial domain Ω in finite time [19-23, 25-28], this concepts introduced and developed by El-Jai et al. An important extended to the asymptotic case for infinite time by El-Jai and AlSaphory in several works [1-7]. The study of regional gradient observability for a diffusion system has been given in [2728] where one is interested in knowledge of the state gradient only in a critical sub-region of the system domain without the knowledge of the state itself. Moreover, the applications are motivated by many real world see [10-12, 22]. Commercial buildings are responsible for a significant fraction of the energy consumption and greenhouse gas emissions in the U.S. and worldwide. Consequently, the design, optimization and control of energy efficient buildings can have a tremendous impact on energy cost and greenhouse gas emission. Mathematically, building models are complex, multi-scale, multiphysics, highly uncertain dynamical systems with wide varieties of disturbances [10]. 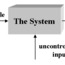Fig. 1: Room control model with sensor, in flow and out flow In this paper we use a model problem to illustrate that distributed parameter control based on PDEs, combined with high performance computing can be used to provide practical insight into important issues such as optimal sensor/actuator placement (may be best or strategic sensors/ actuators) and optimal supervisory building control. In order to illustrate some of the ideas, we consider the problem illustrated by a single room shown in (Figure 1). This model one can reformulated [11] as spatial case of more general model of distributed parameter systems and represented in the next section (see Figure 2). In addition, the characterization of regional strategic sensors have been given for various types of regional observability in [7]. The purpose of this paper is to extended these results in [7] to the case of regional gradient sensors. Thus, we give a characterization of regional gradient strategic sensors for different cases of regional gradient observation. Therefore, we study and analyze the relationship between the regional gradient strategic sensors and the regional exactly gradient observability. So, the outline of this paper is organized as follows: Section 2 is present problem statement and basic definitions with characterization of the regional gradient observability. The mathematical concepts of regional gradient strategic sensors in a various situations are studied and developed in section 3. In the last section we gives an application about different sensors locations. 2. REIONAL GRADIENT OBSERVABILITY In this section, we are interested to recall the notion of regional gradient observability and give original results related to particular systems as in [27-28]. 2.1 Problem Statement Let Ω be a regular bounded open subset of , with a smooth boundary Ω and be a non-empty given sub-region of Ω. Let 0, , > 0 be a time of measurement interval. We denoted = Ω × 0, and � = Ω ×]0, T[. Consider the following distributed parabolic defined by �, �, = �, 0 = �, = 0 + in � 0 in Ω in � (1) with the measurements given by the output function We have ∙, = = , , =1 ( 3606 | P a g e (2) ), with �( ). May 25, 2015 ISSN 2347-1921 Suppose that - is elliptic, i.e., there exists �� , =1 =1 � 2 > 0 such that , almost everywhere (a.e) on , ∀� = �1 , … , � . This operator is a second order linear differential operator, which generator a strongly continuous semi-group 1 0 on the Hilbert space = (Ω) and is self-adjoint with compact resolvent. The operator , and , , depend on the structure of actuators and sensors [18]. The space , and � be separable Hilbert spaces where is the state space, = 2 0, , is the control space and � = 2 0, , is the observation space where and are the numbers of actuators and sensors (see Figure 2). Fig. 2: The domain of �, the sub-region �, various sensors locations Under the given assumption, the system (1) has a unique solution [24]: �, = 0 � + ( − �) 0 � � (3) The problem is to provide sufficient conditions to ensure that, how to extend the results in [7], so that to give a sufficient conditions of regional gradient strategic sensors which achieve the observability in sub-region using various regional gradient sensors. 2.2 Definitions And Characterizations The regional gradient observability concept and reconstruction gradient state have been introduced by Zerrik E. et al. as in ref.s [27-28] and recently this concept is developed to the regional asymptotic case by Al-Saphory R [1-7]. Consider the autonomous system to (1) given by �, �, = in �, 0 = 0 � �, = 0 (4) in Ω in � The solution of (4) is given by the following form, �, = 0 � , ∀ (5) 0, The measurements are obtained through the output function ., �, = We first recall a sensors is defined by any couple (D, f ), where D is spatial support represented by a nonempty part of Ω and f represents the distribution of the sensing measurements on D. Depending on the nature of D and f, we could have various type of sensors. A sensor may be pointwise if D = {b} with Ω and = (. − ), where is the Dirac mass concentrated at b. In this case the operator C is unbounded and the output function (2) can be written in the form [13-14] = ( , ) It may be zonal when �, = ⊂ Ω and 2( ). The output function (2) can be written in the form � Now, we define the operator → : = Thus, we get that ∙, = 3607 | P a g e . � (6) (∙ ,0) May 25, 2015 ISSN 2347-1921 where K is bounded linear operator [8]. :� → We note that = is the adjoint operator of K defined by (7) 0 Consider the operator 1 : → It's adjoint → ( 2 ( Ω)) =( �1 ,…, is given by � (8) ) Ω)) → 1 (Ω) → = is a solution of the Dirichlet problem : where Ω ( 2( ∆ = −div =0 in Ω in Ω For a nonempty subset : and (9) of Ω, we consider the operators ( 2 ( Ω)) → ( 2 ( )) → = ∣ ( Ω) → 2 ( ) → = ∣ ∣ is the restriction of (10) 2 (11) : where [9]. ⋄ Their adjoints are respectively denoted by ( 2 ( )) : → and = )→ → and are defined by ( 2 ( Ω)) ∣ in 0 in Ω (12) Ω) (13) The ∣ in → = 0 in Ω idea of gradient observability is based on the existence of an operator : � → ( 2 ( )) such that = 0 . This is a natural extension of the observability concept [8]. Then we defined the operator = from � into ( 2 ( )) as in [27]. Now, let us denoted the system (4) together with the output (2) by (4)-(2). 2( : 2( Definition 2.1: The system (4)-(2) is said to be regionally exactly observable on a sub-region (exactly - observable), if = 2 ( ) Definition 2.2: The system (4)-(2) is said to be regionally weakly observable on (. ) = 2( (weakly - observable), if ) Definition 2.3: The system (4)-(2) is said to be regionally exactly gradient observable on (exactly - observable), if = ( 2 ( )) Definition 2.4: The system (4)-(2) is said to be regionally weakly gradient observable on (weakly - observable), if (. ) = ( 2 ( )) We see that if a system is weakly gradient, viz., if – observable then there is one to one relationship between the output and the initial is given and 0 satisfies = . 0 , then 0 is a unique. Remark 2.5: We can deduced that, the definition 2.4 is equivalent to say that the system (4)-(2) is weakly observable, if 3608 | P a g e May 25, 2015 - ISSN 2347-1921 = {0} Then, the following characterization can extend to the regional gradient case as in ref. [26]. Proposition 2.6: The system (4)-(2) is exactly -observable if and only if there exist > 0 such that for all ( 2 ( )) , such that, (14) � ( 2 ( )) Proof: The proof of this property is deduced from the usual results on observability considering , be a reflexive Banach space and let and , , , ⊂ . There exist > 0 such that 1. 2. [13]. Let , then the following conditions are equivalent ∀ Now, by applying the above result we obtain the equivalent condition for exactly Let = �, = ( 2 ( )) , = = Now, since the system is exactly such that 2( 2( ( and )) . = -observable we have ∀ )) Remark 2.7: We have: -observable as: .□ ⊂ , which is equivalent to that fact there exist > 0, (1) The regional state reconstruction will be more precise than the whole domain if we estimate the state in the whole the domain. (2) From (14) there exists a reconstruction error operator that gives the estimation If we put e = 0 − 0 , we have e e ( 2 ( )) ⟹ Where − 0 0 0 ( 2( 0 )) − 0 ( Proof: Since the system is exactly since ( 2 0 ( 2 (Ω)) 2 ={ = 0 ( 0: 0 2 To prove > 0 and 0 = 2( 2( 0 )) < ∞}, 0 ( 2 ( )) , and then, -observable then it is exactly < ∞, 0 = 2 0, ,� ), ∀ 0 � 0 2 > 0 such that ∀ -observable. 0 2 ( ), we have ( ), where (15) ∀ = 1,2, … . then from (15) and since a system exactly -observable, then there exist 1 > 0 such that = in is the estimated state of the system. , ∀ >0 0, ,� 2 : 0 -observable there exist , then and then ( 2 ( )) = 2 0 ) )) ⊂ 0 2 (Ω)) is the exact state of the system and 2( of the initial state ( 2 (Ω)) Proposition 2.8: If the system is exactly 0 2( 0 = . By choosing 0 � (16) 0 � Then, we can get 0 ( 2 ( )) 0 (17) 0 � 2 And by substituting (16) in (17), we obtain 0 ( 2 ( )) 0 � Therefore this system is exactly 3609 | P a g e -observable with = 1. May 25, 2015 ISSN 2347-1921 Remark 2.9: From the above proposition we can get the following result: If the system is exactly 1 -observable then it is exactly G-observable in 1 for all 3. REGIONAL GRADIENT STRATEGIC SENSORS ⊂ (exactly 1 -observable). The purpose of this section is to give the characterization for sensors in order that the system (4)-(2) which is observable in . 3.1 �� -Strategic Sensors Definition 3.1: A sensor ( , ) is regional gradient strategic on ( -strategic) if the observed system is weakly - observable. Definition 3.2: A sensor ( , )1 is -strategic if there exist at least one sensor ( 1, 1 ) which -strategic. We can deduce that the following result: Corollary 3.3: A sensor is -strategic if the observed system is exactly Proof: Let the system exactly -observable. -observable, then , we have = ( 2 ( )) From decomposition sub-space of direct sum in Hilbert space, we represent ( 2 ( Ω)) by the unique form [13] = ( 2 ( Ω)) + We obtain = {0} This is equivalent to [9] (. ) = ( 2 ( )) Finally, we can deduce this system is weakly Corollary 3.4: A sensor is Proof: Since a sensor is - observable and therefore this sensor is -strategic if and only if the operator � = -strategic.□ is positive definite. -strategic this mean that the system is weakly - observable, ( 2 ( )) such that let <� , >( 2( )) and therefore = 0 then ( 2 ( )) such that = 0, then < , >� = 0 and thus, Hence , =0 = 0, i.e., � is positive definite. , thus, Conversely, let <� � >( 2( )) =0 = 0 thus the system is weakly - observable and therefore a sensor is -strategic.□ Remark 3.5: From the previous results, we obtain that: (1) If the system is exactly strategic. -observable then the system is weakly (2) A sensor which is regional gradient strategic sensor in gradient strategic sensor in 2 ( 2 -strategic) for any 2 ⊂ 1 . (3) The concept of exact 1 ( 1 -observable and therefore this sensor is -strategic) for a system where -observability is more restrictive than weak 1 - ⊂ Ω, is regional -observability. Now, assume that the operator has a complete set of eigenfunction in 1 Ω , denoted by , which is orthonormal in 2 ( ) and the associated with the eigenvalue � of multiplicities , then the concept of regional gradient strategic on can be characterized by the following result: Theorem 3.6: Assume that sup 3610 | P a g e = < ∞, then the suite of sensors ( , )1 , -strategic if May 25, 2015 ISSN 2347-1921 (1) (2) ∀ = Where =( ( ) 1, for 1 =1 ) = =1 , and ,1 in the pointwise case ( ) � < > , � in the zonal case 2 Proof: We will discussed the case where the sensors are of pointwise type and located inside the domain Ω. The suite of sensors ( , )1 is -strategicif and only if ( 2 ( )) < , >( 2( = 0, ∀ )) Suppose that the suite of sensors ( , =( < 1 0, 2 > < Let , 0 2( ,…, )= 0, = =1 < , >( 0 )= ≠ , 0 )) = 0 2( 2( x -strategicbut for a certain �,  , then there exists a vector  0. So, we can construct a nonzero 0 2( ) considering . ,1 = ( 0, =1 < 0 , … , 0 ), � =1 < � then , 0 ( > 2( ), ) 0 > 2 Ω is the solution of the following system: �, �, = �, 0 = 0 �, = 0 + − =1 in �, =− �, 0 = �, = 0 Multiply (18) by � �, =1 � 0 �, (18) in Ω in � Consider the system: Q = 0. and = where is )1 ≠ 0, such that ) > � ⟹ in (19) in Ω in � and integrate on Q, we obtain �, � ( − )  � �, �, � �, � � + . But we have � �, �, �  Ω � �,  then: Ω � �, �, �  integrating by parts we obtain 3611 | P a g e � + Ω �, �, � �, =1 � + 0 �, �, �+ �+ ( − ) �, � � �, �, �, � � � �, ℥ �, �, � � May 25, 2015 Ω � � � �, �, � − �, ƞ ƞ, the boundary conditions give Thus Ω �, � �, Ω � �, �, � and we have < , 0 2( (ƞ, ) ƞ � )) = �, Then −� ( − ) ∞ =1 = = , =1 � < =1 ∞ =1 −� ( − ) = ∞ =1 � �, > =1 − < ( �, � . 2( � ( − ) . , =1 � =1 0 °, � � ( − ) �, � =− But ( − ) �, � , � =1 Ω ƞ =1 ( − ) =1 0 ƞ, � + =1 �=− >( ISSN 2347-1921 , ) 0, > 2( ) =1 � ) therefore < , 0 >( 2( )) Thus < , 0 This is true for all strategic.□ >(  2( 2 )) =− =− (0, ; =1 0 =1 0 ), then ∞ =1 � 0 − � − ( ( ) ) ( − ) − (20) =0 which contradicts the assumption that the suite of sensors is - We can deduced the following result: Corollary 3.7: In the one dimension case, a sensor is ,∀ 1, where -strategic if and only if = and = is given in theorem 3.6. Remark 3.8: From the previous results, we can get (1) The Theorem 3.6 implies that the required number of sensors is greater than or equal to the largest multiplicity of the eigenvalues. (2) By infinitesimally deforming the domain, the multiplicity can be reduced to one [19]. Consequently, -strategic sensors can be achieved using only one sensor. Now, we can deduced that various sensors which are not strategic in usual sense for systems, but may be strategic and achieve the -observability. This is illustrated in the following counter- example. - 3.2 A Counter- Example Consider the system described by the parabolic equation �, 2 = 0,1 = � ,0 = �2 �, 1, 0 � in ]0,1 × 0, [ =0 in ]0, [ in ]0,1[ Suppose that the measurement is given by pointwise sensor located in function 3612 | P a g e (21) ]0,1[ which is given by the following output May 25, 2015 ISSN 2347-1921 ., = (22) �, Ω �− �= , , (0, ) Where = 2 sin �� and � = − 2 � 2 . First, we must prove that the system (21)-(22) is not weakly observable in Ω, that means the sensors ( , ) is not strategic. For this purpose, we can write the system (21) as a state space one dimensional system �, Where �, = � ,0 = 2 = �2 0 � 0 generate the continuous semigroup ( ∞ =1 = � < 0, > ∞ =1 = � < 0, > 2�2 given by [17]. 2 are the eigenfunctions associated with the eigenvalues of = Ω = ( ) 0 The system (21)-(22) is weakly observable if . Then from solution 0 = {0}. then system (21)-(22) is not weakly observable on Ω=(0,1) and a sensor ( , ) is not strategic. As proved in [27], if A sensor is 0 2 (Ω ) Where, = 2 sin �� , � = − of (21), we have �, ) ⇔ : -strategic on (0,1) ∞ =1 = [1, − 1] ∩ � . Since sin � =0⇔ = condition in ⟹ = . 2 +1 ∞ =1 2 Consequently, the system is weakly observable on (0,1). And then, it is G-strategic on (0,1) ⇔ = [0, − ∩�. Since cos � = ⇔ =2 +12⟹ =2 +12 . Consequently, the system is weakly G-observable on (0,1).□ Corollary 3.9: If the (3.6) is satisfied and a sensor is system (21)-(22) -strategic. is exactly -observable, rank Now, assume that a sensor is not gradient strategic in whole the domain Ω and let ( ) ⊂ � be such that = {( ) } and = � \ . � be a basis in ( Proposition 3.10: The following properties are equivalent: 1. 2. 3. A sensor is -strategic. ) {( ) }=( 2 2 If ( ) is such that < , 4. If = 0 in Ω\ , then Proof: 1⟹2 Since sensors are Let 2 ( − = = − < � ( 2 >( 2 we deduced that ) 3⟹4 Let 3613 | P a g e < ) 2 Ω ) ) = , then Ω ) . Let = 0. . < , . Then 2 ) >0∃ ( ( ) . For any ( 2 >� >� . } 2 − 2 >( < , { 2⟹3 Let 2 ( , = 0 for all ) 2 -observable. � such that , but ) < , and hence < , 2 ( 2 -strategic this mean that the system is weakly >0∃ ) . Then for >( = 0 for all theorem >� , and thus < ) such that < , with = 0, ∀ . Thus, = 0. = 0 in Ω\ . May 25, 2015 ISSN 2347-1921 Now Consider < , Since >( = 2 ) ). For ( = < , >( , we have = 0, we get = 0 in Ω and 4⟹1 Consider 2 ( = 0, ∀ 2 ( then < , >( I. ) such that = 0. We have = = 0. Ω ) 2 � < , 2 Ω ) >( 2 = ) {( ) ) ( < , >( . Hence = 0.□ 2 ) = 0. Therefore, ) } and then < , >( 2 = 0, ∀ ) Therefore = < , >( 2 . = 0 in Ω\ . ) From the assumption we have < , >( 2 = 0, ∀ ) We can deduced the following result: Corollary 3.11: ⊂ Ω such that < Under the hypotheses of , ≠ . >( 2 ) = 0, ∀ , , Proposition 3.10, a = 0, ∀ < , Since 0 . Let = Ω ) =< >( 2 and in , 0 >( 2 I. Then 0 Ω ) = 2 ) < , 0 >( = 0 in Ω\ , under the assumption of Corollary 3.11 we have = < From (23)-(24), we obtain = 0 ,∀ < , 0 >( 2 Ω ) , 0 >( = 2 0 ( 0 2 2 Ω ) is -strategic in all = 0 in Ω\ . Then we only need to show Proof: To deduce the result from previous Proposition 3.10, we take that sensors = 0 ) (23) (24) . 4. APPLICATION TO SENSORS LOCATIONS In this section, we give specific results related to the different case presented in the above section. First we consider internal sensors (zonal, pointwise, filament in rectangular and disk domain) the presented result give information on the structure of . Consider the system �1 , �2 , = ∆ �1 , �2 , in , in Ω, �1 , �2 , 0 = 0 �1 , �2 �1 , �2 , = 0 in � Let Ω = (0,1) × (0,1) and let = ( 1 , 1 ) × ( 2 , eigenvalue of the system (25) are given by: 2 �1 , �2 = 1− 1 Associated with eigenvalue � =− sin � (�1 − 1) 1− 1 2) � be the considered region is subset of Ω, the eigenfunctions and the (�2 − 2) 2− 2 2 2 1− 2− 2 (25) 1 2 + 2− 2 (26) (27) 2 4.1 Internal Zone Sensor Consider the system (25) together with output function (2) where the sensor supports can by written by the form = 3614 | P a g e �1 , �2 , �1 , �2 �1 �2 are located in Ω. The output (2) (28) May 25, 2015 ISSN 2347-1921 Where ⊂ Ω is location of zone sensor and eigenvalues (26) and (27). 2( ). In this case of (see Figure 3), the eigenfunctions and the Fig. 3: Domain Ω, sub-region � and location � of internal zone sensor However , if we suppose that 1− 1 2− 2 2 2 Then multiplicity of � is = 1 and then one sensor ( , ) my be sufficient to achieve and (28) [19]. Let the measurement support is rectangular with = [�01 − 1 , �01 + 1 ] × [�02 − 2 , �02 + 2 ] Ω Then, we have the following result Corollary 4.1: If 1 strategic if (�01 − 1) 1− 1 and (�02 − 1) 2− 2 -observable of the systems (25) is symmetric about �1 = �01 and 2 is symmetric about �2 = �02 , then the sensor , is - � for some , . 4.2 Internal Pointwise Sensor In this case the out put function is given by: = With If =( 1 , 1− 1 2− 2 2) �1 , �2 , �1 − 1− 1) 1− 1 , then and − 2 �1 �2 (29) is location of pointwise sensor as defined in (see Figure 4) Fig. 4: Rectangular domain, and location � of internal pointwise sensor = 1 and one sensor ( , Corollary 4.2: The sensor ( 1 , �2 ( 2− 2) 2− 2 , is ) may be sufficient for -observability of the systems (25)-(29) -strategic if �, for some , . 4.3 Internal Filament Sensor Consider the case where the observation is given on the curve � = 3615 | P a g e with 1 (0,1) (see Figure 5) May 25, 2015 ISSN 2347-1921 Fig. 5: Rectangular domain, and location � of internal filament sensors Corollary 4.3: If the measurements recovered by filament sensor (�, � ) such that is symmetric with respect to the line � = �0 . Then the sensor (�, (�01 − 1) 1− 1 and (�02 − 2) 2− 2 �) is -strategic if �, for , = 1, … , . Remark 4.4: These results can be extended to the following: 1. Case of Neumann or mixed boundary conditions [4-5]. 2. Case of disc domain   ( D,1) 3. Case of boundary sensors where and   (0, r ) where   and 0  r  1 C  L( X , R q ) , we refer to see [13-14]. [1-3] . 4. We can show that the observation error decreases when the number and support of sensors increases [23, 25]. 5. CONCLUSION We have been introduced a sufficient condition of regional gradient strategic sensors in order to achieves regional gradient observability. Many interesting results concerning the choice of sensors structure are given and illustrated in specific situations. Various questions still opened under consideration. For example, these result can be extended to the boundary case with parabolic and hyperbolic systems [8]. ACKNOWLEDGMENTS Our thanks in advance to the editors and experts for considering this paper to publish in this estimated journal and for their efforts. REFERENCES [1] Al-Saphory, R. and El Jai, A. 2001. Sensor structures and regional detectability of parabolic distributes systems. International Journal of Sensors and Actuators. Vol. 90.163-171. [2] Al-Saphory, R. and El Jai, A. 2001. Sensors characterizations for regional boundary detectability in distributed parameter systems. International Journal of Sensors and Actuators. Vol. 94.1-10. [3] Al-Saphory, R. and El Jai A. 2002. Regional asymptotic state reconstruction. International Journal of Systems Science. Vol. 33. 1025-1037. [4] Al-Saphory, R. 2010. Strategic sensors and regional exponential observation in Neumann boundary conditions. Zanco Journal of Pure and Applied Science. Vol. 22, 1-11. [5] Al-Saphory, R., Al-Jawari, N. and Al-Qaisi, A . 2010. Regional gradient detectability for infinite dimensional systems. Tikrit Journal of Pure Science. Vol. 15, No. 2. 1-6. [6] Al-Saphory, R. 2011. Strategic sensors and regional exponential observability. ISRN Applied Mathematics. Vol. 2011. Article ID 673052. pp. 1-13. [7] Al-Saphory, R., Al-Joubory, M. and Jasim, M. 2013. Regional strategic sensors characterizations. Journal of Mathematical and Computational Science. 3, 401-418. [8] Boutoulout, A., Bourray, H. and Khazari, A. 2014. Flux observability for hyperbolic systems. Applied Mathematics and Information Sciences Letters. Vol. 2 , No. 1, 13-24. 3616 | P a g e May 25, 2015 ISSN 2347-1921 [9] Brezis, H. 1987. Analyse fonctionnalle; Theorie et applications. 2em tirage. Masson. Paris, France. [10] Burns, J., Jorggaard, J., Cliff, M. and Zietsman, L. 2009. A PDE approach to optimization and control of high performance buildings, Workshop in Numerical Techniques for Optimization Problems with PDE Constraints, No. 04/2009, DOI: 10.4171/OWR/2009/04. 25-31 January. Houston, Denmark. [11] Burns, J., Jorggaard, J., Cliff, M. and Zietsman, L. 2010. Optimal sensor design for estimation and optimization of PDE Systems, 2010 American Control Conference. Marriott Waterfront, Baltimore, MD, USA. June 30-July 02, 2010. [12] Chen Y., Moore K., and Song, Z. 2004. Diffusion boundary determination and zone control via, mobile actuatorssensors networks (MAS-net)-challenge and opportunities. SCOIS. Utah state university, Logan, UT84322, USA. [13] Curtain, R. F. and Pritchard, A. J. 1978. Infinite dimensional linear theory systems; Lecture Note in Control and Information Sciences. Spring – Verlag, New York. [14] Curtain, R. F. and Zwart, H. 1995. An introduction to infinite dimensional linear system theory. Springer-Verlag, New York. [15] El Jai, A. and Pritchard, A. j. 1987. Sensors and actuators in distributed system. International Journal of Control. Vol. 46, 1139-1153. [16] El Jai, A. and Amouroux, M. 1988. Sensors and observers in distributed parameter systems. International Journal of Control. Vol. 47, 333-347. [17] El Jai, A. 1991. Distributed systems analysis via sensors and actuators, International Journal of Sensors and Actuators.Vol. 29, 1-11. [18] El Jai, A.. and Pritchard A. j. 1988. Sensors and controls in analysis of distributed system, Ellis Harwood series in Mathematics and Applications, Wiley, New York. [19] El Jai, A. and El Yacoubi, S. 1993. On the number of actuators in a parabolic system, Applied Mathematics and Computer Science. Vol.3, No.4, 139-150. [20] El Jai, A., Simon, M.C. and Zerrik, E. 1993. Regional observability and sensor structures, International Journal of Sensor and Actuator. Vol. 39, No. 2, 95-102. [21] El Jai, A., Amouroux, M. and Zerrik, E. 1994. Regional observability of distributed systems. International Journal of Systems Science. 1994, Vol. 25, No.2, 301-313. [22] El Jai, A., Simon, M.C., Zerrik, E. and Amouroux, M. 1995. Regional observability of a thermal proces. IEEE Transaction on Automatic Control. Vol. 40, 518-521. [23] El Jai A. and Hamzauoi, H. 2009, Regional observation and sensors. International Journal of Applied Mathematics and Computer Sciences. Vol. 19, No. 1, 5-14. [24] Gressang, R. and Lamont, G.1975. Observers for systems characterized by semi-group. IEEE on Automatic and Control. 20, 523-528. [25] Hamzauoi, H., 2008, On choice of actuators-sensors structures in the systems, Ph. D. Thesis, Perpignan, France. [26] Zerrik, E. 1993. Regional analysis of distributed parameter systems, Ph.D. Thesis. University of Rabat, Morocco. [27] Zerrik, E., Bourray H. and Badraoui L. 2000. How to reconstruct a gradient for parabolic systems. Conference of MTNS 2000. Perignan, France, June-2000, 19-23. [28] Zerrik, E. and Bourray, H. 2003. Gradient observability for diffusion systems. International Journal of Applied Mathematics and Computer Sciences. Vol. 2, 139-150. 3617 | P a g e May 25, 2015 ISSN 2347-1921 Author’s Biographies: Raheam Al-Saphory is professor associated at the TIKRIT University in IRAQ. He received his Ph.D. degree in Control System and Analysis in (2001) from LTS/ Perpignan University France. He has a post doctorate as a researcher in 2001-2002 at LTS. Al-Saphory wrote one book and many papers in the area of systems analysis and control. Also he is a supervisor of many Ph D. and Msc. students and he was Ex-head of Departement of Mathematics /College of Eduction for Pure Science Tikrit University 20102011. He visite many centres and Scientific Departments of Bangor University/ Wales/ UK with academic staff of Iraqi Universities in 2013. He is a coordinator of postgraduate studies at Department of Mathematics 2014present. Naseif Al-Jawari is assistant Proffessor at the Al-Mustansiriyah University, IRAQ. He received his Ph.D. degree in Optimal Control Theory in (2000) from Faculty of Mathematics/ Łódź University Poland. Al-Jawari wrote many papers in the area of systems analysis and Optimization. Also he is a supervisor of many Ph D. and Msc. students. He is head of Applied Mathematics Branch/ Department of Mathematics/ College of Science/ Al-Mustansiriyah University 2012present. Assma N Al-Janabi is an instructor and researcher at the Department of Mathematics/ College Science/ Al-Mustansiriyah University/ IRAQ 2012Present. Here research area focused on Distributed Parameter Systems Analysis and Control. She is obtained here Ms.c. degree from Al-Nahrain University in (2003). 3618 | P a g e May 25, 2015