感染症数理モデルとCOVID-19

はじめに

今回の新型コロナ流行（COVID-19）は、感染の規模とスピードからすれば、100 年前のスペイン・インフルエンザに比肩しうるパンデミックであるが、100 年前との大きな違いは、科学的な対抗策の進歩である。スペイン・インフルエンザ流行当時においては、「感染」による流行という事実がわかっていても、感染因子の特定も困難であり、ワクチン開発などは全くできなかったのであるから、今日までの医学的対処法の著しい進歩はいうまでもない。

一方、ワクチンが開発されない段階では、非薬剤的な流行制御がおこなわれることになるが、その点においても当時は感染ダイナミクスを記述する理論がなかったから、集団レベルでの対応策を考えることができなかった。そこに現れた革新的アイディアが感染症数理モデルである。以下では感染症数理モデルが今回のCOVID-19 において果たしている、あるいは果たすべき、役割を理解するために、まずその歴史を紹介し、その後今回のCOVID-19 への適用において現れた若干の問題を論じたい[1]。数理モデルそのものに関しては、簡単な紹介を本稿の付録とした。詳しくは[2] [3] [4] 等を参照していただきたい。

感染症数理モデルの歴史

1927 年に英国のケルマックとマッケンドリックは微分方程式によって、人口集団における一回の感染症流行を記述するモデル（SIR モデル）をはじめて定式化して、それが現実の流行曲線をよく再現することを示した。その後、彼らは1939 年までに5 編のシリーズペーパーを表して感染症数理モデルの基礎を築いた[5] [6]。戦間期のケルマックとマッケンドリック業績は、戦後、確率論や生物統計学の一部で継承されてはいたが、その真の姿はほとんど1970 年代にいたるまで知られていなかった。

ようやく70 年代末に欧州の研究者を中心に数学的な見直しが進み、主にオランダ、ドイツの数学者によって、1927 年論文の含意が明らかになって、閾値定理が厳密に確立された。次いで、1990 年にDiekmann, Heesterbeek, Metzによって与えられた次世代作用素を用いた基本再生産数の一般的定義は、感染症数理モデルにおけるおおきな飛躍になった[7]。実際、感染症数理モデルのその後の数学的研究は、すべてこの基礎の上にできたと言って過言ではない。当時の欧米の研究状況をみると、1973 年に設立されたアメリカ数理生物学会をはじめとして、ようやく80 年代に数理モデルによる生命現象の研究という数理生物学が勃興し、感染症も有力な研究分野として認識されてきたところであった。この動きは、欧州、日本に波及して、日本では1989 年に、現在の日本数理生物学会(JSMB) の前身である、数理生物学懇談会(JAMB)が、寺本英、山口昌哉の両京大教授によって組織された。欧州の数理生物学会（ESMTB）の発足はそれに遅れて1991 年である。

90 年代における日本の公衆衛生上の最大の課題はエイズの流行であった。エイズは古い起源があるといわれるが、パンデミックとなったのは1980 年代後半であり、日本では1989 年にエイズ予防法（旧）ができて、感染者統計が整備されるようになった。エイズ危機において注目すべきは、感染症数理モデルが流行の予測や予防政策に、はじめて広く利用されるようになったことであり、同時に、それまで必ずしも数理生物学や疫学を研究していたのではない数理科学者が多数この問題に参入したことである。このことによって、感染症数理モデル研究の裾野はひろがり、研究は大きく進歩した。

しかし日本にはそうした研究をおこなう理論・数理疫学のチームは現れず、そのことの問題性が意識化されることもなかった。日本のHIV/AIDS 流行はきわめて緩慢であり、サイズも小さかったから、理論疫学的対応の不備は表面化することはなかったのであるが、このときに理論的キャッチアップがされなかったことは、その後にも大きな影響を与えていることは注意すべきである。実際、時間スケールは全く異なるが、HIV の流行構造は、現在の新型コロナと似たところがあった。新型コロナウィルス感染も無症候性である場合が多く、しかもその潜伏期間に感染性を有している。したがって、症候性患者として観測されたものの背後に、感染源となる多数の未観測の感染者が存在している。しかも、新型コロナの流行は、エイズよりも数百倍も速いため、流行の急激な展開に対応するリアルタイムの解析が必要とされる。日本の疫学において、HIV の理論疫学が十分に理解され、ルーチンと化していたならば、今日の新型コロナ問題における感染症数理モデル分析は、よりはやく広汎におこなわれたであろうことは想像できる。

エイズ危機の後も、2001 年にはBSE（牛海綿状脳症）、2003 年SARS（重症急性呼吸器症候群）、2005 年鳥インフルエンザ、2009 年豚インフルエンザ、2012 年MERS（中東呼吸器症候群）等のように、新興・再興感染症が相次いだが、感染症流行の現場において、感染症数理モデルを活用するという「政策実装」は、少なくとも日本では、進まなかった。そのためには、感染症対策の現場を知悉しながら、数理モデル構築やリアルタイムデータ解析をおこなえる研究者の出現が必要であったが、そもそも、数理生物学における感染症数理モデル研究は、定性的な数理解析が主であり、新しい現象の発見や解釈、数学的命題の証明が目的であって、政策に必要な数字を利用可能なデータから算出するという実践的研究がほとんどなされていなかった。

その一方で、HIV 危機以降も変わることのなかった日本の公衆衛生学、疫学の教育・研究現場においては、感染症数理モデルが教えられることもなく、現場と理論をつなぐ回路もなかった。唯一の例外は、北大（現京大）の西浦博教授の研究室であった。西浦教授は2000 年代後半から、感染症数理モデルの政策実装の必要性を訴え、感染症行政への協力をおしまずに実践的研究をおこなうとともに、感染症数理モデルを教育するサマースクールを主催して、研究者、実践者の養成にのりだしていた。しかしながら、それは例外的な個人的努力にとどまり、感染症対策における数理科学利用を制度的にサポートする体制がまったくないままに、今回のCOVID-19 を迎えたのである。

COVID-19 への適用

さて、今回のCOVID-19 においては、政府専門家会議の正式メンバーではないが、それに直属する形で西浦教授とその研究室メンバーが厚労省の対策室に詰めて、リアルタイムで感染症数理モデルによるデータ分析と予測という政策実装をおこなうことになった。その結果は政府の政策にも多大の影響を与えることになったことは記憶に新しい。これは日本の感染症対策において画期的なことであったが、世界的に見ても、これほどのパンデミックにおいて、世界各国でひろく数理モデルが政策的判断に利用されるようになったことは初めてであろう。実際、各種のプレプリントサーバに日々アップされる数理分析論文は空前の量である。また同時に、玉石混淆とはいえ、非常に早くからSNS 上で、一般市民や他分野の研究者による各種の数理分析が見られるようになり、SIR モデルや基本再生産数という感染症数理モデルの基礎概念が急速にひろまり、自発的な解説やデータ分析が提供されるようになったことは、エイズ危機の頃とは全く異なる知識社会の新しいあり方を示すものであった。

一方で、緊急事態宣言や行動自粛政策の影響はあまりにも大きく、今回の数理モデルと感染症対策の遭遇には、予期しない問題が多数発生したことも事実である。分析情報が、大学のような政府と距離を置いた場所からではなく、ピアレビュウをおこなえるアカデミーではなく、政府機関の内部からしか発信されなかったことは、結果として国民には透明性の欠如、情報操作の疑いを抱かせ、SNS を中心に、政府の指針への批判が、数理モデルへの批判にも転化して激しい議論が展開されることになった。科学的言明と政治判断の混同による混乱も少なくなかったが、それが数理モデルを活用するためのリテラシイの不足によって助長されたことも明らかである。一方、社会経済的なファクターとの相互作用については、理論疫学の専門家も準備がなかった。理論的分析がただちに政策として適用できるわけではなく、政治的判断はまた世論の支持をうけなければ実効的たりえない。理論・数理分析の結果をいかに有効な政策に結びつけるかに関しては多くの問題を残したといえよう。

以下では、今年2 月以降、感染症数理モデルに関して話題となった問題をいくつか取り上げて筆者の私見を述べておきたい。ただしここでは、主に毀誉褒貶の激しかったSIR 型モデルによるマクロ流行動向予測に焦点を当てたい。実は、感染症数理モデルはSIR モデルに代表される力学系モデルが現象理解のコアであるが、それ以外に、それに本質的に依拠しながらも、データから感染症の基礎的パラメータを推定して、その定量的プロファイルを明らかにするデータサイエンス的、統計的なモデルや手法が多くを占めていて、そうした数理統計的手法に関しては筆者の専門外だが、世界標準の方法論として評価は確立しているといえる。したがって、下記にSIR モデルによるマクロ推計への批判を取り上げるが、そうした批判には首肯すべき点があるにしても、感染症数理モデルや数理疫学全般への批判にはとうていなり得ないことをあらかじめ強調しておきたい。感染症の定量的理解と感染症数理モデルは不可分であり、前者は流行制御のために不可欠である。

SIR モデルとその批判

2020 年4 月15 日に、メディアは、COVID-19 の感染拡大で、人と人との接触を減らすなどの対策を全く取らない場合、国内では重篤患者が約85 万人に上り、半数が亡くなる恐れがあるとの試算を厚生労働省のクラスター対策班の西浦博教授が公表した、と報道した。このことは大きな衝撃を持って受け止められたが、その計算の基礎は多状態のSIR モデルであった。使用されたモデルは、重症化割合や、そこからの致命率を考えるなど、単純なスカラーSIR モデルより詳細なものではあるが、その本質はかわらない。神戸大学の國谷紀良准教授も、すでに2 月段階でSEIR モデルによる計算で同様な結果を得ている[8]。要するに、SIR 型のモデルを固定パラメータで使用する限り、日本人口全体をホストとして一様な混合状態にあるものと仮定した上で、基本再生産数としてR₀ = 2.5 程度を設定すれば、巨大な感染ウェーブが発生して、感染の自然収束までに9 割方の人口が感染してしまうという結論は、ほぼ動かないのである。

しかし、一方で、致命率が無視できないような感染症において、人々が回避行動をとらないということはない。したがって接触頻度という社会的変数を含む感染伝達係数は時間的に不変であるはずはない。また入院、治療、隔離などの影響もある。さらに根本的なことに、ホスト個体群は一様に混合しているわけではなく、感染過程に関わる人口サイズそのものが可変的であるとも考えられる。固定パラメータを用いることは、人々の回避行動や政策的介入効果などを反映することは出来ない。要するに、自律的力学系モデルによる計算は、人口学でいう「投影」(projection) であって、R₀ = 2.5、世代時間が2 週間たらず、というパラメータをもつ感染個体群が潜在的に有する成長力を可視化させてみせる試算である。パラメータの時間依存性と人口の異質性によって、その計算結果がそのまま実現することはない。にもかかわらず、そうした計算がまったく荒唐無稽ということもできない。自粛行動や政策が緩むとただちに感染者の指数関数的増加が再開されることから見ても、投影モデルが示すような大きな成長ポテンシャルを感染者集団が有していることは明らかである。これは投影結果を速度計としてイメージすればわかりやすい。ある瞬間における時速100 キロという速度は、1 時間後に100 キロ先へ移動しているという予測としては、ほとんど常にはずれるが、システムの状態の指標としては非常に有効である。

したがって、多くの場合、固定パラメータを用いた力学系モデルによる推計よりは、現実の流行はずっと小規模にとどまるのが通例である。実際、日本における流行の最初の波は報告ベースでは4 月7 日の緊急事態宣言の直後にピークアウトして収束に向かった。検査数が限られていたために発症者数も全数把握されていたとは思われない。その点を考慮に入れたとしても、エピカーブとしては予想外に小さな規模におさまったことから、巨大なエピカーブを予想させたSIR モデルに対して厳しい批判が集中した。緊急事態宣言による経済的ダメージが大きかったことが、その批判に拍車をかけたことは言うまでもない。同時に、推定された発症ベースでは緊急事態宣言の前にピークがあったと考えられるため、緊急事態宣言は効果がなかったのではないか、という批判も現れた。

しかし西浦教授が主張した接触頻度の8 割削減という目標に沿って感染伝達係数パラメータを削減すれば、2 月から5 月末までの第一波の流行パターンをSEIR モデルによっておおむね再現できることが、神戸大学の國谷准教授による計算によって示されている[9]。その意味では、3 月から緊急事態宣言にいたる自粛行動のたかまりを緊急事態宣言があとおしすることによって、流行抑制が実現されたというシナリオは十分に可能性がある。すなわち、パラメータ時変SEIR モデルは、流行曲線の再現に有効である。

最近公開されたGoogle の予測は、SEIR モデルを基本モデル採用して、パラメータ変動を過去データから機械学習によって生成することによって、近未来の流行動向予測をおこなっている[10]。また米ワシントン大学の保健指標評価研究所（IHME）による推計もSEIR モデルを修正して用いている[11]。人口の様々な異質性がブラックボックスである段階では、SEIR モデルを骨格としたパラメータ時変モデルは妥当な推計方法といえよう。

非標準的予測

一方、SIR モデルによらず、データへの数学的曲線あてはめによる流行予測が、大阪大学の中野貴志教授によって提案され、その主張は「K 値」という指標によって人口に膾炙することとなり、大阪府や神奈川県においては参考指標として採用され、行政的影響を持つこととなった[12]。K 値モデルの本質は累積症例数曲線をゴンペルツ曲線とみなすことであり、日本のみならず、諸外国のデータに対しても、とくに初期からある時期までの累積感染者数に対しては、ゴンペルツ曲線がよく当てはまったという報告が、他の研究者からもなされている[13] [14]。したがって、法則性の発見という意味では、このような研究には意義がある。

しかし当然のことながら、流行過程がながびき、流行波が再帰、拡大するようになれば、一つの曲線でデータを再現することは不可能であり、いくつもの小流行の重ね合わせとして表現するほかはない。そのことは必ずしもモデルの欠陥とはいえないが、流行の要素ともいうべき各ゴンペルツ曲線を生成するメカニズムが解明されない以上、事後的にデータを再現することができても、現象の因果的理解には寄与しないし、流行予測としては機能しないであろう。

もともと曲線のあてはめは現象記述モデルであり、人口の行動変化の影響を取り入れることの出来ない先験的な非動学的モデルである。自然科学であれば、そのような現象記述法則が、頑健かつ普遍的であることが検証されれば、さらにその法則を生み出すより原理的な発展方程式の探求にむかうはずである。天体力学で言えば、現象記述法則がケプラーの法則であり、原理的な発展方程式はニュートンの運動方程式である。しかしながら、上述のように、現象記述としてもゴンペルツ法則は十分に普遍的でも頑健でもない。

したがって、こうしたモデルが、研究的に利用されることには問題はないが、そこから現実的な感染症対策に関する含意を引き出すには慎重でなければならない。感染症の流行問題を、あたかも天体力学のケプラー問題のごとく語ることで、流行がヒト集団の社会的応答から独立な、純粋な自然法則のように記述できると強調することは、介入行為の有効性を否定し、行動変容の要求水準を低下させ、流行の「早期の自然収束」を過信させる政治的結果をもたらすことになったことが問題なのである。誤解のないように言い添えれば、「自然収束」そのものは、感受性人口の補充がなければ、どのような感染症ダイナミクスにも起きることであるが、ここでの「早期の自然収束」は、SIR モデルが予想するようなテンポよりはるかにはやい収束が、介入行為なしに自発的に発生するという意味である。

そのような仮説自体は検証に値するし、以下に述べるように人口の異質性によってもたらされる可能性はある。しかし当面、第二波以降の経験が示していることは、介入行為の手を緩めればただちに流行が再興されるということであり、次第に大きくなる流行波に対して、集団免疫から十分に遠い状況では、「早期の自然収束」を期待することがまったくできない、ということであろう。数理モデルの誤った解釈が、感染症対応において行政に後手を取らせる結果になった可能性があるとすれば残念なことである。

集団免疫閾値をめぐって

理論疫学における基本的な原理は、感染症数理モデルによって裏付けられた閾値原理である。すなわち、完全な感受性集団において基本再生産数R₀が定義され、少数の感染者が発生した場合、R₀ > 1 であれば流行（感染者サイズの持続的拡大）が発生するが、R₀ < 1 であれば、流行は自然減衰して消滅する。全体が感受性である封鎖人口集団が超臨界R₀ > 1 であれば、少数の感染者の出現が大きな流行を作り出す。このとき、ホスト集団にワクチン接種をおこなって部分免疫化をおこなうとしよう。一様な個体群を想定して、割合ϵ ∈ [0, 1] が免疫化されたとすれば、実効再生産数は(1－ϵ) R₀ となるから、これが劣臨界となるためには

となればよい。この臨界免疫化割合ϵ* が集団免疫閾値に他ならない。ホスト集団の免疫化割合が、これをこえれば、流行は減衰して収束に向かうことになる（付録参照）。

このことを流行曲線に沿ってみてみると、すべてが感受性である集団で自然な流行が起きた場合、ピークに達した時点までに感染して獲得免疫を得た人口割合が集団免疫閾値になる。このとき残っている感受性人口割合は1 / R₀であり、感受性人口割合がそれを下回っていれば、流行の再拡大はおきない。それゆえ、流行がロックダウンなどによって人為的に緩和され、収束しても、残った感受性人口割合が1 / R₀ を超えていれば、集団免疫化は不十分であり、感染者の発生によって流行の再拡大がおきる。

また自然な流行軌道においては、ピーク時点で流行の拡大はとまるが、流行は減衰しながら持続するので、流行が終わるまでの最終的な罹患割合（最終規模）は集団免疫閾値よりはるかに大きい。たとえば、R₀ = 2.5 であれば、臨界免疫化割合は60 パーセントであるが、最終規模は90 パーセントである。そこで、仮にこのモデルを1 億2600 万の日本人人口が感受性であるとして、適用できるとすれば、R₀ = 2.5 のもとで、最終的な罹患規模は1億人を超え、その致命割合(infection fatality rate) を0.5 パーセントとすれば、50 万以上の死者が出ると概算されることになる。

以上が古典的な集団免疫論であるが、COVID-19 においては、2020 年春の段階で、獲得免疫による集団免疫化に関しては、観測された基本再生産数から(6.1) によって計算される古典的な集団免疫閾値よりもずっと低いところに閾値があるのではないかという議論がいくつかあらわれていた。Britton 等[15] は多状態SEIR モデルを使い、 Gomes 等[16] は連続的なリスク変数をもつSEIR モデルを使用するという違いはあるが、いずれも内的異質性を持つホスト集団における流行においては、高い感受性をもつ集団から選択的に流行が発生することで、より低い感受性集団が残されていき、一様な集団よりも低い累積感染者割合で閾値が達成されることを示唆している。このような想定は合理的であるが、想定計算は可能であっても定量的な評価が可能な状態にはなく、集団免疫論の基礎は意外に曖昧である。ワクチン政策の最適政策を考えていく上でも、行動学的、免疫学的な人口の異質性への理解を深めることは今後ますます重要となろう。

集団免疫論は封鎖人口集団を前提としているから、外部との人口の出入りのある部分人口集団に対しては、従来の集団免疫閾値をそのまま適用して考えることは出来ない。劣臨界の人口集団においても、外部から感染者の流入があれば、流行は持続する。また、既にいくつか報告されているように、SARS-CoV-2 の感染から回復しても再感染があるようである。再感染がある場合、再感染の感受性の程度によっては、流行がエンデミックとなることが数理モデルによって予想される[17]。さらに、再感染者が無症候性であるとすれば、根絶は非常に難しいと思われる。

大量検査と隔離の問題

日本の感染症対策におけるひとつの重要な論点は、PCR 検査を一般人口に対して大量に実施して流行制御をおこなうかどうか、ということであった。中国、台湾、ニュージーランドなどでは、流行の初期から大量検査(massive testing) を導入して、流行の抑え込みに成功している。日本では、接触者調査によるクラスター対策が当初から重視されて、事前の感染率の低い人口に対する普遍的な大量検査は多くの偽陽性をうみだし、医療現場に混乱をもたらすだけであるとして、否定的な議論が多かった。

流行初期では検査における陽性的中率が非常に低いことは事実であるが、実際には、中国やオーストラリアにおける大量PCR 検査の結果から推定される検査特異度は、0.9999 以上という非常に高い値を示しており、検体汚染などのヒューマン・エラー等がない限り、PCR 検査の特異度は、おおむね100 ％（偽陽性はおおむねゼロ）であるという指摘が、経済学者を中心になされてきている[18]。そのような場合には的中率はほぼ100 パーセントであり、偽陽性者隔離の問題はおきない。

また大量検査の流行抑止手段としての有効性に関しては、國谷・稲葉[4],[19] が、定常的な検査による隔離政策の効果を数理モデルで検討した。実効再生産数R_e に対する検査率と社会的距離拡大政策の効果をみてみると、【図表1】に示すように、検査率k がおよそ0.23 以上であればR_e < 1 であり、流行の制御が可能と考えられる。特に、検査率k に対してR_e が下に凸で減少していることに注意すると、検査率がもともと低い集団で検査率を高めることに大きな効果があるという示唆が得られる。さらに、社会距離拡大政策を同時に行うことで、流行制御に必要となる臨界的な検査率の値を実用的な水準まで低くすることができることに注目すべきである。

図表1

異なる社会距離拡大政策（r = 0, 0.3, 0.5）のもとでの検査隔離の検査率k に対する実効再生産数Re

以上のことから、流行規模にかかわらず、普遍的大量検査をおこなうことは、非常に有効な制御手段であると考えられる。また十分な検査率を維持することによって、陽性率から流行動向をモニターすることができるという意義があることはいうまでもない。感染の広がりとともに接触者調査にもとづくクラスター対策では抑制は困難になっているにもかかわらず、大量検査の流行抑止効果に対する懐疑的な態度が、その後の各国における経験によって修正されず、検査態勢の充実を遅らせる政治的効果を生み出したとしたら残念である。

おわりに

今回の緊急事態宣言やロックダウンのような非薬剤的制御手段は莫大な経済的コストが必要であり、疫学的観点から適切な政策が、かならずしも実行可能ではないし、他の基準に照らして最適とも限らない。感染症数理モデルの社会経済変数との接合はまったく用意されていなかったことは指摘しておかねばならない。国家的規模の感染症流行のような非常事態において、可能な社会的目標に対して、どのように政策を組み合わせていくべきかは、社会経済的な戦略研究（OR) の問題であり、従来の感染症数理モデルの問題意識を大きく超える課題であったといえる。

今回の新型コロナ問題を通じて、感染症数理モデルは、社会現象を制御する手段として認知されるという歴史的な地点に達した。それと同時に、その利用に対する厳しい批判もおきた。実際、純粋な理論的立場からしても、現実の人口のあり方は複雑多様であり、リアルな感染症ダイナミクスには未知の部分が非常に大きいことはいうまでもない。現実を単純化した理論による最適制御が、必ずしも良い結果をもたらさないことも強調しておく必要がある[1]。

しかしながら、これまで述べたように、感染症数理モデルは、流行を理解し、合理的な対策を立案するために不可欠な思考の枠組みを提供していることは間違いない。したがって、現状におけるその限界をわきまえつつ利用していく科学的体制とリテラシイを涵養していくことが重要であろう。とりわけ感染症疫学の教育と行政の現場においては、数理モデル分析は標準的なルーチンとして定着させる必要があるだろう。

［引用文献］

1. 稲葉寿 (2020), 感染症数理モデル私史, 「科学」vol. 90, no. 10: 0909-0914.
2. O. Diekmann, J. A. P. Heesterbeek and T. Britton (2013), Mathemat-ical Tools for Understanding Infectious Disease Dynamics, Princeton University Press, Princeton and Oxford.
3. H. Inaba (2017) Age-Structured Population Dynamics in Demography and Epidemiology, Springer.
4. 稲葉寿（編著） (2020), 「感染症の数理モデル」増補改訂版, 培風館.
5. W. O. Kermack and A. G. McKendrick (1927), Contributions to the mathematical theory of epidemics I, Proceedings of the Royal Society 115A, 700-721: reprinted in Bulletin of Mathematical Biology 53(1/2), 33-55 (1991).
6. W. O. Kermack and A. G. McKendrick (1932), Contributions to the mathematical theory of epidemics II. The problem of endemicity, Pro-ceedings of the Royal Society 138A, 55-83: reprinted in Bulletin of Mathematical Biology 53(1/2), 57-87 (1991)
7. O. Diekmann, J. A. P. Heesterbeak and J. A. J. Metz (1990), On the De nition and the computation of the basic reproduction ratio R₀ in models for infectious diseases in heterogeneous populations, J. Math. Biol. 28: 365-382.
8. T. Kuniya (2020), Prediction of the epidemic peak of coronavirus dis-ease in Japan, 2020, Journal of Clinical Medicine 9: 789.
9. T. Kuniya (2020), Evaluation of the effect of the state of emergency for the first wave of COVID-19 in Japan, Infectious Disease Modelling 5: 580-587.
10. Google COVID-19 感染予測　https://datastudio.google.com/u/0/reporting/8224d512-a76e-4d38-91c1-935ba119eb8f/page/ncZpB
11. IHME COVID-19 Forecasting Team, Modeling COVID-19 scenarios for the United States, Nature Medicine, Published: 23 October 2020.
12. T. Nakano and Y. Ikeda (2020), Novel Indicator to ascertain the status and trend of COVID-19 spread: Modeling study, J Med Internet Res vol. 22, iss. 11, e20144.
13. M. Catara, S. Alonso, E. Alvarez-Lacalle, D. Lopez, P. J. Cardona1 and C. Prats (2020), Empiric model for short-time prediction of COVID-19 spreading, medRxiv preprint doi: https://doi.org/10.1101/2020.05.13.20101329.
14. A. Ohnishi, Y. Namekawa and T. Fukui (2020), Universality in COVID-19 spread in view of the Gompertz function, medRxiv preprint doi: https://doi.org/10.1101/2020.06.18.20135210.
15. T. Britton, F. Ball and P. Trapman (2020), A mathematical model reveals the in uence of population heterogeneity on herd immunity to SARS-CoV-2, Science published on line June 23, 10.1126/sci-ence.abc6810.
16. M. G. Gomes, et al. (2020), Individual variation in susceptibility or exposure to SARS-CoV-1 lowers the herd immunity threshold, preprint.
17. 稲葉寿 (2020a), 集団免疫論を超えて、「数学セミナー」vol. 59, no. 9: 19-25.
18. 小黒一正 (2020), PCR 検査体制の拡充と偽陽性の問題、URL: https://www.rieti.go.jp/jp/columns/a01_0611.html
19. T. Kuniya and H. Inaba (2020), Possible effects of mixed prevention strategy for COVID-19 epidemic: massive testing, quarantine and so-cial distancing, AIMS Public Health 7: 490-503.

付録：SIR モデルの基礎

Kermack-McKendrick のSIR モデルを最も単純化した形態である常微分方程式システムを紹介しておこう。本来のモデルは偏微分方程式の境界値問題として定式化されるべきものである[3] [4]。

いまサイズN の封鎖人口を想定して、S(t) を時刻t における感受性人口サイズ、I(t) を感染人口サイズ、R(t) を感染から回復した人口サイズとすれば、Kermack-McKendrick のSIR モデルは以下のように定式化される：

ここで、β は感染伝達係数、γ は回復率であり、タイムスケールが違うために、人口学的な要素（出生、死亡、移動）は無視している。β のかわりにNを外に出してβ/N を用いる場合もあるが、N = S +I +R は定数なので定性的な差はない。βN はサイズN の感受性個体群におかれた感染1 個体の単位時間における平均接触数と一回の接触あたりの感染成功確率の積であり、単位時間に生産する二次感染者数を与える。このとき感染者や回復者のいない定常状態は(S, I, R) = (N, 0, 0) であるが、そこでの線形化方程式は、

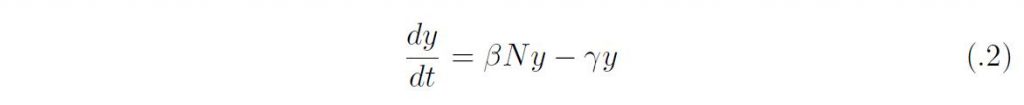
となる。y は初期の感染人口サイズであり、基本再生産数は

としてえられる。実際、R₀ は一人の感染者がその全感染性期間のあいだに生産する二次感染者の平均数に他ならない。初期感染者の増加率はr = βN ーγであるから、r = γ(R₀ ー 1) となる。成長率の正負は、R₀ ー 1 の正負に対応している。すなわち、R₀ > 1 であれば、感染症のない平衡状態(N, 0, 0) は不安定になり、流行の拡大が始まるが、R₀ < 1 であれば安定であり、感染者数は自然減衰する。これが侵入の閾値原理に他ならない。

ワクチンによる感受性人口の免疫化の割合をϵ ∈ [0, 1] としよう。このとき、部分免疫化されたホスト集団の平衡状態は((1 ー ϵ)N, 0, ϵN) となる。この定常状態における線形化方程式は、

となるから、その実効再生産数（なんらかの介入行為がある場合や、流行途中の二次感染者再生産数）は、

となる。したがって、R_e < 1 となるようにϵ を選べば、感染症の侵入は防ぐことができることになるから、

となればよい。このとき、ϵ* を臨界免疫化割合（集団免疫閾値）とよぶ。すなわちϵ より大きな割合の感受性ホスト人口が免疫化されれば、流行はおきない。

集団免疫閾値を流行における獲得免疫という側面からみてみよう。(.1) において、dI/dt をdS/dt でわれば、(S, I) 相平面上の軌道方程式として、

が得られる。これは簡単に積分できて、C を積分定数とすれば、

という軌道方程式を得る。いま初期感染者がゼロとなる極限軌道として、(S, I) = (N, 0) を通る軌道を考えると、C = N ー (γ/β) log N であり、

を得る。これは、罹患割合I/N を感受性人口割合S/N の関数として見た式に他ならない。この極限軌道はR₀ > 1 のときI = 0 となるN 以外の根S_∞ > 0をもつ。このときS_∞ = lim_t→∞ S(t) であって、S_∞=N が感染の最終規模である。このとき、

となる。最終的に罹患した人の割合として、最終規模p (final size/attack rate) を

とすれば、(.10) から、最終規模方程式

を得る。この方程式から、R₀ を与えたときの最終規模の下限が決定される。

またR₀ > 1 であれば、解軌道I = I(S) は時間とともに増加して、S* =γ/βにおいて最大値をとり、その後減少に転ずる。このピークにおいて感受性人口の割合は

になる。すなわち、全人口が感受性の状態から、感受性人口割合が1/ R₀ 以下になるということは、流行による獲得免疫割合が1 ー 1/ R₀ = ϵ* 以上となることであり、流行は自然減衰にむかうことを意味している。このピーク時点以降、残った感受性人口における感染者の再拡大はない。換言すれば、非薬剤的制御によって人為的に流行を収束させても、残された感受性人口割合が1/ R₀ を超えているならば、感染者の侵入によって流行の再燃がおきる。

最後にSEIR モデルを紹介しておこう【図表2】。感染直後の状態は感染性のない潜伏期間(latent class) であるとして、その人口サイズをE とすれば、

というモデルが得られる。ここで、ϵ は感染性状態への推移強度であり、1/ ϵが感染性を得るまでの待ち時間（E クラスでの平均滞在時間）を与える。

図表2

Transfer diagram for SEIR model

もしもE を感染したが発症前である状態(presymptomatic) と考え、I を症候性(symptomatic) と想定すれば、SARS-CoV-2 の場合、E とI の双方に感染性があるから、SEIR モデル(.14) におけるβSI の項は(β₁E +β₂I)S のように置き換えられる。ここでβ₁ は発症前の伝達係数であり、β₂ は発症者の伝達係数である。このような発症ベースのモデルは[4] で検討されている。

関連記事