Self-supervised learning of materials concepts from crystal structures via deep neural networks

Yuta Suzuki; Tatsunori Taniai; Kotaro Saito; Yoshitaka Ushiku; Kanta Ono

doi:10.1088/2632-2153/aca23d

1.Â Introduction

The diverse properties of the inorganic materials originate from their crystal structures, i.e. the atomic-scale periodic arrangements of elements. How structures determine low-level material properties such as the band gap and formation energy is well studied as the structure-property relationship [1, 2]. On the other hand, the materials science literature often discusses 'superconductors' [3], 'permanent magnets' [4], or 'battery materials' [5], referring to their higher-level properties, or functionality. Nevertheless, understanding what structures exhibit such functionality, or understanding the structure-functionality relationship, is a fundamental question in materials science. We call this functionality-level material similarity 'materials concepts'. Traditionally, materials science has sought new materials by experimentally and theoretically understanding specific functionalities of materials in a bottom-up fashion [1â5]. However, this labour-intensive narrowly focused analysis has prevented us from grasping the whole picture of the materials space across various materials concepts. For next-generation material discovery based on the structure-functionality relationship, we argue here the need for a top-down unified view of crystal structures through materials concepts. We pursue this ambition by learning a latent representation space of crystal structures. Thus, this representation space should ideally both (a) recognise materials concepts at scale and (b) be equipped with a functionality-level similarity metric between materials. We here utilise multi-modal structural attributes of materials to effectively capture structural patterns correlated to material functionality (figure 1). The underlying hypothesis here is that materials concepts are the intrinsic nature of crystal structures, and therefore, deeply analysing the structural similarity between materials will lead to capturing functionality-level similarity.

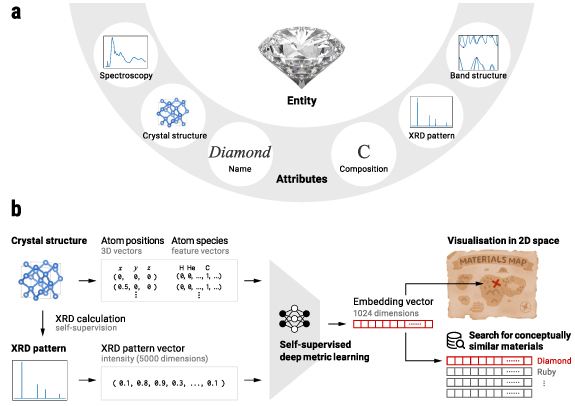
Figure 1. Refer to the following caption and surrounding text. — **Figure 1.**Â Our strategy for learning materials concepts. (a) Diamond as an example material and its various structural attributes showing different information of diamond in different data forms, or modalities. Since each attribute has its own advantages and disadvantages in expressing a material, using multiple attributes for a material can provide a more comprehensive view of the material. Particularly, the combination of the crystal structure and the x-ray diffraction (XRD) pattern, which we employ in this study, is known to well reflect two complementary structural features of materials, the local structure and the periodicity [1]. (b) Our goal is to represent each material as an abstract constant size vector (embedding) whose distances to other embeddings reflect conceptual (functionality-level) similarities between materials. These embeddings allow us to visualise the materials space intuitively and also to search for conceptually similar materials given a query material. We learn embeddings from pairs of crystal structures and XRD patterns in the framework of deep metric learning. This cross-modal learning approach trains deep neural networks by teaching them that each pair should represent the same material entity. Because the XRD pattern can be theoretically calculated from the crystal structure, this learning can be performed in a self-supervised manner without any explicit human annotations for the materials dataset.
Download figure:
Standard image High-resolution image

Figure 3(a) highlights key results by our representation space, which maps the crystal structures of materials to abstract 1024-dimensional vectors. For visualisation, these vectors were reduced to 2D plots in the figure using a dimensionality reduction technique called t-distributed stochastic neighbour embedding (t-SNE) [6]. We target 122â543 inorganic materials registered in the Materials Project (MP) database (amounting to 93%) to capture nearly the entire space of practically known inorganic materials. These crystal structures themselves contain information about their functionalities implicitly. However, they do not explicitly tell us what structural patterns lead to specific material functionalities such as superconductivity due to complicated structure-functionality relationships. Nevertheless, these materials form clusters of various materials concepts in the space (see annotations in figure 3(a)), showing the success of our representation space capturing structural patterns correlated to material functionality.

When analysing diverse relationships entangled with complex features in large-scale data, machine learning (ML) and deep neural networks (DNNs) are key technologies [7, 8]. Indeed, these technologies often surpass human ability in recent materials informatics work. For example, when extracting features from materials data for complex tasks such as physical property prediction, learning-based descriptors [9â18] have been shown to outperform traditional hand-crafted descriptors [19â24].

Likewise, representation learning is gaining attention for understanding human-incomprehensible large-scale materials data [25â29], visualising the materials space [25, 27â30], and generating crystal structures [31â36]. These material representations aim to map the abstract, comprehensive information of each material into a vector called an 'embedding'. Our work has the same purpose as that of embedding learning. However, to date, neither descriptor nor embedding learning explicitly learns the underlying relationships or similarities between materials. Particularly, existing embeddings [25â29] are learned indirectly as latent feature vectors in an internal layer of a DNN by addressing a surrogate training task (e.g. the prediction of physical properties [27, 28], a task of natural language processing (NLP)[26] or its variants [25, 29]). In such an approach, it is unclear from which layer we should obtain the latent vectors or which metric we should use to measure the distance/similarity between them.

Capturing abstract concepts of materials via learning structural similarities between them is analogous to word embedding learning [26] in NLP. Similar to materials concepts, meanings of words in natural languages often reside in complex and abstract notions, which prevent us from acquiring precise definitions for them. Word embeddings then attempt to capture individual word concepts, without being explicitly taught, by absorbing our word notions implicitly conveyed in the contexts provided by a large-scale text corpus. Once optimised, similarities/distances between embeddings express their concepts, e.g. the embedding of 'apple' will be closer to those of other fruits such as 'grape' and 'banana' than 'dog' or 'cat'. Our crystal structure embedding shares a similar spirit with word embedding in that both attempt to capture abstract concepts via learned similarities. More importantly, we exploit a large-scale material database as a corpus of materials that implicitly conveys important structural patterns in its contexts of crystal structures, as analogously to word embedding. These structure instances of diverse kinds of materials, even without explicit annotations about their properties, should contain tacit but meaningful information about physics and material functionality that can guide the learning of ML models. From an ML perspective, such a learning strategy is called self-supervised learning [37], in which the data of interest themselves provide supervision.

In this study, we demonstrate the large-scale self-supervised learning of material embeddings using DNNs. In essence, we follow the principle that the structure determines properties and aim to discover materials concepts purely from crystal structures without explicit human supervision in learning. To this end, we use a collection of crystal structures as the only source of training data and do not provide any annotation regarding specific material properties (e.g. class labels such as 'superconductors' and 'magnets', or property values such as superconducting transition temperature and magnetisation). Furthermore, unlike existing methods for material embedding learning, we explicitly optimise the relationships between embeddings by pioneering the use of deep metric learning [38]. Metric learning is an ML framework for learning a measure of similarity between data points. Unlike the common practice of metric learning performed in a supervised fashion using annotated training data [38], we allow our ML model to be learned from the unannotated structural data in a self-supervised fashion.

2.Â Results

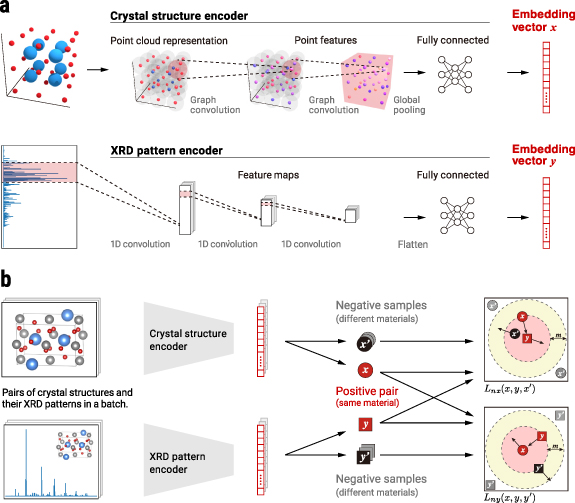
Our key idea for self-supervised learning, illustrated in figure 2(a), is to learn unified embedding representations for paired inputs expressing two complementary structural features characterising materials: the local structure and the periodicity [1]. In our model, the local structure is represented by a graph whose nodes and edges stand for the atoms and their connections. The periodicity is represented by a simulated x-ray diffraction (XRD) pattern, which can be theoretically calculated from the crystal structure using Bragg's law and Fourier transformation [1]. We simultaneously train two DNN encoders by enforcing them to produce consistent embeddings across the two different input forms. This training strategy follows a simple optimisation principle: (a) for a positive pair in which the input crystal structure and XRD pattern come from the same material, the Euclidean distance between two embedding vectors is decreased, and (b) for a negative pair in which these inputs come from different materials, the distance is increased. We implement this principle in the form of a bidirectional triplet loss function, as illustrated in figure 2(b). For the detailed method protocol, see section 5.

Figure 2. Refer to the following caption and surrounding text. — **Figure 2.**Â Our self-supervised deep metric learning for materials. (a) The proposed network architecture, including two separate DNNs to encode the crystal structures and XRD patterns into unified embedding vector representations. To account for respective input data forms (figure 1(b)), the crystal-structure encoder employs a DNN for graphs while the XRD pattern encoder employs a 1D convolutional neural network. (b) A schematic view of our bidirectional triplet loss. This triplet loss is used to simultaneously train the two DNN encoders to output embeddings that are close together when the input crystal structures and XRD patterns are paired (red-coloured x and y ) and far from one another when the inputs are not paired ( x and y vs others). More details are given in section 5.
Download figure:
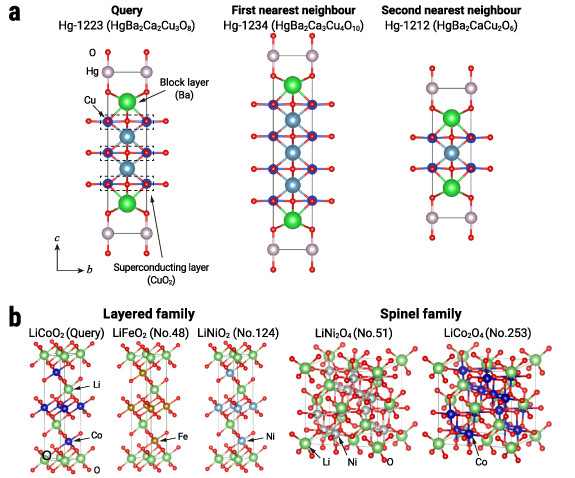
Standard image High-resolution image

Figure 3. Refer to the following caption and surrounding text. — **Figure 3.**Â A map of the materials space. (a) A global map of the materials space, plotted via a t-SNE visualisation of the embeddings. Each point corresponds to an individual material that is encoded by the trained crystal-structure encoder. The map was annotated with cluster labels through manual inspection. Our materials map is publicly accessible via an interactive website (https://github.com/quantumbeam/materials-concept-learning). (b) A close-up view of a cluster of cuprate superconductors in the materials space. (c) Crystal structures of Y-123 and Y-124 families, which are closely distributed in (b). The CuO chain in Y-123 and the double CuO chain in Y-124, which is similar to vertically repeating Y-123, are important features of YBCO superconductors.
Download figure:
Standard image High-resolution image

By design, we minimise human knowledge of specific materials concepts in both the data source and training process, with the belief that materials concepts are buried in crystal structures. This design principle enhances the significance of the resulting embedding highlighted earlier (figure 3(a)). It captures profound materials relationships through simple data and optimisation operations considering only general and elementary knowledge of materials such as crystallographic data and Bragg's law. The results suggest that materials concepts can be exposed in deeply-transformed abstract expressions unifying the complementary factors, i.e. the local structure and periodicity, of crystal structures.

The following analyses examine the embedding characteristics more carefully to see if the embedding space has the two desired features mentioned above. Specifically, we qualitatively analyse (a) the global embedding distribution using t-SNE visualisation and (b) the local neighbourhoods around some important materials using the learned similarity metric between crystal structures. In the latter, a superconductor (Hg-1223), a lithium-ion battery material (LiCoO₂), and some magnetic materials serve as our benchmark materials because of the high social impacts and the diverse properties yet complex structures of these material classes. These analyses also demonstrate the usefulness of our materials map visualisation and similarity metric for material discovery and development.

2.1.Â Global distribution analysis

Careful inspection of the embedding space (figure 3(a)) reveals various clusters consistent with our knowledge of materials. Here, we note several interesting examples. A series of clusters corresponding to double perovskites (A₂BB^Ê¹X₆) with different anions, X, exists along the left edge and at the centre of the map, forming a family of materials with the same prototypical crystal structure. This layout suggests that our model captures the structural similarity while properly distinguishing the local atomic environment at each site. At the lower left of the map, well-known 2D materials (transition metal dichalcogenides) form clusters in accordance with their atomic stacking structures [39]. At the top edge lies a cluster of imaginary unstable materials with extremely low-density structures (see also figure 5(a) for more details), representing one of the simplest cases of crystal structures governing physical properties. This cluster of unstable materials is an example showing that our embeddings capture materials characteristics solely from crystal structures without any explicit annotation given for training.

One exciting finding from this map is a cluster of cuprate superconductors at the left edge. This cluster includes the first-discovered copper oxide superconductor, the LaâBaâCuâO system, and the well-known high-transition-temperature ( $T_\mathrm{c}$ ) superconductors YBCO (YBa₂Cu₃O₇ or Y-123), which are located close to LaâBaâCuâO. These celebrated superconductors share a common structural feature, a CuO₂ plane, that is vital to their superconductivity [3]. The formation of this cluster suggests that our embeddings recognise this hallmark structural feature. A closer look at this cluster (figure 3(b)) further reveals the presence of subclusters with structural features linking them. Y-123 and its variant Y-124 have a non-trivial structural similarity related to the CuO chain (see figure 3(c)). In addition, we confirmed other major cuprate superconductors containing Bi, Tl, Pb, or Hg form respective clusters in accordance with their local structures called 'block layers', a key structural concept for understanding the underlying physics of cuprate superconductors [40]. The proximity of these materials on the map further supports the claim that the embeddings capture the structural characteristics and, consequently, the structure-functionality relationships between cuprate superconductors.

These findings naturally lead us to the idea that the map might be able to identify potential superconductors or other beneficial compounds that have not yet been recognised. We leave this idea as an open question and have set up a project website where anyone can dig into the embedding map to search for, or rediscover, potential compounds with preferable functionality.

The t-SNE visualisation also provides a macroscopic perspective on the materials space based on the crystal structure. The simplest indicator of success for this model is the distribution of the elements within the materials map. Because atoms and ions with similar electron configurations compose materials with the same or similar crystal structures, we expect the element distributions to show cluster-like features if our embeddings have been trained successfully. In figure 4, we highlight each element in the map and display all elements in the form of a periodic table. As expected, figure 4 clearly shows similar distributions of blue-coloured clusters in the vertical and horizontal directions. These distributions can be analogously called the 'alkali metal plateau', the '3d transition metal district', or 'rare-earth mountains' if we follow the map metaphor, indicating that the embeddings succeed in capturing the similarities of roles between elements in crystal structures. Additionally, we noticed that well-known connections between physical properties and elements can also be probed using this plotting technique (see figures 5(b) and (c) for details). Although these visualisations (figures 4 and 5) are intended to confirm expected outcomes rather than showing interesting findings, they demonstrate their potential utility, e.g. for giving researchers new insights or helping them find materials with desired properties.

Figure 4. Refer to the following caption and surrounding text. — **Figure 4.**Â Elemental distributions within the material embedding space. t-SNE plots of the embeddings are laid out on the periodic table, coloured blue or grey according to whether each material contains the corresponding element or not. Similar distributions in the vertical and horizontal directions (groups and periods) of the table indicate that the embeddings successfully capture the similarities of roles between elements in crystal structures. 'n.a.' means no material containing the element is found in our dataset.
Download figure:
Standard image High-resolution image

Figure 5. Refer to the following caption and surrounding text. — **Figure 5.**Â Physical property distributions within the material embedding space. t-SNE plots of the embeddings are coloured according to the physical properties: energy above the hull, band gap, and magnetisation. These plots show clusters of materials with similar physical properties, indicating that the embeddings capture the property similarities between materials. (a) The distribution of energy above the hull (eV). A large value of energy above the hull indicates that a material is unstable. A cluster of unstable compounds containing sparse unsynthesisable crystal structures was identified on the upper left. (b) The distribution of the band gap (eV). The distribution overlap of large-bandgap materials in this figure and oxides in figure 4 demonstrates a well-known connection between the band gap and oxygen. (c) The distribution of magnetisation (T). Materials with large magnetic moments have higher composition ratios of magnetic elements such as Mn, Fe, Co, and Ni and are particularly studied in the rare-earth permanent magnet research. The distinct yellow cluster in the top right of this figure contains intermetallic compounds of the magnetic elements and rare-earth elements (e.g. Ce, Pr, Nd, and Sm), as evident from figure 2 where the distributions of these elements overlap in this area.
Download figure:
Standard image High-resolution image

2.2.Â Local neighbourhood analysis

We next examine the local neighbourhoods of several benchmark areas to verify whether the learned metric recognises functionality-level material similarity. Since the embeddings were optimised with the Euclidean distance, we also used this metric to determine the neighbourhoods.

As the first example, we analysed the neighbourhoods of Hg-1223, a superconductor with the highest known $T_\mathrm{c}$ (134âK) at ambient pressure [42]. To our surprise, the first and second nearest neighbourhoods correspond to its close kin Hg-1234 and Hg-1212, which also have high $T_\mathrm{c}$ values (125âK and 90âK) but different block layers [40] from those of Hg-1223 (see figure 6(a)). Further investigation identified major Tl-based high- $T_\mathrm{c}$ superconductors, such as Tl-2234 ( $T_\mathrm{c}$ = 112âK), Tl-2212 ( $T_\mathrm{c}$ = 108âK), and Tl-1234 ( $T_\mathrm{c}$ = 123âK)[43], and many other superconductors occupying the top-50 neighbourhoods (see table 1). The connection between the crystal structures and $T_\mathrm{c}$ values involves non-trivial mechanisms that are not immediately evident from the crystal structures [3, 40]. The results suggest that our model effectively bridges this gap with the help of learned structure-functionality relationships that are deeply buried in the 1024-dimensional space.

Figure 6. Refer to the following caption and surrounding text. — **Figure 6.**Â Crystal structures of queries and nearest neighbours. (a) Crystal structures of the Hg-1223 superconductor and its first and second nearest neighbours, Hg-1234 and Hg-1212, in the embedding space. These are all Hg-based copper oxide superconductors with high $T_\mathrm{c}$ and are built on two important components, namely, block layers and superconducting layers. Placing these close-kin materials, yet with different numbers of superconducting layers, as close neighbours suggests that the embedding captures the conceptual similarity in their structures. See also table 1 for the top-50 neighbour list of Hg-1223, in which more superconductors with high $T_\mathrm{c}$ are found. (b) Crystal structures of the well-known lithium-ion battery cathode material LiCoO₂ and its neighbours in the embedding space. The layered and spinel families, which are two major types of the cathode materials, were identified in the neighbourhoods. See also table 2 for the list of the top-50 neighbours, in which more layered-family materials are found.
Download figure:
Standard image High-resolution image

Table 1.Â The top-50 neighbours of Hg-1223 in comparison with hand-crafted descriptors.

Â	Our embedding		Ewald sum matrix		Sine Coulomb matrix
No.	Formula	ID	Formula	ID	Formula	ID
Query	Ba₂Ca₂Cu₃HgO₈	mp-22601	Ba₂Ca₂Cu₃HgO₈	mp-22601	Ba₂Ca₂Cu₃HgO₈	mp-22601
1	Ba₂Ca₃Cu₄HgO₁₀	mp-1228579	Sr₄TlFe₂O₉	mp-1218464	Tl(CuTe)₂	mp-569204
2	Ba₂CaCu₂HgO₆	mp-6879	Ba₂La₂Ti₂Cu₂O₁₁	mp-1214655	CaLa₂BiO₆	mvc-15176
3	Ba₆Ca₆Cu₉Hg₃O₂₅	mp-1228760	CeY₄Mg₅	mp-1226574	PtC₄S₂(IO)₂	mp-1102535
4	Sr₂CaCu₂(BiO₄)₂	mp-1218930	Ba₆Nb₂Ir(ClO₆)₂	mp-558113	Ba₂FeReO₆	mp-31756
5	Ba₁₀Ca₅Cu₁₀Hg₅O₃₁	mp-1229139	Ba₆Ru₂Pt(ClO₆)₂	mp-554949	Hg(SbO₃)₂	mp-754065
6	SrCa₂Cu₂(BiO₄)₂	mp-1208800	Ba₂Nd₂Ti₂Cu₂O₁₁	mp-557043	Ba₂CuWO₆	mp-505618
7	Ba₈Ca₄Cu₈Hg₄O₂₅	mp-1228371	Ba₄ScTi₄BiO₁₅	mp-1228157	CaLa₂WO₆	mvc-15479
8	Ba₂Ca₃Tl₂(CuO₃)₄	mp-556574	La₃ZnNi₃	mp-18573	Ba₂YTaO₆	mp-12385
9	Ba₂Mg₃Tl₂(WO₃)₄	mvc-129	Zr₄WC₅	mp-1215364	TlCdTe₂	mp-998919
10	Ba₂TlV₂O₇	mvc-2978	Nd₃GaCo₃	mp-1103877	TlCuPd₂	mp-1096374
11	Sr₂YCu₂(BiO₄)₂	mp-1208863	Y₄Ti₆Bi₂O₂₁	mp-1216208	LaTlAg₂	mp-867817
12	Sr₂LaCu₂HgO₆	mp-1208803	Sm₃HoS₄	mp-1219190	In₃Au	mp-973498
13	Ba₂CaTl₂(CuO₄)₂	mp-573069	Ba₃Bi(BO₂)₉	mp-1200141	CeTlAg₂	mp-867298
14	Ba₄CaCu₆(HgO₈)₂	mvc-15237	AgRhO₂	mp-997106	Cs₂WBr₆	mp-541753
15	Ba₄Ca₄Cu₆Hg₂O₁₇	mp-1228265	YbSm₃S₄	mp-1215523	TlIn₃	mp-1187742
16	Ba₂AlTlCo₂O₇	mvc-2977	Ca₄Cd₃Au	mp-1227562	In₃Pt	mp-1184857
17	Sr₈Pr₄Cu₉(HgO₈)₃	mp-1218674	InAg₄	mp-1223819	Ca₄Cd₃Au	mp-1227562
18	Ba₆Ca₃Cu₆Hg₃O₁₉	mp-1228161	Sr₄ZrTi₃O₁₂	mp-1218457	Cd₃Pt	mp-1183641
19	Ba₈Ca₈Tl₇(Cu₄O₁₃)₃	mp-1204270	Ce₃Ni₂Ge₇	mp-1213875	Ag₃Au	mp-1183214
20	Ba₄Ca₄Tl₃Cu₆O₁₉	mp-542197	Ba₂YTlV₂O₇	mvc-2994	Mn₄BiSb₃	mp-1221739
21	Ba₆Ca₆Tl₅Cu₉O₂₉	mp-680433	Te₃Au	mp-1217358	NdTlAg₂	mp-974782
22	Ba₂AlTlCo₂O₇	mp-1266279	Nd₃Cu₄(P₂O)₂	mp-1209832	HgI₃	mp-973601
23	Ba₂Ca₂Tl₂Ni₃O₁₀	mvc-3067	Ba₄Zn₄B₁₄Pb₂O₃₁	mp-1194514	TlCdIn₂	mp-1093975
24	Ba₂Ca₂Tl₂Cu₃O₁₀	mp-653154	Ba₆Na₂Nb₂P₂O₁₇	mp-556637	CePd₂Pt	mp-1226474
25	Ba₂Ca₂Tl₂Co₃O₁₀	mvc-3021	Ba₂Tb₂Ti₂Cu₂O₁₁	mp-505223	PmHgRh₂	mp-862913
26	Sr₂CaCu₂(BiO₄)₂	mp-555855	Sc₂TlCu₃S₅	mp-1209018	Sr₂LaCu₂HgO₆	mp-1208803
27	Ba₄Tl₂Cu₂HgO₁₀	mp-561182	Eu(GaGe₂)₂	mp-1225812	NdPd₂Pb	mp-1186317
28	Ba₆Ca₁₂Cu₁₅Hg₃O₃₇	mp-1229082	AgTe₃	mp-1229041	PmTlRh₂	mp-862967
29	BaCuReO₅	mvc-7248	Sm₃GaCo₃	mp-1105102	Cd₃Ir	mp-1183645
30	Ba₂Ca₃Tl₂(FeO₃)₄	mvc-145	Nb₄Rh	mp-1220441	HgPd₃	mp-1184658
31	Sr₁₀Cu₅Bi₁₀O₂₉	mp-667638	La₃(Al₂Si₃)₂	mp-1211155	SnPd₂Au	mp-1095757
32	Ba₂Ca₃TlCu₄O₁₁	mp-1228589	Ce₂In₈Pt	mp-1103614	PmTlAg₂	mp-862966
33	Ba₂Ca₃Tl₂(CuO₃)₄	mp-556733	CaNb₂Bi₂O₉	mp-555616	Rb₂LaAuCl₆	mp-1113498
34	La₂B₃Br	mp-568985	Ce₂In₈Ir	mp-1207157	VAg₃HgO₄	mp-1216423
35	BaTl(SbO₃)₂	mvc-10727	Tc₆BiO₁₈	mp-1101632	In₂SnHg	mp-1097125
36	Sr₁₀Cu₅Bi₁₀O₂₉	mp-652781	Sb₃Au	mp-1219474	PrBiPd₂	mp-976884
37	Ba₂Tl₂Zn₂Cr₃O₁₀	mvc-3164	Sr₄LaCl₁₁	mp-1218463	TlIn₃	mp-1216611
38	Ba₂Ca₂Tl₂Fe₃O₁₀	mvc-3027	LaBiS₂O	mp-1078328	Cd₂AgPt	mp-1096169
39	Ba₂Ti₃Tl₂O₁₀	mvc-2939	HfNb₄CN₄	mp-1224363	Rb₂CeAuCl₆	mp-1113397
40	Sr₂TaAlCu₂O₇	mp-1251503	MoN	mp-1078389	In₂SnPb	mp-1223808
41	Ba₂Mg₃Tl₂(SnO₃)₄	mvc-10576	YZnGe	mp-13160	Cd₂AgPt	mp-1183537
42	Sr₂AlTlCo₂O₇	mp-1252241	Pr₃(Al₂Si₃)₂	mp-571302	Ag₂PdAu	mp-1096329
43	Ba₂AlTlV₂O₇	mp-1265780	Sr₂(BiPd)₃	mp-1207133	Ag₃AuS₂	mp-34982
44	Ba₂CaTl₂(CuO₄)₂	mp-6885	Na₃HoTi₂Nb₂O₁₂	mp-676988	PmRh₂Pb	mp-862958
45	Sr₂LaCu₂(BiO₄)₂	mp-1209034	Sr₂YCu₂BiO₇	mvc-280	PmPd₂Pb	mp-862950
46	Ba₂AlTlV₂O₇	mvc-3002	Na₃DyTi₂Nb₂O₁₂	mp-689927	Sr₂PrTlCu₂O₇	mp-1208792
47	Ba₂Mg₃Tl₂(FeO₃)₄	mvc-28	Rb₃NaRe₂O₉	mp-1209462	InAg₂Au	mp-1093943
48	Sr₂DyCu₂(BiO₄)₂	mp-1209149	Sr₃Fe₂Ag₂S₂O₅	mp-1208725	Ag₂SnBiS₄	mp-1229127
49	Ba₂CuHgO₄	mp-6562	Ba₂Pr(CuO₂)₃	mp-1228546	Sb₃Au	mp-29665
50	Ba₂Tl₂W₃O₁₀	mvc-3144	Ce₃(Al₂Si₃)₂	mp-29113	PmAg₂Pb	mp-862876

We compare the top-50 neighbours of the Hg-1223 superconductor obtained by using our embedding and two hand-crafted descriptors (Ewald sum matrix and sine Coulomb matrix) [22]. The query material, Hg-1223 (HgBa₂Ca₂Cu₃O₈), has the highest known $T_\mathrm{c}$ (134âK) at ambient pressure. Quite impressively, the neighbour list obtained by our embedding seems to be completely filled with superconductors, including the well-known Hg-1224 (No. 1) and Hg-1212 (No. 2) as well as Tl-based high- $T_\mathrm{c}$ superconductors such as Tl-2234 (No. 8), Tl-1234 (No. 32), and Tl-2212 (No. 44). By contrast, the lists obtained by the two existing descriptors contain irrelevant materials rather than superconductors. These results clearly show that our approach captures the conceptual similarity between superconductors, which is undetectable by the existing descriptors. See also the SI (appendix A3) for the detailed procedures of the descriptor computations and more discussions.

Table 2.Â The top-50 neighbours of LiCoO₂ in comparison with hand-crafted descriptors.

Â	Our embedding		Ewald sum matrix		Sine Coulomb matrix
No.	Formula	ID	Formula	ID	Formula	ID
Query	LiCoO₂	mp-22526	LiCoO₂	mp-22526	LiCoO₂	mp-22526
1	Li₁₄MgCo₁₃O₂₈	mp-769537	LiNiO₂	mp-25587	LiCoO₂	mp-1222334
2	Li₄Co₃NiO₈	mp-867537	Co(HO)₂	mp-24105	CoHO₂	mp-27913
3	Li₃Fe(CoO₃)₂	mp-761602	LiFeO₂	mp-1222302	LiCoF₂	mp-1097040
4	Li₃(CoO₂)₄	mp-850808	LiNiO₂	mp-25316	LiCoN	mp-1246462
5	Li₃MnCo₃O₈	mp-774219	Li₂NiO₂	mp-19183	Li₂CoN₂	mp-1247124
6	Li₂₀(CoO₂)₂₁	mp-532301	MgMnN₂	mp-1247154	Be₅Co	mp-1071690
7	Li₃CrCo₃O₈	mp-849768	Li₂CaCd	mp-1096283	Be₃Co	mp-1183423
8	Li₃MnCo₃O₈	mp-758163	NiO₂	mp-25210	Be₂Co	mp-1227342
9	Li₈FeCo₉O₂₀	mp-764865	LiFeOF	mp-775022	CoCN	mp-1245659
10	Li₃Co₂NiO₆	mp-765538	MnO₂	mp-1221542	Li₃Co	mp-976017
11	Li₃CrCo₃O₈	mp-759149	Co(HO)₂	mp-625939	Li₂CoO₂	mp-755133
12	Li₃TiCo₃O₈	mp-757214	Co(HO)₂	mp-625943	Li₂CoO₂	mp-755297
13	Li₄MgCo₃O₈	mp-754576	Li₂CuO₂	mp-1239022	Be₁₂Co	mp-1104193
14	Li₅Co₂Ni₃O₁₀	mp-769553	CoO₂	mp-1062939	CoO₂	mp-1181781
15	Li(CoO₂)₂	mp-552024	NaCoO₂	mp-1221066	CoO₂	mvc-13108
16	Li₁₄Co₁₃O₂₈	mp-777836	NiO₂	mp-634706	Co(HO)₂	mp-626708
17	Li₃(NiO₂)₅	mp-762165	MgMnO₂	mp-1080243	Co(HO)₂	mp-625939
18	Li₂CoO₂F	mp-764063	LiCuF₂	mp-753098	Co(HO)₂	mp-625943
19	Li₂(CoO₂)₃	mp-758539	Ni(HO)₂	mp-625074	Co(HO)₂	mp-24105
20	Li₅Fe₂Co₃O₁₀	mp-769566	CrO₂	mp-1009555	CoO₂	mp-1062939
21	Li₂CoNi₃O₈	mp-752703	CoHO₂	mp-27913	CoO₂	mp-1062643
22	Li₁₀Fe₃Co₇O₂₀	mp-760848	NaLi₂As	mp-1014873	CoO₂	mp-556750
23	Li₇Co₅O₁₂	mp-771155	LiNiO₂	mp-25411	CoH₃	mp-1183678
24	Li₃(NiO₂)₄	mp-755972	Li₂CoO₂	mp-755133	CoH	mp-1206874
25	Li₉Ni₁₅O₂₈	mp-759153	LiCuO₂	mp-754912	CoO₂	mp-1063268
26	Li₂₀Co₂₁O₄₀	mp-685270	CrN₂	mp-1014264	CoN	mp-1008985
27	Li₇(NiO₂)₁₁	mp-768079	MgCr	mp-973060	CoN	mp-1009078
28	Li₂(NiO₂)₃	mp-762391	Ni(HO)₂	mp-1180084	FeHO₂	mp-755285
29	Li₄Co₂Ni₃O₁₀	mp-778996	Co(HO)₂	mp-626708	LiFeO₂	mp-1222302
30	Li₂Co₃NiO₈	mp-757851	Ni(HO)₂	mp-27912	LiFeO₂	mp-19419
31	LiCoNiO₄	mp-754509	VO	mp-19184	CoBO₃	mp-1183397
32	Li₄(NiO₂)₇	mp-774600	Be₄AlFe	mp-1227272	LiFeOF	mp-775022
33	Li(CoO₂)₂	mp-774082	FeO₂	mp-1062652	LiNiO₂	mp-25411
34	Li(CoO₂)₂	mp-752807	LiCoF₂	mp-1097040	NiHO₂	mp-1067482
35	Li₈(NiO₂)₁₁	mp-758772	LiFeO₂	mp-19419	Li₄Co(OF)₂	mp-850355
36	Li₃CoNi₃O₈	mp-774300	Na₂NiO₂	mp-752558	NiHO₂	mp-999337
37	Li₂CoNi₃O₈	mp-1178042	Li₂CuO₂	mp-4711	LiNiO₂	mp-25587
38	Li₇(NiO₂)₈	mp-690528	Li₂CoO₂	mp-755297	LiNiO₂	mp-25316
39	Li₁₀Co₃Ni₇O₂₀	mp-769555	MgCr	mp-1185858	LiFeO₃	mp-1185320
40	Li₇Ni₁₃O₂₄	mp-758593	Sc₂CO	mp-1219429	LiFeN	mp-1245817
41	Li₉Co₇O₁₆	mp-1175506	MnBO₃	mp-1185996	CoNF₃	mp-1213745
42	Li₃Cr(CoO₃)₂	mp-761831	VN	mp-1001826	LiNiO₃	mp-1185261
43	Li₂Co₃NiO₈	mp-778768	NiHO₂	mp-999337	Li₄FeN₂	mp-28637
44	Li₂FeCo₃O₈	mp-1177976	CrO	mp-19091	LiNiN	mp-29719
45	Li₄Co₃(NiO₄)₃	mp-777850	Ni(HO)₂	mp-625072	Be₃Fe	mp-983590
46	Li₃Al₂CoO₆	mp-1222591	VN	mp-925	NiO₃	mp-1209929
47	Li(NiO₂)₂	mp-752531	GaH₆N₂F₃	mp-1224894	Be₅Fe	mp-1025010
48	LiFeO₂	mp-19419	Fe(HO)₂	mp-626680	Li₂FeO₂	mp-755094
49	Li₄AlNi₃O₈	mp-1222534	CrN	mp-1018157	Be₁₂Fe	mp-1104104
50	Li₃CoNi₃O₈	mp-757871	VN	mp-1018027	FeB₂	mp-569376

We compare the top-50 neighbours of LiCoO₂ obtained by using our embedding and two hand-crafted descriptors (Ewald sum matrix and sine Coulomb matrix) [22]. The query material, LiCoO₂, is one of the most crucial lithium-ion battery cathodes. In the list of our embedding, the many neighbours of LiCoO₂ are occupied by LiCo $_{1-{x}}$ M_xO₂ families with the same layered structure as LiCoO₂ but partly substituted with different transition metals M. Since these partial substitutions are represented as supercells, the system's apparent size is larger than the original unit cells. Our approach is unaffected by these apparent differences and can recognise the essential similarities. While most of our list is filled with lithium oxides, the other two lists obtained by the existing descriptors do not suggest this consistent trend. These results suggest that our model recognises the concept of lithium-ion battery cathodes, which is not captured by the existing descriptors. See also the SI (appendix A3) for the detailed procedures of the descriptor computations and more discussions.

Next, we examined lithium-ion battery materials, which substantially support our lives of today. This technology has been developed through the discovery of new materials and the understanding of their structure-composition-property-performance relationships and is now bottlenecked by the cathodes (positive electrodes) in terms of the energy density and production cost [5]. We therefore studied the neighbourhoods of LiCoO₂, the first yet most dominant cathode material [5]. Impressively, two of the three leading cathode material groups, namely, the layered, spinel families [5] (see figure 6(b) for visualisations), were identified in the neighbourhoods. Specifically, similar to LiCoO₂, a family of layered LiMO₂, with M being transition metals, were found within the top-10 neighbourhoods of LiCoO₂ (see table 2), including important battery materials LiNiO₂ families. Spinels as another important family were found as LiNi₂O₄ at the 51th neighbour and LiCo₂O₄ in the 200s neighbours. The polyanion family, the remaining one of three major cathode families, were not placed in the vicinity of LiCoO₂ but formed a distinctive cluster at the top edge in figure 3(a). Interestingly, all of these materials were developed by the group of Nobel laureate John Goodenough [5]. This fact suggests that the embeddings capture conceptual similarity among the battery materials that previously required one of the brightest minds of the time to be discovered.

Note that our method properly links substituted materials and the original material without being confused by ad hoc supercell expression (e.g. Li₄Co₃NiO₈ = LiCo_0.75Ni_0.25O₂). This advantage is particularly noticeable in comparison with embeddings constructed using conventional features (table 2). This result indicates that our approach can recognise the essential structural features without being affected by superficial differences (i.e. the number of atoms or the size of the unit cell).

Additionally, we analysed the vicinities of magnetic materials, including 2D ferromagnets, which are attracting much attention for their interesting properties [41], and commercial samariumâcobalt (SmâCo) permanent magnets. Again, the embeddings capture meaningful similarity in these material classes, as shown in figures 7 and 8, which is often not evident to non-specialists (see appendix A1 in the supplementary information (SI) for more discussions and detailed results).

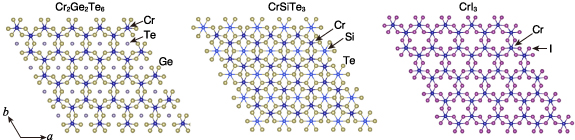
Figure 7. Refer to the following caption and surrounding text. — **Figure 7.**Â Crystal structures of the 2D ferromagnet Cr₂Ge₂Te₆ and its neighbours in the embedding space. The double discoveries of 2D ferromagnets in 2017, after long questioning their existence, are gathering great interest from the magnetic materials community [41]. When we analysed the neighbourhoods of one of these 2D ferromagnets, Cr₂Ge₂Te₆ (mp-541449), our embedding space successfully captured CrSiTe₃ (mp-3779), a compound known as a potentially 2D-ferromagnetic insulator, as the first neighbour and even the other 2D ferromagnet CrI₃ (mp-1213805) as the 15th neighbours among 122â543 materials. More detailed results and discussions are given in the SI (appendix A1).
Download figure:
Standard image High-resolution image

Figure 8. Refer to the following caption and surrounding text. — **Figure 8.**Â Crystal structures of the Sm₂Co₁₇ permanent magnet and its neighbours in the embedding space. Here we highlight two compounds in the neighbourhood list of Sm₂Co₁₇: SmCo₅ and SmCo₁₂. Sm₂Co₁₇ and SmCo₅ are the two major components in SmâCo magnets often used in high-temperature environment, whereas SmCo₁₂ is one of the compounds with the so-called 1â12 structure that has been drawing attention for its potential for permanent magnets. In the neighbourhoods of Sm₂Co₁₇ (mp-1200096) in our embedding space, we found SmCo₁₂ (mp-1094061) as the 255th neighbour and SmCo₅ (mp-1429) around the top 0.5% neighbourhoods. It is well known in the community that the crystal structures of Sm₂Co₁₇, SmCo₅, and SmCo₁₂ have close connections with each other [4]. However, without the literature context and proper visualisation, it is difficult for a human analyst to recognise these connections. More detailed results and discussions are given in the SI (appendix A1).
Download figure:
Standard image High-resolution image

These in-depth analyses across diverse materials consistently support the conclusion that our ML model recognises similar functionalities of materials behind different structures without being explicitly taught to do so. We anticipate that when a material with beneficial properties is found, we may be able to screen for new promising candidates based on the conceptual similarities captured in this embedding space.

2.3.Â Performance validation as a materials descriptor

Here we provide quantitative insight into characteristics of embeddings. Particularly, we analyse the performance of predicting material properties using trained embeddings as input. As we are more interested in predicting functional material properties, we conducted a binary classification task of materials concepts, in which an ML model predicts whether a material belongs to a particular material class or not.

We expect that our embeddings contain the information of materials concepts. If so, we can rapidly screen materials with a desired concept from a material database by combining the embeddings with an ML model. However, properly labelling materials with their concepts requires experiments or consideration by experts, and thus the number of available labelled data for a given concept is likely to be limited. Therefore, as a benchmark and a use case for our embeddings, we evaluated the materials concept classification in the settings of few training data.

As benchmark materials, we used superconductors and thermoelectric materials for their complex and interesting properties. We used the Crystallography Open Database (COD) as the data source. The number of positive data used for training was 469 for superconductors and 286 for thermoelectric materials. Embeddings of these materials were obtained by the crystal structure encoder trained on the MP dataset via deep metric learning, and were used as input to a random forest classifier. As a baseline for comparison, we used latent feature vectors of crystal graph convolutional neural network (CGCNN) trained for total energy prediction, as in appendix C. We evaluated the prediction performance with leave-p-groups-out cross-validation while varying the training data size. Here, both the training and testing splits were made to contain balanced positive and negative samples.

As shown in figure 9, the classifier using our embeddings obtained good classification performance for both superconductors and thermoelectric materials. In particular, when the number of training data is very small (around 10), our method shows significantly better performance than the baseline. We will more discuss these results in the next section.

Figure 9. Refer to the following caption and surrounding text. — **Figure 9.**Â The prediction performance of materials concepts. For superconductors and thermoelectric materials, embeddings obtained by our DML approach show higher performance especially when the size of the training dataset is very small. The embeddings of the baseline were latent vectors of CGCNN trained to predict total energy from crystal structures, as done by Xie *et al* [12].
Download figure:
Standard image High-resolution image

3.Â Discussions

As assumed, materials concepts were exposed spontaneously in an abstract space. As we confirmed in the numerical evaluations of the training task of metric learning (appendix B in SI), this space was shown to successfully unify the two complementary factors of crystal structures. We hypothesise that these remarkable properties of our embeddings were made possible by the following two key features of our method that are distinctive from the existing material embedding methods [25â29]. First, we used deep metric learning, which directly optimises the spatial arrangements of the embedding vectors via a loss in terms of the Euclidean distances between them. This procedure is critically different from the existing methods [25â29], which learn embeddings indirectly as DNN's latent vectors. Although these latent vectors should encode essential information about materials, the explicit metric optimisation of embeddings is equally important for map creation and similarity learning. Second, our self-supervised learning is enabled by exploiting two forms of inputs expressing complementary structural characteristics: a set of atoms in the unit cell with their connections as the local characteristics and the XRD pattern, which is essentially a Fourier transformed crystal structure [1], as the periodic characteristics. Representation learning is known to be generally more well-informed when diverse multi-modal data are used for training [44]. In contrast to approaches that rely on single forms of materials data expression [25â29], our model benefits from learning across two forms of expression, or cross-modal learning.

The results of the materials concept classification (figure 9) clearly support these hypotheses. Remind that the baseline method (CGCNN [12]) learns embeddings as latent vectors in a DNN with only crystal structures as input, whereas our method uses the same DNN but trains it along with another DNN for XRD patterns in cross-modal deep metric learning. Thus, the performance advantage of our method directly indicates the benefit of the proposed cross-modal deep metric learning approach. We believe that our method using both crystal structures and XRD patterns helped the ML model to capture local motifs and lattice more effectively, which contributed to better learning of structural patterns correlated to material functionality and thus better recognition of materials concepts. We expect that incorporating more diverse structure representations of materials such as electronic structure into our multi-modal learning framework will further benefit the representation learning of materials. We leave such extensions as future work.

To provide more insight into the difference between our method and the baseline (CGCNN), we further analysed the performance of these methods for physical property prediction (see appendix C in SI for details). Similarly to the materials concept classification, we trained random forest models to predict materials properties, such as total energy, space group, and density, from learned embeddings. Our embedding outperformed the baseline in predicting density and space group and performed comparably in total energy and magnetisation (figure S1 in SI). This result confirms that our embeddings indeed capture lattice information in crystal structures more effectively than the single-modal baseline using only crystal structures. Performing comparably in total energy prediction is also notable, because the embeddings of the baseline are trained to specifically predict total energy itself using rich supervision from density functional theory calculations while our embeddings are not.

A major interest in the proposed method given its good predictive power is whether it has potential utility for new material discovery. To investigate such possibilities, we conducted a simple test to see if our model can re-discover superconductors known in the literature but not included in the training dataset. To this end, we borrowed the COD's superconductors from the concept classification (figure 9) and, after removing overlaps with the MP's training dataset, we mapped their embeddings in the MP's embedding distribution presented in figure 3. As shown in appendix E, these COD's superconductors are most intensively concentrated around the superconductor cluster in the MP's training materials, despite the fact that these COD's materials are novel to the model. This result suggests a screen method of new candidate materials by using our model trained on a database of known materials.

Another notable strength of our method over existing material embedding methods is that it does not require costly annotations and can be trained using only primitive structural information (i.e. crystal structures and their XRD patterns). This makes our method applicable to a wide range of datasets. Even when annotations are available, our self-supervised approach will benefit many users as a means of pre-training. Pre-training is a general ML technique performed on a large-scale dataset to help an ML model for other tasks where annotated training data are limited [45]. Our self-supervised learning is suitable for this purpose, because it can be performed given only crystal structure data and can thus utilise various material databases at scale.

When compared to classic material descriptors such as the Coulomb matrix variants [22], our method has advantages in terms of its scalability and ability to capture high-level material properties. See tables 1, 2 and the SI (appendix A3) for analysis results and more discussions.

Since the focus of our study was on learning material similarity from unannotated structural data, the resulting map requires manually interpreting clusters on the basis of our knowledge of materials concepts. Interestingly, a word2vec model [26] has been applied to text symbols appearing in the materials science literature, thus learning relationships such as the connections between 'Fe' and 'metal' and between 'SmâCo' and 'magnet'. Use of this technique may further automate the interpretation of our results with literal knowledge.

4.Â Conclusions and broader impacts

In summary, we have demonstrated the self-supervised learning of material embeddings solely from crystal structures using DNNs. Careful inspection of the embedding space, in terms of both the global distribution and local neighbourhoods, has confirmed that the space recognises functionality-level material similarity or materials concepts. Our techniques for the materials space visualisation and the similarity evaluation between crystal structures will be useful for discovering new underlying relationships among materials and screening for new promising material candidates. Since these techniques are not strongly affected by human bias, they could give rise to a new view of materials that can stimulate efforts to break through our knowledge barriers.

Our result is also applicable to material retrieval systems that can search for conceptually similar materials in a database given a query material. This approach will enable us to rediscover materials that have never been recognised to have preferable properties.

Furthermore, constructing a functionality-aware representation space of crystal structures is a first step towards the inverse design of materials [8, 46], a grand challenge of materials informatics. This workflow would allow us to design materials in the functionality space and inversely map the functionality attributes to synthesisable crystal structures with the desired properties. We hope that this study will pave the way for breakthroughs in the ML-assisted discovery and design of materials.

5.Â Methods

5.1.Â Data acquisition and pre-processing

We used the Materials Project as the data source for this study. We collected data for up to quintet systems, excluding monatomic crystals, on 8 July 2020, using the Material Project APIs, which resulted in a total of 122â543 materials (93% of the source collection) as our targets. We additionally queried thermodynamic stability material attributes on 14 October 2020. We used VESTA [47] for crystal structure visualisation. We calculated the XRD patterns using pymatgen [48]. The x-ray wavelength was set to 1.54â184âÃ (Cu K $_{\alpha 1}$ ), and the 2Î¸ angle ranged from 10^â to 110^â with a step size of 0.02^â; thus, 5000-dimensional vectors of 1D-structured XRD patterns were produced. To ease the learning process, the intensity scale of each XRD pattern was normalised by setting the maximum intensity to 1.

5.2.Â Neural network architecture

As illustrated in figure 2(a), we used two types of DNNs as embedding encoders. For the crystal-structure encoding, we need to convert a set of arbitrary number of atoms (i.e. the atoms in the unit cell) into a fixed-size embedding vector in a fashion invariant to the permutation of atom indices. For this purpose, we used CGCNNs [12]. As input to CGCNN, the 3D point cloud of the atoms in the unit cell is transformed into a graph of atoms whose edge connections are defined by their neighbours within a radius of 8âÃ. The atoms in the graph are represented as atom feature vectors and are transformed into a single fixed-size feature vector via three graph convolution layers and a global pooling layer. For the XRD patterns, we used a standard feed-forward 1D convolutional neural network designed following existing studies on XRD pattern encoding [49]. At the end of each network, we used three fully connected layers to output 1024-dimensional embedding vectors. Since one of these encoders is supervised by the output of the other in our self-supervised learning approach, training them simultaneously tends to be unstable compared to standard supervised learning. To stabilise the training process, we found that batch normalisation [50] is essential after every convolutional/linear layer in both networks except for the final linear output layers. We discuss this further in the SI (appendix B). Further details of our network architecture are provided in the SI (tables S6 and S7 in appendix D) and our ML model codes.

5.3.Â Training procedures

In each training iteration, we processed a batch of N input material samples. Let x _i and y _i be a pair of embedding vectors produced for the ith crystal structure in a batch and its XRD pattern, respectively. For each positive pair $(\boldsymbol{x}_i, \boldsymbol{y}_i)$ , we randomly drew two kinds of negative samples $\boldsymbol{x}^{^{\prime}}_i$ and $\boldsymbol{y}^{^{\prime}}_i$ , representing a crystal structure and an XRD pattern, respectively, from the batch to form two triplet losses:

$\begin{align} L_{nx}^{(i)}(\boldsymbol{x}_{i}, \boldsymbol{y}_{i}, \boldsymbol{x}^{^{\prime}}_{i}) & = \mathrm{max}(0, \|\boldsymbol{x}_{i}-\boldsymbol{y}_{i}\| - \|\boldsymbol{x}^{^{\prime}}_{i}-\boldsymbol{y}_{i}\| + m), \end{align} \tag{ 1 }$

$\begin{align} L_{ny}^{(i)}(\boldsymbol{x}_{i}, \boldsymbol{y}_{i}, \boldsymbol{y}^{^{\prime}}_{i}) & = \mathrm{max}(0, \|\boldsymbol{x}_{i}-\boldsymbol{y}_{i}\| - \|\boldsymbol{x}_{i}-\boldsymbol{y}^{^{\prime}}_{i}\| + m), \end{align} \tag{ 2 }$

where the negative sample $\boldsymbol{x}^{^{\prime}}_{i}$ was chosen from $\{\boldsymbol{x}_k\}_{k\neq i}$ to produce a positive-valued loss, $L_{nx}^{(i)} \gt 0$ , and $\boldsymbol{y}^{^{\prime}}_{i}$ was chosen similarly from $\{\boldsymbol{y}_k\}_{k\neq i}$ (see also figure 2(b) for illustrations). Here, mâ>â0 is a hyperparameter called the margin. Equation (1) essentially requires that for each embedding y _i, its negative samples $\boldsymbol{x}^{^{\prime}}_{i}$ are cleared out of the area surrounding y _i having the radius of the positive-pair distance $\|\boldsymbol{x}_{i}-\boldsymbol{y}_{i}\|$ (red circle in the top-right part of figure 2(b) plus the margin m (yellow area in the figure). Equation (2) is defined similarly. These losses are thus to ensure, given an embedding as a query, that its paired embedding is retrievable as the query's nearest neighbour. Note that the choice of the margin m is quite flexible because its value is relevant only to the scales of the embeddings, which are unnormalised and arbitrarily learnable. Here, m = 1. Our bidirectional triplet loss was then computed as the average of the losses for all samples in the batch as follows:

$\begin{equation} L = \frac{1}{2N}\sum_{i = 1}^N (L_{nx}^{(i)} + L_{ny}^{(i)}). \end{equation} \tag{ 3 }$

This expression is similar to but simpler in form than a loss expression previously used in cross-modal retrieval [51].

We optimised the loss function using stochastic gradient descent with a batch size N equal to 512. Using the Adam optimiser [52] with a constant learning rate of 10^â3, we conducted iterative training for a total of 1000 epochs for all target materials in the dataset. The training took approximately one day using a single NVIDIA V100 GPU. For details regarding our strategies for validating the trained models and tuning the hyperparameters (e.g. choices of the embedding dimensionality and training batch-size), see appendix B and table S5 in the SI.

5.4.Â Data acquisition for the concept classification tasks

For the materials concept classification, we collected the crystal structure data of superconductors and thermoelectric materials from COD. To collect positive samples for each category, we retrieved material entries containing certain keywords in their paper titles as positive samples. Specifically, the entries including 'superconductor' or 'superconductivity' in their titles were regarded as superconductors, and the entries including 'thermoelectric' or 'thermoelectricity' were regarded as thermoelectric materials. The same number of material entries without these keywords were randomly collected and used as negative samples.

Acknowledgment

This work is partly supported by JST-Mirai Program, Grant Nos. JPMJMI21G2 and JPMJMI19G1. Y S is supported by JST ACT-I Grant Number JPMJPR18UE.

Data availability statement

The materials data retrieved from the Materials Project, the trained embeddings of these materials, and the trained ML model weights are available at the figshare repository [53]. The list of the target materials used in this study, the lists of the neighbourhood search results, and interactive web pages for exploring the materials map visualisation and analysing local neighbourhoods are available in the GitHub repository (https://github.com/quantumbeam/materials-concept-learning).

Author contributions

Y S, Y U, and K O conceived the idea for the present work. Y S and T T carried out the numerical experiments. All authors discussed the results and wrote the manuscript together.

Competing interests

The authors declare no conflicts of interest associated with this manuscri.

Author e-mails

Author affiliations

Author notes

ORCID iDs

Dates

Peer review information