Evaluation of interpretability methods for multivariate time series forecasting

Abstract

Being able to interpret a model’s predictions is a crucial task in many machine learning applications. Specifically, local interpretability is important in determining why a model makes particular predictions. Despite the recent focus on interpretable Artificial Intelligence (AI), there have been few studies on local interpretability methods for time series forecasting, while existing approaches mainly focus on time series classification tasks. In this study, we propose two novel evaluation metrics for time series forecasting: Area Over the Perturbation Curve for Regression and Ablation Percentage Threshold. These two metrics can measure the local fidelity of local explanation methods. We extend the theoretical foundation to collect experimental results on four popular datasets. Both metrics enable a comprehensive comparison of numerous local explanation methods, and an intuitive approach to interpret model predictions. Lastly, we provide heuristical reasoning for this analysis through an extensive numerical study.

1 Introduction

As machine learning approaches become increasingly capable and find more use cases in the society, machine learning systems get more complex and less interpretable. The typical approach to assess the model performance is to measure the prediction performance (e.g. by mean squared error and mean absolute error for regression tasks) over a test set which does not consider the interpretability of the underlying model. In the absence of an understanding about why a model is making a decision, trusting a model can lead to inaccurate and potentially dangerous decisions [5]. However, in recent years, the value of interpretability in machine learning has been recognized and gained significant attention [1, 8, 14].

Higher interpretability has many benefits. First of all, it can create trust by showing the different factors contributing to the decisions [12]. Trust on the model in turn can lead to a higher acceptance of machine learning systems [1]. Secondly, interpretability tools can reveal incompleteness in the problem formalization [8]. This information can then be used for debugging purposes, and designing better models. Finally, interpretability methods can be used to improve our scientific understanding [8]. By analyzing how machine learning models behave, we can enhance knowledge about the subject matter [3].

Interpretability aims to better understand a black-box model. Based on the scope of interpretability, we can divide existing methods to two classes: global and local. Global interpretability methods aim to explain the entire logic and reasoning of a model. On the other hand, local interpretability methods focus on explaining the reasons for a specific decision [1].

Considering the large number of real-world applications of multivariate time series forecasting models in areas such as retail, medicine and economics, increased interpretability of those models can have significant practical implications. The majority of the works on this topic focuses on computing (temporal) variable importance to gain insights about datasets and models [22]. The variable importances can be used for feature selection [27] and model compression [16]. For instance, the temporal variable importances can help identifying which temporal features are more important to the prediction model [15]. The two-sided local explanation methods that are considered in this paper (e.g., SHAP (Shapley Additive Explanations) [23]) can further demistify the prediction process. The local explanations provided by these methods can be positive or negative depending on how the features are affecting the predicted value whereas the variable importance methods only measure a single positive value which is indicative of the importance, not contribution of the feature. For instance, Mokhtari et al. [29] use SHAP to interpret financial time series models, where the contribution scores provided by SHAP allow financial experts to better understand the model’s decisions.

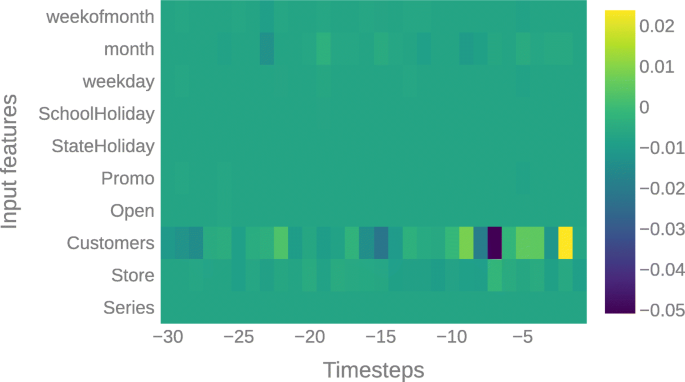
In this paper, we focus on local explanations for multivariate time series forecasting, where multivariate refers to multiple input features. For a selected sample and forecasting horizon, a local explanation method can be used to show the contribution of each input feature to the prediction. Local explanations are two-sided which means that they show both the magnitude and the directional importance. A heatmap of feature importances for an arbitrary sample in the Rossmann sales dataset is provided in Fig. 1, which shows the positively and negatively contributing features in yellow and blue, respectively. The Rossmann sales dataset consists of the historical store sales of more than a thousand drug stores. All samples from the dataset contain a 30 day time window (x-axis) of 10 different features (y-axis). By analyzing local explanations over the samples, we can observe how important different features are to the model and how they are contributing to the prediction. For instance, from Figure 1, it can be inferred that the number of customers is the most important feature for the local predictions (i.e., for the illustrated sample). We can observe that the more recent values of the customers feature have greater contribution to the prediction than the older values for this particular time window. Furthermore, examining the local explanations for certain scenarios such as promotions can provide insights about how the complex prediction model makes decisions. These feature importances can also be averaged over many samples to compute the global importance of each feature.

Fig. 1

Local explanation of a random sample from the Rossmann dataset obtained from feature importances, where the positively and negatively contributing features are highlighted in yellow and blue, respectively. This sample shows that the number of customers is the most important feature for the local predictions

Evaluation of local explanations is challenging but necessary to minimize misleading explanations. Various approaches have been used to evaluate local explanations, from visual inspection [7] to measuring the impact of deleting important features on the classifier output [34, 37]. In time series forecasting domain, there are only a few studies focusing on interpretability of machine learning models [36, 44]. Moreover, the literature mostly focuses on the time series classification task [33]. On the other hand, the research on interpretability of time series regression models mainly focuses on intrinsic explainability [22], and the absence of proper evaluation metrics for local explanation methods can be deemed as one possible reason for the lack of studies on interpreting time series regression models. Interpreting time series regression models is equally important to those of time series classification, as these are highly relevant in many areas including electricity load [32] and wind speed [31] forecasting, anomaly detection [35], spectrum occupancy prediction [38], sales forecasting [20], and more recently, for COVID-19 spread forecasting [11, 18]. Considering the large number of real-world applications, increased interpretability of these models can be highly important for practitioners in many domains. In this regard, our paper makes the following contributions:

• Novel evaluation metrics for time series regression: We introduce two novel evaluation metrics for comparing local interpretability methods which can be applied on any type of time series regression problems.

• Comparison of local explanation methods for multivariate time series regression: We perform a comprehensive comparison of three local explanation approaches (and a random baseline) on four different datasets.

The remainder of the paper is organized as follows. Section 2 provides discussion on the interpretability methods for time series models, feature selection methods, and evaluation of local explanations. Section 3 describes the datasets, the forecasting models and the local explanation methods used in our analysis. Section 4 presents the results and the insights obtained from the numerical study. Finally, Section 5 provides concluding remarks along with future research directions.

2 Related work

Machine learning has been used to improve many products and processes. On the other hand, a large barrier for adopting machine learning in many systems has been the black-box architecture of many machine learning systems, which prompted a large number of studies on AI interpretability in recent years [30].

Interpretable AI can be considered as a toolbox that consists of many different strategies. While different taxonomies were proposed, we focus on the one proposed by Adadi and Berrada [1] where the existing interpretable AI approaches are classified under three criteria: complexity, scope and model-related.

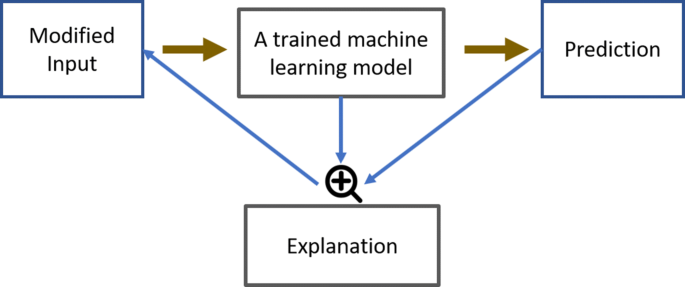
In terms of complexity, generally, a more complex model is more difficult to interpret and explain [1]. The simplest approach for interpretability is to use an intrinsically explainable model that is considered interpretable due to its simple structure, e.g., a decision tree. However, these models usually do not perform as well as the more complex ones, which lends credibility to the argument that intrinsic explainability comes with a reduction in prediction performance. An alternative approach to interpretability is post-hoc interpretability, which is illustrated in Fig. 2. In this approach, the explanation is generated after model training. Most post-hoc interpretability methods work by creating perturbations in the input. Then, the method observes the model outputs for the modified inputs. In some cases, the interpretability method can also access to the model internals such as the weights of a neural network. Finally, the interpretability model uses the predictions and the model internals to reverse engineer the process and generate an explanation. The trade-off between the accuracy and the explanation fidelity is the crucial difference between the instrinsic and post-hoc interpretability methods. Intrinsically explainable models can sacrifice prediction performance to provide accurate and undistorted explanations. On the other hand, post-hoc methods are limited in their capacity to approximate the predictions of a complex model.

Fig. 2

Post-hoc interpretability approach. The explanation method feeds modified input to the trained model, and the model predictions are used along with model internals to reverse engineer the process

Although this approach might be computationally expensive, post-hoc interpretability methods are typically model-agnostic and many recent studies on interpretable AI falls under this category [33, 36, 37].

In terms of scope, we focus on local interpretability methods since they give a more detailed picture of the model behavior. For some models, local explanations are relatively easy to construct. For instance, in a Naive Bayes classifier, we can use the class probabilities with respect to each feature, and for a decision tree, we can use the path chosen as the explanation. However, when there are many features, even these models become increasingly complex and not interpretable. Thus, post-hoc interpretability methods such as LIME [40] and SHAP [23] can be used to explain decisions of a model.

Another way to categorize interpretable AI methods is based on whether they are model specific or model agnostic. Model agnostic methods are usually preferable as they can be applied to all types of machine learning models. However, model specific methods can use inherent properties of a machine learning model, and can be computationally cheaper. Lundberg and Lee [23] developed different SHAP algorithms for post-hoc interpretability. While the proposed kernelSHAP method can be considered as a model agnostic interpretability method, the authors also proposed two faster model-specific approximations of the same approach for neural networks and tree-based models.

In the case of a large number of features, high-dimensionality of the data might pose a problem as the samples appear equidistant from each other. In such situations, various feature selection methods can be used to filter out some of the features which can result in accuracy and speed improvements. Feature selection methods can be divided into three categories: filter, wrapper, and embedded. The filter methods determine the important features only by looking at the dataset, not the model. The Pearson correlation coefficient and Mutual Information (MI) are the two commonly used filter-based feature selection methods. These methods are usually fast, however, they can only detect linear dependencies between the features and the models’ output, and they do not take into account feature interactions [6]. Wrapper methods evaluate subsets of features, which allows them to detect possible interactions among variables. On the other hand, these methods are computationally expensive, and heuristics are usually applied to reduce the computation time. Local explanation methods can also be used as a wrapper feature selection method. Marcílio and Eler [27] test the SHAP method on high-dimensional UCI datasets, and find that it achieves better results compared to three commonly used feature selection algorithms. Lastly, embedded methods aim to combine the advantages of both previous methods by performing feature selection and prediction at the same time. They find the best features during training, which makes them model-specific. These methods can use mutual information or model parameters to find the feature importance and perform feature selection. For example, different decision tree criteria can be used to perform feature selection for decision tree models [13]. In neural network-based models, pruning strategies can be applied to remove insignificant node connections with very small weights [17].

Various approaches have been suggested to interpret and understand the behavior of time series models. We focus on post-hoc local explanation methods due to their more detailed explanations and ease of use. Perturbation-based approaches measure the feature importance by replacing the input features with different values and observing the change in the output without any knowledge of the model parameters. These methods assign higher feature importance to a feature which has the highest impact on the output when removed. For time series prediction, how to represent a removed feature can be tricky: replacement with mean value and adding random noise are two popular options [9]. Attribution methods explain models by computing the contribution of each input feature to the prediction. Attributions can be assigned using gradient-based methods by measuring the change in the output caused by changes in the input features [42]. SHAP [23] is an attribution based method and has been previously considered for time series classification [33].

Evaluation of local explanations remain largely unexplored for time series forecasting models. Even though it is studied for computer vision [9] and natural language [34], these methods cannot be directly applied to time series prediction. In this paper, we propose two new evaluation metrics that can be applied to all types of time series forecasting models.

3 Methodology

In this section, we describe the datasets, the forecasting models and the local explanation methods used in our analysis.

3.1 Datasets

We experiment with four multivariate time series datasets whose characteristics are summarized in Table 1. We add time covariates as features to the datasets with periodic behavior to improve the prediction performance. We apply min-max normalization on the target feature in all the datasets to bound the output feature between 0 and 1. To maintain generalizability, we use a representative set of 100 randomly selected time series from the Electricity, Rossmann and Walmart datasets to train the machine learning models, whereas we use all six time series (i.e., subjects) from the Ohio dataset.

• Electricity: This dataset contains the hourly electricity consumption of 370 households in total, and has been used as a benchmark for many time series forecasting models [22, 41]. In addition to two available features in the dataset (hourly electricity consumption and house id), we generate four covariates (hour of the day, day of the week, week of the month, and month) to be included in our analysis.

• Rossmann: The Rossmann store sales dataset is released as part of a Kaggle competition in 2015.¹ This is the first competition where a neural network placed in the top three for a time series forecasting task [2]. The neural network submission uses a global fully connected neural network with the exogenous variables provided in the competition. The dataset contains sales data from 1,115 Rossmann stores, providing a useful test bed for sales forecasting tasks. The dataset contains eight features (store number, sales, customers, open, promo, state holiday, school holiday and day of week). In our analysis, we include two additional time covariates, which are week of the month and month.

• Walmart: The Walmart store sales forecasting dataset is released as part of a Kaggle competition in 2014.² The dataset contains weekly store sales of 45 stores and 77 departments. Multiple exogenous variables such as temperature, fuel prices, CPI, unemployment, and information on markdowns are available in the dataset. The top performing solutions of the Kaggle competition uses conventional time series methods with minor tweaks which indicates that accurate modelling of the seasonality and holiday patterns are very important.

  Many forecasting models do not employ majority of the exogenous variables including temperature, fuel prices, CPI, unemployment and markdown since they do not sufficiently improve the forecasting performance [2]. The processed version of the dataset used in our analysis contains ten features: Weekly Sales, Store Size, Store Type, Temperature, Store Id, Department Id, day, week of month, month, and year.

• Ohio: The OhioT1DM [28] dataset contains 8 weeks worth of data collected from 6 type-1 diabetic patients in 5 minute intervals. We use this dataset for the glucose forecasting task, which involves three continuous features (Glucose level, insulin level and CHO intake) and one discrete feature (Subject).

Table 1 Dataset specifications

3.2 Time series forecasting models

We consider three different machine learning models for time series forecasting: Time Delay Neural Network (TDNN) [46], Long Short Term Memory Network (LSTM) [19], and Gradient Boosted Regressor (GBR) [10]. We note that there are various other machine learning-based time series forecasting methods, and we choose these three (TDNN, LSTM, and GBR) as representative models. We refer the reader to recent forecasting competitions for more information on best performing time series forecasting methods [2, 25, 26]. There are various strategies for training these models for time series forecasting [45]. Typically, the multiple input multiple output (MIMO) strategy is used for training the Neural Network models where a single model is trained to predict multiple forecasting horizons. The MIMO strategy is not directly applicable to GBR, and we use a direct strategy for GBR where a separate model is trained to predict each step in the forecasting horizon.

3.2.1 Time delay neural network (TDNN)

This neural network architecture is composed of an input layer, a set of hidden layers and an output layer. The topology of the network architecture is a feedforward neural network. In a typical TDNN, a sigmoid activation is used for each hidden unit, and a dropout layer can be added after each hidden layer in the network. In our implementation, we randomly initialize all the weights in the network to be close to 0. Furthermore, we use Root Mean Squared Error (RMSE) as our evaluation metric for the loss function, and Adam optimizer [21] for backpropagation.

3.2.2 Long short term memory network (LSTM)

LSTM networks are very popular in the literature for time series analysis. They can capture long term dependencies in sequential data, which is an important advantage over TDNNs. LSTMs are a special type of Recurrent Neural Networks; unlike TDNNs they are optimized using backpropagation through time, which unrolls the neural network and backpropagates the error through the entire input sequence. This process can be slow, however, it allows the network to take advantage of the temporal dependencies between the observations.

Multiple LSTMs can be stacked to create a stacked LSTM network. In stacked LSTMs, the hidden state of the early LSTM layer is fed as an input to the following LSTM layer. This approach can be useful as it allows hidden states at different layers to operate at different time scales [39]. Dropout can be applied after each LSTM layer in a stacked LSTM. We use a multi-layer stacked LSTM network for the time series prediction task. Similar to the TDNN model, we use RMSE as the evaluation metric, and Adam optimizer for updating the weights of the network.

3.2.3 Gradient boosted regressor (GBR)

Gradient boosting is another popular model in contemporary machine learning. The simplest gradient boosting algorithm consists of learning many weak learners through functional gradient descent, and adding weak learners to a base function approximator. This is in contrast to how neural networks learn.

Neural networks have risen to prominence largely due to their universal function approximator properties. Neural networks use activation functions for nonlinear function approximation, and can be expressed in closed form as y = F(x;Θ), where Θ represents the weights in the network, x is a vector consisting of the regressor values, and y is the target vector. Gradient boosting utilizes classification and regression trees (CART) [4] instead of activation functions to achieve its non-linearity. That is,

$$ \mathbf{y} = F(\mathbf{x}; \{{\upbeta}_{m}, \mathbf{a}_{m}\}_{m=1}^{M})=\sum\limits_{m=1}^{M} {\upbeta}_{m} h\left( \mathbf{x} ; \mathbf{a}_{m}\right) $$

(1)

where $h\left (\mathbf {x} ; \mathbf {a}_{m}\right )$ represent the weak learners. In addition, the number of learners is specified by a hyper-parameter, M. By changing the atomic building block from neurons and activation functions to decision trees, several modifications are needed. Instead of performing classical gradient descent, more complicated updates are required for training. These updates are made through performing functional gradient descent, and adding these functions to the base model.

In (1), the parameters a_m represent the weights in each decision tree, and the parameter β_m represents the weight of the tree in the general model. The loss function can be chosen according to the problem specifications, where commonly used loss functions include the mean squared loss (L2), mean absolute loss (L1) and logistic loss.

In our analysis, due to the multi-step forecasting nature of the problem, we have trained numerous gradient boosting regressors, each responsible for predicting a particular forecasting horizon. We take the learning rate as 0.01, use the least squares loss for the loss function, and Friedman Mean Squared Error for the tree splitting criterion.

3.3 Local explanation methods

A particular dataset can be defined as combination of J features. Each feature j ∈{1,…,J} has a corresponding feature space, which we denote as $\mathcal {S}^{j}$, with n permissible values. That is,

$$ \begin{array}{@{}rcl@{}} \mathcal{S}^{j} \equiv \{s_{1}^{[j]}, s_{2}^{[j]}, \hdots, s_{n}^{[j]}\} = \{s_{i}^{[j]}\}_{i=1}^{n} \end{array} $$

A discrete time series model, F, can be formulated as y_t = F(X_t) + 𝜖_t, where t represents the time step. The explanatory variables are represented as X_t, the target vector is y_t, and the error in the model is 𝜖_t. The target vector y_t produces a multi-horizon forecast of length τ₀. For simplicity of notation, we only consider one of these target time horizons, at an arbitrary index τ ∈{1,…,τ₀}, in below analytical expressions.

$$ \begin{array}{@{}rcl@{}} y_{t} &\equiv& \mathbf{y_{t}}^{[\tau]} \\ &=& \mathbf{F}_{\tau}(\mathbf{X}_{t}) + \boldsymbol{\epsilon}_{t}^{[\tau]} \\ &\equiv& f(\mathbf{X}_{t}) + \epsilon_{t} \end{array} $$

We drop the index, τ, without loss of generality, and refer to this by scalar notation y_t. It is a simple extension to perform a multi-step forecast. As well, we explicitly choose to omit the time series index for notational convenience. Note that our proposed approach naturally scales to multiple time series.

We denote the explanatory variables in matrix form, to allow for a sliding window of time slices, x_t. The sliding window is of length L. This can be seen as,

$$ \begin{array}{@{}rcl@{}} \mathbf{X}_{t} &=& [\mathbf{x}_{t-(L-1)}, \mathbf{x}_{t-(L-2)}, \hdots, \mathbf{x}_{t}] \\ &=& \{ x_{j\ell,t} \}, \quad j \in \{1,\hdots,J\},\quad \ell \in \{1,\hdots,L\} \end{array} $$

where we describe an individual covariate at position (j,ℓ) in the full covariate matrix at time step t as x_jℓ,t.

We take x_t as an individual time slice. Each feature relates to its feature set, represented by a superscript. That is,

$$ \begin{array}{@{}rcl@{}} \mathbf{x}_{t} &= \left[\begin{array}{c} x_{t}^{[1]} \\ x_{t}^{[2]} \\ {\vdots} \\ x_{t}^{[J]} \end{array}\right] \end{array} $$

For example, if our sets were

$$ \begin{array}{@{}rcl@{}} \mathcal{S}^{1} &\equiv& \{\text{Apple}, \text{Banana}, \text{Tomato}\} \\ \mathcal{S}^{2} &\equiv& \{\text{Red}, \text{Yellow}, \text{Green}\} \\ \mathcal{S}^{3} &\equiv& \{\text{Ripe}, \text{Not Ripe}\} \\ \mathcal{S}^{4} &\equiv& \{\text{Bruised}, \text{Not Bruised}\} \end{array} $$

then we can represent a ripe tomato at time t as:

$$ \begin{array}{@{}rcl@{}} \mathbf{x}_{t} &= \left[\begin{array}{ccc} \text{Tomato} \\ \text{Red} \\ \text{Ripe} \\ \text{Not Bruised} \end{array}\right] \end{array} $$

and a sample sliding window, X_t, for L = 3, can be obtained as follows:

$$ \begin{array}{@{}rcl@{}} \mathbf{X}_{t} &= \left[\begin{array}{ccc} \text{Tomato} & \text{Tomato} & \text{Tomato} \\ \text{Green} & \text{Red} & \text{Red} \\ \text{Not Ripe} & \text{Not Ripe} & \text{Ripe} \\ \text{Not Bruised} & \text{Not Bruised} & \text{Not Bruised} \end{array}\right] \end{array} $$

In post-hoc local explanation methods, we can construct an importance matrix Φ_t = {ϕ_jℓ,t} to provide feature importance scores for an instance X_t = {x_jℓ,t} at a given time step t. A local explanation method aims to find the importance of each covariate. We consider two local explanation methods, namely, omission and SHAP, and compare their performances against a random baseline.

3.3.1 Random baseline

In this approach, we randomly rank features from the most important to the least important.

3.3.2 Omission

In omission, the estimated importance of a regressor in question, x_jℓ,t, is denoted as ϕ_jℓ,t. This importance score is found by removing the regressor from the sliding window matrix, which we represent as $\mathbf {X}_{t \backslash x_{j \ell ,t}}$, and measuring the effect. That is,

$$ \phi_{j \ell,t} = f(\mathbf{X}_{t}) - f(\mathbf{X}_{t \backslash x_{j \ell,t}}) $$

(2)

Unlike a natural language processing problem where we can easily remove words by replacing it with zeros, we cannot just remove a feature with zeros without consequences in the regression setting. If the features values are replaced with zeros, then the interpretability method will learn that when a covariate x_jℓ,t is zero, it has no contribution to the prediction [43]. Alternative approaches can be replacing removed features with local mean, global mean, local noise and global noise. Note that local refers to a single sample and global refers to all the samples of that feature in the dataset. On the other hand, adding local and global noise can put extra peaks and slopes to the input, which are usually important for the prediction. Thus, we choose to test the omission method with local and global mean replacement. The local mean calculates the average value of a feature in a given window slice. This is done by performing a column-wise average over a window in X_t (3). The global mean is time invariant, and is the average feature value of a given time series of length T (4).

$$ \begin{array}{@{}rcl@{}} \text{Local Mean: } && \mu^{\text{loc}}_{j,t} = \frac{1}{L} \sum\limits_{\ell=1}^{L} x_{j \ell,t} \end{array} $$

(3)

$$ \begin{array}{@{}rcl@{}} \text{Global Mean: } && \mu_{j}^{\text{glo}} = \frac{1}{T} \sum\limits_{t=1}^{T} x^{[j]}_{t} \end{array} $$

(4)

3.3.3 SHAP

SHAP is a post-hoc and model agnostic approach which follows a very similar logic to many other popular interpretability methods such as LIME [40] and DeepLIFT [42]. All these methods learn a local linear model to explain a more complex model. As such, these methods are also referred to as additive feature attribution methods. SHAP is the only local explanation method that satisfies three desirable properties: local accuracy, missingness, and consistency [23].

In our analysis, we use two SHAP based approaches, DeepSHAP [23] and TreeExplainer [24], and two model-specific methods that approximate SHAP values for neural networks and tree-based models, respectively. We experiment with DeepSHAP method for TDNN and LSTM models, and TreeExplainer for the GBR models, and use the shap library in Python [23] in our implementations.

3.4 Evaluation metrics

We propose two new evaluation metrics for local explanation methods in time series forecasting models. Specifically, we can organize the top K features according to a local explanation metric. These are sorted according to largest ϕ_ij,t values. When we take out the top K features from X_t, which, without loss of generality, is defined as X_t,∖1:K. This is a combination of defined covariates, x_jℓ,t and random covariates, r_jℓ,t, sampled from the marginal distribution of the respective feature space $\mathcal {S}^{j}$. For example, a particular model may have a window of length L = 2 with three features at each time slice, J = 3. Then, a local explanation model determines the importance of variables ϕ_t, where ϕ_12,t > ϕ_31,t > ϕ_jℓ,t ∀(j,ℓ)∉{(1,2),(3,1)}. We represent the removal of the top two most important features (i.e., (j = 1,ℓ = 2) and (j = 3,ℓ = 1)) as

$$ \begin{array}{@{}rcl@{}} \mathbf{X}_{t,\backslash 1:2} &= \left[\begin{array}{cc} x_{11,t} & {r_{12,t}} \\ x_{21,t} & x_{22,t} \\ {r_{31,t}} & x_{32,t} \end{array}\right] \end{array} $$

Due to the stochastic nature of this process, in order to perform the feature ablation, we need to collect the expected value of the ablated feature. We represent this as $\mathbb {E}_{r}[\cdot ]$.

We next define two evaluation metrics to evaluate the local fidelity of local explanation methods. Local fidelity is an important measure for explanation methods. It evaluates the level of alignment between the interpretable model and the black-box model [14]. Local states that we look for this alignment is the neighborhood of an instance. Local fidelity can be measured by k-ablation methods [43], where we delete features in the order of their estimated importance for the prediction. Nguyen [34] uses two metrics to measure local fidelity: Area Over the Perturbation Curve (AOPC) and Switching Point (SP). However, similar to other existing evaluation methods, AOPC and SP are only used for classification tasks.

To measure local fidelity for a multivariate time series forecasting task, we define two new metrics: AOPCR and APT. These metrics can be considered as variants of AOPC and SP, and they are specifically designed for evaluating interpretable AI methods for time series forecasting task. AOPCR and APT measure the local fidelity in two different ways. AOPCR measures the effect of removing the top K features, and APT measures the percentage of features that need to be removed to pass a certain threshold. AOPCR focuses on a small percentage of the most important features whereas APT usually requires the removal of a higher percentage of features.

3.4.1 Area over the perturbation curve for regression (AOPCR)

The area over the perturbation curve for regression at time horizon τ, denoted as AOPCR_τ, is obtained as

$$ \text{AOPCR}_{\tau} = \frac{1}{K} \sum\limits_{k=1}^{K}\mathbf{F}_{\tau}(\mathbf{X}_{t}) - \mathbf{F}_{\tau}(\mathbf{X}_{t,\backslash 1:k}) $$

(5)

Then, the total area over the perturbation for regression is the average of all the time steps τ = 1,…,t₀, where

$$ \text{AOPCR} = \frac{1}{t_0}\sum\limits_{\tau=1}^{t_0}\text{AOPCR}_ \tau $$

(6)

In its current state, AOPCR introduce random variables due to the feature removal procedure. In order to explicitly calculate AOPCR and AOPCR_τ, we collect the expected value of the ablated features, and compute AOPCR_τ with this expected value, denoted by $\widehat {\text {AOPCR}}_{\tau }$. That is,

$$ \begin{array}{@{}rcl@{}} \widehat{\text{AOPCR}_{\tau}} &=& \mathbb{E}_r[\text{AOPCR}_{\tau}] \end{array} $$

(7)

$$ \begin{array}{@{}rcl@{}} &=& \frac{1}{K} \sum\limits_{k=1}^{K}F_{\tau}(\mathbf{X}_{t}) - \mathbb{E}_r\left[F_{\tau}(\mathbf{X}_{t,\backslash 1:k})\right] \end{array} $$

(8)

where the source of randomness, r, is the randomly drawn covariates, r_jℓ,t. Similarly, $\widehat {\text {AOPCR}} = \mathbb {E}_r[\text {AOPCR}]$.

3.4.2 Ablation percentage threshold (APT)

APT provides an alternative way to measure local fidelity. In classification, the switching point [34] is defined as the percentage of features that needs to be deleted before the prediction switches to another class. For regression, we can define the switching point as a point above and below the original prediction by a predefined threshold distance.

In this approach, we take all J features and sort them by importance. Then, we remove K features from the top or the bottom, stopping when the prediction changes by a pre-defined factor, α. The percentage of features that need to be removed until the prediction passes the threshold is reported as the APT score at the particular time step. A lower APT score means a lower percentage of features has to be deleted to pass the threshold, which shows a higher local fidelity.

We define APT at time horizon τ with significance factor α as follows.

$$ \begin{array}{@{}rcl@{}} \text{APT}_{\tau,\alpha}\ &=& \underset{k \in \{1,\hdots,J\}}{\arg\min}\frac{k}{J} \end{array} $$

(9)

$$ \begin{array}{@{}rcl@{}} \text{such that:} \ &&\mathbf{F}_{\tau}(\mathbf{X}_{t}) (1 + \alpha) > \mathbf{F}_{\tau}(\mathbf{X}_{t,\backslash 1:k}) \end{array} $$

(10)

Note that in order find the lower bound significance threshold, α needs to be set to a negative number. This represents when a predicted value has gotten significantly smaller due to feature removal. The total ablation percentage threshold is a simple average over the time index:

$$ \text{APT}_{\alpha} = \frac{1}{t_0}\sum\limits_{\tau=1}^{t_0}\text{APT}_{\tau,\alpha} $$

(11)

Finally, to convert the theoretical metric, APT_α, into an experimental metric, we take the expected value, $\widehat {\text {APT}}_{\alpha } = \mathbb {E}_r[\text {APT}_{\alpha }]$

3.5 Experimental setup

In our numerical experiments, we consider four diverse datasets with different characteristics in terms of size, and observed seasonality/trends among others. We use a sliding window method for framing the datasets, and employ a 60-20-20% train-validation-test split where the last 20% of the sliding windows are added to the test set. Input window size (i.e., look back window) and prediction window size for each dataset are provided in Table 1. We perform a detailed hyperparameter tuning for all three models using a grid search approach, where we consider the hyperparameter values given in Table 2. For hyparameter tuning, the models are trained on the training set and evaluated on the validation set. Afterwards, the train and validation datasets are combined and the dataset-model pairs with the best hyperparameters are retrained using the combined dataset and evaluated on the test set. The best performing hyperparameters for each dataset-model pair are shown in Table 3. For the TDNN and LSTM models, we experiment with different number of layers, hidden units and dropout rates. For the LSTM model, when multiple layers are stacked, each LSTM layer returns its hidden states instead of its output to the next layer. For the GBR models, we test three important hyperparameters which are the total number of tress in the ensemble (# of trees), the number of leaves in each tree (max depth) and the minimum number of samples required to split an internal node (min samples split).

Table 2 The hyperparameter tuning search space

Table 3 The hyperparameter values (LSTM/TDNN: {# of layers, # of units, dropout rate}, GBR: {# of trees, max depth, min samples split})

For the AOPCR and APT metrics, we estimate the expected values of the metrics by taking numereus Monte Carlo samples. The ablated features are randomly replaced with in-sample values, proportional to their distribution.

Any biasing choice in the design of the experiment can be a threat to the external validity. To evaluate the explanation methods, we arbitrarily choose a K value and a threshold value for AOPCR and APT methods, respectively. A very small value can make the AOPCR and APT methods too sensitive and make the resulting scores incomparable. Thus, we found a K value of 10 for AOPCR to be suitable for the analysis. Additionally, for APT, a very large value can make it impossible for an ablated sample to pass the threshold and again result in incomparable scores. For the threshold value in APT, we experimented with multiple values, and found that 10% is an ideal value for comparing different methods and models for all the datasets.

In order to reduce the randomness in the evaluation metrics, we added an early stopping condition. Once the margin of error for the $\widehat {\text {AOPCR}}$ (or $\widehat {\text {APT}}$) statistic was less than 0.05%, with 95% confidence (assuming a Gaussian distribution of the statistic), we ceased taking more samples. This was a natural stopping condition, which provided stable results.

A summary statistic can often contain a threat to the conclusion validity. In evaluations, we need to take the average of the scores over Monte Carlo samples and forecasting horizons, t₀. However, since the important features for the model can vary over τ ∈{1,…,t₀}, the scores can also vary across the same interval. Therefore, we compute the confidence intervals separately for each forecasting horizon. Once every forecasting horizon lies in a tolerable confidence interval, the scores are first averaged over Monte Carlo samples and then over t₀.

4 Results

We perform various numerical experiments to illustrate the role of proposed evaluation metrics for interpreting time series forecasting models. We first discuss the predictive performances of the considered time series forecasting models. Then, we compare different explanation methods for these models using our evaluation metrics. Next, we examine the predictive power of the identified features by only considering those for model training, which further provide evidence on the usefulness of the explanation methods and the evaluation metrics. Finally, we provide our observations on the sensitivity of the local fidelity metrics with respect to the model parameters.

4.1 Model performances

We compare the performance of the three models (LSTM, TDNN and GBR) over four datasets (Electricity, Rossmann, Walmart and Ohio). We use Normalized Root Mean Squared Error (NRMSE) and Normalized Deviation (ND) to assess the predictive performance, which can be obtained as

$$ \begin{array}{@{}rcl@{}} \text{NRMSE}(y, \hat{y}) &=& \frac{\sqrt{\frac{1}{N} \sum\limits_{i=1}^{N}(\hat{y}_{i} - y_{i})^{2}}}{y_{\max}-y_{\min}}, \\ \text{ND}(y, \hat{y}) &=& \frac{\sum\limits_{i=1}^{N}\vert\hat{y}_{i} - y_{i}\vert}{\sum\limits_{i=1}^{N} \vert y_{i} \vert} \end{array} $$

(12)

NRMSE, a popular error measure for evaluating time series models, can be particularly preferred when outliers are rare and not important to the user [41]. In NRMSE, we choose the spread as the difference between the maximum and the minimum value of the training dataset ($y_{\max \limits }-y_{\min \limits }$). However, this error measure may not be an accurate representation of the model performance when there are large scale differences between multiple time series in the datasets. Thus, we consider a second error measure, ND, which can account for the scale differences as the differences are divided by the true values. Table 4 provides the summary statistics on model performances, including mean NRMSE and ND values, along with the standard deviation (std) and 95% confidence intervals (CIs) around the calculated values.

Table 4 Comparison of TDNN, LSTM and GBR models on the Electricity, Rossmann, Walmart and Ohio datasets

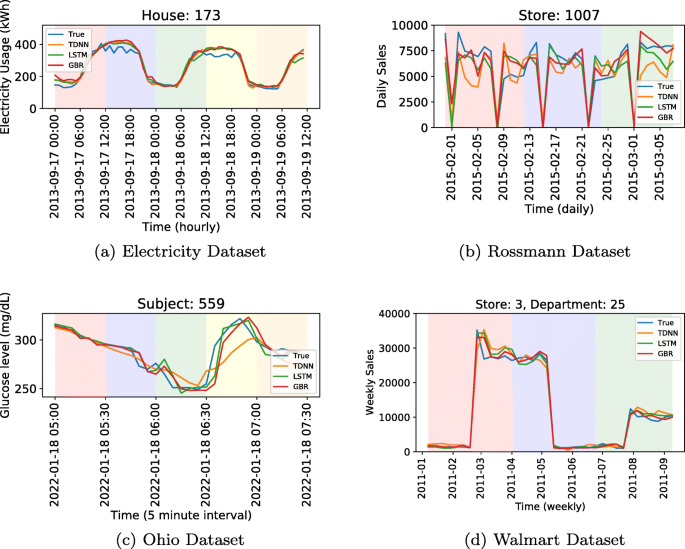
Overall, LSTM and GBR models perform significantly better than the TDNN models considering both NRMSE and ND values. GBR consistently performs the best, whereas LSTM is better than the TDNN models for all the datasets except the Electricity dataset. Note that the clear performance ranking of the three prediction models (e.g., TDNN ≺ LSTM ≺ GBR) is useful for understanding the link between the model performance and the interpretability. Furthermore, we observe that the error rates change considerably by the dataset, and the models perform the best for the Electricity and Ohio datasets, and worse for the Rossmann dataset. Interestingly, there is a significant difference between NRMSE and ND values for the Walmart dataset, which is possibly due to large fluctuations in values in the Walmart dataset.

We provide illustrations of the predictions for these three models on randomly sampled time series from each dataset in Fig. 3. Each background color on the figures corresponds to a separate prediction window. We note that all three models are able to generate conformal predictions, and capture the trends for the provided samples.

Fig. 3

Visualization of models’ predictions on random time series samples. Each background color corresponds to a separate prediction window. Each model generates predictions that can capture the trends for the provided sample

4.2 Evaluation of local explanations

We experiment with three AI interpretability/explanation methods (Omission (Global), Omission (Local), SHAP) and a random baseline to examine the three time series forecasting models. We repeat this analysis for all four datasets, and compare the performances of the explanation methods using AOPCR (see Table 5) and APT (see Table 6) metrics.

Table 5 AOPCR scores for the electricity and Rossmann datasets

Table 6 APT % scores for the Electricity and Rossmann datasets

First, we compare the explanation methods for each model. For the GBR model, SHAP performs significantly better in all four datasets considering both AOPCR and APT metrics. Thus, the results suggest that SHAP is easily able to identify the important features in the GBR model, and works well for explaining the tree-based models. For the TDNN model, the global omission and SHAP methods perform relatively similar and better than the local omission method. Considering the computational burden, we recognize that global omission might be preferrable over SHAP due to its simplicity without loss of accuracy. For the LSTM model, overall, we make similar observations to those of TDNN, where the global mean replacement and SHAP methods perform better than the local mean replacement, except for one case for the Walmart dataset, where APT values show that local mean replacement performs the best to explain the positive contributions.

Second, we compare the explanation methods independent of the machine learning models. As expected, random explanations (e.g., randomly selecting features to be removed) lead to the worst scores in almost all cases. In fact, the APT scores can be high for random explanations, even close to 100%. Note that, this is observed because, for a given sample, if all the features are removed and the prediction does not pass the threshold, the APT scores of 100% are assigned. However, in some cases (e.g., for the Walmart and Ohio datasets), the APT scores for local omission is higher than the random baseline. In APT scores of the Walmart dataset, we observe that the scores vary significantly for the local omission where it ranks first for positive case of the LSTM model but performs worse than the baseline in other cases. This result might indicate that local mean replacement is not a reliable baseline for omission methods. Mujkanovic [33] makes a similar observation, and suggests that global mean replacement is a better alternative to local mean replacement since it removes the most information while inserting the least accidental structure. Global omission method outperforms the local omission in almost all of the cases, which indicates that global omission is the preferred option as a local explanation method for time series forecasting. In general, SHAP is the best approach to interpret the model predictions, which is followed by the global omission method. This observation is intuitive since SHAP method is more complex and has the ability to account for the interactions between the features unlike the omission methods. However, the results also indicate that, it can perform equally or worse than simpler approaches in select examples, which shows that there might not be a uniformly superior explanation method for time series forecasting.

Lastly, we compare the evaluation metrics. AOPCR and APT give two different views on local fidelity. Our experiments show that these local fidelity scores do not have to correlate, therefore, each method should be used based on the intended experiment. For instance, if the objective is to correctly identify the importance of a predetermined number of top features, AOPCR should be used.

In contrast, if the objective is to examine the general explainability of the model, APT could be preferrable.

4.3 Impact of Feature Selection

For further validation of the explanation methods (e.g., Omission and SHAP) and the interpretability performance metrics (i.e., AOPCR and APT), we retrain the models only with the top 10 most significant features (which is an arbitrarily selected number of features) identified by the local explanation method. Note that the number of features considered in a time series forecasting task is dependent on standard features (e.g., Promo in Rossmann dataset) as well as sliding (input) window size (e.g., 30 in Rossmann dataset). All such features in the datasets have actual meanings (e.g., see Fig. 1). For example, “Promo-1” feature in the Rossmann dataset corresponds to whether there was an actual promotion on the day before the first prediction.

For this experiment, the best performing explanation method (SHAP) and time series forecasting model (GBR) are used. SHAP is then compared with three alternative feature selection methods, namely, Mutual Information, F Statistic and Tree (Gini) Importance. Table 7 shows the NRMSE and ND error on all four datasets for the GBR model when it is trained with all the features, and only with the 10 most significant features determined by the feature selection methods. The results show that SHAP performs consistently well as a feature selection method across different datasets. Moreover, we observe that using a fraction of the features leads to significant savings in terms of model training times.

Table 7 Performance of the GBR model trained with all available features and only with the top 10 most significant features determined by different feature importance assessment strategies

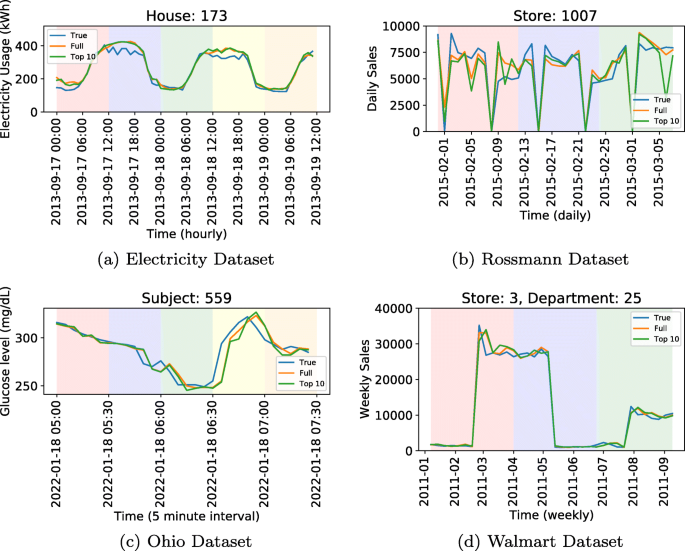
Sample predictions of the GBR model that uses top 10 features (determined by SHAP) and all the features are illustrated in Fig. 4, where the identical random samples in Fig. 3 are used for consistency. GBR produces a slightly worse accuracy when only a fraction of the features are used on all four datasets. These results help further validating the ability of the local explanation method to find the most significant features. In addition, we observe that local explanations can potentially be used as a feature selection method to find the most useful features in a given dataset.

Fig. 4

Visualization of predictions for the GBR model trained on all available features and only with the top 10 most significant features determined by the SHAP method

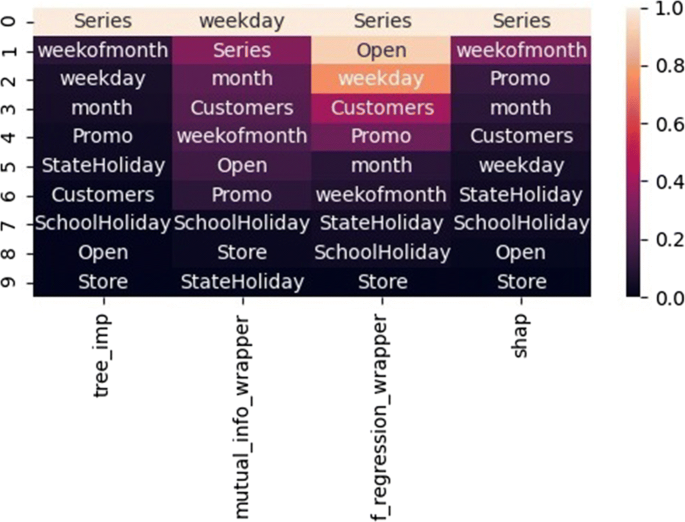
We also provide the normalized global feature importances as a heatmap for the Rossmann dataset in Fig. 5 as a representative example. We rank the features using four methods, namely, Mutual Information, F-Statistic, Tree Importance and SHAP. Mutual Information and F-Statistic are popular filter-based feature selection methods that measure the importance of features independent of the machine learning model used for prediction. Tree Importance method calculates the feature importance values as the decrease in node impurity weighted by the probability of reaching that node, where each node is associated with a feature, and probability value is obtained as the ratio of instances reaching the node divided by total number of instances. Finally, SHAP computes a local explanation for each sample in the dataset. These features are then averaged to obtain the global feature importances. Note that, we normalize these values to suppress the time index for the purpose of providing more intuitive results over standard features. Three of the methods find the time series feature (Series) to be the most important. All methods assign low importance to the Store feature and holiday related features. This is reasonable since these features themselves have very low predictive ability. Overall, we observe that there is a high level of agreement between Tree Importance (tree_imp) and SHAP, with the time series (Series) feature being the most important in both cases, which is followed up by the “weekofthemonth” feature. Other methods (i.e., Mutual Information and F-Statistic) provide somewhat conflicting feature importance values. However, inherent correlations between the features must also be taken into account when assessing the impact of feature selection on the model performance.

Fig. 5

Normalized global feature importances for the Rossmann dataset obtained by different feature selection strategies and SHAP method with the GBR model

4.4 Sensitivity analysis

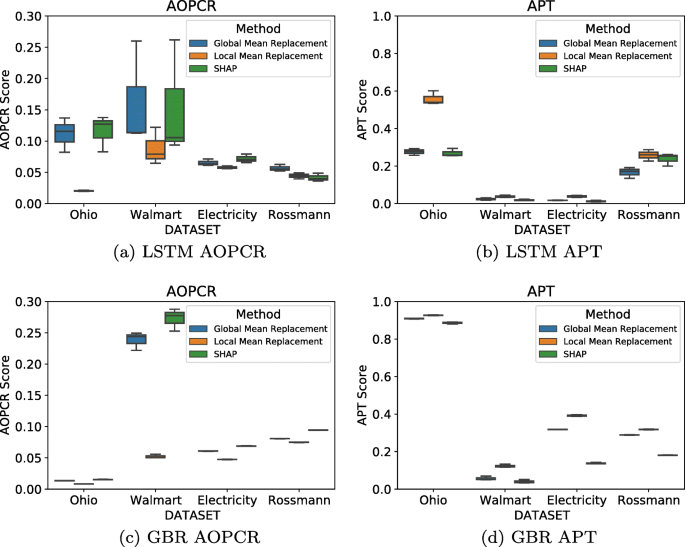
We next measure the sensitivity of the local fidelity (evaluation) metrics with respect to the time series forecasting model parameters. First, we retrieve the top three LSTM and GBR models for each dataset after the hyperparameter tuning. These models are selected based on the NRMSE metric. Then, SHAP explanations are generated for each model. After that, the AOPCR and APT scores are calculated using the local explanations in order to measure the sensitivity of the local fidelity metrics with respect to the model parameters.

Figure 6 shows that, for local interpretability methods such as SHAP, the effectiveness of the method changes based on the predictive model’s performance. If the predictive model has low accuracy, then the explanations generated on top of these models also tend to have high errors. As such, the change in the model hyperparameters may result in different degrees of change on the local fidelity metrics. The results also indicate that the local explanations generated for the LSTM models are more sensitive to the model hyperparameters. On the other hand, for the GBR models, we see a clear and robust ranking of local explanations with both local fidelity metrics across all datasets.

Fig. 6

Sensitivity of the explanation methods and evaluation metrics with respect to the forecasting model parameters

5 Conclusion and future work

There has been a significant interest in AI interpretability mainly caused by the growing adoption of the machine learning systems. Even though there are some studies focusing on the interpretability of machine learning models for time series, most of the existing literature is focused on the time series classification task. There is relatively low research interest in interpreting time series forecasting models. An improved understanding on evaluating local explanations can contribute to a further progress in this area. Thus, we focus on evaluating local explanation methods for the multivariate time series forecasting problem.

Local explanations are typically computed by finding the importance of features towards the prediction. In this study, two new evaluation metrics are proposed for thorough comparison of the local explanation methods. Three local explanation methods are compared for the multivariate time series forecasting problem. More specifically, we first train three models (TDNN, LSTM, GBR) on four datasets (Electricity, Rossmann, Walmart and Ohio). Then, we evaluate the three local explanation methods for all the models using two new local fidelity metrics suitable for the time series forecasting tasks. Overall, we find that the SHAP method has the highest fidelity, especially for the tree-based models, and global mean replacement is a preferable choice over local mean replacement. The results are mostly consistent accross all the datasets, and we observe some discrepancies for the Walmart dataset, which might be attributed to the fact that this dataset is not as clean, more noisy, and contain more missing data points compared to the others. Additionally, we investigate the performance of SHAP as a feature selection method and measure the sensitivity of the local explanation methods with respect to model hyperparameters.

An area that could be further explored is the idea of placing more weight on immediate time steps. That is, we can modify the evaluation metrics as follows:

$$ \begin{array}{@{}rcl@{}} \text{AOPCR} &=& \frac{1}{t_0}\sum\limits_{\tau=1}^{t_0}\gamma^{\tau-1}\text{AOPCR}_{\tau} \\ \text{APT}_{\alpha} &=& \frac{1}{t_0}\sum\limits_{\tau=1}^{t_0}\gamma^{\tau-1}\text{APT}_{\tau,\alpha} \end{array} $$

By setting γ = 1, these metrics can be reduced back to our initially proposed evaluation metrics. As $\gamma \rightarrow 0$, more weight is placed on the initial terms in the expansion. The choice of γ could be application specific. For example, if a short-term weather model is being evaluated, it might be more important to predict the next day’s forecast compared to forecasting five days into the future.