Location via proxy:   [ UP ]  
[Report a bug]   [Manage cookies]                
Skip to main content
SpringerLink
Log in

Leader–Follower Tracking in Nonlinear Multi-agent Systems via Different Velocity and Position Graph Topologies with External Disturbance

  • Research Paper
  • Published:
Iranian Journal of Science and Technology, Transactions of Electrical Engineering Aims and scope Submit manuscript

Abstract

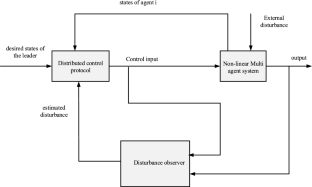
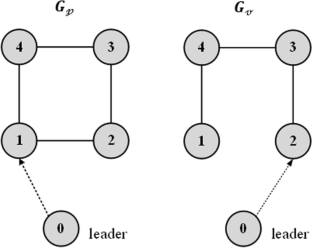
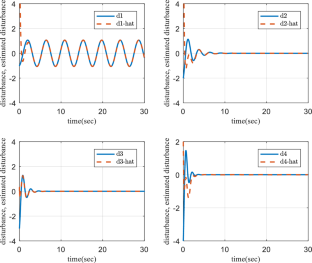
This paper proposes a novel distributed control algorithm for leader–follower tracking in nonlinear multi-agent systems via different velocity and position undirected graph topologies with external disturbance. Assuming that the disturbance is produced by linear exogenous systems, a disturbance observer without the position information based only on the velocity information of the agents is proposed. Next, graph theory, the Lyapunov approach and LaSalle’s principle are used to design a distributed control protocol for leader–follower tracking of MASs under different position and velocity undirected graphs with external disturbance. Finally, numerical simulations illustrate the efficacy of the proposed algorithms.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

Data Availability

The data used to support the findings of this study are available from the corresponding author upon request.

References

  • Cheng S, Jing L (2022) New conditions for consensus of second-order multi-agent systems. Iran J Sci Technol Trans Electr Eng 46(2):603–608

    Google Scholar 

  • Cong Y, Du H, Liu B, Zhang P, Li X (2023) Distributed constrained finite-time consensus algorithm for second-order multi-agent systems. Inf Sci 626(1):773–786

    Google Scholar 

  • Ding C, Li J, Jinsha L (2017) Distributed optimal consensus for multi-agent systems under independent position and velocity topology. J Dyn Syst Meas Control 139(10):1–8

    Google Scholar 

  • Du H, Wen G, Wu D, Cheng Y, Lu J (2020) Distributed fixed-time consensus for nonlinear heterogeneous multi-agent systems. Automatica 113(113):1–13

    MathSciNet  MATH  Google Scholar 

  • Eddy Y, Gooi H, Chen S (2015) Multi-agent system for distributed management of microgrids. IEEE Trans Power Syst 30(1):24–34

    Google Scholar 

  • Goldin D, Raisch J (2014) Consensus for agents with double integrator dynamics in heterogeneous networks. Asian J Control 16(1):30–39

    MathSciNet  MATH  Google Scholar 

  • Hamidi H (2018) An approach to intelligent traffic management system using a multi-agent system. Int J Intell Transp Syst Res 16(4):112–124

    MathSciNet  Google Scholar 

  • Hardy Y, Steeb W (2019) Matrix calculus, Kronecker product and tensor product: a practical approach to linear algebra, multilinear algebra and tensor calculus with software implementations, 3rd edn. World Scientific Publishing Company, Singapore

    MATH  Google Scholar 

  • He S, Liu X, Lu P, Liu H, Du C (2022) Leader-follower finite-time consensus of multiagent systems with nonlinear dynamics by intermittent protocol. J Frankl Inst 359(6):2646–2662

    MathSciNet  MATH  Google Scholar 

  • Hong Y, Hu J, Gao L (2006) Tracking control for multi-agent consensus with an active leader and variable topology. Automatica 42(7):1177–1182

    MathSciNet  MATH  Google Scholar 

  • Hu J, Feng G (2010) Distributed tracking control of leader-follower multi-agent systems under noisy measurement. Automatica 46(8):1382–1387

    MathSciNet  MATH  Google Scholar 

  • Jenabzadeh A, Safarinejadian B (2019) Distributed tracking of nonholonomic targets over multi-agent systems. IEEE Syst J 13(2):1678–1681

    MATH  Google Scholar 

  • Khodabandeh S, Kharrati H, Hashemzadeh F (2021) Control for leader-follower consensus of multi-agent systems with actuator faults using decentralized robust fault-tolerant control. Iran J Sci Technol Trans Electr Eng 45(2):529–541

    Google Scholar 

  • Liu C, Tian Y (2009) Formation control of multi-agent systems with heterogeneous communication delays. Int J Syst Sci 40(6):627–636

    MathSciNet  MATH  Google Scholar 

  • Liu C, Shi Y, Meng Y, Wang Y (2023) Leader-following consensus of multi-agent systems with connectivity-mixed attacks and actuator/sensor faults. J Frankl Inst 360(5):3592–3617

    MathSciNet  MATH  Google Scholar 

  • Liu L, Luo C, Shen F (2017) Multi-agent formation control with target tracking and navigation. In: Proceedings of the 2017 IEEE international conference on information and automation (ICIA), Macao, China, pp 98–103

  • Lu MA, Wu J, Zhan X, Han, Yan H (2022) Consensus of second-order heterogeneous multi-agent systems with and without input saturation. ISA Trans 126(1):14–20

    Google Scholar 

  • Luo X, Li X, Li S, Jiang Z, Guan X (2017) Flocking for multi-agent systems with optimally rigid topology based on information weighted Kalman consensus filter. Int J Control Autom Syst 15(1):138–148

    Google Scholar 

  • Luo Z, Sun Z, Peng J, Ma F (2021) Distributed control of multi-agent systems via static feedback controllers under directed networks. Trans Inst Meas Control 43(2):464–472

    Google Scholar 

  • Marina H, Jayawardhana B, Cao M (2016) Distributed rotational and translational maneuvering of rigid formations and their applications. IEEE Trans Robot 32(3):684–697

    Google Scholar 

  • Mei J, Ren W, Ma G (2011) Distributed coordinated tracking with a dynamic leader for multiple Euler-Lagrange systems. IEEE Trans Autom Control 56(6):1415–1421

    MathSciNet  MATH  Google Scholar 

  • Misir O, Gokrem L (2021) Flocking-based self-organized aggregation behavior method for swarm robotics. Iran J Sci Technol Trans Electr Eng 45(4):1427–1444

    Google Scholar 

  • Moradi M, Safarinejadian B, Shafiei M (2020) Distributed sliding mode leader-following consensus controller for uncertain time-delay linear parameter-varying multi-agent systems. J Vib Control 27(17):2136–2151

    Google Scholar 

  • Morbidi F, Mariottini G (2013) Active target tracking and cooperative localization for teams of aerial vehicles. IEEE Trans Control Syst Technol 21(5):1694–1707

    Google Scholar 

  • Nazarzehi V, Savkin A (2019) Decentralized three-dimensional formation building algorithms for a team of nonholonomic mobile agents. Int J Control Autom Syst 17(1):1–10

    Google Scholar 

  • Olfati-Saber R (2006) Flocking for multi-agent dynamic systems: algorithms and theory. IEEE Trans Autom Control 51(3):401–420

    MathSciNet  MATH  Google Scholar 

  • Olfati-Saber R, Murray R (2004) Consensus problems in networks of agents with switching topology and time delays. IEEE Trans Autom Control 49(9):1520–1533

    MathSciNet  MATH  Google Scholar 

  • Omidi E, Mahmoodi N (2016) Active vibration control of structures using a leader–follower-based consensus design. J Vib Control 24(1):60–72

    MathSciNet  MATH  Google Scholar 

  • Qiaoping Li Yu, Chen KL (2023) Predefined-time formation control of the quadrotor-UAV cluster’ position system. Appl Math Model 116(1):45–64

    MathSciNet  MATH  Google Scholar 

  • Qin J, Yu C (2013) Coordination of multi-agent interacting under independent position and velocity topologies. IEEE Trans Neural Netw Learn Syst 24(10):1588–1597

    Google Scholar 

  • Qin J, Ma Q, Shi Y, Wang L (2017) Recent advances in consensus of multi-agent systems: a brief survey. IEEE Trans Ind Electron 64(6):4972–4983

    Google Scholar 

  • Rahimi N, Binazadeh T (2018) Distributed robust consensus control for nonlinear leader–follower multi-agent systems based on adaptive observer-based sliding mode. J Vib Control 25(1):109–121

    MathSciNet  Google Scholar 

  • Rezaee H, Abdollahi F (2014) A decentralized cooperative control scheme with obstacle avoidance for a team of mobile robots. IEEE Trans Ind Electron 61(1):347–354

    Google Scholar 

  • Sun F, Wang R, Zhu W, Li Y (2019) Flocking in nonlinear multi-agent systems with time-varying delay via event-triggered control. Appl Math Comput 350(6):66–77

    MathSciNet  MATH  Google Scholar 

  • Tahoun A, Arafa M (2022) Adaptive leader–follower control for nonlinear uncertain multi-agent systems with an uncertain leader and unknown tracking paths. ISA Trans 131(3):61–72

    Google Scholar 

  • Tanner H, Jadbabaie A, Pappas G (2007) Flocking in fixed and switching networks. IEEE Trans Autom Control 52(5):863–868

    MathSciNet  MATH  Google Scholar 

  • Tian B, Zuo Z, Wang H (2016) Leader-follower fixed-time consensus of multi-agent systems with high-order integrator dynamics. Int J Control 90(7):1420–1427

    MathSciNet  MATH  Google Scholar 

  • Wang M, Zhang T (2021) Leader-following formation control of second-order nonlinear systems with time-varying communication delay. Int J Control Autom Syst 19(5):1729–1739

    MathSciNet  Google Scholar 

  • Wang Y, Liu Y, Li X, Liang Y (2023) Distributed consensus tracking control based on state and disturbance observations for mixed-order multi-agent mechanical systems. J Frankl Inst 360(2):943–963

    MathSciNet  MATH  Google Scholar 

  • Wang J, Zhang L, Li J (2016) Iterative learning consensus control for multi-agent systems under independent position and velocity topologies. In: 2016 Chinese control and decision conference (CCDC), Yinchuan, China, pp 6609–6614

  • Wen G, Duan Z, Chen G et al (2014) Consensus tracking of multi-agent systems with Lipschitz-type node dynamics and switching topologies. IEEE Trans Circuits Syst I Regul Pap 61(2):499–511

    MathSciNet  MATH  Google Scholar 

  • Yan C, Fang H (2019) Observer-based distributed leader-follower tracking control: a new perspective and results. Int J Control 94(1):39–48

    MathSciNet  MATH  Google Scholar 

  • Yan Z, Yue L, Zhou J, Pan X, Zhang C (2023) Formation coordination control of leaderless multi-AUV system with double independent communication topology and nonconvex control input constraints. J Mar Sci Eng 11(1):1–22

    Google Scholar 

  • Yao D, Li H, Lu R, Shi Y (2020) Distributed sliding-mode tracking control of second-order nonlinear multi-agent systems: an event-triggered approach. IEEE Trans Cybern 50(9):3892–3902

    Google Scholar 

  • Zamanian M, Abollahi F, Nikravesh SK (2020) Finite-time consensus of heterogeneous unknown nonlinear multi-agent systems with external disturbances via event-triggered control. J Vib Control 27(15):1806–1823

    MathSciNet  Google Scholar 

  • Zhang X, Xianping L (2013) Further results on consensus of second-order multi-agent systems with exogenous disturbance. IEEE Trans Circuits Syst 60(12):3215–3226

    MathSciNet  MATH  Google Scholar 

  • Zhao J, Liu G (2018) Time-variant consensus tracking control for networked planar multi-agent systems with non-holonomic constraints. J Syst Sci Complex 31(2):396–418

    MathSciNet  MATH  Google Scholar 

  • Zhao Y, Duan Z, Wen G, Zhang Y (2013) Distributed finite-time tracking control for multi-agent systems: an observer-based approach. Syst Control Lett 62(1):22–28

    MathSciNet  MATH  Google Scholar 

  • Zhao X, Liu W, Yang C (2019) Coordination control for a class of multi-agent systems under asynchronous switching. J Syst Sci Complex 32(4):1019–1038

    MathSciNet  MATH  Google Scholar 

  • Zheng Y, Ma J, Wang L (2017) Consensus of Hybrid multi-agent systems. IEEE Trans Neural Netw Learn Syst 29(4):1359–1365

    Google Scholar 

Download references

Funding

The authors received no financial support for the research, authorship, and/or publication of this article.

Author information

Authors and Affiliations

  1. Department of Electrical Engineering, Shiraz University of Technology, Modarres Blvd, Shiraz, 715555-313, Iran

    Seyyed Vahid Ghasemzadeh & Behrouz Safarinejadian

Authors
  1. Seyyed Vahid Ghasemzadeh
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Behrouz Safarinejadian
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Behrouz Safarinejadian.

Ethics declarations

Conflict of interest

The authors declared no potential conflicts of interest concerning the research, authorship, and/or publication of this article.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ghasemzadeh, S.V., Safarinejadian, B. Leader–Follower Tracking in Nonlinear Multi-agent Systems via Different Velocity and Position Graph Topologies with External Disturbance. Iran J Sci Technol Trans Electr Eng 47, 1525–1536 (2023). https://doi.org/10.1007/s40998-023-00632-7

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s40998-023-00632-7

Keywords

Search

Navigation