Deep learning-based approach for forecasting intermittent online sales

Abstract

Deep Neural Networks (DNN’s) present some of the leading applications of Artificial Intelligence (AI) which have proven suitability on various machine-learning use cases. Forecasting demand of intermittent on-line sales is a task which needs to be carried out automatically for a large number of Stock Keeping Units (SKU’s). This paper discusses the intermittent online sales and proposes an AI-based model for forecasting demand. We provide empirical evidence by utilizing data from 17 different sellers with approximately 3000 orders in total. Our findings indicate that thanks to their multi-layered learning structure, the DNN’s can provide up to 35% better accuracy than the classic models such as Moving Average, Exponential Smoothing, Croston’s method and ARIMA. Also, it was revealed that the time between orders’ arrivals follow Exponential distribution and the order sizes also generally follow Exponential distribution. Thus, most of the time, Poisson Exponential distribution can be used for modelling intermittent sales process through online platforms. The analyses show that Poisson Exponential distribution can generate values close to real sales with less than 7% error margin with real data.

1 Introduction

The development of online marketplaces has encouraged many sellers to sell their goods online. This development is reflected in the number of sellers and amount of sales that have skyrocketed during the recent years. According to the European Union statistics (2016) [44], the proportion of internet users who have ordered goods through the internet has risen from 50 to 66% during the years 2007–2016. The importance of accuracy in forecasting such sales has been increasing respectively. Increased forecasting accuracy helps especially the commercial sellers to decrease the bullwhip effect in their supply chain. This became especially important after the COVID-19 pandemic hit and e-commerce platforms saw a two to threefold increase in the orders. According to Alfonso et al. [2], revenues increased in the first half of 2020 for Amazon (34% year on year), Alibaba (27%), JD (28%), Shopify (74%), Rakuten (16%) and Mercado Libre (50%). As a side note, the terms “e-business” and “e-commerce” have been used to express different meanings in different contexts, but in general it is accepted that e-business has more general meaning and it covers e-commerce transactions.

Fast-growing e-business combined with the developments in the Artificial Intelligence and Machine Learning models motivates us to find more advanced approaches to model and forecast online sales. With this pace of growth of the e-commerce and the number of Stock Keeping Units (SKU’s), automated real-time working algorithms will have to be deployed in the future to handle the forecasting/inventory related tasks. Deep Neural Networks (DNN’s) constitute the backbone of many modern technologies (e.g., face recognition, computer vision, self-driving cars, Natural Language Processing, etc.). One main motivation behind this paper is to investigate the applicability of Deep Neural Networks (DNN’s) to forecasting the intermittent online sales. As of 2022 Q4, the share of the third-party sellers constitutes 59% of the total sales on Amazon. On special days (Black Friday, Cyber Monday), the sales of third-party sellers exceed one billion US dollars on Amazon, so, third-party sellers should not be underestimated [45]. Sales for many individual third-party sellers on online markets such as eBay, Amazon and Alibaba are intermittent and “nervous”, especially for small and medium size stores. There are multiple complications with predicting such data: skewed distributions, high variability, different demand drivers, to name a few. On some days, sellers receive several orders and then receive no orders during several consecutive days. There are no papers currently attempting to model the described situation in this specific context. Our paper is inspired by a real-life situation that the authors have faced after starting selling goods online. The authors had tried to forecast their sales for the following year and noticed that they do not follow regular distributions. This led to further analyses of the data. It was found out that DNN’s perform well for forecasting and Compound Distributions fit well for modeling purposes. As it will be discussed in the literature review section, DNN’s’ superiority have been proved in not only forecasting intermitted demand, but also in a wide variety of prediction tasks.

The origins of online selling date back to the mid-90 s; when eBay and Amazon were launched as pioneers in this field. Since that, electronic businesses have been the research topic of a significant number of articles. E-businesses have been analyzed from the aspect of Supply Chain integration by Lee and Whang [26]. They focus on information integration, synchronized planning, coordinated workflow and new business models and discuss how the integration of Supply Chains have been affected because of massive migration to online business. The article was written in the early 2000s, when the use of the internet started proliferating across the world. They had correctly predicted that the companies that successfully integrate their supply chains into e-business will gain significant competitive advantage [13]. This process is still ongoing, not all supply chains are connected from end to end and there is a long way to go in this field.

Swaminathan and Tayur [42] presented models used in supply chain and discussed ways to adapt the current models to e-business. They focus on visibility in supply chains, supplier relationships, distribution and pricing, real-time decision technologies and customization. The authors discuss the growing need for models that can give better insight into the effect of changing different parameters in the supply chain. Our paper tries to address this need and provide e-Supply Chains with better forecasting models. In quantitative research, testing and estimation require information about the population distribution. The traditional approaches do not work when usual assumptions about the population cannot be made. Bootstrapping method uses information based on the resamples from the sample to estimate the population distribution. It treats the sample as a population, draws X samples each containing n entries and computes the statistic that is of interest for the research. Then, the population statistics are estimated by considering all the bootstrap samples. A paper by Willemain, Smart and Schwarz [49] proposes using bootstrapping to forecast the demand for spare parts. They show that the proposed bootstrap method dominates the traditional Exponential Smoothing and Croston’s method. But the performance of the bootstrap method deteriorates with the increasing lead time. Other methods have been used in the literature are Single Exponential Smoothing [3, 10], Croston’s Method [6], Synthetos-Boylan approximation [43], Moving Average [36], Weighted Moving Average [38], Additive Winter [4], Grey Prediction Model [5], ARIMA [47] and Neural Networks (NN’s) [5]. Gutierrez et al. [14] describe lumpy demand forecasting using NN’s and compare their results with single exponential smoothing, Croston’s method, and the Syntetos–Boylan approximation. NN’s dominate the other traditional methods. The paper by Jiang et al. [18] discusses the application of Support Vector Machines (SVM) to modeling the spare part demand in the heavy-duty vehicle industry. In their case, the SVM approach results in better run times and better accuracy when compared to the Neural Networks (NN’s). Turkmen et al. [48] have investigated the application of Deep Renewal Processes to the intermittent demand forecasting. In their case, the LSTM-based recurrent neural networks outperform the traditional methods.

First research task of this paper is (1) to study the applicability of Deep Learning (DL) models to forecasting the sales of online stores. Making reliable forecasts for the upcoming periods by treating the data as time series is included in this article. We employ DNN’s to find the most suitable Neural Network (NN) architecture that would yield the least deviations from the actual values. DNN’s have been successfully applied to forecasting problems from different domains. The structure of the data that we use is similar to the applications in spare parts demand forecasting. (2) The second research task is to find statistical distributions to model the total sales for online stores. Intermittent online sales do not follow regular distributions and we attempt to find statistically appropriate distributions for such data.

The remainder of the paper is structured as follows: literature review provides an overview of the most recent articles on the topic, then methodology is explained. Result explains the findings of the research and provides the statistical tests. Finally, conclusions are presented with discussion.

2 Literature review: demand forecasting for intermittent demand

This section reviews some prior works on forecasting intermittent demand and how neural networks and related techniques have been applied to solve similar kinds of problems.

For intermittent demand, a great share of literature until the early 2010’s focuses on Croston’s Method; after that many hybrid methods in forecasting the intermittent Supply Chain demand patterns have been proposed such as the methodology described by Fu et al. [9]. Initial version of the Croston’s Method was found to have an error leading to the positive bias. Solis et al. [41] studied whether the two proposed corrections to the Croston’s Method (SBA and SBJ) are superior to each other or not. The results showed no significant difference between the two approaches.

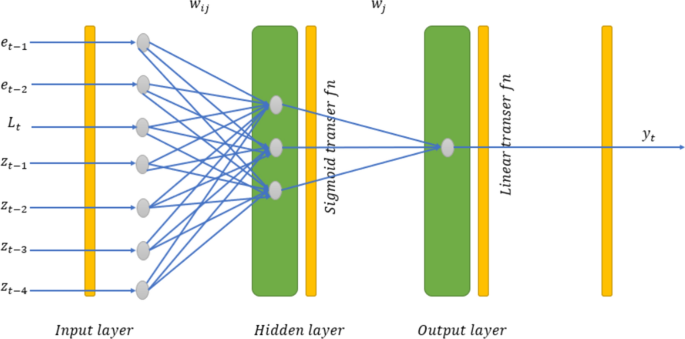
A hybrid model for forecasting was proposed by Khashei and Bijari [20]. According to this study, any forecasting problem can be divided into linear and non-linear components. Since ARIMA models assume that the generating process is stationary, and it does not depend on additional variables, they are used to model the linear portion. Then selected n last residuals (e_t’s), forecasted values (L_t) and z_t values from the ARIMA model are used as inputs to the multilayer perceptron where

$$\left({z}_{t}={\left(1-B\right)}^{d}\left({y}_{t}- \mu \right)\right)$$

(1)

and B is the backward shift operator, d is the order of differencing, y_t is the actual value of the observation at period t, and $\mu$ is the mean value. They use the sigmoid activation function in the NN’s and structure of the best fitted network is as in Fig. 1.

Fig. 1

The structure of NN used by Khashei and Bijari [20]

The number of residuals and z values were decided as results of repeated trials, as such there is no single way to determine the number and constitution of the inputs. The proposed model is claimed to dominate other hybrid approaches in MAE (Mean Absolute Error) and MSE (Mean Square Error) values.

Another academic work worth discussion is about application of NN’s to intermittent demand patterns by Kourentzes [22]. He discusses different ways to forecast the intermittent demand, especially comparing the variation of Croston’s method to NN’s. His findings indicate that NN’s do not provide better forecast accuracy than other classical approaches, however, they dominate when taking the service levels into consideration. The article uses 1000 items for analysis and calculates the model parameters on the dataset of 3000 time series that were used by Syntetos and Boylan [43]. Inventory simulations were done on these items and the service level results have been openly in favor of Neural Network models. There are several articles in the literature discussing the applications of the Artificial Intelligence and Deep Learning models to the problems in the industry. Li et al. [28] make a review of the application of these models to intelligent manufacturing. Quantitative models for evaluating Supply Chains are discussed by Lima-Junior and Carpinetti [29].

The applications of the NN and DL models to the Operations Management (OM) and Supply Chain Management (SCM) problems has been studied throughout the last two decades. Such problems include production planning and scheduling, Material Requirements Planning (MRP) and inventory planning. Lot Sizing problem which is used to determine the optimal production quantity for each period is solved by using NN’s in the article by Radzi et al. [34]. Their model inputs are holding cost, reorder cost and the demand values. Feed-forward multi-layered network with backpropagation learning algorithm was used. NN’s input layer consists of 14 nodes; 12 for the demand values for the time periods t = 1,2,…,12, 1 for the holding cost, 1 for the reorder cost. These values are then passed into the hidden layer consisting of 13 nodes. The output layer consists of 12 nodes with binary values. If the result of any node is 1, it means that an order is to be placed in that period. The model in question has provided better and faster solutions when compared to the classical models.

The paper titled “Export Sales Forecasting using Artificial Intelligence” authored by Sohrabpour et al. [40], and published in Technological Forecasting and Social Change, dives into the domain of international trade and investigates the efficacy of AI methods in predicting export sales. Through empirical analysis, the study evaluates multiple AI techniques, such as Genetic Algorithm, against conventional time series forecasting methods, revealing that AI-based approaches outperform traditional models by achieving an average prediction accuracy improvement of around 15%. These results underscore the substantial potential of AI in revolutionizing export sales forecasting, offering businesses valuable insights into optimizing their strategies and resource allocation for enhanced competitiveness in the global market landscape.

In their 2020 paper titled “Data Analytics in Supply Chain Management: Review of Machine Learning Applications in Demand Forecasting,” Aamer et al. [1] review the current state of the literature in the realm of the demand forecasting. They have found out that 77% of the articles used various ML techniques (such as NNs and SVM) for demand forecasting. Their second finding was that the ML algorithms can provide better accuracy and less computational cost.

In their 2019 article “A Comprehensive Literature Review of the Demand Forecasting Methods of Emergency Resources from the Perspective of Artificial Intelligence,” Zhu et al. [51] conduct a comprehensive examination of demand forecasting techniques for emergency resources, with a focus on artificial intelligence (AI). The authors survey a range of AI-based methods used in this context, revealing the multifaceted landscape of forecasting approaches. Throughout the review, the authors emphasize the importance of AI-driven strategies in accurately predicting the demand for emergency resources, shedding light on innovative methodologies that contribute to more effective disaster preparedness and response efforts.

One of the classical problems in the OM is demand forecasting. An interesting approach has been proposed by Qiu et al. [33]. It is an ensemble method, i.e., a combination of different models working together. The authors justify their choice as ensemble methods being statistically, computationally and representationally effective. Their method works as follows: a number of Deep Belief Networks (DBN’s) are trained with different numbers of epoch values. The outputs of DBN’s are fed into the Support Vector Regression (SVR) model. The outputs of the SVR become the predictions for the coming periods. The proposed model outperforms the different ML algorithms when applied individually. The application of the DL to the Newsvendor problem has been studied by Oroojlooyjadid et al. [31]. Forecasting and inventory optimization have been incorporated into a single model rather than dealing with them separately. One advantage of such models is that they do not need assumptions about the demand distributions. The authors also mention data features included in the model, although they do not explain in detail what these features are. Their main finding is that when the demand is volatile, DL models work well. This coincided with our findings. Their other contribution is the extension of the DL models to the (r, Q) inventory policies. Another interesting paper by Jeble et al. [17] investigates the impact of big data and predictive analytics capability on supply chain sustainability. The fact that predictive analytics (including forecasting) can help firms to become more sustainable is another driving factor of this paper.

Another DL-based approach for time series forecasting was proposed by Torres et al. [46] with application to electricity load forecasting. They use the H₂O library in conjunction with Apache Spark to speed up the calculation process. Since H₂O does not allow multi-step ahead forecasting, the authors divide the problem into h subproblems (h denoting the number of time periods to be forecasted) and solve them separately. They turn this drawback into advantage by allowing a different number of neurons for each subproblem that would result in minimized errors. Their model can predict the real consumption values with less than 2% error margin. Larrain [24] takes the discussion to the macro-financial level by comparing NN’s and Regression forecasts for the Purchasing Managers Index (PMI), T-Bill and Inventories. Their findings indicate that T-Bills can be used to forecast the PMI, PMI can be used to forecast the inventories. The forecasting of inventories is of paramount importance in Supply Chain Management.

Figueiredo [8] studied finding accurate forecasting models by employing the NN’s for new products that are to be sold via online platforms. The main challenge in e-commerce is that any new product is offered to millions of potential customers at a point in time which makes forecasting and inventory control difficult. It is difficult to predict how the market will react to the new product, thus, the potential sales amount becomes a question. He uses the following input variables to the NN model: duration of the selling season, type of the season, product class, profile, demand in the first two weeks and demand in the weeks 3–4–5–6 and total demand. For some cases, he adds two more variables to the list: cumulative demands and demand moving averages. Figueiredo’s model achieved 2.4–7.8% reduction in the average absolute error for 1000 lines in the test sample. This cannot be considered an important increase in the forecast accuracy. The author then proposes using combined forecast methods and this reduces the forecast error by 13.3% which can be considered as a significant change.

Ferreira, Lee and Simchi-Levi [7] discuss demand forecasting and price optimization for an online retailer called Rue La La. They achieve 9.7% increase in the revenues of the case company by applying more accurate forecasting methods and price optimization techniques. For the forecasting part, their findings show that regression trees with bagging outperform other regression methods in predicting the demand. For the pricing part, they propose a new formulation of the optimization problem and create an algorithm for the solution of this complex problem. Another importance of this paper is that they combine machine learning and optimization techniques into a pricing decision support tool that results in increase in the revenue of the online retailer.

The possibilities of using of artificial intelligence in supply chain management has been discussed recently [32]. Various technologies to support processes has been suggested in case studies [15] and literature reviews have been conducted to propose the application area [37]. However, the use of artificial intelligence technologies such as deep learning is far from maturity.

During the last decades, many versions of NN’s have been developed to address different questions in the industry and Artificial Intelligence. Recurrent Neural Networks (RNN’s) and its variants such as LSTM, Convolutional Neural Networks (CNN’s), Generative Adversarial Networks (GAN’s) and Kohonen Networks are a few examples. Most common applications of RNN’s have been in the field of speech recognition. Graves et al. [12] discuss speech recognition with deep bidirectional RNN’s. Their model works in both directions; conducts front and back propagation which outperformed the other approaches based on the TIMIT database at the time of publishing. CNN’s have been successfully applied to the image classification and face recognition types of tasks such as the model described by Krizhevsky et al. [23] and Lawrence et al. [25]. Another important paradigm developed in the field of machine learning is reinforcement learning. Different from supervised and unsupervised learning, reinforcement learning deals with the actions that need to be taken by an agent to maximize the reward. The rules are usually stochastic and in this sense reinforcement learning is a Markov Decision Process, sometimes they are referred to as approximate dynamic programming models. Reinforcement learning concept is successfully applied to robotics as discussed in the survey by Kober et al. [21]. They are especially useful in complex cases where classical Dynamic Programming falls short [11].

Besides searching for the articles related to the e-business demand analysis, we also conducted a search to find papers discussing methodologies to model intermittent sales. We found out that similar types of demand patterns are observed in service logistics. There are many papers in the literature dealing with modeling spare parts sales. Spare parts show similarities to online sales; their demands are generally intermittent and lumpy. Lengu et al. [27] propose compound distributions to model the spare part demands. Depending on the coefficient of variation and mode of the data, they recommend using Poisson-Logarithmic, Poisson-Pascal, Poisson-Geometric and Poisson-Poisson distributions. Snyder, Ord and Beaumont [39] propose a new model for slow-moving inventories. They compare the performances of Poisson, Negative Binomial and hurdle shifted Poisson distribution. Based on the analysis of 1046 car parts SKUs, they conclude that using dynamic schemes in favor of static ones can provide substantial benefits to the companies.

3 Methodology

This section provides an explanation of the data, mathematical models, distributions and overall approach used in the analyses of the data.

3.1 Data

The data collected covers a period of two years of online sales on eBay between April 2015 and January 2017. Banknotes, coins and other numismatics products were being sold; 121 orders were received. The data for early February were left out of consideration since it was the start up month of the sales and therefore, they do not realistically represent sales trends. We also acquired sales data of 16 different stores from eBay and its Turkish subsidiary GittiGidiyor. The data span a period of 2 to 4 years. The information related to the sales on online platforms are available on the feedback pages of the sellers as such, the findings of this research can be verified and reproduced easily. The distribution of data across categories is seen in Tables 1 and 2. The SKU’s can be held by the e-commerce platform owner, vendor, private seller depending on the configuration.

Table 1 The number of stores by categories

Table 2 Summary statistics of the data sets

Summary statistics of the Data Sets:

These data were deliberately selected from stores with intermittent demand; they do not represent the whole e-business, only the individual sellers with non-continuous demand are present in this data set. The stores are from very different fields as depicted in the Table 1 to demonstrate that the proposed methods in this paper work for many domains. We also randomly picked 50 different items to analyze and find out their demand patterns. These items included phone accessories, watches, home equipment, books, numismatics products, sports equipment, clothes and apparel. The data consists of the dates of orders for specific items and their respective amounts.

3.2 Classical forecasting models

In this paper we evaluate DNN’s and compare their performance with different classical demand forecasting methodologies. In the literature there are following approaches proposed by various authors and we applied them to our data to see the respective results:

• 1. Moving average (MA)

This method uses the average of n periods as a forecast for the next period. Simple moving average is the unweighted mean of the last n observations:

$${x}_{t+1}=\frac{{x}_{t}+ {x}_{t-1}+{x}_{t-2}...+{x}_{t-(n-1)}}{n}$$

(1)

• 2. Single exponential smoothing (SES)

Single Exponential Smoothing is used when data does not show any patterns of trend or seasonality. It is a method of smoothing the time series data by assigning exponentially decreasing weights to the older observations, thus, giving higher priority to the most recent observations. The formula used is

$${x}_{t+1}=\alpha *{x}_{t} + (1-\alpha )*{x}_{t-1}$$

(2)

where α is the smoothing factor between 0 and 1.

• 3. Double exponential smoothing (DES)

DES is used when the underlying data has a trend. It contains the smoothing factors α and β between 0 and 1 for data smoothing and trend smoothing, respectively. As in SES, the model assigns much higher weight to closer observations than to the older ones. ${x}_{1}, {x}_{2}, {x}_{3},..,{x}_{t}$ are the observations, ${s}_{t}$ is the smoothed value for period t and ${b}_{t}$ is the estimate of the trend for period t.

$${s}_{1}={x}_{1}$$

(3)

$${b}_{1}={x}_{1}-{x}_{0}$$

(4)

$${s}_{t}={\alpha *x}_{t}+(1-\alpha )*({s}_{t-1}+{b}_{t-1})$$

(5)

$${b}_{t}={\beta *(s}_{t}- {s}_{t-1})+(1-\beta )*{b}_{t-1}$$

(6)

To forecast m period ahead, the following formula is used:

$${F}_{t+m}={s}_{t} + {m * b}_{t}$$

(7)

• 4. Croston’s method

Croston’s method separates two processes: the time between order arrivals and the magnitude of the individual orders. Demand process is described with the equation x_t = y_t * z_t where y_t is a binary variable representing whether an order will arrive or not and z_t showing the magnitude of the order if it arrives. As Simple Exponential Smoothing results in higher noise, Croston’s Method is preferred when planning inventory levels.

• 5. Grey prediction models

The superiority of Grey prediction models is that they can be used with limited amounts of data to estimate the values of unknown parameters [19]. They are represented as G (n,m) where n is the order of the difference equation and m is the number of the variables. Grey models are used to reveal the realistic governing rules of the data [19]. GM (1,1) type of models are the most frequently used type of Grey models in the literature.

• 6. ARIMA (p, d, q)

Auto Regressive Integrated Moving Average (ARIMA) models are used extensively to forecast data that has the characteristics of non-stationarity. p shows the number of lags, d the degree of differencing and q the order of the moving average model. ARIMA is suitable for stationary data; thus, if data’s mean and/or variance changes over time, transformations need to be used. We used log transformation in this article. The general formula for ARIMA is:

$$\hat{y}_{t} = \mu + \phi_{1} y_{t - 1} + \ldots + \phi_{p} y_{t - p} - \theta_{1} e_{t - 1} - \ldots - \theta_{q} e_{t - q}$$

(8)

where; ŷ_t: forecast for period t. ϕ’s and θ’s: Coefficients of the model.

3.3 Neural networks and deep learning models

DNN is currently one of the most promising Artificial Intelligence technologies and we investigated their power in intermittent demand forecasting. In general, NN’s are composed of algorithms that imitate the learning process of human brains. They are powerful tools to recognize patterns in a wide variety of data; they can be used for classification, regression and similar tasks. NN’s take numerical data as inputs, map the relationship between inputs and outputs by assigning weights to the inputs. This weight assigning process is an iterative one and there are different methods to achieve close-to-optimum values. After a model is trained, it can be used for predicting future inputs. NN’s are defined as “data-hungry” i.e., they need a lot of data for training to achieve the desired level of accuracy. There are plenty of papers discussing the application of NN’s to the forecasting, classification and regression models.

NN’s contain an input layer, hidden layers and an output layer. There are different activation functions used such as Sigmoid and RELU depending on the situation. The model fine tunes the weights to find the function that minimizes a certain loss function. When there is more than one hidden layer, the model can be classified as a Deep Learning (DL) model. More hidden layers allow to reveal a more complex relationship between the inputs and outputs. Development of the DL models have increased the power of working with unlabeled/unstructured data.

There are several properties of the NN’s that make them attractive for forecasting tasks for researchers and practitioners. First important property is that they do not have any a priori assumptions regarding the distribution of the underlying data and the demand rate which becomes a problem when dealing with the traditional forecasting methods. Another important characteristic of NN is that they can generalize. As we will discuss in the Results section, DNN’s can perform well even on the unseen part of the data. Thirdly, they are universal approximators and can estimate the complex nonlinear relationship between the inputs and outputs [50].

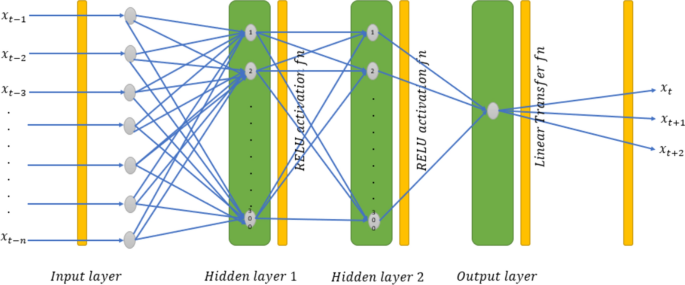
In addition to the traditional models, we tested two different types of NN’s; one for one-step ahead forecasts and one for three-step ahead forecasts. We used the Keras library in Python with TensorFlow backend to do the calculations. The architecture of the NN’s used for the LSTM model is depicted in Fig. 2.

Fig. 2

The architecture of the LSTM Network

LSTM model uses the last 12 months’ data as input, passes through two hidden layers each with Rectified Linear Unit (RELU) activation and 300 nodes. The outputs of the model are ${x}_{t},{x}_{t+1}, {x}_{t+2}$ which are the forecasts for the next 3 periods. The formula for RELU is

$$f\left( x\right) = x^{ + } = \max \left( {0,x} \right)$$

(9)

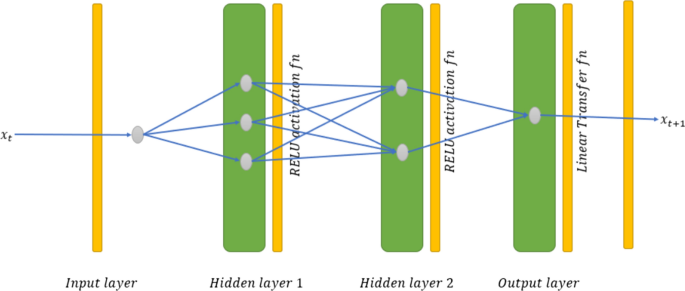
Ordinary Neural Network structure is shown in Fig. 3.

Fig. 3

The structure of the Ordinary Neural Network

Ordinary NN uses the last observation as input, passes it through 2 hidden layers with 3 and 2 nodes, respectively. The output is the forecast for the next period. As there is no single rule to decide on the parameters of the NN models, we also used trial-and-error method to find the most suitable parameter values.

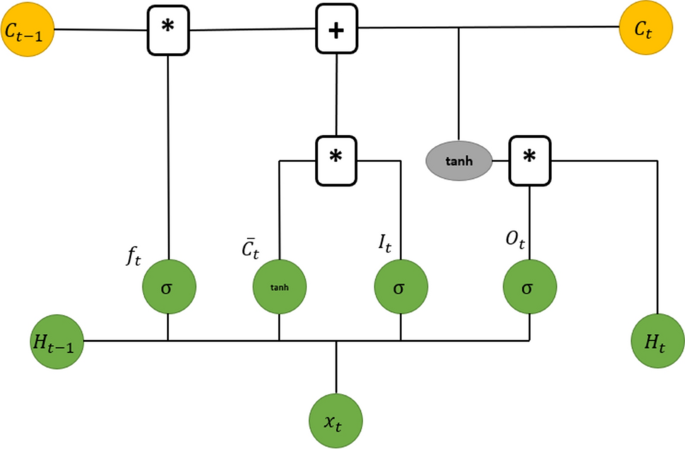
For multi-step ahead forecasting, we used Long Short-Term Memory (LSTM) models which were developed by Hochreiter and Schmidhuber in 1997 [16]. They are a special type of Recurrent Neural Networks (RNN’s) which can handle long-term dependencies. NN’s use backpropagation algorithm to update the weights of the network. Vanishing and Exploding gradients are well-known problems associated with this algorithm which cause difficulties in training the data. Also, traditional NN’s had the shortcoming that they were not able to link the past information to the current context and LSTM’s were created to address this problem. They have a channel to convey this information. Gates control how much of past data will be used in the cell state which is regulated by Sigmoid function. Sigmoid generates values between 0 and 1, which acts as a portion of each data to be utilized in the cell state. A diagram of the LSTM cell is depicted in Fig. 4.

Fig. 4

The structure of the LSTM Network

The notations used in the diagram are:

$${x}_{t}: Input Vector$$

$${H}_{t-1}: Output of the previous cell$$

$${C}_{t-1}: Memory of the previous cell$$

$${H}_{t}: Output of the current cell$$

$${C}_{t}: Memory of the current cell$$

The formulas 10–15 are associated with the LSTMs, where $\sigma$ stands for Sigmoid activation function and $tanh$ for Hyperbolic Tangent activation function:

$$f_{t} = \sigma \left( {x_{t} *U_{f} + H_{t - 1} * W_{f} } \right)$$

(10)

$${\overline{C} }_{t}=tanh ({x}_{t}*{U}_{c} + {H}_{t-1} * {W}_{c})$$

(11)

$${I}_{t}=\sigma ({x}_{t}*{U}_{i} + {H}_{t-1} * {W}_{i})$$

(12)

$${O}_{t}=\sigma ({x}_{t}*{U}_{o} + {H}_{t-1} * {W}_{o})$$

(13)

$${C}_{t}={f}_{t}*{C}_{t-1} + {I}_{t} * {\overline{C} }_{t}$$

(14)

$${H}_{t}={O}_{t}*{tanh(C}_{t})$$

(15)

W, U: weights.

It must be noted that LSTM’s have many variants and we used only one type for this study. To summarize, our selection criteria of LSTM over the other types of RNNs are the followings:

• handling long-term dependencies

• gating mechanisms

• avoiding gradient vanishing and exploding

• memory cells

• flexibility in sequence length

• efficient training

Nowadays, there are several tools on the market for applying Artificial Intelligence (AI) tools on the datasets. Some of them are open source and some are commercial. H₂O and Keras libraries in Python and R are examples of open-source libraries that are very powerful in real life applications. RapidMiner is an example of commercial tools that are widely utilized in the industry and in the academic world. With RapidMiner one can apply more than ten data mining methods (including DL) to any set of data in a few minutes. Main challenge in using the AI tools is the hyperparameter tuning. For a Long Short-Term Memory (LSTM) network, the learning rate, the number of training epochs, the size of training batches and the number of neurons are the major hyperparameters that need to be tuned for optimized results. Reimers and Gurevych [35] test 50.000 network configurations to find the patterns for optimal hyperparameters. Nejedly et al. [30] propose a method based on differential evolution genetic algorithm to produce the hyperparameters.

External factors like weather, month, country, and other relevant features can be added into neural networks to improve the accuracy of predictions for intermittent online sales. This is done as a part of the feature engineering and can significantly enhance the predictive power of the model. RNN’s, especially LSTM models are well-suited for capturing the temporal patterns. We did not do this since the articles we selected were random, however, if we focused on one industry, for example the fashion industry we would benefit from these additional features. Usually, the country names are one-hot encoded, weather-related factors (such as temperature, humidity, precipitation) are added as quantitative features.

3.4 Statistical distributions to model online sales

The methodology described in this part is similar to the one proposed by Thompson [45] and Lengu et al. [27]. Lengu et al. [27] used a similar approach to model the intermittent demand for the spare parts. The probability of having r orders in a two-week period is

$${p}_{r}= \frac{{\rho }^{r}*{e}^{-\rho }}{r!}$$

(16)

where $\rho$ is the mean rate of the orders.

The sum of r exponentially distributed independent orders with mean amount μ has the density function

$${g}_{r}= \frac{{x}^{r-1}*{e}^{-x/\mu }}{{\mu }^{r}*\left(r-1\right)!}$$

(17)

where x is the two-week order total. In other words, adding up Exponential random variables leads to Gamma distribution. That is what ${g}_{r}$ corresponds to: r independent orders, each having order sizes which are exponentially distributed.

Thus, the probability density function of the order totals is

$${\sum\nolimits_{r=1}^{\infty }{p}_{r}*g}_{r}= {e}^{\left(-\uprho -\frac{x}{\upmu }\right)}*\sum\nolimits_{r=1}^{\infty }\frac{{\mathrm{x}}^{r-1}*(\uprho /{\upmu )}^{r}}{r!*\left(r-1\right)!}$$

(18)

This probability distribution can be used to model intermittent online sales, for example in simulation or forecasting models.

3.4.1 Parameter estimation

To estimate the population mean rate ($\widehat{\rho }$) and the mean amount ($\widehat{\mu }$) of orders, we can collect samples from actual data and do the following computations. In terms of $\rho$ and μ, the mean ($\underset{\_}{}$ $)$ and variance (${}2$ $)$ of the total sales are

$$\overline{x}=\uprho *\upmu$$

(19)

$${s}^{2}=2*\uprho * {\upmu }^{2}$$

(20)

Therefore, the moment estimates for the parameters $\widehat{\rho }$ and $\widehat{\mu }$ are

$$\widehat{\upmu }=\frac{{s}^{2}}{2*\overline{x}}$$

(21)

$$\widehat{\uprho }=\frac{\overline{x}}{\widehat{\upmu }}= \frac{{2*\overline{x}}^{2}}{{s}^{2}}$$

(22)

If the given data contains the sale dates and amounts, then it is more reasonable to calculate $\rho$ and μ separately from the data; it is easier and more reliable.

There are two components of the problem discussed in this article: order arrivals and magnitude of the orders. The orders’ interarrival times follow exponential distribution, so, it is safe to assume that the order numbers follow the Poisson distribution. The magnitude of the orders follows Exponential distribution. To summarize, the sales data follows Exponential distribution and arrival of orders is a Poisson process.

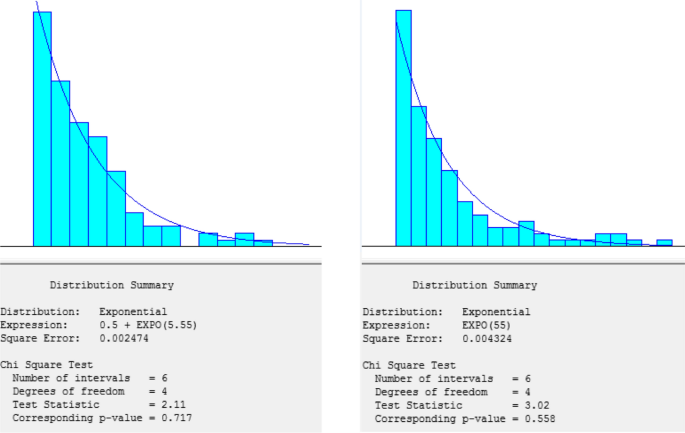
Figure 5 shows the histograms of the two processes for the main data. We fail to reject the hypothesis that interarrival times are exponentially distributed with p-value of 0.717, so, it can be assumed that order arrivals follow Poisson distribution. The second graph depicts the order sizes histogram, which has p-value of 0.558. In both cases, at 5% significance level we fail to reject the null hypotheses that data come from exponential distributions. This makes sense; because usually many people buy cheap items and a few people tend to buy expensive items. The number of buyers decreases exponentially from the cheapest to the most expensive items.

Fig. 5

Distribution summary for the main data (left: order arrivals, right: order sizes)

We propose to model such sales by using the Poisson Exponential compound distribution. In our case, the parameters of the distributions were calculated equal to 0.17 and 53.4 for μ and $\rho$, respectively. The model was used to test how it fits the data and the results have shown a good fit.

The goodness-of-fit was tested by using the Kolmogorov–Smirnov test. The proposed distributions were tested against the empirical distribution. The tests were built with the hypotheses given as follows:

• H₀: The data is distributed according to Poisson Exponential (PE) distribution

• H₁: The data is not distributed according to Poisson Exponential (PE) distribution

The empirical distribution of data is defined as

$${F}_{n}\left(x\right)= \frac{1}{n}*\sum_{i=1}^{n}{I}_{\left[-\infty ,x\right]}\left({X}_{i}\right)$$

(23)

where ${I}_{\left[-\infty ,x\right]}\left({X}_{i}\right)$ is the indicator function.

Based on the empirical distribution given above, Kolmogorov–Smirnov test statistic is calculated by using the following formula:

$${D}_{n}={sup}_{x}\left[\left|{F}_{n}\left(x\right)- {F}_{0}\left(x\right)\right|\right]$$

(24)

Then the D_n value is compared to the critical values taken from Kolmogorov–Smirnov tables. If D_n is less than the corresponding critical value, we fail to reject the null hypothesis that the provided data follows PE distribution. Otherwise, we reject the null hypothesis.

There are several assumptions behind the compound distributions. Firstly, the underlying distributions combined should be independent. Secondly, the compound distributions assume stationarity, i.e., properties of the combined distributions should stay constant over time. Thirdly, the combined distributions should be identically distributed. There are no “one size fits all” compound distributions for all the use cases, that is why, as discussed in the results section, we have tested a variety of them to find the most suitable ones.

4 Results and discussion

In this section, we discuss the findings of the paper. We applied the methodology discussed in Sect. 3 and recorded the results. Comparison was made between different approaches to find the level of effectiveness of applying DL to the problem in concern.

4.1 Forecasting online sales

We first discuss the results of NN’s applied to our problem. As illustrated in the Methodology section, we applied two different types of feed-forward network structures with back-propagation learning algorithms and compared the outcomes with the classical forecasting methods. Before applying these methods, we need to normalize the data by transforming them to the scale of [0, 1]. The formula used for normalization in the pre-processing stage is:

$${X}_{t}= \frac{{X}_{n} -{ X}_{min}}{{X}_{max} - {X}_{min}}$$

(25)

where X_t is the normalized data, X_n is the observed data point, X_min is the minimum value of the dataset and X_max is the largest value of the dataset.

Based on the sales data collected from 16 different online stores with 3000 orders in total, we conducted a thorough hyperparameter optimization experiment on the cloud service of AWS called Amazon SageMaker. The objective was set to validation root mean square error and Bayesian approach was selected for reducing the total run time. We provided ranges for the number of hidden layers, hidden nodes, the number of epochs, batch sizes and the activation functions. Maximum total number of training jobs was set to 50 and the maximum number of parallel runs was set to 5. The experiment took 30 min to run. Based on the optimal hyperparameters, we created a script on Python Jupyter Notebook with Keras library installed.

Overfitting is a common problem in modeling with NN’s. It happens when the accuracy is high on the training set, but low on the validation set; i.e., the model memorizes the characteristics of the training data. Common ways of handling this is adding regularization techniques such as L2 regularization and dropout, and/or early stopping and/or batch validation. If there is possibility of adding more input data either through data collection or data augmentation, it would yield better results. If the model architecture is too complex, one can try to simplify it as we did in our case. More complex LSTM models did not increase the validation accuracy thus, we went ahead with simpler model.

The optimal architecture and properties of the ordinary NN’s were as follows:

• 1. Has two hidden layers each with three hidden nodes;

• 2. Each of the hidden nodes use RELU activation function;

• 3. There is one output layer as we are trying to forecast one step ahead;

• 4. Learning rates are automatically optimized by the model in Keras;

• 5. The training, validation and test parts were divided as 70%, 10% and 20%.

Then we applied DNN’s of type LSTM to the datasets. The optimal properties of LSTM given are:

• 1. Has two hidden layers each with 300 hidden nodes;

• 2. Each of the hidden nodes use RELU activation function;

• 3. The number of output nodes are 3 as we are trying to forecast 3 steps ahead;

• 4. Learning rates are automatically optimized by the model in Keras;

• 5. The training validation and test parts were divided as 70%, 10% and 20%.

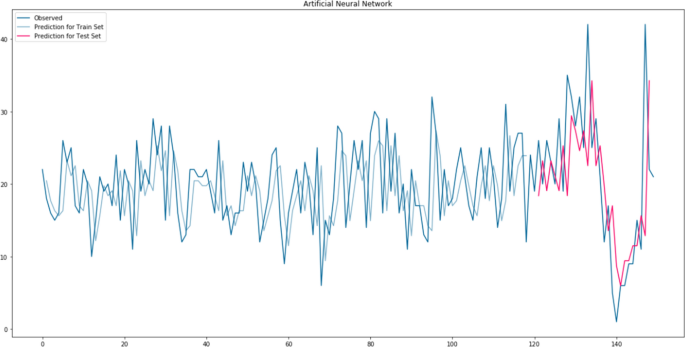
The training process aims to minimize the deviation between the desired and observed output values. Gradient Descent Algorithm was used to determine the direction of improvement during the training. The results show that DNN’s forecast the data very close to the actual values; Fig. 6 presents an example of this. In this dataset, the behavior of the time series is very different (i.e. more volatile) towards the end. Even though the model was trained with the smooth part of the data, DNN’s can perform well also in the test portion where the demand behavior is more volatile. The Root Mean Square Error (RMSE) is 9.35 for this dataset. Our findings confirm the results obtained by Oroojlooyjadid et al. (2018) that DNN’s work well in forecasting the nervous demand.

Fig. 6

The graph of forecasted vs actual values

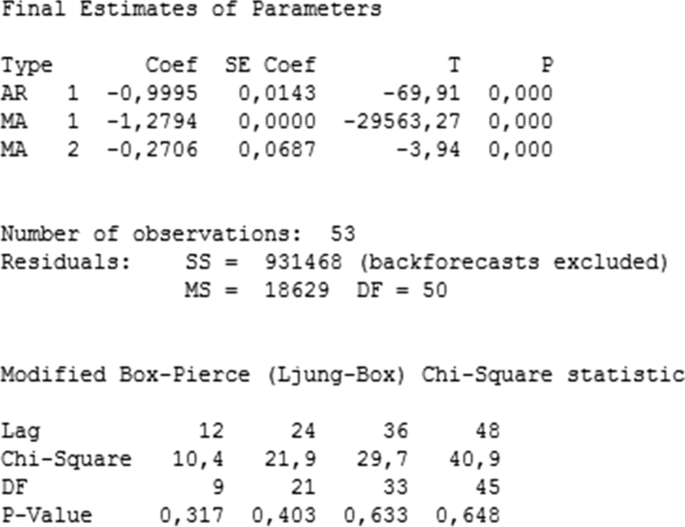
Next, we discuss the results obtained from traditional models (Fig. 7). We applied log transformation to have suitable ACF and PACF for the ARIMA model. ARIMA (1,0,2) was the best fitting forecast among all ARIMA (p,d,q) for our data. All the p-values for AR and MA coefficients are zero and p-values for the Box-Pierce Chi-Square statistic are greater than 5%.

Fig. 7

ARIMA test results for the main data

The problem with the ARIMA model is that the prediction intervals for the next periods are too large and thus, not much meaningful. Another point is that the AR coefficient is equal to 1 and the moving average component is not invertible. Croston’s method is one of the most famous models to forecast intermittent sales, however it contradicts with our main goal: we would like to see the periods with no order. Instead, Croston’s method distributes the total demand to all days and just smooths out intermittent demand. Grey prediction model was found to be not adequate in our case. The a value was − 0.98 and this caused the model to generate extremely high values for the next periods. Basically, this means an exponential increase in the cumulative forecasts. For example, for period 28, the cumulative forecasted was expressed in terms of e²⁸. This confirms that Grey models work with smaller samples (for example, with 5 or 6 data).

Best-fitting forecasting methods among traditional models were Moving Average (MA), Single Exponential Smoothing (SES) and Double Exponential Smoothing (DES). Table 3 summarizes the results for all datasets. MSE values have been in the range of 6.70–23.69. In general, it is difficult to find accurate forecasting models among traditional models for such sporadic demand data. In the second column of the table, the best fitting traditional model is given; the next columns are the MSE’s for the best fitting traditional model and the Deep Learning Model. NN’s performed better than traditional methods and dominated them for all datasets. The MSE values for LSTM models were in the range of 5.26–20.45, meaning 9% to 35% better results than best fitting traditional model. As expected, ordinary NN’s generated slightly better forecasts, thanks to the one-step-ahead outputs. LSTM’s were required to generate three-step-ahead predictions which made their task difficult. Ordinary NN’s generated 15% to 38% better forecasts than traditional models.

Table 3 Forecasting methods results (MSE)

On top of the MSE, we calculated Mean Absolute Error (MAE) to have a better picture of the accuracy of the different approaches.

We tried adding more hidden layers but adding more layers is not always yielding the expected results. There are contradicting results in the literature: some researchers have found that there are small improvements by adding new hidden layers, some have found that no actual improvement is observed [50]. In our case also, no evident improvements were observed,on the other hand, training the data became much more difficult.

4.2 Modeling online sales

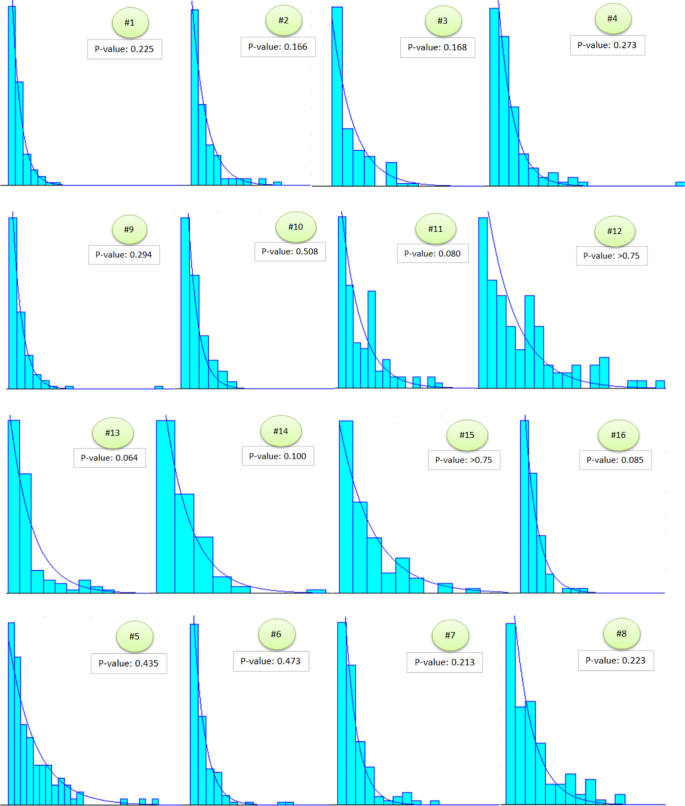
In this section, we discuss the proposed approach for modeling online sales. Figure 8 shows the distribution of order interarrival times for all 16 other stores. The p-values confirm that at 5% significance level, we fail to reject that the data come from Exponential distribution with respective parameters.

Fig. 8

Distribution test results for the order arrivals

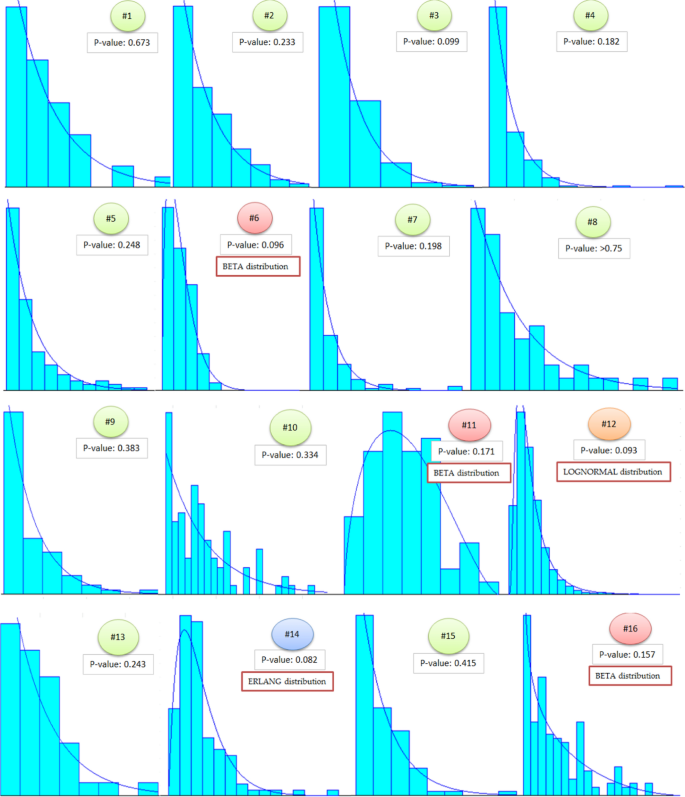
Then we conducted goodness-of-fit tests for the order sizes (Fig. 9). At 5% significance level, 11 stores appeared to follow Exponential distribution. The best fitting distribution for stores #6, #11 and #16 was Beta distribution. For stores #12 and #14, the best fitting distributions were Lognormal and Erlang, respectively. The reason for such deviations from Exponential distribution was that the sellers had fast-selling items in the intermediate intervals of the price range. For example, the store #12 had watches for sale which became favorite items among buyers, so we have more counts in the second bin of the histogram than in the first one.

Fig. 9

Distribution test results for the order sizes

Then, the Kolmogorov–Smirnov tests were conducted for the data by assuming α = 0.05 (Table 4). In the results tables, we have omitted the datasets that do not follow the Exponential distribution for both order sizes and order interarrival times since they need slightly different formulation.

Table 4 Forecasting methods results (MAE)

According to the table above, all input data have shown good fit with the proposed Poisson Exponential Distribution. In addition to the K-S test, we simulated order arrivals using the Poisson-Exponential distribution for 12 data sets that followed Exponential distribution for both the order interarrival times and order sizes. Simulations were done with 10 000 replications each, and the average values have been recorded. Two main parameters are total sales and days when order arrivals happen. Table 5 depicts the comparison between the real data and randomly generated data from the Poisson-Exponential distribution for the same period. We did not simulate the datasets 6, 11, 12, 14, and 16 since they do not follow the Poisson-Exponential distribution and need a different setup for the simulations.

Table 5 The K-S test results for the datasets

The accuracy in these parameters is in the range of 1–7%; showing the power of the Poisson Exponential distribution in modeling the intermittent online sales. The existing schemes have explored the application of the Neural Networks to other domains such as spare parts demand forecasting which is a well-known problem. In our case, we analyze both order interarrival times and order sizes, formulate the problem in terms of the Compound distributions, forecast the future sales by using DNN’s and provide their performance on real data from e-commerce platforms. The existing schemes have explored the application of the Neural Networks to other domains such as spare parts demand forecasting which is a well-known problem. The contribution of this paper is that we analyze both order interarrival times and order sizes, formulate the problem in terms of the Compound distributions, forecast the future sales by using DNN’s and provide their performance on real data from e-commerce platforms. This is a more specific application which is based on the needs and requirements of e-business operators.

5 Conclusion

In this paper, we discussed novel ways to forecast and model intermittent online sales by applying DNN’s and Compound distributions, respectively. The research task originated from a real-life situation faced by the online sellers. There conclusions for the two main problems are:

• (1) Forecasting online sales for different stores. The main finding is that Deep Learning models with two hidden layers dominate the traditional models in forecast accuracy.

• (2) Finding suitable distributions to model online sales. We found out that Poisson Exponential distribution can be used to model such sales in most of the cases.

We found out that LSTM models outperform traditional models for multi-step-ahead forecasting by up to 35%. For single step forecasts, ordinary NN’s can be used which generate up to 38% better forecasts than traditional models. Another finding of this article is that if the order arrival process is following Poisson distribution, DNN’s can be used for forecasting the future demand with higher accuracy than the traditional methods. In the modeling part, it was concluded that most of the time Poisson-Exponential distribution can be used to model intermittent online sales. We tested the distributions by using the Kolmogorov–Smirnov test and they showed good fit. These models can be used for many purposes such as simulating the sales process (Table 6).

Table 6 Simulation results

Advanced methods of Artificial Intelligence, including Deep Learning will present new possibilities for forecasting complex demand patterns. Good forecasts are needed for automated order replenishment and inventory control decisions. There will be required powerful algorithms to perform these tasks; and Deep Learning Models provide us this power as discussed by many authors in the literature. The algorithms will make forecasts, find distributions of the underlying demand/lead time data and will make decisions on how much to keep in stock, when to order, how much to order etc. This paper has demonstrated how applying DL models for forecasting online sales, especially intermittent ones; DNN’s can present a good potential in forecasting accuracy.

In this study, we used data mainly from individual sellers. In the future, the analysis should be extended to analyze the performance of high-volume selling items with complex patterns. Future research should attempt to use compound Poisson distribution with these to cover all the possible scenarios and to get a more accurate picture of the process. The data that we used from 17 online stores were selected to have low means and high standard deviations to analyze the intermittent sales patterns. As such they might not represent the whole e-business in general. It is evident that the stores with regular sales do not have intermittency in their demand and they can be modeled by using the Normal distribution most of the time. We have shown the use of DNN’s in time series; but recently we have seen the rise of generative AI tools such as ChatGPT and Bard. It would be interesting to study the possible applications of such systems in forecasting tasks of e-commerce.