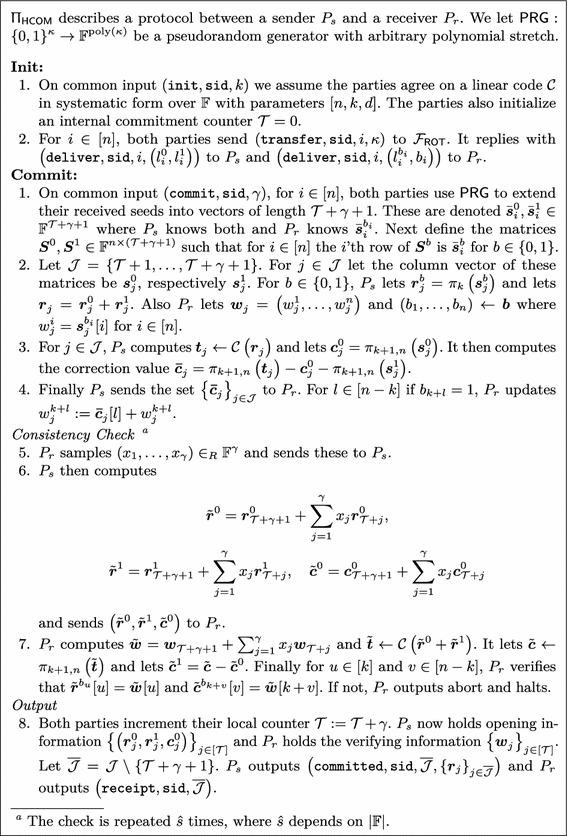On the Complexity of Additively Homomorphic UC Commitments

Abstract

We present a new constant round additively homomorphic commitment scheme with (amortized) computational and communication complexity linear in the size of the string committed to. Our scheme is based on the non-homomorphic commitment scheme of Cascudo et al. presented at PKC 2015. However, we manage to add the additive homomorphic property, while at the same time reducing the constants. In fact, when opening a large enough batch of commitments we achieve an amortized communication complexity converging to the length of the message committed to, i.e., we achieve close to rate 1 as the commitment protocol by Garay et al. from Eurocrypt 2014. A main technical improvement over the scheme mentioned above, and other schemes based on using error correcting codes for UC commitment, we develop a new technique which allows to based the extraction property on erasure decoding as opposed to error correction. This allows to use a code with significantly smaller minimal distance and allows to use codes without efficient decoding.

Our scheme only relies on standard assumptions. Specifically we require a pseudorandom number generator, a linear error correcting code and an ideal oblivious transfer functionality. Based on this we prove our scheme secure in the Universal Composability (UC) framework against a static and malicious adversary corrupting any number of parties.

On a practical note, our scheme improves significantly on the non-homomorphic scheme of Cascudo et al. Based on their observations in regards to efficiency of using linear error correcting codes for commitments we conjecture that our commitment scheme might in practice be more efficient than all existing constructions of UC commitment, even non-homomorphic constructions and even constructions in the random oracle model. In particular, the amortized price of computing one of our commitments is less than that of evaluating a hash function once.

The authors acknowledge support from the Danish National Research Foundation and The National Science Foundation of China (under the grant 61361136003) for the Sino-Danish Center for the Theory of Interactive Computation and from the Center for Research in Foundations of Electronic Markets (CFEM), supported by the Danish Strategic Research Council.

R. Trifiletti—Partially supported by the European Research Commission Starting Grant 279447.

1 Introduction

Commitment schemes are the digital equivalent of a securely locked box: it allows a sender $P_s$ to hide a secret from a receiver $P_r$ by putting the secret inside the box, sealing it, and sending the box to $P_r$. As the receiver cannot look inside we say that the commitment is hiding. As the sender is unable to change his mind as he has given the box away we say the commitment is also binding. These simple, yet powerful properties are needed in countless cryptographic protocols, especially when guaranteeing security against a malicious adversary who can arbitrarily deviate from the protocol at hand. In the stand-alone model, commitment schemes can be made very efficient, both in terms of communication and computation and can be based entirely on the existence of one-way functions. These can e.g. be constructed from cheap symmetric cryptography such as pseudorandom generators [Nao90].

In this work we give an additively homomorphic commitment scheme secure in the UC-framework of [Can01], a model considering protocols running in a concurrent and asynchronous setting. The first UC-secure commitment schemes were given in [CF01, CLOS02] as feasibility results, while in [CF01] it was also shown that UC-commitments cannot be instantiated in the standard model and therefore require some form of setup assumption, such as a CRS. Moreover a construction for UC-commitments in such a model implies public-key cryptography [DG03]. Also, in the UC setting the previously mentioned hiding and binding properties are augmented with the notions of equivocality and extractability, respectively. These properties are needed to realize the commitment functionality we introduce later on. Loosely speaking, a scheme is equivocal if a single commitment can be opened to any message using special trapdoor information. Likewise a scheme is extractable if from a commitment the underlying message can be extracted efficiently using again some special trapdoor information.

Based on the above it is not surprising that UC-commitments are significantly less efficient than constructions in the stand-alone model. Nevertheless a plethora of improvements have been proposed in the literature, e.g.  [DN02, NFT09, Lin11, BCPV13, Fuj14, CJS14] considering different number theoretic hardness assumptions, types of setup assumption and adversarial models. Until recently, the most efficient schemes for the adversarial model considered in this work were that of [Lin11, BCPV13] in the CRS model and [HMQ04, CJS14] in different variations of the random oracle model [BR93].

Related Work. In [GIKW14] and independently in [DDGN14] it was considered to construct UC-commitments in the OT-hybrid model and at the same time confining the use of the OT primitive to a once-and-for-all setup phase. After the setup phase, the idea is to only use cheap symmetric primitives for each commitment thus amortizing away the cost of the initial OTs. Both approaches strongly resembles the “MPC-in-the-head” line of work of [IKOS07, HIKN08, IPS08] in that the receiver is watching a number of communication channels not disclosed to the sender. In order to cheat meaningfully in this paradigm the sender needs to cheat in many channels, but since he is unaware where the receiver is watching he will get caught with high probability. Concretely these schemes build on VSS and allow the receiver to learn an unqualified set of shares for a secret s. However the setup is such that the sender does not know which unqualified set is being “watched”, so when opening he is forced to open to enough positions with consistent shares to avoid getting caught. The scheme of [GIKW14] focused primarily on the rate of the commitments in an asymptotic setting while [DDGN14] focused on the computational complexity. Furthermore the secret sharing scheme of the latter is based on Reed-Solomon codes and the scheme achieved both additive and multiplicative homomorphisms.

The idea of using OTs and error correction codes to realize commitments was also considered in [FJN+13] in the setting of two-party secure computation using garbled circuits. Their scheme also allowed for additively homomorphic operations on commitments, but requires a code with a specific privacy property. The authors pointed to [CC06] for an example of such a code, but it turns out this achieves quite low constant rate due to the privacy restriction. Care also has to be taken when using this scheme, as binding is not guaranteed for all committed messages. The authors capture this by allowing some message to be “wildcards”. However, in their application this is acceptable and properly dealt with.

Finally in [CDD+15] a new approach to the above OT watch channel paradigm was proposed. Instead of basing the underlying secret sharing scheme on a threshold scheme the authors proposed a scheme for a particular access structure. This allowed realization of the scheme using additive secret sharing and any linear code, which achieved very good concrete efficiency. The only requirement of the code is that it is linear and the minimum distance is at least $2{s} +1$ for statistical security ${s}$. To commit to a message m it is first encoded into a codeword c. Then each field element $c_i$ of c is additively shared into two field elements $c_i^0$ and $c_i^1$ and the receiver learns one of these shares via an oblivious transfer. This in done in the watch-list paradigm where the same shares $c_i^0$ are learned for all the commitments, by using the OTs only to transfer short seeds and then masking the share $c_i^0$ and $c_i^1$ for all commitments from these pairs of seeds. This can be seen as reusing an idea ultimately going back to [Kil88, CvT95]. Even if the adversary commits to a string $c'$ which is not a codeword, to open to another message, it would have to guess at least s of the random choice bits of the receiver. Furthermore the authors propose an additively homomorphic version of their scheme, however at the cost of using VSS which imposes higher constants than their basic non-homomorphic construction.

Motivation. As already mentioned, commitment schemes are extremely useful when security against a malicious adversary is required. With the added support for additively homomorphic operations on committed values even more applications become possible. One is that of maliciously secure two-party computation using the LEGO protocols of [NO09, FJN+13, FJNT15]. These protocols are based on cut-and-choose of garbled circuits and require a large amount of homomorphic commitments, in particular one commitment for each wire of all garbled gates. In a similar fashion the scheme of [AHMR15] for secure evaluation of RAM programs also make use of homomorphic commitments to transform garbled wire labels of one garbled circuit to another. Thus any improvement in the efficiency of homomorphic commitments is directly transferred to the above settings as well.

Fig. 1.

Ideal functionality $\mathcal {F} _{\textsf {ROT}}$.

Our Contribution. We introduce a new, very efficient, additively homomorphic UC-secure commitment scheme in the $\mathcal {F} _{\textsf {ROT}}$-hybrid model. The $\mathcal {F} _{\textsf {ROT}}$-functionality is fully described in Fig. 1. Our scheme shows that:

• 1. The asymptotic complexity of additively homomorphic UC commitment is the same as the asymptotic complexity of non-homomorphic UC commitment, i.e., the achievable rate is $1-o(1)$. In particular, the homomorphic property comes for free.

• 2. In addition to being asymptotically optimal, our scheme is also more practical (smaller hidden constants) than any other existing UC commitment scheme, even non-homomorphic schemes and even schemes in the random oracle model.

In more detail our main contributions are as follows:

• We improve on the basic non-homomorphic commitment scheme of [CDD+15] by reducing the requirement of the minimum distance of the underlying linear code from $2{s} +1$ to ${s}$ for statistical security ${s}$. At the same time our scheme becomes additively homomorphic, a property not shared with the above scheme. This is achieved by introducing an efficient consistency check at the end of the commit phase, as described now. Assume that the corrupted sender commits to a string $c'$ which has Hamming distance 1 to some codeword $c_0$ encoding message $m_0$ and has Hamming distance $s-1$ to some other codeword $c_1$ encoding message $m_1$. For both the scheme in [CDD+15] and our scheme this means the adversary can later open to $m_0$ with probability $\frac{1}{2}$ and to $m_1$ with probability $2^{-s+1}$. Both of these probabilities are considered too high as we want statistical security $2^{-s}$. So, even if we could decode $c'$ to for instance $m_0$, this might not be the message that the adversary will open to later. It is, however, the case that the adversary cannot later open to both $m_0$ and $m_1$, except with probability $2^{-s}$ as this would require guessing s of the random choice bits. The UC simulator, however, needs to extract which of $m_0$ and $m_1$ will be opened to already at commitment time. We introduce a new consistency check where we after the commitment phase ask the adversary to open a random linear combination of the committed purported codewords. This linear combination will with overwhelming probability in a well defined manner “contain” information about every dirty codeword $c'$ and will force the adversary to guess some of the choice bits to successfully open it to some close codeword c. The trick is then that the simulator can extract which of the choice bits the adversary had to guess and that if we puncture the code and the committed strings at the positions at which the adversary guessed the choice bits, then the remaining strings can be proven to be codewords in the punctured code. Since the adversary guesses at most $s-1$ choice bits, except with negligible probability $2^{-s}$ we only need to puncture $s-1$ positions, so the punctured code still has distance 1. We can therefore erasure decode and thus extract the committed message. If the adversary later open to another message he will have to guess additional choice bits, bringing him up to having guessed at least s choice bits. With the minimal distance lowered the required code length is also reduced and therefore also the amount of required initial OTs. As an example, for committing to messages of size $k = 256$ with statistical security ${s} =40$ this amounts to roughly 33 % less initial OTs than required by [CDD+15].

• We furthermore propose a number of optimizations that reduce the communication complexity by a factor of 2 for each commitment compared to [CDD+15] (without taking into account the smaller code length required). We give a detailed comparison to the schemes of [Lin11, BCPV13, CJS14] and [CDD+15] in Sect. 4 and show that for the above setting with $k = 256$ and ${s} =40$ our new construction outperforms all existing schemes in terms of communication if committing to 304 messages or more while retaining the computational efficiency of [CDD+15]. This comparison includes the cost of the initial OTs. If committing to 10,000 messages or more we see the total communication is around of [BCPV13], around of the basic scheme of [CDD+15] and around of the homomorphic version.

• Finally we give an extension of any additively homomorphic commitment scheme that achieves an amortized rate close to 1 in the opening phase. Put together with our proposed scheme and breaking a long message into many smaller blocks we achieve rate close to 1 in both the commitment and open phase of our protocol. This extension is interactive and is very similar in nature to the introduced consistency check for decreasing the required minimum distance. Although based on folklore techniques this extension allows for very efficiently homomorphic commitment to long messages without requiring correspondingly many OTs.

2 The Protocol

We use $\kappa$ and ${s}$ to denote the computational and statistical security parameter respectively. This means that for any fixed ${s}$ and any polynomial time bounded adversary, the advantage of the adversary is $2^{-{s}} + {\text {negl}}(\kappa )$ for a negligible function ${\text {negl}}$. i.e., the advantage of any adversary goes to $2^{-{s}}$ faster than any inverse polynomial in the computational security parameter. If ${s} = \varOmega (\kappa )$ then the advantage is negligible. We will be working over an arbitrary finite field ${\mathbb {F}}$. Based on this, along with ${s}$, we define $\hat{s} = \lceil {s}/ \log _2(|{\mathbb {F}}|)\rceil$.

We will use as shorthand $[n] = {{\left\{ 1,2,\ldots ,n \right\} }}$, and $e \in _R S$ to mean: sample an element e uniformly at random from the set S. When $\varvec{r}$ and $\varvec{m}$ are vectors we write $\varvec{r} \Vert \varvec{m}$ to mean the vector that is the concatenation of $\varvec{r}$ and $\varvec{m}$. We write $y {\leftarrow } P(x)$ to mean: perform the (potentially randomized) procedure P on input x and store the output in variable y. We will use $x:=y$ to denote an assignment of x to y. We will interchangeably use subscript and bracket notation to denote an index of a vector, i.e. $x_i$ and $\varvec{x}[i]$ denotes the i’th entry of a vector $\varvec{x}$ which we will always write in bold. Furthermore we will use $\pi _{i,j}$ to denote a projection of a vector that extracts the entries from index i to index j, i.e. $\pi _{i,j}{{\left( \varvec{x} \right) }} = {{\left( x_i,x_{i+1},\ldots ,x_{j} \right) }}$. We will also use $\pi _l{{\left( \varvec{x} \right) }}=\pi _{1, l}{{\left( \varvec{x} \right) }}$ as shorthand to denote the first l entries of $\varvec{x}$.

In Fig. 2 we present the ideal functionality $\mathcal {F} _{\textsf {HCOM}}$ that we UC-realize in this work. The functionality differs from other commitment functionalities in the literature by only allowing the sender $P_s$ to decide the number of values he wants to commit to. The functionality then commits him to random values towards a receiver $P_r$ and reveals the values to $P_s$. The reason for having the functionality commit to several values at a time is to reflect the batched nature of our protocol. That the values committed to are random is a design choice to offer flexibility for possible applications. In Appendix  Awe show an efficient black-box extension of $\mathcal {F} _{\textsf {HCOM}}$ to chosen-message commitments.

2.1 Protocol $\Pi _{\textsf {HCOM}}$

Our protocol $\Pi _{\textsf {HCOM}}$ is cast in the $\mathcal {F} _{\textsf {ROT}}$-hybrid model, meaning the parties are assumed access to the ideal functionality $\mathcal {F} _{\textsf {ROT}}$ in Fig. 1. The protocol UC-realizes the functionality $\mathcal {F} _{\textsf {HCOM}}$ and is presented in full in Figs. 4 and 5. At the start of the protocol a once-and-for-all Init step is performed where $P_s$ and $P_r$ only need to know the size of the committed values $k$ and the security parameters. We furthermore assume that the parties agree on a $[{n}, k, {d} ]$ linear code $\mathcal {C}$ in systematic form over the finite field ${\mathbb {F}}$ and require that the minimum distance ${d} \ge {s}$ for statistical security parameter s. The parties then invoke n copies of the ideal functionality $\mathcal {F} _{\textsf {ROT}}$ with the computational security parameter $\kappa$ as input, such that $P_s$ learns ${n}$ pairs of $\kappa$-bit strings ${l}_{i}^{0}, {l}_{i}^{1}$ for $i \in [{n} ]$, while $P_r$ only learns one string of each pair. In addition to the above the parties also introduce a commitment counter $\mathcal {T}$ which simply stores the number of values committed to. Our protocol is phrased such that multiple commitment phases are possible after the initial ROTs have been performed, and the counter is simply incremented accordingly.

Next a Commit phase is described where at the end, $P_s$ is committed to $\gamma$ pseudorandom values. The protocol instructs the parties to expand the previously learned $\kappa$-bit strings, using a pseudorandom generator PRG, into ${\bar{\varvec{s}}}_{i}^{b} \in {\mathbb {F}}^{\mathcal {T} + \gamma +1}$ for $b \in {\{0,1\}}$ and $i \in [{n} ]$. The reason for the extra length will be apparent later. We denote by $\mathcal {J} = {{\left\{ \mathcal {T} +1,\ldots ,\mathcal {T} +\gamma +1 \right\} }}$ the set of indices of the $\gamma +1$ commitments being setup in this invocation of Commit. After the expansion $P_s$ knows all of the above $2{n}$ row-vectors, while $P_r$ only knows half. The parties then view these row-vectors as matrices $\varvec{S}^0$ and $\varvec{S}^1$ where row i of $\varvec{S}^b$ consists of the vector ${\bar{\varvec{s}}}_{i}^{b}$. We let ${\varvec{s}}_{j}^{b} \in {\mathbb {F}}^{n}$ denote the j’th column vector of the matrix $\varvec{S}^b$ for $j \in \mathcal {J}$. These column vectors now determine the committed pseudorandom values, which we define as ${\varvec{r}}_{j}^{} = {\varvec{r}}_{j}^{0} + {\varvec{r}}_{j}^{1}$ where ${\varvec{r}}_{j}^{b} = \pi _{k}({\varvec{s}}_{j}^{b})$ for $j \in \mathcal {J}$. The above steps are also pictorially described in Fig. 3.

Fig. 2.

Ideal functionality $\mathcal {F} _{\textsf {HCOM}}$.

Fig. 3.

On the left hand side we see how the initial part of the Commit phase of $\Pi _{\textsf {HCOM}}$ is performed by $P_s$ when committing to $\gamma$ messages. On the right hand side we look at a single column of the two matrices $\varvec{S}^0,\varvec{S}^1$ and how they define the codeword ${\varvec{t}}_{j}^{}$ for column $j \in \mathcal {J}$, where $\mathcal {J} = {{\left\{ \mathcal {T} +1,\ldots ,\mathcal {T} +\gamma +1 \right\} }}$.

The goal of the commit phase is for $P_r$ to hold one out of two shares of each entry of a codeword of $\mathcal {C}$ that encodes the vector ${\varvec{r}}_{j}^{}$ for all $j \in \mathcal {J}$. At this point of the protocol, what $P_r$ holds is however not of the above form. Though, because the code is in systematic form we have by definition that $P_r$ holds such a sharing for the first $k$ entries of each of these codewords. To ensure the same for the rest of the entries, for all $j \in \mathcal {J}$, $P_s$ computes ${\varvec{t}}_{j}^{} {\leftarrow } \mathcal {C} ({\varvec{r}}_{j}^{})$ and lets ${\varvec{c}}_{j}^{0} = \pi _{k +1,{n}}({\varvec{s}}_{j}^{0})$. It then computes the correction value ${\varvec{\bar{c}}}_{j}^{} = \pi _{k +1,{n}}({\varvec{t}}_{j}^{}) - {\varvec{c}}_{j}^{0} - \pi _{k +1,{n}}({\varvec{s}}_{j}^{1})$ and sends this to $P_r$. Figure 3 also gives a quick overview of how these vectors are related.

Fig. 4.

Protocol $\Pi _{\textsf {HCOM}}$ UC-realizing $\mathcal {F} _{\textsf {HCOM}}$ in the $\mathcal {F} _{\textsf {ROT}}$-hybrid model – part 1.

When receiving the correction value ${\varvec{\bar{c}}}_{j}^{}$, we notice that for the columns ${\varvec{s}}_{j}^{0}$ and ${\varvec{s}}_{j}^{1}$, $P_r$ knows only the entries $w_j^i = {\varvec{s}}_{j}^{b_i} [i]$ where $b_i$ is the choice-bit it received from $\mathcal {F} _{\textsf {ROT}}$ in the i’th invocation. For all $l \in [{n}-k ]$, if $b_{k +l} = 1$ it is instructed to update its entry as follows:

$$\begin{aligned} {w}_{j}^{k +l} := {\varvec{\bar{c}}}_{j}^{} [l] + {w}_{j}^{k +l} = {\varvec{t}}_{j}^{} [k +l] - {\varvec{c}}_{j}^{0} [l] - {\varvec{s}}_{j}^{1} [k +l] + {w}_{j}^{k +l} = {\varvec{t}}_{j}^{} [k +l] - {\varvec{c}}_{j}^{0} [l]\ . \end{aligned}$$

Due to the above corrections, it is now the case that for all $l \in [{n}-k ]$ if $b_{k +l} = 0$, then ${w}_{j}^{k +l} = {\varvec{c}}_{j}^{0} [l]$ and if $b_{k +l} = 1$, ${w}_{j}^{k +l} = {\varvec{t}}_{j}^{} [k +l] - {\varvec{c}}_{j}^{0} [l]$. This means that at this point, for all $j \in \mathcal {J}$ and all $i \in [{n} ]$, $P_r$ holds exactly one out of two shares for each entry of the codeword ${\varvec{t}}_{j}^{}$ that encodes the vector ${\varvec{r}}_{j}^{}$.

The Open procedure describes how $P_s$ can open to linear combinations of previously committed values. We let C be the indices to be opened and $\alpha _c$ for $c \in C$ be the corresponding coefficients. The sender then computes ${\varvec{r}}_{}^{0} = \sum _{c \in C} \alpha _c \cdot {\varvec{r}}_{c}^{0}$, ${\varvec{r}}_{}^{1} = \sum _{c \in C} \alpha _c \cdot {\varvec{r}}_{c}^{1}$, and ${\varvec{c}}_{}^{0} = \sum _{c \in C} \alpha _c \cdot {\varvec{c}}_{c}^{0}$ and sends these to $P_r$. When receiving the three values, the receiver computes the codeword ${\varvec{t}}_{}^{} {\leftarrow } \mathcal {C} ({\varvec{r}}_{}^{0} +{\varvec{r}}_{}^{1})$ and from ${\varvec{c}}_{}^{0}$ and $\varvec{t}$ it computes ${\varvec{c}}_{}^{1}$. It also computes ${\varvec{w}}_{}^{} = \sum _{c \in C} \alpha _c \cdot {\varvec{w}}_{c}^{}$ and verifies that ${\varvec{r}}_{}^{0},{\varvec{r}}_{}^{1},{\varvec{c}}_{}^{0}$, and ${\varvec{c}}_{}^{1}$ are consistent with these. If everything matches it accepts ${\varvec{r}}_{}^{0} +{\varvec{r}}_{}^{1}$ as the value opened to.

If the sender $P_s$ behaves honestly in Commit of $\Pi _{\textsf {HCOM}}$, then the scheme is UC-secure as it is presented until now. In fact it is also additively homomorphic due to the linearity of the code $\mathcal {C}$ and the linearity of additive secret sharing. However, this only holds because $P_r$ holds shares of valid codewords. If we consider a malicious corruption of $P_s$, then the shares held by $P_r$ might not be of valid codewords, and then it is undefined at commitment time what the value committed to is.

Fig. 5.

Protocol $\Pi _{\textsf {HCOM}}$ UC-realizing $\mathcal {F} _{\textsf {HCOM}}$ in the $\mathcal {F} _{\textsf {ROT}}$-hybrid model – part 2.

2.2 Optimizations over [CDD+15]

The work of [CDD+15] describes two commitment schemes, a basic and a homomorphic version. For both schemes therein the above issue of sending correct shares is handled by requiring the underlying code $\overline{\mathcal {C}}$ with parameters $[\overline{{n}}, k, \overline{{d}}]$ to have minimum distance $\overline{{d}} \ge 2{s} +1$, as then the committed values are always defined to be the closest valid codewords of the receivers shares. This is however not enough to guarantee binding when allowing homomorphic operations. To support this, the authors propose a version of the scheme that involves the sender $P_s$ running a “MPC-in-the-head” protocol based on a verifiable secret sharing scheme of which the views of the simulated parties must be sent to $P_r$.

Up until now the scheme we have described is very similar to the basic scheme of [CDD+15]. The main difference is the use of $\mathcal {F} _{\textsf {ROT}}$ as a starting assumption instead of $\mathcal {F} _{\textsf {OT}}$ and the way we define and send the committed value corrections. In [CDD+15] the corrections sent are for both the 0 and the 1 share. This means they send $2\overline{{n}}$ field elements for each commitment in total. Having the code in systematic form implies that for all $j \in \mathcal {J}$ and $i \in [k ]$ the entries ${\varvec{w}}_{j}^{i}$ are already defined for $P_r$ as part of the output of the PRG, thus saving $2k$ field elements of communication per commitment. Together with only sending corrections to the 1-share, we only need to send ${n}-k$ field elements as corrections. Meanwhile this only commits the sender to a pseudorandom value, so to commit to a chosen value another correction of $k$ elements needs to be sent. In total we therefore save a factor 2 of communication from these optimizations.

However the main advantage of our approach comes from ensuring that the shares held by $P_r$ binds the sender $P_s$ to his committed value, while only requiring a minimum distance of ${s}$. On top of that our approach is also additively homomorphic. The idea is that $P_r$ will challenge $P_s$ to open a random linear combination of all the committed values and check that these are valid according to $\mathcal {C}$. Recall that $\gamma +1$ commitments are produced in total. The reason for this is to guarantee hiding for the commitments, even when $P_r$ learns a random linear combination of them. Therefore, the linear combination is “blinded” by a pseudorandom value only used once and thus it appears pseudorandom to $P_r$ as well. This consistency check is sufficient if $|{\mathbb {F}}|^{-1} \le 2^{-{s}}$, however if the field is too small then the check is simply repeated times such that $|{\mathbb {F}}|^{-\hat{s}} \le 2^{-{s}}$. In total this approach requires setting up commitments to $\hat{s}$ additional values for each invocation of Commit.

The intuition why the above approach works is that if the sender $P_s$ sends inconsistent corrections, it will get challenged on these positions with high probability. In order to pass the check, $P_s$ must therefore guess which choice-bit $P_r$ holds for each position for which it sent inconsistent values. The challenge therefore forces $P_s$ to make a decision at commitment time which underlying value to send consistent openings to, and after that it can only open to that value successfully. In fact, the above approach also guarantees that the scheme is homomorphic. This is because all the freedom $P_s$ might have had by sending maliciously constructed corrections is removed already at commitment time for all values, so after this phase commitments and shares can be added together without issue.

To extract all committed values when receiving the opening to the linear combination the simulator identifies which rows of $\varvec{S}^0$ and $\varvec{S}^1$ $P_s$ is sending inconsistent shares for. For these positions it inserts erasures in all positions of ${\varvec{t}}_{j}^{}$ (as defined by $\varvec{S}^0, \varvec{S}^1, {\varvec{\tilde{c}}}_{j}^{}$ and $\mathcal {C}$). As there are at most ${s}-1$ positions where $P_s$ could have cheated and the distance of the linear code is $d \ge {s}$ the simulator can erasure decode all columns to a unique value, and this is the only value $P_s$ can successfully open to.¹

2.3 Protocol Extension

The protocol $\Pi _{\textsf {HCOM}}$ implements a commitment scheme where the sender commits to pseudorandom values. In many applications however it is needed to commit to chosen values instead. It is know that for any UC-secure commitment scheme one can easily turn a commitment from a random value into a commitment of a chosen one using the random value as a one-time pad encryption of the chosen value. For completeness, in Appendix A, we show this extension for any protocol implementing $\mathcal {F} _{\textsf {HCOM}}$.

In addition we also highlight that all additively homomorphic commitment schemes support the notion of batch-opening. For applications where a large amount of messages need to be opened at the same time this has great implications on efficiency. The technique is roughly that $P_s$ sends the values he wants to open directly to $P_r$. To verify correctness the receiver then challenges the sender to open to $\hat{s}$ random linear combinations of the received messages. For the same reason as for the consistency check of Commit this optimization retains binding. Using this method the overhead of opening the commitments is independent of the number of messages opened to and therefore amortizes away in the same manner as the consistency check and the initial OTs. However this way of opening messages has the downside of making the opening phase interactive, which is not optimal for all applications. See Appendix A for details.

The abovementioned batch-opening technique also has applicability when committing to large messages. Say we want to commit to a message m of length M. The naive approach would be to instantiate our scheme using a $[n_M,M,{s} ]$ code. However this would require $n_M \ge M$ initial OTs and in addition only achieve rate in the opening phase. Instead of the above, the idea is to break the large message of length M into blocks of length l for $l << M$. There will now be of these blocks in total. We then instantiate our scheme with a $[n_s, l, {s} ]$ code and commit to m in blocks of size l. When required to open we use the above-mentioned batch-opening to open all N blocks of m. It is clear that the above technique remains additively homomorphic for commitments to the large messages. In [GIKW14] they show an example for messages of size $2^{30}$ where they achieve rate $1.046^{-1} \approx 0.95$ in both the commit and open phase. In Appendix A we apply our above approach to the same setting and conclude that in the commit phase we achieve rate $\approx 0.974$ and even higher in the opening phase. This is including the cost of the initial OTs.

3 Security

In this section we prove the following theorem.

Theorem 1

The protocol $\Pi _{\textsf {HCOM}}$ in Figs. 4 and 5 UC-realizes the $\mathcal {F} _{\textsf {HCOM}}$ functionality of Fig. 2 in the $\mathcal {F} _{\textsf {ROT}}$-hybrid model against any number of static

Proof

We prove security for the case with a dummy adversary, so that the simulator is outputting simulated values directly to the environment and is receiving inputs directly from the environment. We focus on the case with one call to Commit. The proof trivially lifts to the case with multiple invocations. The case with two static corruptions is trivial. The case with no corruptions follows from the case with a corrupted receiver, as in the ideal functionality $\mathcal {F} _{\textsf {HCOM}}$ the adversary is given all values which are given to the receiver, so one can just simulate the corrupted receiver and then output only the public transcript of the communication to the environment. We now first prove the case with a corrupted receiver and then the case with a corrupted sender.

Assume that $P_r$ is corrupted. We use $\breve{P_r}$ to denote the corrupted receiver. This is just a mnemonic pseudonym for the environment $\mathcal {Z}$. The main idea behind the simulation is to simply run honestly until the opening phase. In the opening phase we then equivocate the commitment to the value received from the ideal functionality $\mathcal {F} _{\textsf {HCOM}}$ by adjusting the bits $\bar{\varvec{s}}_j^{1-b_i}$ not being watched by the receiver. This will be indistinguishable from the real world as the vectors $\bar{\varvec{s}}_i^{1-b_i}$ are indistinguishable from uniform in the view of $\breve{P_r}$ and if all the vectors $\bar{\varvec{s}}_i^{1-b_i}$ were uniform, then adjusting the bits not watched by $\breve{P_r}$ would be perfectly indistinguishable.

We first describe how to simulate the protocol without the step Consistency Check. We then discuss how to extend the simulation to this case.

The simulator $\mathcal {S}$ will run Init honestly, simulating $\mathcal {F} _{\textsf {ROT}}$ to $\breve{P_r}$. It then runs Commit honestly. On input ${{\left( {\texttt {opened}}, {\texttt {sid}}, {{\left\{ {{\left( c, \alpha _c \right) }} \right\} }}_{c\in C}, {\varvec{r}}_{}^{} \right) }}$ it must simulate an opening.

In the simulation we use the fact that in the real protocol $P_r$ can recompute all the values received from $P_s$ given just the value $\varvec{r}$ and the values $\varvec{w}_c$, which it already knows, and assuming that the checks ${\varvec{r}}_{}^{b_i} [i] = {\varvec{w}}_{}^{} [i]$ and ${\varvec{c}}_{}^{b_{k +l}} [l] = {\varvec{w}}_{}^{} [k +l]$ at the end of Fig. 5 are true. This goes as follows: First compute ${\varvec{w}}_{}^{} = \sum _{c \in C} \alpha _c \cdot {\varvec{w}}_{c}^{}$, ${\varvec{t}}_{}^{} = \mathcal {C} {{\left( {\varvec{r}}_{}^{} \right) }}$ and $\varvec{c} = \pi _{k+1,n}(\varvec{t})$, as in the protocol. Then for $i \in [k]$ and $l \in [{n}-k ]$ define

$$\begin{aligned} {\varvec{r}}_{}^{b_i} [i] = {\varvec{w}}_{}^{} [i]\ ,\ {\varvec{c}}_{}^{b_{k +l}} [l] = {\varvec{w}}_{}^{} [k +l]\ . \end{aligned}$$

(1)

$$\begin{aligned} {\varvec{r}}_{}^{1-b_i} [i] = {\varvec{r}}_{}^{} [i] - {\varvec{r}}_{}^{b_i} [i] \ ,\ {\varvec{c}}_{}^{1-b_{k +l}} [l] = {\varvec{c}}_{}^{} [l] - {\varvec{c}}_{}^{b_{k +l}} [l]\ . \end{aligned}$$

(2)

In (1) we use that the checks are true. In (2) we use that $\varvec{r} = \varvec{r}^0 + \varvec{r}^1$ and $\varvec{c}^1 = \varvec{c} - \varvec{c}^0$ by construction of $P_r$. This clearly correctly recomputes $(\varvec{r}^0, \varvec{r}^1, \varvec{c}^0)$.

On input ${{\left( {\texttt {opened}}, {\texttt {sid}}, {{\left\{ {{\left( c, \alpha _c \right) }} \right\} }}_{c\in C}, {\varvec{r}}_{}^{} \right) }}$ from $\mathcal {F} _{\textsf {HCOM}}$, the simulator will compute $(\varvec{r}^0, \varvec{r}^1, \varvec{c}^0)$ from $\varvec{r}$ and the values $\varvec{w}_c$ known by $\breve{P_r}$ as above and send ${{\left( {\texttt {opening}}, {{\left\{ c, \alpha _c \right\} }}_{c\in C}, {{\left( {\varvec{r}}_{}^{0}, {\varvec{r}}_{}^{1},{\varvec{c}}_{}^{0} \right) }} \right) }}$ to $\breve{P_r}$.

We now argue that the simulation is computationally indistinguishable from the real protocol. We go via two hybrids.

We define Hybrid I as follows. Instead of computing the rows $\bar{\varvec{s}}^{1-b_i}_i$ from the seeds $l^{1-b_i}_i$ the simulator samples $\bar{\varvec{s}}^{1-b_i}_i$ uniformly at random of the same length. Since $\breve{P_r}$ never sees the seeds $l^{1-b_i}_i$ and $P_s$ only uses them as input to PRG, we can show that the view of $\breve{P_r}$ in the simulation and Hybrid I are computationally indistinguishable by a black box reduction to the security of PRG.

We define Hybrid II as follows. We start from the real protocol, but instead of computing the rows $\bar{\varvec{s}}^{1-b_i}_i$ from the seeds $l^{1-b_i}_i$ we again sample $\bar{\varvec{s}}^{1-b_i}_i$ uniformly at random of the same length. As above, we can show that the view of $\breve{P_r}$ in the protocol and Hybrid II are computationally indistinguishable.

The proof then concludes by transitivity of computational indistinguishability and by observing that the views of $\breve{P_r}$ in Hybrid I and Hybrid II are perfectly indistinguishable. The main observation needed for seeing this is that in Hybrid I all the bits $\varvec{r}_j[i]$ are chosen uniformly at random and independently by $\mathcal {F} _{\textsf {HCOM}}$, whereas in Hybrid II they are defined by $\varvec{r}_j[i] = \varvec{r}^0_j[i] + \varvec{r}^1_j[i] = \varvec{r}^{b_i}_j[i] + \varvec{r}^{1-b_i}_j[i]$, where all the bits $\varvec{r}^{1-b_i}_j[i]$ are chosen uniformly at random and independently by $\mathcal {S}$. This yields the same distributions of the values $\varvec{r}_j$. All other value clearly have the same distribution.

We now address the step Consistency Check. The simulation of this step follows the same pattern as above. Define $\tilde{\varvec{r}} = \tilde{\varvec{r}}^0 + \tilde{\varvec{r}}^1$. This is the value from which $\tilde{\varvec{t}}$ is computed in Step 7 in Fig. 4. In the simulation and Hybrid I, instead pick $\tilde{\varvec{r}}$ uniformly at random and then recompute the values sent to $\breve{P_r}$ as above. In Hybrid II compute $\tilde{\varvec{r}}$ as in the protocol (but still starting from the uniformly random $\bar{\varvec{s}}^{1-b_i}_i$). Then simply observe that $\tilde{\varvec{r}}$ has the same distribution in Hybrid I and Hybrid II. In Hybrid I it is uniformly random. In Hybrid II it is computed as $\tilde{\varvec{r}}^0 + \tilde{\varvec{r}}^1 = ({\varvec{r}}_{\mathcal {T} +\gamma +1}^{0} + {\varvec{r}}_{\mathcal {T} +\gamma +1}^{1}) + \sum _{j=1}^\gamma x_j\varvec{r}_{\mathcal {T} +j}$, and it is easy to see that ${\varvec{r}}_{\mathcal {T} +\gamma +1}^{0} + {\varvec{r}}_{\mathcal {T} +\gamma +1}^{1}$ is uniformly random and independent of all other values in the view of $\breve{P_r}$.

We now consider the case where the sender is corrupted who we denote $\breve{P_s}$. The simulator will run the code of $P_s$ honestly, simulating also $\mathcal {F} _{\textsf {ROT}}$ honestly. It will record the values $(b_i, l^0_i, l^1_i)$ from Init. The remaining job of the simulator is then to extract the values ${\tilde{\varvec{r}}}_j$ to send to $\mathcal {F} _{\textsf {HCOM}}$ in the command . This should be done such that the probability that the receiver later outputs $({\texttt {opened}}, {\texttt {sid}}, \{ (c, \alpha _c) \}_{c \in C}, \varvec{r})$ for $\varvec{r} \ne \sum _{c \in C} \alpha _c {\tilde{\varvec{r}}}_c$ is at most $2^{-s}$. We first describe how to extract the values ${\tilde{\varvec{r}}}_j$ and then show that the commitments are binding to these values.

We use the Consistency Check performed in the second half of Fig. 4 to define a set $E \subseteq \{ 1, \ldots , n \}$. We call this the erasure set. This name will make sense later, but for now think of E as the set of indices for which the corrupted sender $\breve{P_s}$ after the consistency checks knows the choice bits $b_i$ for $i \in E$ and for which the bits $b_i$ for $i \not \in E$ are still uniform in the view of $\breve{P_s}$.

Define the column vectors $\varvec{s}_j^0$ and $\varvec{s}_j^1$ as in the protocol. This is possible as the seeds from $\mathcal {F} _{\textsf {ROT}}$ are well defined. Following the protocol, and adding a few more definitions, define

$$\begin{aligned} \varvec{r}_j^0 =&\pi _k(\varvec{s}_j^0) \ , \ \varvec{r}_j^1 = \pi _k(\varvec{s}_j^1)\ , \ \varvec{r}_j = \varvec{r}_j^0 + \varvec{r}_j^1\ ,\ \varvec{u}_j^0 = \pi _{k+1,n}(\varvec{s}_j^0)\ , \ \varvec{u}_j^1 = \pi _{k+1,n}(\varvec{s}_j^1)\ ,\\ \varvec{u}_j&= \varvec{u}_j^0 + \varvec{u}_j^1\ , \ \varvec{t}_j = \mathcal {C} (\varvec{r}_j)\ , \ \varvec{c}_j = \pi _{k+1,{n}}(\varvec{t}_j)\ , \ \varvec{c}_j^0 = \varvec{u}_j^0\ ,\ \varvec{c}_j^1 = \varvec{c}_j - \varvec{c}_j^0\ ,\\ \varvec{d}_j^0 =&\varvec{u}_j^0\ , \ \varvec{d}_j^1 = \varvec{u}_j^1 + \bar{\varvec{c}}_j\ ,\ \varvec{d}_j = \varvec{d}_j^0 + \varvec{d}_j^1 = \varvec{u}_j + \bar{\varvec{c}}_j\ ,\ \varvec{w}_j^0 = \varvec{r}_j^0 \Vert \varvec{d}_j^0\ ,\ \varvec{w}_j^1 = \varvec{r}_j^1 \Vert \varvec{d}_j^1. \end{aligned}$$

Notice that if $P_s$ is honest, then $\bar{\varvec{c}}_j = \varvec{c}_j - \varvec{u}_j$ and therefore $\varvec{d}_j = \varvec{d}_j^0 + \varvec{d}_j^1 = \varvec{u}_j^0 + \varvec{u}_j^1 + \bar{\varvec{c}}_j = \varvec{c}_j$. Hence $\varvec{d}_j^0$ and $\varvec{d}_j^1$ are the two shares of the non-systematic part $\varvec{c}_j$ the same way that $\varvec{r}_j^0$ and $\varvec{r}_j^1$ are the two shares of the systematic part $\varvec{r}_j$. If the sender was honest we would in particular have that $\varvec{w}_j^0 + \varvec{w}_j^1 = \varvec{r}_j \Vert \varvec{d}_j = \varvec{r}_j \Vert \varvec{c}_j = \mathcal {C} (\varvec{r}_j)$, i.e., $\varvec{w}_j^0$ and $\varvec{w}_j^1$ would be the two shares of the whole codeword.

We can define the values that an honest $P_s$ should send as

$$\begin{aligned} {\tilde{\varvec{r}}}^0 = \varvec{r}^0_{\mathcal {T} +\gamma +1} + \sum _j x_j \varvec{r}_j^0\ , \ {\tilde{\varvec{r}}}^1 = \varvec{r}^1_{\mathcal {T} +\gamma +1} + \sum _j x_j \varvec{r}_j^1\ , \ {\tilde{\varvec{c}}}^0 = \varvec{c}^0_{\mathcal {T} +\gamma +1} + \sum _j x_j \varvec{c}_j^0\ . \end{aligned}$$

These values can be used to define values

$$\begin{aligned} \tilde{\varvec{r}}&= \tilde{\varvec{r}}^0 + \tilde{\varvec{r}}^1\ , \ \tilde{\varvec{t}} = \mathcal {C} ({\tilde{\varvec{r}}})\ ,\ \tilde{\varvec{c}} = \pi _{k+1,n}({\tilde{\varvec{t}}})\ ,\\ \tilde{\varvec{c}}^1&= \tilde{\varvec{c}} - \tilde{\varvec{c}}^0\ ,\ \tilde{\varvec{w}}^0 = \tilde{\varvec{r}}^0 \Vert \tilde{\varvec{c}}^0 \ , \ \tilde{\varvec{w}}^1 = \tilde{\varvec{r}}^1 \Vert \tilde{\varvec{c}}^1\ . \end{aligned}$$

We use $(\breve{\varvec{r}}^0, \breve{\varvec{r}}^1, \breve{\varvec{c}}^0)$ to denote the values actually sent by $\breve{P_s}$ and we let the following denote the values computed by $P_r$ (plus some extra definitions).

$$\begin{aligned} \breve{\varvec{r}}&= \breve{\varvec{r}}^0 + \breve{\varvec{r}}^1\ , \ \breve{\varvec{t}} = \mathcal {C} (\breve{\varvec{r}})\ , \ \breve{\varvec{c}} = \pi _{k+1,n}(\breve{\varvec{t}})\ , \ \\ \breve{\varvec{c}}^1 = \breve{\varvec{c}} -&\breve{\varvec{c}}^0 \ , \ \breve{\varvec{w}}^0 = \breve{\varvec{r}}^0 \Vert \breve{\varvec{c}}^0 \ , \ \breve{\varvec{w}}^1 = \breve{\varvec{r}}^1 \Vert \breve{\varvec{c}}^1\ , \ \breve{\varvec{w}} = \breve{\varvec{w}}^0 + \breve{\varvec{w}}^1\ . \end{aligned}$$

The simulator computes

$$\begin{aligned} \tilde{\varvec{w}} = \varvec{w}_{\mathcal {T} +\gamma +1} + \sum _j x_j \varvec{w}_{\mathcal {T} +j} \end{aligned}$$

(3)

as $P_r$ in the protocol. For later use, define $\tilde{\varvec{w}}^0 = \varvec{w}^0_{\mathcal {T} +\gamma +1} + \sum _j x_j \varvec{w}^0_{\mathcal {T} +j}$ and $\tilde{\varvec{w}}^1 = \varvec{w}^1_{\mathcal {T} +\gamma +1} + \sum _j x_j \varvec{w}^1_{\mathcal {T} +j}$.

The check performed by $P_r$ is then simply to check for $u= 1, \ldots , n$ that

$$\begin{aligned} \breve{\varvec{w}}^{b_u}[u] = \tilde{\varvec{w}}[u]\ . \end{aligned}$$

(4)

Notice that in the protocol we have that $\varvec{w}_j = \varvec{b} * (\varvec{w}_j^1 - \varvec{w}_j^0) + \varvec{w}_j^0$, where $*$ denotes the Schur product also known as the positionwise product of vectors. To see this notice that $(\varvec{b} * (\varvec{w}_j^1 - \varvec{w}_j^0) + \varvec{w}_j^0)[i] = b_i (\varvec{w}_j^1[i] - \varvec{w}_j^0[i]) + \varvec{w}_j^0[i] = \varvec{w}_j^{b_i}[i]$. In other words, $\varvec{w}_j[i] = \varvec{w}_j^{b_i}[i]$. It then follows from (3) that $\tilde{\varvec{w}} = \varvec{b} * (\tilde{\varvec{w}}^1 - \tilde{\varvec{w}}^0) + \tilde{\varvec{w}}^0$, from which it follows that $\tilde{\varvec{w}}[u] = \tilde{\varvec{w}}^{b_u}[u]$. From (4) it then follows that $\breve{P_s}$ passes the consistency check if and only if for $u= 1, \ldots , n$ it holds that $\breve{\varvec{w}}^{b_u}[u] = \tilde{\varvec{w}}^{b_u}[u]$. We make some definitions related to this check. We say that a position $u \in [n]$ is silly if $\breve{\varvec{w}}^{0}[u] \ne \tilde{\varvec{w}}^{0}[u]$ and $\breve{\varvec{w}}^{1}[u] \ne \tilde{\varvec{w}}^{1}[u]$. We say that a position $u \in [n]$ is clean if $\breve{\varvec{w}}^{0}[u] = \tilde{\varvec{w}}^{0}[u]$ and $\breve{\varvec{w}}^{1}[u] = \tilde{\varvec{w}}^{1}[u]$. We say that a position $u \in [n]$ is probing if it is not silly or clean. Let E denote the set of probing positions u. Notice that if there is a silly position u, then $\breve{\varvec{w}}^{b_u}[u] \ne \tilde{\varvec{w}}^{b_u}[u]$ so $\breve{P_s}$ gets caught. We can therefore assume without loss of generality that there are no silly positions. For the probing positions $u \in E$, there is by definition a bit $c_u$ such that $\breve{\varvec{w}}^{1-c_u}[u] \ne \tilde{\varvec{w}}^{1-c_u}[u]$ and such that $\breve{\varvec{w}}^{c_u}[u] = \tilde{\varvec{w}}^{c_u}[u]$. This means that $\breve{P_s}$ passes the test only if $c_u = b_u$ for all $u \in E$. Since $\breve{P_s}$ knows $c_u$ it follows that if $\breve{P_s}$ does not get caught, then it can guess $b_u$ for $u \in E$ with probability 1.

Before we proceed to describe the extractor, we are now going to show two facts about E. First we will show that $\vert E \vert < s$, except with probability $2^{-s}$. This follows from the simple observation that each $b_u$ for $u \in E$ is uniformly random and $\breve{P_s}$ passes the consistency test if and only if $c_u = b_u$ for $u \in E$ and the only information that $\breve{P_s}$ has on the bits $b_u$ is via the probing positions. Hence $\breve{P_s}$ passes the consistency test with probability at most $2^{-\vert E \vert }$.

Second, let $\mathcal {C} _{-E}$ be the code obtained from $\mathcal {C}$ by puncturing at the positions $u \in E$, i.e., a codeword of $\mathcal {C} _{-E}$ can be computed as $\varvec{t} = \mathcal {C} (\varvec{r})$ and then outputting $\varvec{t}_{-E}$, i.e., the vector $\varvec{t}$ where we remove the positions $u \in E$. We show that for all $j = \mathcal {T} + 1, \ldots , \mathcal {T} +\gamma$ it holds that $(\varvec{w}_j^0 + \varvec{w}_j^1)_{-E} \in \mathcal {C} _{-E}({\mathbb {F}}^k)$, except with probability $2^{-s}$. To see this, assume for the sake of contradiction that there exists such j where $(\varvec{w}_j^0 + \varvec{w}_j^1)_{-E} \not \in \mathcal {C} _{-E}({\mathbb {F}}^k)$. Then the probability that it does not happen that $(\tilde{\varvec{w}}^0 + \tilde{\varvec{w}}^1)_{-E} \not \in \mathcal {C} _{-E}({\mathbb {F}}^k)$ is at most $\vert {\mathbb {F}}\vert ^{-1}$, as a random linear combination of non-codewords become a codeword with probability at most $\vert {\mathbb {F}}\vert ^{-1}$.² We repeat this test a number $\hat{s}$ of times such that $\vert {\mathbb {F}}\vert ^{-\hat{s}} \le 2^{-s}$. Since the tests succeed independently with probability at most $\vert {\mathbb {F}}\vert ^{-1}$ it follows that $(\tilde{\varvec{w}}^0 + \tilde{\varvec{w}}^1)_{-E} \not \in \mathcal {C} _{-E}({\mathbb {F}}^k)$ except with probability $2^{-s}$. Since by construction $\breve{\varvec{w}}^0 + \breve{\varvec{w}}^1 \in \mathcal {C} ({\mathbb {F}}^k)$, we have that $(\breve{\varvec{w}}^0 + \breve{\varvec{w}}^1)_{-E} \in \mathcal {C} _{-E}({\mathbb {F}}^k)$, so when $(\tilde{\varvec{w}}^0 + \tilde{\varvec{w}}^1)_{-E} \not \in \mathcal {C} _{-E}({\mathbb {F}}^k)$ we either have that $(\tilde{\varvec{w}}^0)_{-E} \ne (\breve{\varvec{w}}^0)_{-E}$ or $(\tilde{\varvec{w}}^1)_{-E} \ne (\breve{\varvec{w}}^1)_{-E}$. Since there are no silly positions, this implies that we have a new probing position $u \not \in E$, a contradiction to the definition of E.

We can now assume without loss of generality that $\vert E \vert < s$ and that $(\varvec{w}_j^0 + \varvec{w}_j^1)_{-E} \in \mathcal {C} _{-E}({\mathbb {F}}^k)$. From $\vert E \vert < s$ and $\mathcal {C}$ having minimal distance ${d} \ge s$ we have that $\mathcal {C} _{-E}$ has minimal distance $\ge 1$. Hence we can from each j and each $(\varvec{w}_j^0 + \varvec{w}^1_j)_{-E} \in \mathcal {C} _{-E}({\mathbb {F}}^k)$ compute $\tilde{\varvec{r}}_j \in {\mathbb {F}}^k$ such that $(\varvec{w}_j^0 + \varvec{w}_j^1)_{-E} = \mathcal {C} _{-E}(\tilde{\varvec{r}}_j)$. These are the values that $\mathcal {S}$ will send to $\mathcal {F} _{\textsf {HCOM}}$.

We then proceed to show that for all $\{ (c, \alpha _c) \}_{c \in C}$ the environment can open to $({\texttt {opened}}, {\texttt {sid}},\{ (c,\alpha _c) \}_{c \in C},\tilde{\varvec{r}})$ for $\tilde{\varvec{r}} = \sum _{c \in C} \alpha _c \tilde{\varvec{r}}_c$ with probability 1. The reason for this is that if $\breve{P_s}$ computes the values in the opening correctly, then clearly $(\breve{\varvec{w}}^{0})_{-E} = (\tilde{\varvec{w}}^{0})_{-E}$ and $(\breve{\varvec{w}}^{1})_{-E} = (\tilde{\varvec{w}}^{1})_{-E}$. Furthermore, for the positions $u \in E$ it can open to any value as it knows $b_u$. It therefore follows that if $\breve{P_s}$ can open to $({\texttt {opened}}, {\texttt {sid}}, \{ (c, \alpha _c) \}_{c \in C}, \varvec{r})$ for $\varvec{r} \ne \sum _{c \in C} \alpha _c \tilde{\varvec{r}}_c$, then it can open $\{ (c, \alpha _c) \}_{c \in C}$ to two different values. Since the code has distance ${d} \ge s$, it is easy to see that after opening some $\{ (c, \alpha _c) \}_{c \in C}$ to two different values, the environment can compute with probability 1 at least s of the choice bits $b_u$, which it can do with probability at most $2^{-s}$, which is negligible.      $\square$

4 Comparison with Recent Schemes

In this section we compare the efficiency of our scheme to the most efficient schemes in the literature realizing UC-secure commitments with security against a static and malicious adversary. In particular, we compare our construction to the schemes of [Lin11, BCPV13, CJS14, CDD+15].

The scheme of [BCPV13] (Fig. 6) is a slightly optimized version of [Lin11] (Protocol 2) which implement a multi-commitment ideal functionality. Along with [CJS14] these schemes support commitments between multiple parties natively, a property not shared with the rest of the protocols in this comparison. We therefore only consider the two party case where a sender commits to a receiver. The schemes of [Lin11, BCPV13] are in the CRS-model and their security relies on the DDH assumption. As the messages to be committed to are encoded as group elements the message size and the level of security are coupled in these schemes. For large messages this is not a big issue as the group size would just increase as well, or one can break the message into smaller blocks and commit to each block. However, for shorter messages, it is not possible to decrease the group size, as this would weaken security. The authors propose instantiating their scheme over an elliptic curve group over a field size of 256-bits so later in our comparison we also consider committing to values of this length. This is optimal for these schemes as the overhead of working with group elements of 256-bits would become more apparent if committing to smaller values.

The scheme of [CJS14] in the global random oracle model can be based on any stand-alone secure trapdoor commitment scheme, but for concreteness we compare the scheme instantiated with the commitment scheme of [Ped92] as also proposed by the authors. As [Ped92] is also based on the DDH assumption we use the same setting and parameters for [CJS14] as for the former two schemes.

We present our detailed comparison in Table 1. The table shows the costs of all the previously mentioned schemes in terms of OTs required, communication, number of rounds and computation. For the schemes of [CDD+15] we have fixed the sharing parameter t to 2 and 3 for the basic and homomorphic version, respectively. To the best of our knowledge this is also the optimal choice in all settings. Also for the scheme of [CJS14] we do not list the queries to the random oracle in the table, but remark that their scheme requires 6 queries per commitment. For our scheme, instead of counting the cost of sending the challenges $(x_1,x_2,\ldots ,x_\gamma ) \in {\mathbb {F}}$, we assume the receiver sends a random seed of size $\kappa$ instead. This is then used as input to a PRG whose output is used to determine the challenges.

Table 1. Comparison of the most efficient UC-secure schemes for committing to $\gamma$ messages of $k$ components. Sizes are in bits. Legend: g is size of a group element, l is size of a scalar in the exponent, h is the output length of the random oracle, f is the size of a finite field element, $\hat{s}$ is the number of consistency checks performed, Exp. denotes the number of modular exponentiations, Enc. denotes the number of encoding procedures of the corresponding codes which have length $\overline{{n}}$ and ${n}$. The schemes of [CDD+15] are presented with the sharing parameter t set to 2 for the basic and 3 for the homomorphic.

Table 2. Concrete efficiency comparison of the most efficient UC-secure schemes for committing to messages of size $k = 256$, $\kappa = 128$, $h = 256$ and ${s} = 40$ where the field is ${\mathbb {F}}_2$ and hence $\hat{s} =40$. In the table $\gamma$ represents the number of commitments the parties perform. These numbers include the cost of performing the initial OTs, both in terms of communication and computation.

To give a flavor of the actual numbers we compute Table 1 for specific parameters in Table 2. We fix the field to ${\mathbb {F}}_2$ and look at computational security $\kappa =128$, statistical security ${s} = 40$ and instantiate the random oracle required by [CJS14] with SHA-256. As the schemes of [Lin11, BCPV13, CJS14] rely on the hardness of the DDH assumption, a 256-bit EC group is assumed sufficient for 128-bit security [SRG+14]. As already mentioned we look at message length $k =256$ as this is well suited for these schemes.³ The best code we could find for the schemes of [CDD+15] in this setting has parameters [631, 256, 81] and is a shortened BCH code. For our scheme, the best code we have identified for the above parameters is a [419, 256, 40] expurgated BCH code [SS06]. Also, we recall the experiments performed in [CDD+15] showing that exponentiations in a EC-DDH group of the above size require roughly 500 times more computation time compared to encoding using a BCH code for parameters of the above type.⁴ In their brief comparison with [HMQ04], another commitment scheme in the random oracle model, the experiments showed that one of the above BCH encodings is roughly 1.6 times faster than 4 SHA-256 invocations, which is the number of random oracle queries required by [HMQ04]. This therefore suggests that one BCH encoding is also faster than the 6 random oracle queries required by [CJS14] if indeed instantiated with SHA-256.

To give as meaningful comparisons as possible we also instantiate the initial OTs and include the cost of these in Table 2. As the homomorphic version of [CDD+15] require 2-out-of-3 OTs in the setup phase, using techniques described in [LOP11, LP11], we have calculated that these require communicating 26 group elements and 44 exponentiations per invocation. The standard 1-out-of-2 OTs we instantiate with [PVW08] which require communicating 6 group elements and computing 11 exponentiations per invocation.

In Table 2 we do not take into consideration OT extension techniques [Bea96, IKNP03, Nie07, NNOB12, Lar15, ALSZ15, KOS15], as we do so few OTs that even the most efficient of these schemes might not improve the efficiency in practice. We note however that if in a setting where OT extension is already used, this would have a very positive impact on our scheme as the OTs in the setup phase would be much less costly. On a technical note some of the ideas used in this work are very related to the OT extension techniques introduced in [IKNP03] (and used in all follow-up work that make black-box use of a PRG). However an important and interesting difference is that in our work we do not “swap” the roles of the sender and receiver for the initial OTs as otherwise the case for current OT extension protocols. This observation means that the related work of [GIKW14], which makes use of OT extension, would look inherently different from our protocol, if instantiated with one of the OT extension protocols that follow the [IKNP03] blueprint.

As can be seen in Table 2, our scheme improves as the number of committed values $\gamma$ grows. In particular we see that at around 304 commitments, for the above message sizes and security parameters, our scheme outperforms all previous schemes in total communication, while at the same time offering additive homomorphism.

A Protocol Extension

As the scheme presented in Sect. 2 only implements commitments to random values we here describe an efficient extension to chosen message commitments. Our extension $\Pi _{\textsf {EHCOM}}$ is phrased in the $\mathcal {F} _{\textsf {HCOM}}$-hybrid model and it is presented in Fig. 6. The techniques presented therein are folklore and are known to work for any UC-secure commitment scheme, but we include them as a protocol extension for completeness. The Chosen-Commit step shows how one can turn a commitment of a random value into a commitment of a chosen value. This is done by simply using the committed random value as a one-time pad on the chosen value and sending this to $P_r$. The Extended-Open step describes how to open to linear combinations of either random commitments, chosen commitments or both. It works by using $\mathcal {F} _{\textsf {HCOM}}$ to open to the random commitments and the commitments used to one-time pad the chosen commitments. Together with the previously sent one-time pad the receiver can then learn the designated linear combination.

Fig. 6.

Protocol $\Pi _{\textsf {EHCOM}}$ in the $\mathcal {F} _{\textsf {HCOM}}$-hybrid model.

Finally we present a Batch-Open step that achieves very close to optimal amortized communication complexity for opening to a set of messages. The technique is similar to the consistency check of $\Pi _{\textsf {HCOM}}$. When required to open to a set of messages, the sender $P_s$ will start by sending the messages directly to the receiver $P_r$. Next, the receiver challenges the sender to open to a random linear combination of all the received messages. When receiving the opening from $\mathcal {F} _{\textsf {HCOM}}$, $P_r$ verifies that it is consistent with the previously received messages and if this is the case it accepts these. For the exact same reasons as covered in the proof of Theorem 1 it follows that this approach of opening values is secure. For clarity and ease of presentation the description of batch-opening does not take into account opening to linear combinations of random and chosen commitments. However the procedure can easily be extended to this setting using the same approach as in Extended-Open.

In terms of efficiency, to open N commitments with message-size l, the sender needs to send lN field elements along with the verification overhead $\hat{s} \hat{O}+\kappa$ where $\hat{O}$ is the cost of opening to a commitment using $\mathcal {F} _{\textsf {HCOM}}$. Therefore if the functionality is instantiated with the scheme $\Pi _{\textsf {HCOM}}$, the total communication for batch-opening is $\hat{s} (k + {n})f+\kappa + k N f$ bits where $k$ is the length of the message, ${n}$ is the length of the code used, f is the size of a field element and $\hat{s}$ is the number of consistency checks needed.

We now elaborate on the applicability of batch-opening for committing to large messages as mentioned in Sect. 2.3. Recall that there we split the large message m of size M into N blocks of size l and the idea is to instantiate $\Pi _{\textsf {HCOM}}$ with a $[n_s, l, {s} ]$ code and commit to m in blocks of size l. This requires $n_s$ initial OTs to setup and requires sending $(2\hat{s} n_s)f+\kappa + lNf$ bits to commit to all blocks. For a fixed ${s}$ this has rate close to 1 for large enough l. In the opening phase we can then use the above batch-opening technique to open to all the blocks of the original message, and thus achieve a rate of in the opening phase as well.

In [GIKW14] the authors present an example of committing to strings of length $2^{30}$ with statistical security ${s} = 30$ achieving rate $1.046^{-1} \approx 0.95$ in both the commit and open phase. To achieve these number the field size is required to be very large as well. The authors propose techniques to reduce the field size, however at the cost of reducing the rate. We will instantiate the approach described above using a binary BCH code over the field ${\mathbb {F}}_2$ and recall that these have parameters $[n-1, n-\lceil \frac{{d}-1}{2}\rceil \log (n+1),\ge {d} ]$. Using a block length of $2^{13}$ and ${s} =30$ therefore gives us a code with parameters [8191, 7996, 30]. Thus we split the message into blocks. In the commitment phase we therefore achieve rate . Using the batch-opening technique the rate in the opening phase is even higher than in the commit phase, as this does not require any “blinding” values. In the above calculations we do not take into account the 8191 initial OTs required to setup our scheme. However using the OT-extension techniques of [KOS15], each OT for $\kappa$-bit strings can be run using only $\kappa$ initial “seed” OTs and each extended OT then requires only $\kappa$ bits of communication. Instantiating the seed OTs with the protocol of [PVW08] for $\kappa = 128$ results in $6\cdot 256\cdot 128 + 8191 \cdot 128 = 1,245,056$ extra bits of communication which lowers the rate to 0.974.

Finally, based on local experiments with BCH codes with the above parameters, we observe that the running time of an encoding operation using the above larger parameters is roughly 2.5 times slower than an encoding using a BCH code with parameters [796, 256, 121]. This suggests that the above approach remains practical for implementations as well.