Gaussian Process Regression (GPR)

Last Updated : 03 Jun, 2024
Comments
Improve
Suggest changes
Like Article
Like
Save
Share
Report
News Follow

Regression and probabilistic classification issues can be resolved using the Gaussian process (GP), a supervised learning technique. Since each Gaussian process can be thought of as an infinite-dimensional generalization of multivariate Gaussian distributions, the term “Gaussian” appears in the name. We will discuss Gaussian processes for regression in this post, which is also referred to as Gaussian process regression (GPR). Numerous real-world issues in the fields of materials science, chemistry, physics, and biology have been resolved with the use of GPR.

Table of Content

Gaussian Process Regression (GPR)

Gaussian Process Regression (GPR) is a powerful and flexible non-parametric regression technique used in machine learning and statistics. It is particularly useful when dealing with problems involving continuous data, where the relationship between input variables and output is not explicitly known or can be complex. GPR is a Bayesian approach that can model certainty in predictions, making it a valuable tool for various applications, including optimization, time series forecasting, and more. GPR is based on the concept of a Gaussian process, which is a collection of random variables, any finite number of which have a joint Gaussian distribution. A Gaussian process can be thought of as a distribution of functions.

Key Concepts of Gaussian Process Regression (GPR)

Gaussain Process

A non-parametric, probabilistic model called a Gaussian Process (GP) is utilized in statistics and machine learning for regression, classification, and uncertainty quantification. It depicts a group of random variables, each of which has a joint Gaussian distribution and can have a finite number. GPs are a versatile and effective technique for modeling intricate relationships in data and producing forecasts with related uncertainty.

Characteristics of Gaussian Processes:

  • Non-Parametric Nature: GPs can adjust to the complexity of the data because they do not rely on a set number of model parameters
  • Probabilistic Predictions: Predictions from GPs can be quantified because they deliver predictions as probability distributions.
  • Interpolation and Smoothing: GPs are useful for noisy or irregularly sampled data because they are good at smoothing noisy data and interpolating between data points.
  • Marginalization of Hyperparameters: By eliminating the requirement for explicit hyperparameter tweaking, they marginalize over hyperparameters, making the model simpler.

Mean Function

The predicted value of the function being modeled at each input point is represented by the mean function in Gaussian Processes (GPs). It functions as a foundational presumption regarding the underlying data structure. The mean function is frequently set to zero by default not necessarily and can be modified based on data properties or domain expertise. By influencing the central tendency of forecasts, it aids general practitioners in identifying patterns or trends in the data. GPs provide probabilistic predictions that contain uncertainty as well as point estimates by including the mean function

Covariance (Kernel) Function

The covariance function, also referred to as the kernel function, measures how similar the input data points are to one another in Gaussian Processes (GPs). It is essential in characterizing the behavior of the GP model, affecting the selection of functions from the previous distribution. The covariance function measures pairwise similarities to ascertain the correlation between function values. GPs can adjust to a broad range of data patterns, from smooth trends to complex structures, because different kernel functions capture different kinds of correlations. The model’s performance can be greatly impacted by the kernel selection.

Prior Distributions

The prior distribution, in Gaussian Processes (GPs), is our understanding of functions prior to the observation of any data. Usually, it is described by a covariance (kernel) function and a mean function. Whereas the covariance function describes the similarity or correlation between function values at various input points, the mean function encodes our previous expectations. This is used beforehand by GPs to create a distribution over functions. In GPs, priors can be selected to represent data uncertainty, integrate domain knowledge, or indicate smoothness.

Posterior Distributions

Gaussian Processes’ posterior distribution shows our revised assumptions about functions following data observation. It puts together the likelihood of the data given the function and the previous distribution. The posterior in GP regression offers a distribution over functions that most closely match the observed data. By allowing for probabilistic predictions and the quantification of uncertainty, the posterior distribution reflects the trade-off between the prior beliefs stored in the prior distribution and the information supplied by the data.

Mathematical Concept of Gaussian Process Regression (GPR)

For regression tasks, a non-parametric, probabilistic machine learning model called Gaussian Process (GP) regression is employed. When modeling intricate and ambiguous interactions between input and output variables, it’s a potent tool. A multivariate Gaussian distribution is assumed to produce the data points in GP regression, and the objective is to infer this distribution.

The GP regression model has the following mathematical expression. Let’s assume x1 , x2 ,…..,xn are the input data points , where x belong to real numbers(-2,-1,0,1…), (xi [Tex]\epsilon [/Tex] R)

Let’s assume y1 , y2 ,……., yn are the output values, where yi belongs to real number (yi [Tex]\epsilon [/Tex] R)

The GP regression model makes the assumption that a Gaussian process with a mean function ([Tex]\mu [/Tex]) and covariance function (k) provides the function f that connects the inputs to the outputs.

Then, at a set of test locations x*, the distribution of f is given by:

[Tex]f(x^*) ∼ N(\mu(x^*), k(x^*, x^*)) [/Tex]

Typically, kernel functions are used to define the mean function and covariance function. As an illustration, the squared exponential kernel that is frequently employed is described as:

[Tex]k(x_{i},x_{j}) = \sigma^2 exp(-\frac{||x_{i} – x_{j}||^2}{2l^2}) [/Tex]

Where,

  • [Tex]k(x_{i}, x_{j}) [/Tex] = The kernel function is represented by this, and it calculates the correlation or similarity between two input data points, xi and xj .
  • [Tex]\sigma^2 [/Tex] = The kernel’s variance parameter is this. It establishes the kernel function’s scale or vertical spread. It regulates how strongly the data points are correlated. A higher [Tex]\sigma^2 [/Tex] yields a kernel function with greater variance.
  • exp: The exponential function is responsible for raising e to the argument’s power.
  • [Tex]||x_{i} – x_{j}||^2 [/Tex]: The difference between the input data points, xi and xj, is the squared Euclidean distance. The geometric separation between the points in the feature space is measured.
  • l2: This is a representation of the kernel’s length scale or characteristic length. It regulates the rate at which the kernel function deteriorates as data points are farther apart. A lower l causes the kernel to degrade faster.

The GP regression model applies Bayesian inference to determine the distribution of f that is most likely to have produced the data given a set of training data (x, y). In order to do this, the posterior distribution of f given the data must be calculated, which is defined as follows:

[Tex]p(f|x,y) =\frac {p(y|x,f)p(f)} {p(y|x)} [/Tex]

where the marginal probability of the data is p(y|x), the prior distribution of f is p(f), and the likelihood of the data given the function f is (y|x,f).

After learning the posterior distribution of f, the model computes the posterior predictive distribution to make predictions at additional test points x*. It can be defined as follows:

[Tex]p(f^*|x^*, y,x) = \int p(f^*|x^*, f), p(f|y,x)df [/Tex]

Where,

  • [Tex]p(f^*|x*, y, x) [/Tex] = This shows, given the training data y and x, the conditional probability of the predicted function values f* at a fresh input point x* To put it another way, it’s the probability distribution over all potential function values at the new input site x*, conditioned on the observed data y and their matching input locations x.
  • [Tex]\int p(f^*|x^*, f)p(f|y,x)df [/Tex] = An integral is employed in this section of the equation to determine the conditional probability. The integral encompasses all potential values of the function f.
  • [Tex]p(f^*|x^*, f) [/Tex] = This is the conditional probability distribution of the expected function values f* at x*, given the function values f at some intermediate locations.
  • [Tex]p(f|y,x) [/Tex] = Given the observed data (y) and their input locations (x), this is the conditional probability distribution of the function values (f).

For tasks like uncertainty-aware decision making and active learning, this distribution offers a measure of the prediction’s uncertainty, which can be helpful.

Steps in Gaussian Process Regression

  • Data Collection: Gather the input-output data pairs for your regression problem.
  • Choose a Kernel Function: Select an appropriate covariance function (kernel) that suits your problem. The choice of kernel influences the shape of the functions that GPR can model.
  • Parameter Optimization: Estimate the hyperparameters of the kernel function by maximizing the likelihood of the data. This can be done using optimization techniques like gradient descent.
  • Prediction: Given a new input, use the trained GPR model to make predictions. GPR provides both the predicted mean and the associated uncertainty (variance).

Implementation of Gaussian Process Regression (GPR)

Python

import numpy as np import matplotlib.pyplot as plt from sklearn.gaussian_process import GaussianProcessRegressor from sklearn.gaussian_process.kernels import RBF from sklearn.model_selection import train_test_split # Generate sample data np.random.seed(0) X = np.sort(5 * np.random.rand(80, 1), axis=0) y = np.sin(X).ravel() # Add noise to the data y += 0.1 * np.random.randn(80) # Define the kernel (RBF kernel) kernel = 1.0 * RBF(length_scale=1.0) # Create a Gaussian Process Regressor with the defined kernel gp = GaussianProcessRegressor(kernel=kernel, n_restarts_optimizer=10) # Split the data into training and testing sets X_train, X_test, y_train, y_test = train_test_split( X, y, test_size=0.5, random_state=0) # Fit the Gaussian Process model to the training data gp.fit(X_train, y_train) # Make predictions on the test data y_pred, sigma = gp.predict(X_test, return_std=True) # Visualize the results x = np.linspace(0, 5, 1000)[:, np.newaxis] y_mean, y_cov = gp.predict(x, return_cov=True) plt.figure(figsize=(10, 5)) plt.scatter(X_train, y_train, c='r', label='Training Data') plt.plot(x, y_mean, 'k', lw=2, zorder=9, label='Predicted Mean') plt.fill_between(x[:, 0], y_mean - 1.96 * np.sqrt(np.diag(y_cov)), y_mean + 1.96 * np.sqrt(np.diag(y_cov)), alpha=0.2, color='k', label='95% Confidence Interval') plt.xlabel('X') plt.ylabel('y') plt.legend() plt.show()

Output:

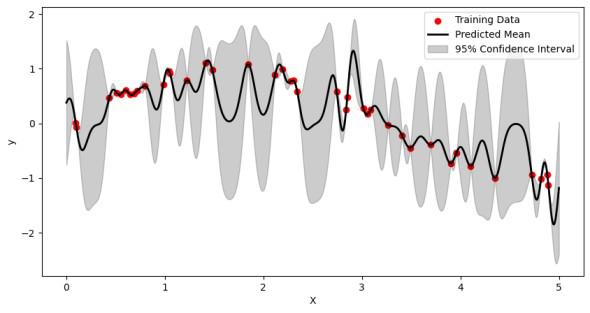
gpr-Geeksforgeeks

In this code, first generate some sample data points with added noise then define an RBF kernel and create a Gaussian Process Regressor with it. The model is trained on the training data and used to make predictions on the test data. Finally, the results are visualized with a plot showing the training data, the predicted mean, and the 95% confidence interval.

Implementation of Gaussian Process in Python

Scikit Learn

Python

import matplotlib.pyplot as plt import numpy as np from scipy import linalg from sklearn.gaussian_process import kernels,GaussianProcessRegressor ## check version import sys import sklearn print(sys.version) !python --version print("numpy:", np.__version__) print("sklearn:",sklearn.__version__)

The necessary libraries for Gaussian Process Regression (GPR) in Python are imported by this code; these are SciPy for linear algebra functions, NumPy for numerical operations, and Matplotlib for data visualization. To make sure it is compatible with the necessary packages, it additionally verifies the version of Python and prints it, along with the versions of NumPy and scikit-learn (sklearn).

Kernel Selection

Python

np.random.seed(0) n=50 kernel_ =[kernels.RBF (), kernels.RationalQuadratic(), kernels.ExpSineSquared(periodicity=10.0), kernels.DotProduct(sigma_0=1.0)**2, kernels.Matern() ] print(kernel_, '\n')

Output:

[RBF(length_scale=1),
RationalQuadratic(alpha=1, length_scale=1),
ExpSineSquared(length_scale=1, periodicity=10),
DotProduct(sigma_0=1) ** 2,
Matern(length_scale=1, nu=1.5)]

The code specifies the number of test sites (n) and initializes a random seed. In order to display the chosen kernels, it generates a list of several kernel functions and prints the list.

Kernel Comparison and Visualization

Python

for kernel in kernel_: # Gaussian process gp = GaussianProcessRegressor(kernel=kernel) # Prior x_test = np.linspace(-5, 5, n).reshape(-1, 1) mu_prior, sd_prior = gp.predict(x_test, return_std=True) samples_prior = gp.sample_y(x_test, 3) # plot plt.figure(figsize=(10, 3)) plt.subplot(1, 2, 1) plt.plot(x_test, mu_prior) plt.fill_between(x_test.ravel(), mu_prior - sd_prior, mu_prior + sd_prior, color='aliceblue') plt.plot(x_test, samples_prior, '--') plt.title('Prior') # Fit x_train = np.array([-4, -3, -2, -1, 1]).reshape(-1, 1) y_train = np.sin(x_train) gp.fit(x_train, y_train) # posterior mu_post, sd_post = gp.predict(x_test, return_std=True) mu_post = mu_post.reshape(-1) samples_post = np.squeeze(gp.sample_y(x_test, 3)) # plot plt.subplot(1, 2, 2) plt.plot(x_test, mu_post) plt.fill_between(x_test.ravel(), mu_post - sd_post, mu_post + sd_post, color='aliceblue') plt.plot(x_test, samples_post, '--') plt.scatter(x_train, y_train, c='blue', s=50) plt.title('Posterior') plt.show() print("gp.kernel_", gp.kernel_) print("gp.log_marginal_likelihood:", gp.log_marginal_likelihood(gp.kernel_.theta)) print('-'*50, '\n\n')

Output:

RBF

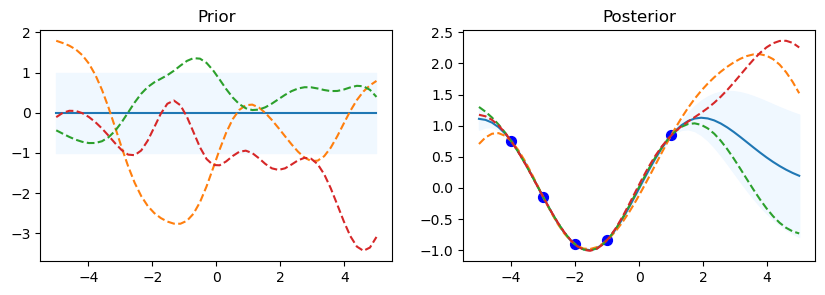
graph-1-Geeksforgeeks

gp.kernel_ RBF(length_scale=1.93)
gp.log_marginal_likelihood: -3.444937833462133
---------------------------------------------------

Rational Quadratic

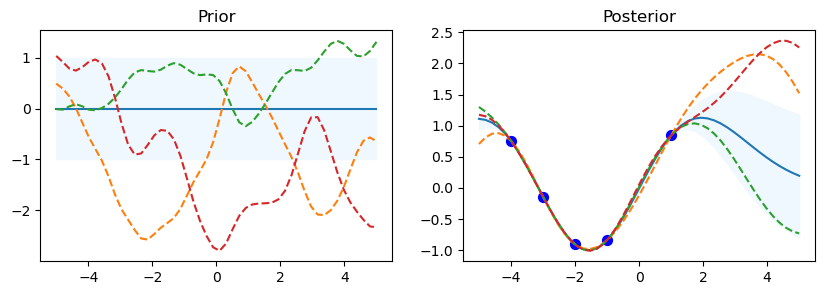
graph-2-Geeksforgeeks

gp.kernel_ RationalQuadratic(alpha=1e+05, length_scale=1.93)
gp.log_marginal_likelihood: -3.4449718909150966
--------------------------------------------------

ExpSineSquared

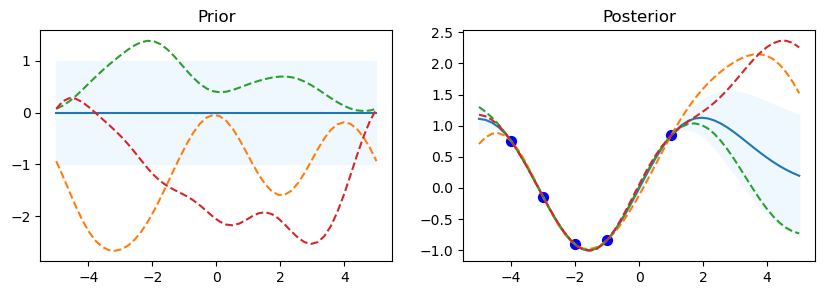
graph-3-Geeksforgeeks

gp.kernel_ ExpSineSquared(length_scale=0.000524, periodicity=2.31e+04)
gp.log_marginal_likelihood: -3.4449381454930217
--------------------------------------------------

Dot Product

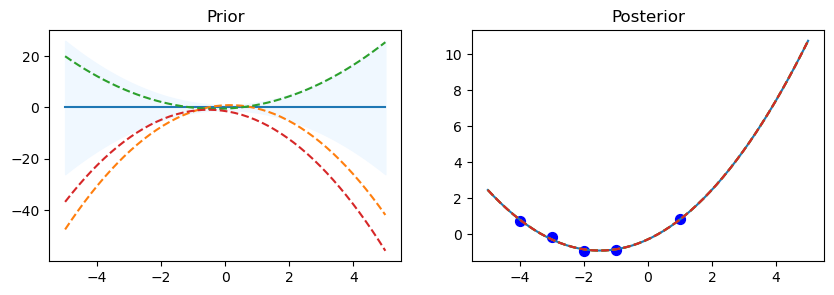
graph-4-Geeksforgeeks

gp.kernel_ DotProduct(sigma_0=0.998) ** 2
gp.log_marginal_likelihood: -150204291.56018084
--------------------------------------------------

Matern

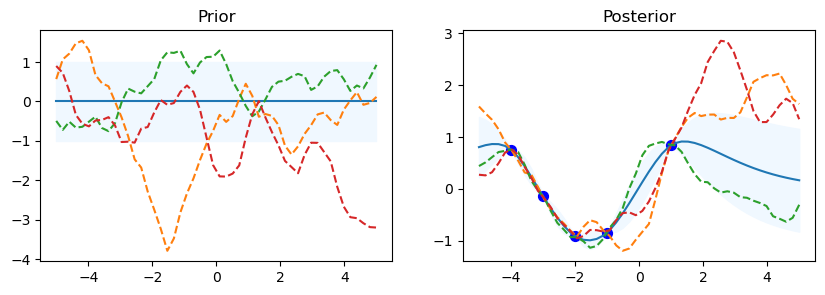
graph-5-Geeksforgeeks

gp.kernel_ Matern(length_scale=1.99, nu=1.5)
gp.log_marginal_likelihood: -5.131637070524745
--------------------------------------------------

The code starts by looping over the various kernel functions listed in the kernel_ list. A Gaussian Process Regressor (gp) is made using the particular kernel for every kernel. For the Gaussian Process, this establishes the covariance structure. In order to assess the previous distribution, a set of test input points called x_test is established, with values ranging from -5 to 5. This set of points is transformed into a column vector.

Using the gp.predict method, the prior distribution’s mean (mu_prior) and standard deviation (sd_prior) are determined at each test point. Standard deviation values are requested using the return_std=True option. gp.sample_y(x_test, 3) is used to get three function samples from the previous distribution.

The first subplot shows the previous distribution’s mean, with the standard deviation represented by a shaded area. The samples are superimposed as dashed lines, while the mean is displayed as a solid line. There is a subplot called “Prior.” There is a defined set of training data points (x_train) and goal values (y_train) that go with them. The Gaussian Process model is fitted using these points (gp.fit(x_train, y_train)). Five data points with corresponding sine values make up the training data in this code.

Following the training data fitting phase, the procedure computes the posterior distribution’s mean (mu_post) and standard deviation (sd_post) for the same test points (x_test). gp.sample_y(x_test, 3) is also used to produce function samples from the posterior distribution. The second subplot overlays the sampled functions as dotted lines and shows the mean of the posterior distribution, shaded with the standard deviation. Plotted in blue are the training data points. The subplot has the name “Posterior.”

To see the previous and posterior plots for the current kernel and gain a visual understanding of the behavior of the model, call Matplotlib’s plt.show() function.

The code shows details about the current kernel, such as gp.kernel_, which indicates the current kernel being used, and gp.log_marginal_likelihood(gp.kernel_.theta), which gives the log marginal likelihood of the model using the current kernel, after each set of prior and posterior plots.

Advantages of Gaussian Process Regression (GPR)

Gaussian Process Regression (GPR) has a number of benefits in a range of applications:

  • GPR provides a probabilistic framework for regression, which means it not only gives point estimates but also provides uncertainty estimates for predictions.
  • It is highly flexible and can capture complex relationships in the data.
  • GPR can be adapted to various applications, including time series forecasting, optimization, and Bayesian optimization.

Challenges of Gaussian Process Regression (GPR)

  • GPR can be computationally expensive when dealing with large datasets, as the inversion of a covariance matrix is required.
  • The choice of the kernel function and its hyperparameters can significantly impact the model’s performance.

Good Examples of GPR Applications

  • Stock Price Prediction: GPR can be used to model and predict stock prices, taking into account the volatility and uncertainty in financial markets.
  • Computer Experiments: GPR is useful in optimizing complex simulations by modeling the input-output relationships and identifying the most influential parameters.
  • Anomaly Detection: GPR can be applied to anomaly detection, where it identifies unusual patterns in time series data by capturing normal data distributions.

Conclusion

In conclusion, Gaussian Process Regression is a valuable tool for data analysis and prediction in situations where understanding the uncertainty in predictions is essential. By leveraging probabilistic modeling and kernel functions, GPR can provide accurate and interpretable results. However, it’s crucial to consider the computational cost and the need for expert input when implementing GPR in practice.



P
phadatareisha
News
Improve
Next Article
Gaussian Process Regression (GPR) on Mauna Loa CO2 data

Similar Reads

Gaussian Process Regression (GPR) with Noise-Level Estimation
GPR is a machine learning technique capable of modeling complex nonlinear relationships between input and output variables. GPR can also estimate the level of noise in data, which is useful when dealing with noisy or uncertain observations. In this response, I will explain some fundamental GPR concepts and demonstrate how to use Scikit Learn to per
14 min read
Gaussian Process Regression (GPR) on Mauna Loa CO2 data
In article explores the application of Gaussian Process Regression (GPR) on the Mauna Loa CO2 dataset using Scikit-Learn. What is Gaussian Process Regression (GPR)? Gaussian Process Regression is the process of making predictions about an unknown function and dealing with regression problems with the help of statistical methods. GPR allows for flex
11 min read
Quick Start to Gaussian Process Regression
Gaussian Processes, often abbreviated as GPs, are powerful and flexible machine-learning techniques primarily used for regression and probabilistic modelling. They excel at modelling intricate relationships between input variables and their corresponding output values. GPs offer methods to estimate both the mean and uncertainty (variance) of predic
6 min read
Prior and Posterior Gaussian Process for Different kernels in Scikit Learn
In this article, we will learn about the Prior and Posterior Gaussian Processes for Different kernels. But first, let's understand what is Prior and Posterior Gaussian Processes are. After that, we will use the sci-kit learn library to see the code implementation for the same in Python. What is the Prior and Posterior Gaussian Process? In Gaussian
6 min read
Gaussian Process Classification (GPC) on the XOR Dataset in Scikit Learn
Gaussian process classification (GPC) is a probabilistic approach to classification that models the conditional distribution of the class labels given the feature values. In GPC, the data is assumed to be generated by a Gaussian process, which is a stochastic process that is characterized by its mean and covariance functions. The mean function in G
4 min read
Probabilistic Predictions with Gaussian Process Classification (GPC) in Scikit Learn
Gaussian Process Classification (GPC) is a probabilistic model for classification tasks. It is based on the idea of using a Gaussian process to model the relationship between the input features and the target labels of a classification problem. GPC makes use of Bayesian inference to make predictions, which means that it can output not only the most
7 min read
Gaussian Process Classification (GPC) on Iris Dataset
A potent machine learning approach that may be used for both regression and classification problems is Gaussian process classification or GPC. It is predicated on the notion of using a probabilistic model that depicts a distribution across functions, known as a Gaussian process. Using this distribution, one may forecast a function's output given a
7 min read
ML | Linear Regression vs Logistic Regression
Linear Regression is a machine learning algorithm based on supervised regression algorithm. Regression models a target prediction value based on independent variables. It is mostly used for finding out the relationship between variables and forecasting. Different regression models differ based on – the kind of relationship between the dependent and
3 min read
The Difference between Linear Regression and Nonlinear Regression Models
areRegression analysis is a fundamental tool in statistical modelling used to understand the relationship between a dependent variable and one or more independent variables. Two primary types of regression models are linear regression and nonlinear regression. This article delves into the key differences between these models, their applications, an
7 min read
How to improve the performance of segmented regression using quantile regression in R?
Segmented regression, also known as piecewise or broken-line regression is a powerful statistical technique used to identify changes in the relationship between a dependent variable and one or more independent variables. Quantile regression, on the other hand, estimates the conditional quantiles of a response variable distribution in the linear mod
8 min read
Gaussian Mixture Model
Suppose there are a set of data points that need to be grouped into several parts or clusters based on their similarity. In Machine Learning, this is known as Clustering. There are several methods available for clustering: K Means ClusteringHierarchical ClusteringGaussian Mixture Models In this article, Gaussian Mixture Model will be discussed. Nor
6 min read
Iso-Probability Lines for Gaussian Processes Classification (GPC) in Scikit Learn
Gaussian Processes (GPs) are a powerful tool for probabilistic modeling and have been widely used in various fields such as machine learning, computer vision, and signal processing. Gaussian Processes Classification is a classification technique based on Gaussian Processes to model the probability of an input belonging to a certain class. In GPC, w
11 min read
Gaussian Naive Bayes
In the vast field of machine learning, classification algorithms play a pivotal role in making sense of data. One such algorithm, Gaussian Naive Bayes, stands out for its simplicity, efficiency, and effectiveness. In this article, we will delve into the principles behind Gaussian Naive Bayes, explore its applications, and understand why it is a pop
6 min read
Gaussian Naive Bayes using Sklearn
In the world of machine learning, Gaussian Naive Bayes is a simple yet powerful algorithm used for classification tasks. It belongs to the Naive Bayes algorithm family, which uses Bayes' Theorem as its foundation. The goal of this post is to explain the Gaussian Naive Bayes classifier and offer a detailed implementation tutorial for Python users ut
8 min read
Gaussian Processes in Machine Learning
In the world of machine learning, Gaussian Processes (GPs) is a powerful, flexible approach to modeling and predicting complex datasets. GPs belong to a class of probabilistic models that are particularly effective in scenarios where the prediction not only involves the most likely outcome but also the uncertainty around it. Imagine you're trying t
9 min read
What is Gaussian mixture model clustering using R
Gaussian mixture model (GMM) clustering is a used technique in unsupervised machine learning that groups data points based on their probability distributions. In R Programming Language versatility lies in its ability to model clusters of shapes and sizes making it applicable to scenarios. The approach assumes that the data consists of a mixture of
8 min read
Gaussian Mixture Models (GMM) Covariances in Scikit Learn
Gaussian Mixture Models (GMMs) are a type of probabilistic model used for clustering and density estimation. They assist in representing data as a combination of different Gaussian distributions, where each distribution is characterized by its mean, covariance, and weight. The Gaussian mixture model probability distribution class allows us to estim
6 min read
Why Use a Gaussian Kernel as a Similarity Metric?
Answer: A Gaussian kernel offers smoothness, flexibility, and non-linearity in capturing complex relationships between data points, making it suitable for various machine-learning tasks such as clustering, classification, and regression.Using a Gaussian kernel as a similarity metric in machine learning has several advantages, which can be explained
3 min read
ML | Variational Bayesian Inference for Gaussian Mixture
Prerequisites: Gaussian Mixture A Gaussian Mixture Model assumes the data to be segregated into clusters in such a way that each data point in a given cluster follows a particular Multi-variate Gaussian distribution and the Multi-Variate Gaussian distributions of each cluster is independent of one another. To cluster data in such a model, the poste
5 min read
Gaussian Discriminant Analysis
Gaussian Discriminant Analysis (GDA) is a supervised learning algorithm used for classification tasks in machine learning. It is a variant of the Linear Discriminant Analysis (LDA) algorithm that relaxes the assumption that the covariance matrices of the different classes are equal. GDA works by assuming that the data in each class follows a Gaussi
7 min read
How to plot the decision boundary for a Gaussian Naive Bayes classifier in R?
Gaussian Naive Bayes (GNB) is a simple yet powerful algorithm often used for classification problems. One of the key ways to understand and interpret the behavior of this classifier is by visualizing the decision boundary. This article provides a step-by-step guide on how to plot the decision boundary for a Gaussian Naive Bayes classifier in R. Int
3 min read
Gaussian Distribution In Machine Learning
The Gaussian distribution, also known as the normal distribution, plays a fundamental role in machine learning. It is a key concept used to model the distribution of real-valued random variables and is essential for understanding various statistical methods and algorithms. Table of Content Gaussian Distribution Gaussian Distribution Curve Gaussian
7 min read
Multiple Linear Regression using R
Prerequisite: Simple Linear-Regression using RLinear Regression: It is the basic and commonly used type for predictive analysis. It is a statistical approach for modeling the relationship between a dependent variable and a given set of independent variables.These are of two types: Simple linear RegressionMultiple Linear Regression Let's Discuss Mul
3 min read
Linear Regression using PyTorch
Linear Regression is a very commonly used statistical method that allows us to determine and study the relationship between two continuous variables. The various properties of linear regression and its Python implementation have been covered in this article previously. Now, we shall find out how to implement this in PyTorch, a very popular deep lea
4 min read
Identifying handwritten digits using Logistic Regression in PyTorch
Logistic Regression is a very commonly used statistical method that allows us to predict a binary output from a set of independent variables. The various properties of logistic regression and its Python implementation have been covered in this article previously. Now, we shall find out how to implement this in PyTorch, a very popular deep learning
6 min read
Mathematical explanation for Linear Regression working
Suppose we are given a dataset: Given is a Work vs Experience dataset of a company and the task is to predict the salary of a employee based on his / her work experience. This article aims to explain how in reality Linear regression mathematically works when we use a pre-defined function to perform prediction task. Let us explore how the stuff work
1 min read
ML | Boston Housing Kaggle Challenge with Linear Regression
Boston Housing Data: This dataset was taken from the StatLib library and is maintained by Carnegie Mellon University. This dataset concerns the housing prices in the housing city of Boston. The dataset provided has 506 instances with 13 features.The Description of the dataset is taken from the below reference as shown in the table follows: Let's ma
3 min read
ML | Normal Equation in Linear Regression
We know the Linear Regression model is a parameterized model which means that the model's behavior and predictions are determined by a set of parameters or coefficients in the model. However, we use different methods for finding these parameters which give the lowest error on our dataset. In this article, we will read one such article which is the
4 min read
Python | Decision Tree Regression using sklearn
Decision Tree is a decision-making tool that uses a flowchart-like tree structure or is a model of decisions and all of their possible results, including outcomes, input costs, and utility.Decision-tree algorithm falls under the category of supervised learning algorithms. It works for both continuous as well as categorical output variables. The bra
4 min read
ML | Locally weighted Linear Regression
Linear Regression is a supervised learning algorithm used for computing linear relationships between input (X) and output (Y). The steps involved in ordinary linear regression are: Training phase: Compute [Tex]\theta [/Tex]to minimize the cost. [Tex]J(\theta) = $\sum_{i=1}^{m} (\theta^Tx^{(i)} - y^{(i)})^2 [/Tex] Predict output: for given query poi
3 min read
Article Tags :
Practice Tags :