Computational Motor Control: Optimal Control for Stochastic Systems (JAIST summer course)
- 1. Computational Motor Control Summer School 05: Optimal control for stochastic systems. Hirokazu Tanaka School of Information Science Japan Institute of Science and Technology
- 2. Optimal control for stochastic systems. In this lecture, we will learn: • Feedforward and feedback control • Trial-by-trial variability • Signal-dependent noise • Dynamic programming • Bellman’s optimality equation • Linear-quadratic-Gaussian (LQG) control • Optimal feedback control (OFC) model • Human psychophysics
- 3. Feedforward and feedback control. Feedforward control as a function of time step: 1k k k x Ax Bu k k ku u Feedback control as a function of state: k k ku u x For a deterministic system, feedforward and feedback control are equivalent. On the other hand, for a stochastic system, feedforward and feedback control are NOT equivalent.
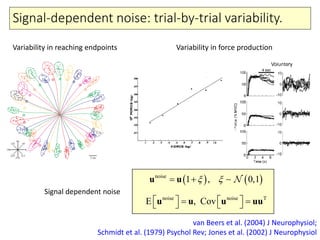
- 4. Signal-dependent noise: trial-by-trial variability. van Beers et al. (2004) J Neurophysiol; Schmidt et al. (1979) Psychol Rev; Jones et al. (2002) J Neurophysiol Variability in reaching endpoints Variability in force production noise 0, 11 , u u noise noise T E , Cov u u u uu Signal dependent noise
- 5. Minimum-variance control predicts smooth trajectory. Harris & Wolpert (1998) Nature 1 1n n n n x Ax Bu 1 1 1 2 2 2 2 1 1 1 0 0 1 1 1 1 1 n n k k n n n n n n n n n n k k x Ax Bu A x ABu Bu A x A Bu 0 1 0 1 E n k n n n k k x A x A Bu T1 T 1 0 T 1 Cov n k n k n k k n k x A Bu u B A
- 6. Minimum-variance control predicts smooth trajectory. Harris & Wolpert (1998) Nature 0 1 1 0 E n n k n k n k f ft t T x A x A Bu x T1 T T 1 11 110 1 Cov f f f f T n k n t t T n k t n t k n k t k x A Bu u B A Minimize the variance of final position (quadratic with respect to u) under constraints (T+1 constraints with respect to u) This problem can be solved with quadratic programming (quadprog command).
- 7. Minimum-variance control predicts smooth trajectory. Harris & Wolpert (1998) Nature Saccade velocity Reaching and drawing
- 8. Minimum-time control predicts Fitts’ law and main sequence. Tanaka et al. (2006) J Neurophysiol Faster, but less accurate 300ms 700ms More precise, but slower 500ms Unique movement time can be determined MT , T 1 Var (t ( ) E ( ) { } ) t tf p f t tf p f f p t f t f f V d dt t t t S t t t μ x x u x minimization of movement time final variance constraint final position constraint
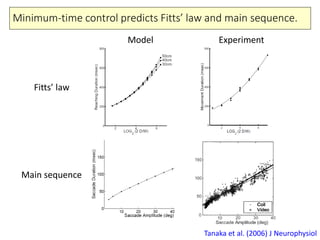
- 9. Minimum-time control predicts Fitts’ law and main sequence. Tanaka et al. (2006) J Neurophysiol Fitts’ law Main sequence Model Experiment
- 10. Optimal control: Bellman’s optimality equation. 1 0 1 1 0 0 1 1 , , , ; 2 2 N T T T N k k k k k N N N k J u u u x x Q x u Ru x Q x 1k k k x Ax Bu Error during movement Control cost Endpoint error Find control signals {u0, u1, …, uN-1} that minimize the cost function. Deterministic (i.e., noiseless) dynamics: Cost function:
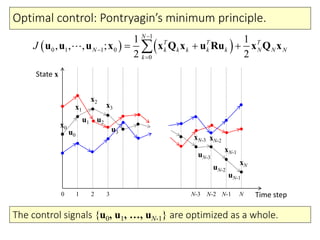
- 11. Optimal control: Pontryagin’s minimum principle. State x Time stepNN-1N-2N-30 1 2 3 u0 u1 u2 u3 uN-3 uN-2 uN-1 x0 x1 x2 x3 xN-3 xN-2 xN-1 xN 1 0 1 1 0 0 1 1 , , , ; 2 2 N T T T N k k k k k N N N k J u u u x x Q x u Ru x Q x The control signals {u0, u1, …, uN-1} are optimized as a whole.
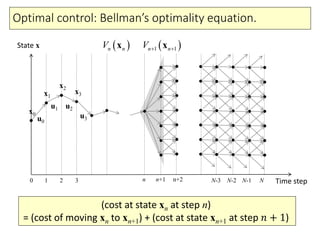
- 12. Optimal control: Bellman’s optimality equation. State x Time stepNN-1N-2N-30 1 2 3 u0 u1 u2 u3 x0 x1 x2 x3 n n+1 n+2 (cost at state xn at step n) = (cost of moving xn to xn+1) + (cost at state xn+1 at step 𝑛 + 1) 1 1n nV x n nV x
- 13. Optimal control: Bellman’s optimality equation. 1 1 1 , , , 1 1 2 2minn n N N T T T n n k k k k k N N N k n V u u u x x Q x u Ru x Q x 1 1 1 1 1 , , , 1 , , 1 1 1 2 2 1 1 1 2 2 2 min min min n N nn N n N T T T n n k k k k k N N N k n N T T T T T n n n n n k k k k k N N N nk V u u u u u u x x Q x u Ru x Q x x Q x u Ru x Q x u Ru x Q x 1 1 1 2minn T T n n n n n n nV u x Q x u Ru x 1 1n nV x 1 1 1 2minn T T n n n n n n n n nV V u x x Q x u Ru x
- 14. Solvable example: Linear-Quadratic-Regulator control. 1 1 1 1 1 1 2 2 1 1 2 2 min min T T T k k k k k k k k k u TT T k k k k k k k k k k u V x x Q x u Ru x S x x Q x u Ru Ax Bu S Ax Bu 1 1 1 1 1 0 2 T T T T T T T k k k k k k k k k k T T k k k k u Ru u B ABu x A S Bu u B S Ax u R B S B u B S Ax 1 1 1 T T k k k k k k u R B S B B S Ax L x Assume that the cost-to-go function has a quadratic form: 1 1 1 1 1 2 T k k k kV x x S x Substituting this into the Bellman equation gives Then, by minimizing with respect to u, A feedback control law is obtained:
- 15. Solvable example: Linear-Quadratic-Regulator control. 1 1 1 T T k k k k k k u R B S B B S Ax L x 11 1 1 1 1 2 2 T T T k k k k k k k k k V x x S x x Q A S BR B A x 11 1 1 T T k k k S Q A S BR B A Substituting the control law into the Bellman equation gives Therefore a backward recursive equation for the matrix S is obtained. 0 S0 L0 1 S1 L1 2 S2 k-1 Sk-1 Lk-1 k Sk Lk k+1 Sk+1 Lk-2 N-1 SN-1 LN-1 N SN LN-2
- 16. Solvable example: Linear-Quadratic-Regulator control. k k k u L x 1 1 1 T T k k k L R B S B B S A 11 1 1 T T k k k S Q A S BR B A N NS Q Backward recursion equation for the matrix S: Feedback control law: where with the terminal condition Therefore, once the matrices {S0, …, SN} and {L0, …, LN-1} are obtained, the optimal feedback control signals {u0, …, uN-1} can be computed.
- 17. Deterministic and stochastic optimal control. 1 0 1 1 0 0 1 1 , , , ; 2 2 N T T T N k k k k k N N N k J u u u x x Q x u Ru x Q x 1 0 1 1 0 , 0 0 1 1 ˆ, , , ; E, 2 2 N T T T N k k k k k N N N k J w v u u u x x Q x u Ru x Q x 1k k k k k x Ax Bu y Cx 1k k k k kk k w v x Ax Bu y Cx Deterministic Optimal Control Stochastic Optimal Control
- 18. Stochastic optimal control combines Kalman filter and feedback control. ˆk k k u L x 1 ˆ ˆ ˆk k k k k k x Ax Bu K y Cx 1 0 1 1 0 , 0 0 1 1 ˆ, , , ; E, 2 2 N T T T N k k k k k N N N k J w v u u u x x Q x u Ru x Q x 1k k k k kk k w v x Ax Bu y Cx Stochastic Optimal Control Optimal state estimation (Kalman Filter) Feedback controller
- 20. Optimal feedback control as a model of motor control. Todorov & Jordan (2002) Nature Neurosci 1 0 1 1 0 , 0 0 1 1 ˆ, , , ; , E 2 2 N T T T N k k k k k N N N k J ω u u u x x Q x u Ru x Q x 1 k k k k k k k k x Ax Bu C y Hx ω u
- 21. Optimal feedback control as a model of motor control. Todorov & Jordan (2002) Nature Neurosci; Todorov (2005) Neural Comput Kalman filter: 1 ˆ ˆ ˆk k k k k k x Ax Bu K y Hx 1T T T T T 1 1 1 1 ˆ T ˆ ˆ 1 ; ˆˆ; k k k k k k k k k T T k k k k k k e x x x e ω e e x e e K A H H A K H A CL L C K H A A BL A BL x Ω x H Feedback control: ˆk k k u L x 1 T T T 1 1 1 1 T 1 TT 1 1 ; ; k N N k k k k k k k k N k k k k k k Q e e e e x x x x x x x L B S B R C S S C B S A S Q A S A BL S S A S BL A K H S A K H S 0
- 22. Infinite-horizon optimal feedback control. Phillis (1985) IEEE Trans Auto Contr; Qian et al. (2013) Neural Comput ,d dd dt d d dt d x Yu G y Cx x Bu x D A F T T T 1 2 0 1 limE E lim t t t J J J dt t x Ux x Qx u Ru Stochastic dynamics with signal- and state-dependent noises: Infinite-horizon cost: . ˆ ,ˆ ˆ ˆd dt d dt x Ax Bu y u x L C x K In infinite-horizon optimal feedback control, the Kalman gain (K) and the feedback gain (L) are time invariant.
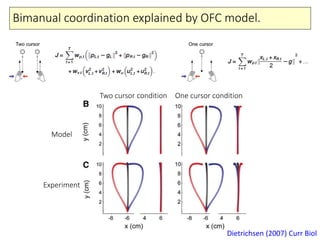
- 23. Bimanual coordination explained by OFC model. Dietrichsen (2007) Curr Biol Two cursor condition One cursor condition Model Experiment
- 24. Motor adaptation as reoptimization. Izawa et al. (2008) J Neurosci Sigmoidal paths Model Experiment Field uncertainty Model Experiment
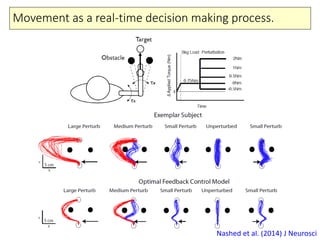
- 25. Movement as a real-time decision making process. Nashed et al. (2014) J Neurosci
- 26. Summary • Feedforward and feedback control differ in stochastic dynamics. • Signal-dependent control noise contributes to trial-by- trial motor variability. • Movement accuracy under signal-dependent noise models human movements. • Optimal feedback control (OFC) integrates state estimation and motor control in a single computational framework. • A number of psychophysical experiments can be explained by the OFC model.
- 27. References • Schmidt, R. A., Zelaznik, H., Hawkins, B., Frank, J. S., & Quinn Jr, J. T. (1979). Motor-output variability: a theory for the accuracy of rapid motor acts. Psychological review, 86(5), 415. • van Beers, R. J., Haggard, P., & Wolpert, D. M. (2004). The role of execution noise in movement variability. Journal of Neurophysiology, 91(2), 1050-1063. • Harris, C. M., & Wolpert, D. M. (1998). Signal-dependent noise determines motor planning. Nature, 394(6695), 780-784. • Tanaka, H., Krakauer, J. W., & Qian, N. (2006). An optimization principle for determining movement duration. Journal of neurophysiology, 95(6), 3875-3886. • Todorov, E., & Jordan, M. I. (2002). Optimal feedback control as a theory of motor coordination. Nature neuroscience, 5(11), 1226-1235. • Todorov, E. (2005). Stochastic optimal control and estimation methods adapted to the noise characteristics of the sensorimotor system. Neural computation, 17(5), 1084-1108. • Athans, M. (1967). The matrix minimum principle. Information and control, 11(5), 592-606. • Phillis, Y. A. (1985). Controller design of systems with multiplicative noise. Automatic Control, IEEE Transactions on, 30(10), 1017-1019. • Qian, N., Jiang, Y., Jiang, Z. P., & Mazzoni, P. (2013). Movement duration, fitts's law, and an infinite-horizon optimal feedback control model for biological motor systems. Neural computation, 25(3), 697-724. • Diedrichsen, J. (2007). Optimal task-dependent changes of bimanual feedback control and adaptation. Current Biology, 17(19), 1675-1679. • Izawa, J., Rane, T., Donchin, O., & Shadmehr, R. (2008). Motor adaptation as a process of reoptimization. The Journal of Neuroscience, 28(11), 2883-2891. • Nashed, J. Y., Crevecoeur, F., & Scott, S. H. (2014). Rapid online selection between multiple motor plans. The Journal of Neuroscience, 34(5), 1769-1780.
- 28. Exercise • Write a Matlab code of the minimum-variance model for a trajectory with given initial and final positions. • Write a Matlab code of the optimal feedback control for a trajectory with given initial and final positions. • Investigate how the minimum-variance model and the optimal feedback model differ.