ders 8 Quantile-Regression.ppt

Quantile Regression
 Assoc Prof Ergin Akalpler
 erginakalpler@csu.edu.tr

Quantile regression
 QR is an extension of linear regression. It is an used
when the conditions of LR are not met like linearity
homoscedasticity and normality. The quantile
regression has stronger distributional assumptions.
 HO= there is no significant impact on LnX LnY or LnZ
variables.
 LnY is statistically significant since P value is less than
0.05. If there is an increase in one percent median
value of LnY then Ln X will increase by 1/3 percent
 And in the median value LnZ in not significiant since P
value is greater than 0.05.

Regression is a statistical method broadly used in
quantitative modeling.
Multiple linear regression is a basic and standard
approach in which researchers use the values of several
variables to explain or predict the mean values of a scale
outcome.
However, in many circumstances, we are more interested
in the median, or an arbitrary quantile of the scale
outcome.

•Quantile regression models the relationship between a
set of predictor (independent) variables and specific
percentiles (or "quantiles") of a target (dependent)
variable, most often the median.
•It has two main advantages over Ordinary Least
Squares regression:
•Quantile regression makes no assumptions about the
distribution of the target variable.
•Quantile regression tends to resist the influence of
outlying observations
Quantile regression is widely used for researching in
industries such as ecology, healthcare, and financial
economics.

Quantile Regression
Linear vs non-linear model
Why QR
Graphical representation
Application
Practical example

Ordinary least squares (OLS) models focus on the mean,
E(Y|X) or the conditional expectation function (CEF).
Applied economists increasingly want to know what is
happening to an entire distribution, which can be
achieved using quantile regression (QR).
Quantiles divide or partition the number of
observations in a study into equally sized groups,
such as
Quartiles (divisions into four groups),
quintiles (division into five groups),
deciles (division into ten equal groups),
and centiles or percentiles (division into 100 equal
groups).
For more pls read Damodar Gujarati

Linear Regression is used to relate the
Conditional Mean to predictors.
Quantile Regression
relates specific quantiles to predictors.
Particularly useful with non-normal data Makes
use of different loss function than Ordinary
Least Squares – Uses linear programming to
estimate

Standard linear regression techniques summarize the
average relationship between a set of regressors and the
outcome variable based on the conditional mean function
E(y|x).
This provides only a partial view of the relationship, as we
might be interested in describing the relationship at
different points in the conditional distribution of y.
Quantile regression provides that capability. Analogous to
the conditional mean function of linear regression,
we may consider the relationship between the regressors
and outcome using the conditional median function
Qq(y|x), where the median is the 50th percentile, or
quantile q, of the empirical distribution.

Concept of non-linearity
 Nonlinearity is a term used in statistics to describe a
situation where there is not a straight-line or direct
relationship between an independent variable and a
dependent variable.
 In a nonlinear relationship, changes in the output do
not change in direct proportion to changes in any of
the inputs.
 Nonlinearity is a mathematical term describing a
situation where the relationship between an
independent variable and a dependent variable is not
predictable from a straight line.

What is nonlinear model?
 In general nonlinearity in regression model can
be seen as:
Nonlinearity of dependent variable ( y )
Nonlinearity within independent variables (x’s)

How to detect nonlinearity?
 1. Theory – in many sciences we have theories about
 nonlinear relations within some phenomenon. For
example:
 in economics Laffer curve shows a nonlinear relations
 between taxation and the hypothetical resulting levels
of government revenue
 2. Scatterplot – when looking at the plot you can see
that data points are not linear or not linear.

 3. Seasonality in data – i.e. in agriculture,
building industry we often have seasonality
within the data
 4. Estimated model does not fit the data
well or does not fit. it at all; the estimated
β’s are not significant – this might suggest
nonlinearity
How to detect nonlinearity?

Linear or nonlinear? – That is the question

Linear or nonlinear? – That is the
question

Linear or notlinear? – That is the question

Why Quantile Regression?
 Quantile regression allows us to study the impact of
independent variables on different quantiles of
dependent variable's distribution,
 It provides a complete picture of the relationship
between Y and X.
 Robust to outliers in y observations.
 Estimation and inferences are distribution-free.
 Analysis of distribution rather than average
 Quantile regression allows for effects of the
independent variables to differ over the quantiles.
17

Introduction
18
 First proposed by Koenker and Bassett (1978),
quantile regression is an extension of the classical
least squares estimation.
 OLS regression only enables researchers to
approximate the conditional mean and median
located at the centre of the distribution.
 Quantile regression is applied when an estimate of
the various quantiles in a population is desired.

Cont..
 Classical linear regression estimates the mean
response of the dependent variable dependent on the
independent variables.
 There are many cases, such as skewed data,
multimodal data, or data with outliers,
 when the behavior at the conditional mean fails to
fully capture the patterns in the data.

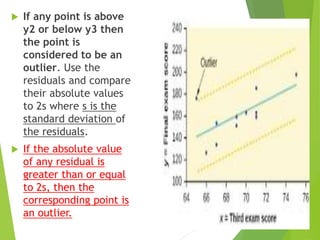
Outliers
Info : Outliers: in regression are observations that
fall far from the "cloud" of points.
 These points are especially important because they
can have a strong influence on the least squares line.
If the absolute value of any residual is greater than or
equal to 2s (2st. dev.), then the corresponding point is an
outlier.

 If any point is above
y2 or below y3 then
the point is
considered to be an
outlier. Use the
residuals and compare
their absolute values
to 2s where s is the
standard deviation of
the residuals.
 If the absolute value
of any residual is
greater than or equal
to 2s, then the
corresponding point is
an outlier.

Cont..
 Common regression methods measure differences in
outcome variables between populations at the mean
(i.e., ordinary least squares regression), or a
population average effect after adjustment for other
explanatory variables of interest.
 The Quantile regression (QR) method is more robust
to outliers (Oliveira et al., 2013).
 These are often done assuming that the regression
coefficients are constant across the population.
 In other words, the relationships between the
outcomes of interest and the explanatory variables
remain the same across different values of the
variables.

Cont..
The distribution of Y, the “dependent” variable,
conditional on the covariate X, may have thick
tails.
The conditional distribution of Y may be
asymmetric.
Regression will not give us robust results.
Outliers are problematic, the mean is pulled
toward the skewed tail.
OLS are sensitive to the presence of outliers.

Cont..
24
 An outlier is an observation point that is distant from other
observations.
 An outlier can cause serious problems in statistical
analyses.
 The impact of income on consumption is conditional on
mean it may give misleading results
 if conditional on different quantiles, it will capture outlier in
consumption too like in Ramadan the consumption is high
compare to other months, same christmas and Chines new
year

Cont..
25
 While the quantile regression estimator minimizes the
weighted sum of absolute residuals rather than the sum of
squared residuals, and thus the estimated coefficient
vector is not sensitive to outliers.
 The quantile regression approach can thus obtain a much
more complete view of the effects of explanatory variables
on the dependent variable.

Cont..
 When to employ quantile regression:
 Histogram not normal distribution is desired and P
value is less than 0.05
 LM test result: P value must be less than 0.05
 Heteroskedasticity result: P value must be less than
0.05


Cont..
 When to employ OLS regression:
 Histogram normal distribution is desired and P
value is more than 0.05
 LM test results: no serial correlation, P value
must be more than 0.05
 Heteroskedasticity no needed and results: P
value must be more than 0.05


Reasons to use quantiles rather than
means
 Analysis of distribution rather than average
 Robustness
 Skewed data
 Interested in representative value
 Interested in tails of distribution
 Unequal variation of samples
 E.g. if income distribution is highly skewed i.e.
high low and middle, then mean based coefficient
cannot capture the accurate distribution of the
income.

Comparison Quantile regression with OLS
A statistical model that utilizes one quantitative independent
variable “X” to predict the quantitative dependent variable “Y.”
 Linearity - the Y variable is linearly related to the value of
the X variable.
 Independence of Error - the error (residual) is independent
for each value of X.
 Homoscedasticity - the variation around the line of regression
be constant for all values of X.
 Normality - the values of Y be normally distributed at each
value of X.

What are the 5 assumptions of regression?
The regression has five key assumptions:
• Linear relationship.
• Multivariate normality.
• No or little multicollinearity.
• No auto-correlation.
• Homoscedasticity.

Best OLS -regression model
null, Ho= residuals are not serially corelated
alt, H1= residuals are serially corelated
R2 value must be high
(it should be 60% and more for good model)
No serial correlation
(LM test probability value must be higher than 0.05 )
No hetroscedasticity
(in the residual p value must be highe than 0.05)
Residual are normally distributed
(histogram p value must be higher than 0.05)

When should I use quantile regression?
Quantile regression is an extension of linear
regression that is used
when the conditions of linear regression are not
met
linearity,
homoscedasticity,
independence,
normality

 Best quantile regression model
null, Ho= residuals are serially corelated
alt, H1= residuals are serially corelated
 R2 value is not the relevant for QR
 (How “Variability explained" (as measured in terms of
variances, anyway) is essentially a least-squares concept;
Important is to find what is an appropriate measure of
statistical significance or possibly goodness of fit among
variables.)
 serial correlation
(LM test probability value must be less than 0.05 )
 No hetroscedasticity
(in the residual p value must be less than 0.05)
Residual are not normally distributed
(histogram p value must be less than 0.05)

Quantile regression r squared value
meaning
 The goodness of fit of quantile regression:
 The pseudo or (spurious) R squared value is assumed
to be 29 % the adjusted R squared value is 27%.
 So 27 percent variation in the conditional median in
LnX is due to LnY.
 Quasi Least squared statistic value
 is 29.34 and probability value is less than 0.05 which
indicates that model is stable.

Advantages of quantile regression (QR)
•while OLS can be inefﬁcient if the errors are highly non-
normal, QR is more robust to non-normal errors and
outliers.
•QR also provides a richer characterization of the data,
allowing the researchers to consider the impact of a
covariate on the entire distribution of y, not merely its
conditional mean.

How to do
1-First estimate a QR for the 50th quantile (the median).
2. Then estimate a QR for the 25th (i.e. the first quartile)
and the 75th quantile (i.e. the third quartile) simultaneously.
3. Compare the QRs estimated in (2) with the OLS regression.
4. One possible reason that the coefficients may differ across
quantiles is the presence of heteroscedastic errors.
5. The estimated quantile coefficients may look different for
different quantiles.
To see if they are statistically different, we use the Wald
test. We can use the Wald test to test the coefficients of a
single regressor across the quantiles or we can use it to test
the equality of the coefficients of all the regressors across
the various quantiles. Damodar Gujarati

ders 8 Quantile-Regression.ppt

38
0
.1
.2
.3
.4
Fraction
-20 0 20 40 60
netinterestmargin
As we see that the shape of interest margin is leptokurtic which is not
captured by normal distribution-based models the mean is pulled toward the
skewed tail.

41
 As the classical linear regression i.e. OLS estimator
only focuses on mean value while QR defines data in
a better way as it analyses the level of interest margin
by quantiles.
 Thus, the quantile regression is an extension of the
classical regression model to estimate conditional
quantile functions.
 QR is super over other usual mean value regressions
as it allows for the analysis of different levels or
thresholds of a dependent variable.

42
 Thank YOU
 eakalpler@gmail.com
 erginakalpler@csu.edu.tr
 YouTube: ERGIN FIKRI AKALPLER watch your related
course videos

ders 8 Quantile-Regression.ppt

More Related Content

ders 8 Quantile-Regression.ppt

Editor's Notes