Location via proxy:   [ UP ]  
[Report a bug]   [Manage cookies]                
Scribd Logo
Upload

Welcome to Scribd!

  • 13 views

    ENEE 322 Due in Discussion Week of Feb. 4, 2013 Homework 01

    Uploaded by

    Serge Mandhev Swamotz
    This document contains instructions for homework assignment 01 for the course ENEE 322. It includes problems on expressing complex numbers in polar and Cartesian forms, finding the even and odd components of signals, sketching signals defined by unit step functions, determining if signals are periodic and finding their fundamental periods, and using trigonometric identities and Euler's formula. Additional optional problems are provided but not to be turned in.

    Copyright:

    Attribution Non-Commercial (BY-NC)
    Download as PDF, TXT or read online from Scribd

    ENEE 322 Due in Discussion Week of Feb. 4, 2013 Homework 01

    Uploaded by

    Serge Mandhev Swamotz
    13 views2 pages
    This document contains instructions for homework assignment 01 for the course ENEE 322. It includes problems on expressing complex numbers in polar and Cartesian forms, finding the even and odd components of signals, sketching signals defined by unit step functions, determining if signals are periodic and finding their fundamental periods, and using trigonometric identities and Euler's formula. Additional optional problems are provided but not to be turned in.

    Original Title

    hw01

    Copyright

    © Attribution Non-Commercial (BY-NC)

    Available Formats

    PDF, TXT or read online from Scribd

    Did you find this document useful?

    Is this content inappropriate?

    This document contains instructions for homework assignment 01 for the course ENEE 322. It includes problems on expressing complex numbers in polar and Cartesian forms, finding the even and odd components of signals, sketching signals defined by unit step functions, determining if signals are periodic and finding their fundamental periods, and using trigonometric identities and Euler's formula. Additional optional problems are provided but not to be turned in.

    Copyright:

    Attribution Non-Commercial (BY-NC)
    Download as PDF, TXT or read online from Scribd
    Download as pdf or txt
    13 views2 pages

    ENEE 322 Due in Discussion Week of Feb. 4, 2013 Homework 01

    Uploaded by

    Serge Mandhev Swamotz
    This document contains instructions for homework assignment 01 for the course ENEE 322. It includes problems on expressing complex numbers in polar and Cartesian forms, finding the even and odd components of signals, sketching signals defined by unit step functions, determining if signals are periodic and finding their fundamental periods, and using trigonometric identities and Euler's formula. Additional optional problems are provided but not to be turned in.

    Copyright:

    Attribution Non-Commercial (BY-NC)
    Download as PDF, TXT or read online from Scribd
    Download as pdf or txt
    You are on page 1of 2

    ENEE 322

    Due in Discussion Week of Feb. 4, 2013

    Homework 01

    1. Express each of the following complex numbers in polar form (rej with < ). (a) S1 = 4 (b) S2 = (1 j)2 (c) S3 = 2+j 2 1+j 3

    2. Find the even and odd components of the following signals: (a) x(t) = cos(2t) + sin(2t) + sin(2t) cos(2t) (b) y(t) = 1 + t + 3t2 + 5t3 + 9t4 (c) z(t) = t, 0, 0t2 otherwise

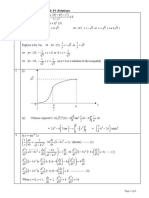
    3. Sketch the following signals (a) xa (t) = u(t 5) u(t 7) (b) xb (t) = u(t 5) + u(t 7) (c) xc (t) = t2 [u(t 1) u(t 2)] (d) xd (t) = (t 4) [u(t 2) u(t 4)] 4. Determine whether or not each of the following signals is periodic, and if periodic nd the fundamental period. Also, use Matlab to plot the signals. (a) xa (t)] = cos2 (b) xb (t) = cos (c) xc (t) = e2t
    2

    t 3 2 t 3

    (d) xd [n] = cos2 (e) xe [n] = cos (f) xf [n] = e2n

    n 3 2 n 3
    2

    Additional Problems. Do Not Turn In!!


    5. Express each of the following complex numbers in Cartesian form (x + jy).
    1 (a) Z1 = 2 ej

    (b) Z2 = ej/2 (c) Z3 = ej5/2 (d) Z4 = 2ej9/4 6. Use Eulers identities to prove the following trigonometric identities (a) sin(2) = 2 sin cos
    1 (b) cos2 = 2 (1 + cos 2)

    (c) sin( + ) = sin cos + cos sin

    You might also like