Required knowledge and skills: linear functions

Overview
1. Linear function: function whose equation is linear, i.e. has the form
b mx y + =
, where 0 m
2. Graph of a linear function: straight line
a. drawing the graph when the equation is given
b. setting up the equation when the graph is given (see also item !
". #nterpretation of the coefficient m in the equation
b mx y + =
a. slope of the line
b. rate of change: if x increases b$ 1 unit, then y changes b$ m units
c. difference quotient:
1 2
1 2
x x
y y
x
y
m

=
, where P
1
! , (
1 1
y x and P
2
! , (
2 2
y x are points on the
line
d. sign of m determines whether line is increasing or decreasing
e. absolute value of m determines how steep the line is
f. parallel lines have equal slopes
g. slopes of perpendicular lines have product equal to %1
&. #nterpretation of the coefficient b in the equation
b mx y + =
a. b is y'intercept
b. b is function value of 0
c. 0 = b iff origin is on the line
. (etting up the equation of a line
a. if slope m and one point P ! , (
0 0
y x are given: ! (
0 0
x x m y y =
b. if two points are given
). Linear equations:
a. solving linear equations
b. solving other equations leading to a linear equation
c. (graphical! interpretation of the solution of a linear equation: solution of equation 0 = + b mx
i. is x'intercept of the corresponding line
ii. is the *ero of the corresponding linear function
+. Linear inequalities
a. solving linear inequalities
b. graphical interpretation of linear inequalities
i. solutions of 0 > + b mx form interval where corresponding line is above the hori*ontal a,is
ii. solutions of
2 2 1 1
b x m b x m + > + form interval where the line corresponding to left hand side
is above the line corresponding to right hand side
-. #mplicit equation of a line:
0 = + + c by ax
or, equivalentl$,
d by ax = +
, (where a and b are not
simultaneousl$ 0!. hori*ontal and vertical lines
/. Graphical interpretation of the solution of a s$stem of two linear equations: intersection point of the
lines corresponding to the equations
10. 0pplications and word problems involving linear functions, more specificall$: setting up an equation
for one or more linear functions given a description in words and using these equations to solve a
1
problem b$ calculating a function value, solving a linear equation, solving a linear inequalit$, solving
a s$stem of linear equations, 1
Examples
2,ample 1. 3hich of the following functions are linear4 5oreover, in case the function is linear, find out
whether the function is increasing or decreasing.
0.
"
x y =
6.
x y " =
7.
" = x y
8.
= y
2.
! " ( 2 = x y
9.
! " ( = x x y
G.
2
" ! " ( x x x y =
:.
" = x y
2,ample 2. 9ind the equation of the line through the points
! 1 , 2 ( P
and
! 2 , 1 ( Q
.
2,ample ". 9ind the equation of the line through the point
! 1 , 2 ( P
and parallel to the line through
! 2 , ( Q
and
! . & , 0 ( R
.
2,ample &. 9ind the equation of the line through the origin and perpendicular to the line having equation
" 2 + = x y
.
2,ample . 0re the lines
& " 2 = + y x
and
& 2 " = y x
perpendicular to each other4
2,ample ). 9ind the intersection point of the lines
& " 2 = + y x
and
& 2 " = y x
.
2,ample +. ;he cost of c of producing q units of a certain good consists of two parts. ;here is a fi,ed cost
of 2-0 2<=, plus a variable cost of " 2<= per unit produced. 3rite an equation giving the cost c in terms
of the number q of units produced.
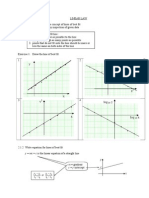
2,ample -. 0 new product was launched in 200&. ;he graph below shows how man$ units of this product
were sold in the $ears 200& to 200+. #f the sales continue increasing in the same wa$, how man$ units of
the product will be sold in 20104
2,ample /. ;he cost c of a ta,i ride of x >m is given b$ the equation x c - . 0 + = . 5a>e a graph
showing the price of ta,i rides for a distance between 0 and 10 >m.
2,ample 10. 0 first electricit$ compan$ charges a fi,ed rate of 100 2<= per $ear and 0.2 2<= per
>ilowatt'hour of electricit$ consumed. 0 second compan$ has no fi,ed rate, but charges 0.22 2<= per
2
>ilowatt'hour consumed. 9ind out for which $earl$ consumption of electricit$ the second compan$ is
cheaper than the first one.
Solutions to the examples
2,ample 1. 6 (increasing!, 7 (increasing!, 2 (decreasing!, G (decreasing!, : (increasing!
2,ample 2.
" + = x y
2,ample ".
2 . 0 + = x y
2,ample &.
x y . 0 =
2,ample . $es
2,ample ). intersection point has coordinates

1"
&
,
1"
20
2,ample +.
q c " 2-0 + =
2,ample -. 1) 000
2,ample /. see graph below
2,ample 10. $earl$ consumption below 000 >ilowatt'hours
3