Chem 150 PS1 2014

1
Due: Thursday, Feb 06

Chemistry 150
Problem Set 1

1) a) Consider a face centered cubic array of chloride ions with sodium atoms occupying
the octahedral holes (i.e. the NaCl structure type). The diagram below shows a planar
{100} slice of the NaCl structure with four chloride ions in contact with each other as
well as the central sodium ion. Using r
x
to denote the radius of the chloride ions and
r
m
to denote the sodium ion radius, derive the necessary radius ratio (r
m
/r
x
) for all
nearest neighbor atoms to remain in contact.

b) Would a structure be more likely to adopt the NaCl structure type if its r
m
/r
x
radius
ratio were larger or smaller than the one you calculated above? Explain briefly what
a smaller or larger ratio means physically.

c) Derive the minimum radius ratio (r
m
/r
x
) possible for a cation in contact with eight
anions in the CsCl structure type.

d) Which is more likely to follow the radius ratio rules, AuCl or KCl? Why?

2) Powder x-ray diffraction is an invaluable tool for analysis of solid-state structure and
purity. In this technique, a polycrystalline sample is exposed to a beam of x-rays. Planes
of atoms within the sample will diffract the beam when the Bragg equation is satisfied
(2dsin! = n!) where d is the distance between lattice planes, ! is the angle between the
incoming x-ray beam and the diffraction plane, ! is the wavelength of the radiation
source, and n is the order of the diffraction.

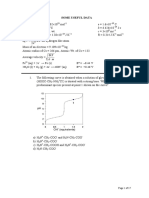
Plutonium has been called the most complex element on the periodic table
1
because six
different crystalline phases have been reported at various temperatures. For instance, the
" phase of plutonium metal is a face centered cubic crystalline solid that is stable between
~600 to 700 C. Shown below is the powder x-ray diffraction pattern of " phase
plutonium.

1
Sderlind, Per; Sadigh, Babak. Phys. Chem. Rev. (2004) 92.
2
Powder X-ray diffraction Pattern of Plutonium (delta phase)
0 10 20 30 40 50 60 70 80 90 100
2! (deg)
I
n
t
e
n
s
i
t
y
t
y
2! = 38.80
2! = 83.28
2! = ??

a) Draw a unit cell for "-Pu and sketch in a (111), (100), and (110) lattice plane.

b) Fill in the missing data in the following table where 2! is the full diffraction angle, d
(#) is the distance between planes and h, k, and l are Miller indices. [NOTE: all
peaks are the result of first order diffraction (n=1), and the x-ray source is CuK$
1
(! =
1.540598 )].

2! (deg) d (!) h k l
1 1 1
38.80 2 0 0
83.28 0 0

c) What is the volume of the cell?

d) The (200) peak is the second largest peak for "-Pu. Where are the peaks for the (020),
(002), (02 0), and (002 ) sets of lattice planes?

e) Based on the atomic arrangement of the fcc cell, make a qualitative argument as to
why the (111) peak is more intense than the (200) peak.

f) Calculate the crystallographic density of "-Pu in units of g/cm
3
.

3) A tube furnace with a platinum heating element is heated to very high temperatures for
long periods of time under an atmosphere of O
2
. Eventually platinum crystals begin to
form near the outer edges of the furnace. Write a chemical equation and brief
explanation of why the crystals are forming. Your explanation should include the vant
Hoff equation.

Pt(s) + O
2
(g) PtO
2
(g)

3
4) Consider the following (unbalanced) solid state reaction:

a) In the product, oxygen atoms form an fcc lattice with Mg occupying one eighth of the
tetrahedral sites and Fe occupying half of the octahedral sites. Given this information,
what is the correct formula for the product compound?

b) Despite a strong thermodynamic favorability, this reaction does not occur under
standard conditions. Why is this, and what synthetic methods could be employed to
make the reaction occur?

c) The diagram below shows the interface between two reactant crystals before, and
after, the reaction has begun. Write balanced equations for the reactions at each
interface such that they add to form the overall reaction. Be sure to account for the
ions being transported through the product lattice to the other interface by subtracting
them from your equations.

d) The rates of product growth at the interfaces are not equal; what ratio would you
predict between the rates of growth at interface I and interface II?

5) Consider an infinite one-dimensional chain of equally spaced hydrogen atoms. The band
diagram for such a structure is shown below. (Note: the unit cell has been chosen to
include 2 hydrogen atoms).

MgO(s) + Fe
2
O
3
(s) Mg
x
Fe
y
O
4
(s)
4
a) Write the form of %
n
for for the bands labeled i) and ii) using the Hckel
approximation (hint: these are just the molecular orbitals of H
2
).

b) What is the range of k in the band diagram?

c) Using a representative three unit cells for each, draw in the phases of the 1s orbitals at
locations i, ii, and iii on the band diagram

d) In reality, hydrogen does not form infinite one dimensional chains. Draw a new band
diagram showing the effect of shortening one H-H bond and lengthening the other to
form separate H
2
molecules.

e) How is this distortion similar to what happens to copper (II) in an octahedral
environment?

6) Consider a linear chain of eclipsed PtH
4
2-
units as depicted below.

a) The diagram to the left depicts the bands of
some of the orbitals of the platinum metal.
Label the orbitals which compose each of the
bands shown. (Hint: only bands corresponding
to the platinum d orbitals and the platinum p(z)
orbital are shown).

b) Why do some bands run up from k = 0 to k =
&/a and some run down?

c) Which d orbital band has the most dispersion
(largest bandwidth)? Explain this in terms of
its bonding.

d) Using four repeat units of the structure, draw
the p(z) band at k = 0 and k = &/a.

e) Where is the Fermi level for this one
dimensional structure? Would you predict it to
be a conductor or an insulator?

5
f) Say the platinum is partially oxidized (~0.3 less electrons per Pt on average). How
would this change the conductive properties? Would you predict the Pt Pt distance
to increase, decrease, or remain the same?

7) Consider an infinite two dimensional sheet of hydrogen atoms.

a) On separate 4 x 4 grids draw pictorial representations of the 1s orbital phases at ', (,
and M.

b) Order (, ', and M from lowest to highest energy.

c) Label them as bonding, non-bonding, or antibonding.

8) Decide whether or not the following systems are likely to be p-type or n-type
semiconductors.

a) As-doped Ge

b) Ga-doped Ge

c) Si-doped Ge

Chem 150 PS1 2014

Uploaded by

Copyright:

Available Formats

Chem 150 PS1 2014

Uploaded by

Document Information

Original Description:

Original Title

Copyright

Available Formats

Share this document

Share or Embed Document

Sharing Options

Did you find this document useful?

Is this content inappropriate?

Copyright:

Available Formats

Chem 150 PS1 2014

Uploaded by

Copyright:

Available Formats

1

Due: Thursday, Feb 06

You might also like