0 ratings0% found this document useful (0 votes)
124 viewsMathematical Morphology
Mathematical Morphology
Uploaded by
Eng M G ElkhateebThis document provides an overview of mathematical morphology concepts and operations for binary images. It introduces morphological operations like dilation, erosion, opening, and closing that can be used to modify image shapes and sizes. Dilation expands objects while erosion shrinks them. Opening and closing combine these to smooth contours or fill small holes. Structuring elements are used to specify the shape of these operations. The document describes techniques like boundary detection, noise removal, region filling, and skeletonization that apply morphological operations. Example MATLAB code is provided to demonstrate the techniques.
Copyright:
© All Rights Reserved
Available Formats
Download as PDF, TXT or read online from Scribd
Mathematical Morphology
Mathematical Morphology
Uploaded by
Eng M G Elkhateeb0 ratings0% found this document useful (0 votes)
124 views8 pagesThis document provides an overview of mathematical morphology concepts and operations for binary images. It introduces morphological operations like dilation, erosion, opening, and closing that can be used to modify image shapes and sizes. Dilation expands objects while erosion shrinks them. Opening and closing combine these to smooth contours or fill small holes. Structuring elements are used to specify the shape of these operations. The document describes techniques like boundary detection, noise removal, region filling, and skeletonization that apply morphological operations. Example MATLAB code is provided to demonstrate the techniques.
Original Description:
Lecture
Copyright
© © All Rights Reserved
Available Formats
PDF, TXT or read online from Scribd
Share this document
Did you find this document useful?
Is this content inappropriate?
This document provides an overview of mathematical morphology concepts and operations for binary images. It introduces morphological operations like dilation, erosion, opening, and closing that can be used to modify image shapes and sizes. Dilation expands objects while erosion shrinks them. Opening and closing combine these to smooth contours or fill small holes. Structuring elements are used to specify the shape of these operations. The document describes techniques like boundary detection, noise removal, region filling, and skeletonization that apply morphological operations. Example MATLAB code is provided to demonstrate the techniques.
Copyright:
© All Rights Reserved
Available Formats
Download as PDF, TXT or read online from Scribd
Download as pdf or txt
0 ratings0% found this document useful (0 votes)
124 views8 pagesMathematical Morphology
Mathematical Morphology
Uploaded by
Eng M G ElkhateebThis document provides an overview of mathematical morphology concepts and operations for binary images. It introduces morphological operations like dilation, erosion, opening, and closing that can be used to modify image shapes and sizes. Dilation expands objects while erosion shrinks them. Opening and closing combine these to smooth contours or fill small holes. Structuring elements are used to specify the shape of these operations. The document describes techniques like boundary detection, noise removal, region filling, and skeletonization that apply morphological operations. Example MATLAB code is provided to demonstrate the techniques.
Copyright:
© All Rights Reserved
Available Formats
Download as PDF, TXT or read online from Scribd
Download as pdf or txt
You are on page 1of 8
CCU CCU
7SDN 7SDN
LA8DFATDFY LA8DFATDFY
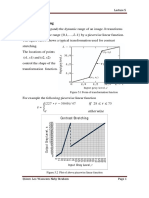
Introduction to
Image Processing
Lecture Set 10
Chapter 10: Mathematical Morphology
H.Y.LIn, CCUEE ntroductIon to mage ProcessIng
Binary Image Morphology
The word morphology refers to form and structure
In image processing and computer vision, it can be used
to refer to the shape of a region
The operations of mathematical morphology were
originally defined as set operations
Morphological operators can:
Thin,
Thicken,
Find boundaries,
Find skeletons (medical axis),
Convex hull,
And more
H.Y.LIn, CCUEE ntroductIon to mage ProcessIng
Structuring Llements
The operations of binary morphology input a binary
image B and a structuring element S
The structuring element S is usually another smaller
binary image
It represents a shape
It can be any size and have arbitrary structure that can be
represented by a binary image
Some common structuring elements
1 1 1
1 1 1
1 1 1
1 1 1 1 1
1 1 1 1 1
1 1 1 1 1
1 1 1
1 1
1 1
1 1
1 1 1
1 1 1
1 1 1 1 1
1 1 1 1 1
1 1 1 1 1
1 1 1
1
1
1
1
1
H.Y.LIn, CCUEE ntroductIon to mage ProcessIng
Point Sets and Notation
Binary objects are considered as point sets
For point sets A and B denote the:
Translation of A by x as A
x
= {a
i
+ x | a
i
A}
Figure 10.1, page 262, textbook
Reflection of B as B
r
= {-b
i
| b
i
B}
Figure 10.2, page 262, textbook
Complement of A as A
c
= {a
i
| a
i
A}
Example ?
Difference of A and B as A B = {c
i
| (c
i
A) XOR (c
i
B)}
Example ?
H.Y.LIn, CCUEE ntroductIon to mage ProcessIng
Basic Operations
The basic operations of binary morphology are dilation,
erosion, closing, and opening
Dilation enlarges a region
Erosion makes a region smaller
A closing operation can close up internal holes in a region and
eliminate bays along the boundary
An opening operation can get rid of small portions of the region
that just out from the boundary into the background region
Some applications
Binary morphology can be used to extract primitive features of
an object that can be used to recognize the object
A shape matching system can use morphological feature
detection to rapidly detect primitives that are used in object
recognition
H.Y.LIn, CCUEE ntroductIon to mage ProcessIng
Dilation
Dilation of B by structuring element S:
B S = {x
i
| (S
x
r
B) )} =
bB
S
b
Example: dilating A with a 33 structuring element B
centered at the origin
Example: Figure 10.3, page 264, textbook
B
S
H.Y.LIn, CCUEE ntroductIon to mage ProcessIng
Lxample - MA1LAB, p265.m
t = imread('text.tif');
sq = ones(3,3);
td = imdilate(t,sq);
subplot(1,2,1),imshow(t)
subplot(1,2,2),imshow(td)
H.Y.LIn, CCUEE ntroductIon to mage ProcessIng
Lrosion
Erosion of B by structuring element S:
B S = {x
i
| S
x
B} = {b | b + s B, s S}
Example: eroding A with a 33 structuring element B
centered at the origin
Example: Figure 10.6, page 267, textbook
B
S
H.Y.LIn, CCUEE ntroductIon to mage ProcessIng
Lxample - MA1LAB, p266.m
c = imread('circbw.tif');
ce = imerode(c,sq);
subplot(1,2,1),imshow(c)
subplot(1,2,2),imshow(ce)
H.Y.LIn, CCUEE ntroductIon to mage ProcessIng
Announcements - 5,3,06
See some demos
H.Y.LIn, CCUEE ntroductIon to mage ProcessIng
Application - Boundary Detection
boundary(B,S) = B B S
External boundary: (B S) B
Morphological gradient: (B S) (B S)
Example : Figure 10.9, page 270, textbook
S
erosion difference
boundary(B,S)
B
H.Y.LIn, CCUEE ntroductIon to mage ProcessIng
Lxample - MA1LAB, p21.m
rice = imread('rice.tif');
r = rice > 110;
re = imerode(r,sq);
r_int = r&~re;
subplot(1,2,1),imshow(r)
subplot(1,2,2),imshow(r_int)
rd = imdilate(r,sq);
r_ext = rd&~r;
r_grad = rd&~re;
figure
subplot(1,2,1),imshow(r_ext)
subplot(1,2,2),imshow(r_grad)
H.Y.LIn, CCUEE ntroductIon to mage ProcessIng
Combining Dilation and Lrosion
Combining dilation and erosion for
Opening
Closing
Thickening
Thinning
Skeleton
H.Y.LIn, CCUEE ntroductIon to mage ProcessIng
Intuitie Interpretation
Dilation expands an object
Erosion contracts an object
Opening
Smoothes contours
Enlarges narrow gaps
Eliminates thin protrusions
Closing
Fills narrow gaps, holes and small breaks
H.Y.LIn, CCUEE ntroductIon to mage ProcessIng
Opening
Opening: Like smoothing from the inside
B S = (B S) S = {S
x
| S
x
B}
Example: Figure 10.12, page 273, textbook
S
erosion dilation
open(B,S)
B
H.Y.LIn, CCUEE ntroductIon to mage ProcessIng
Closing
Closing: Like smoothing from the outside
B S = (B S) S
Example: Figure 10.13, page 274, textbook
S
dilation erosion
close(B,S)
B
H.Y.LIn, CCUEE ntroductIon to mage ProcessIng
More Lxample
Dilation
Erosion
Opening
Closing
H.Y.LIn, CCUEE ntroductIon to mage ProcessIng
Idempotency
Applying opening or closing more than once has
no further effect
open(open(A,B),B) = open(A,B)
close(close(A,B),B) = close(A,B)
H.Y.LIn, CCUEE ntroductIon to mage ProcessIng
MA1LAB - p24.m
sq = ones(3,3);
cr = [0 1 0; 1 1 1; 0 1 0];
test = zeros(10,10);
test(2:6,2:4) = 1;
test(3:5,6:9) = 1;
test(8:9,4:8) = 1;
test(4,5) = 1
imopen(test,sq)
imopen(test,cr)
imclose(test,sq)
imclose(test,cr)
t = imread('text.tif')
diag=[0 0 1; 0 1 0; 0 0 1]
tc = imclose(t,diag);
imshow(tc)
H.Y.LIn, CCUEE ntroductIon to mage ProcessIng
Application - Noise Remoal
Morphological filtering (page 276, textbook)
((A B) B) = (((A B) B) B) B
Erosion, dilation, dilation, erosion
H.Y.LIn, CCUEE ntroductIon to mage ProcessIng
MA1LAB - p2.m
c = imread('circles.tif');
x = rand(size(c));
d1 = find(x<=0.05);
d2 = find(x>=0.95);
c(d1) = 0;
c(d2) = 1;
imshow(c)
cf1 = imclose(imopen(c,sq),sq);
figure, imshow(cf1)
cf2 = imclose(imopen(c,cr),cr);
figure, imshow(cf2)
H.Y.LIn, CCUEE ntroductIon to mage ProcessIng
Additional Structuring Operations
Find boundary of an object
Region filling
Connected component (More on next chapter)
Skeletonization (More on next chapter)
H.Y.LIn, CCUEE ntroductIon to mage ProcessIng
Region lilling
Problem:
Fill 8-connected boundary A with 1s given a point inside
the boundary p
Use structuring element S, and
Iterative dilations
Complement
Intersection
S
B
p
H.Y.LIn, CCUEE ntroductIon to mage ProcessIng
Region lilling
Let C
0
= p
Calculate
C
k
= (C
k-1
S) B
c
, for k = 1,2,
Stop when C
k
= C
k-1
C
k
is the interior of B
Example:
Figures 10.21, 10.22, pages 280, 281, textbook
S
B
p
H.Y.LIn, CCUEE ntroductIon to mage ProcessIng
Region lilling - MA1LAB
function out=regfill(im,pos,kernel)
% REGFILL(IM,POS,KERNEL) performs region filling of binary image IMAGE,
% with kernel KERNEL, starting at point with coordinates given by POS.
%
% Example:
% n=imread('nicework.tif');
% nb=n&~imerode(n,ones(3,3));
% nr=regfill(nb,[74,52],ones(3,3));
%
current=zeros(size(im));
last=zeros(size(im));
last(pos(1),pos(2))=1;
current=imdilate(last,kernel)&~im;
while any(current(:)~=last(:)),
last=current;
current=imdilate(last,kernel)&~im;
end;
out=current;
H.Y.LIn, CCUEE ntroductIon to mage ProcessIng
Region lilling - p.283.m
n = imread('nicework.tif');
imshow(n), pixval on
figure, imshow(n)
nb = n &~imerode(n,sq);
figure, imshow(nb)
nf = regfill(nb,[74,52],sq);
figure, imshow(nf)
figure, imshow(nf|nb)
H.Y.LIn, CCUEE ntroductIon to mage ProcessIng
Connected Component - p.283.m
sq2 = ones(11,11);
nc = components(n,[57,97],sq);
figure, imshow(nc)
nc2 = components(n,[57,97],sq2);
figure,imshow(nc2)
H.Y.LIn, CCUEE ntroductIon to mage ProcessIng
Skeletonization
The skeleton of a binary object is a collection of
lines and curves that encapsulate the size and
shape of the object
Lantuejouls method
Table 10.1, Figure 10.28, page 285, textook
Figure 10.29, page 286, textbook
H.Y.LIn, CCUEE ntroductIon to mage ProcessIng
Lantejoul`s Implementation
function skel = imskel(image,str)
% IMSKEL(IMAGE,STR) - Calculates the skeleton
% of binary image IMAGE using
% structuring element STR. This function uses
% Lantejoul's algorithm.
%
skel=zeros(size(image));
e=image;
while (any(e(:))),
o=imopen(e,str);
skel=skel | (e&~o);
e=imerode(e,str);
end
H.Y.LIn, CCUEE ntroductIon to mage ProcessIng
MA1LAB - p286.m
sq = ones(3,3);
cr = [0 1 0; 1 1 1; 0 1 0];
n = imread('nicework.tif');
nk = imskel(n,sq);
imshow(nk)
nk2 = imskel(n,cr);
figure, imshow(nk2)
You might also like
- BusinessAnlyticsAss3finalDocument3 pagesBusinessAnlyticsAss3finalmachaa0% (1)
- Week 5 Exercises SolutionsDocument12 pagesWeek 5 Exercises SolutionsAbdul M100% (1)
- DFS Algorithm For GraphDocument4 pagesDFS Algorithm For GraphMayank ChauhanNo ratings yet
- Formula Sheet MidtermDocument3 pagesFormula Sheet Midtermtariqueshams66No ratings yet
- Cheat SheetDocument1 pageCheat SheetJan AertsNo ratings yet
- Quantum Computing - GruskaDocument390 pagesQuantum Computing - GruskaRaaj Chatterjee100% (1)
- Chapter 7 NotesDocument9 pagesChapter 7 Notesapi-292320998No ratings yet
- Practical UML - A Hands-On Introduction For DevelopersDocument2 pagesPractical UML - A Hands-On Introduction For DevelopersParaschiv TristanNo ratings yet
- Chapter 05Document19 pagesChapter 05bchang412No ratings yet
- 2018 School Competition Answer KeyDocument1 page2018 School Competition Answer KeyRitvik EllendulaNo ratings yet
- Chapter 5 PDFDocument11 pagesChapter 5 PDFMd. Ayub KhanNo ratings yet
- ECE 452: Computer Organization and DesignDocument9 pagesECE 452: Computer Organization and Designdermeister1988No ratings yet
- Mpi CheatsheetDocument1 pageMpi CheatsheetTabusca VladutNo ratings yet
- Rasterization TextureDocument85 pagesRasterization TextureJoel MyersNo ratings yet
- CPU Organization Bindu AgarwallaDocument22 pagesCPU Organization Bindu AgarwallaNobodyNo ratings yet
- CSE331 - 211 Midterm Question Day PDFDocument2 pagesCSE331 - 211 Midterm Question Day PDFAYSHA AKMAL 183-15-11959No ratings yet
- Flow Cytometry, The Next Step in Diagnostic TestingDocument4 pagesFlow Cytometry, The Next Step in Diagnostic Testingtaner_soysurenNo ratings yet
- 053 - Computer GraphicsDocument37 pages053 - Computer GraphicsRejithaVijayachandranNo ratings yet
- Matching AlgorithmDocument3 pagesMatching AlgorithmraghuannamalaiNo ratings yet
- 4 Bit BCD AdderDocument5 pages4 Bit BCD Adderjitendra jhaNo ratings yet
- Chapter 5 - CPU SchedulingDocument41 pagesChapter 5 - CPU Schedulingاس اس100% (1)
- Binary MultiplierDocument14 pagesBinary MultiplierTaruna AggarwalNo ratings yet
- Computer Peripherals & InterfacingDocument128 pagesComputer Peripherals & InterfacingMd MianNo ratings yet
- Assignment C++Document4 pagesAssignment C++Prabhjot ਸਿੰਘ CheemaNo ratings yet
- Assign 2Document1 pageAssign 2Sandhi AgarwalNo ratings yet
- Junior Training Sheet V7.0 - READ Row 34 To Make Your Own EDITABLEDocument39 pagesJunior Training Sheet V7.0 - READ Row 34 To Make Your Own EDITABLEAhmedNo ratings yet
- Operations Research by H A TAHA Solution Manual 8th EditionDocument477 pagesOperations Research by H A TAHA Solution Manual 8th EditionThrs OctNo ratings yet
- CortexM4 FPUDocument14 pagesCortexM4 FPUMohamedAliFerjaniNo ratings yet
- Designing of Alu Using Verilog HDLDocument2 pagesDesigning of Alu Using Verilog HDLPriyanka KumariNo ratings yet
- Rethinking Code GenerationDocument21 pagesRethinking Code GenerationDavidNo ratings yet
- Computer Architecture - A Quantitative Approach Chapter 5 SolutionsDocument14 pagesComputer Architecture - A Quantitative Approach Chapter 5 SolutionsRavi TejaNo ratings yet
- Image Processing Lab ReportDocument11 pagesImage Processing Lab ReportAitzaz HussainNo ratings yet
- LAB 8."binary Multiplier" in FPGADocument2 pagesLAB 8."binary Multiplier" in FPGAMarcoCiauNo ratings yet
- Artificial Neural Networks - IntroductionDocument31 pagesArtificial Neural Networks - IntroductionSofiene GuedriNo ratings yet
- CSC3201 - Compiler Construction (Part II) - Lecture 5 - Code GenerationDocument64 pagesCSC3201 - Compiler Construction (Part II) - Lecture 5 - Code GenerationAhmad AbbaNo ratings yet
- Ocaml Tutorial (Cornell)Document25 pagesOcaml Tutorial (Cornell)Annie FreebiesNo ratings yet
- Wallace Tree Multiplier Part1Document5 pagesWallace Tree Multiplier Part1vineeth_vs_4No ratings yet
- CS 110-Pascal Programming SyllabusDocument2 pagesCS 110-Pascal Programming Syllabuspicefeati100% (1)
- Constraint Satisfaction ProblemDocument9 pagesConstraint Satisfaction ProblemswapsjagNo ratings yet
- Unit 2Document38 pagesUnit 2toshgangwarNo ratings yet
- Crusoe Processor: Seminar Guide: - By: - Prof. H. S. Kulkarni AshishDocument26 pagesCrusoe Processor: Seminar Guide: - By: - Prof. H. S. Kulkarni AshishAshish SinghNo ratings yet
- Masm 2Document16 pagesMasm 2Supraja RamanNo ratings yet
- Matlab Plots in Microsoft WordDocument15 pagesMatlab Plots in Microsoft Wordmtajik2No ratings yet
- Amazon QuestionsDocument2 pagesAmazon QuestionsRajesh ThennanNo ratings yet
- DIP Lecture5Document20 pagesDIP Lecture5Anonymous 0aNRkBg1100% (1)
- EMU8086 TutorialDocument81 pagesEMU8086 TutorialGaurav Arora50% (4)
- Visual Odometry TutorialDocument94 pagesVisual Odometry TutorialMayuresh SarodeNo ratings yet
- Earth Work - PDHDocument38 pagesEarth Work - PDHYahya Ber100% (1)
- Mat Lab PlotsDocument21 pagesMat Lab PlotsBecirspahic AlmirNo ratings yet
- Week05 Graph 1Document69 pagesWeek05 Graph 1Edison Mamani RamirezNo ratings yet
- Introduction To MASMDocument24 pagesIntroduction To MASMGnanasambanthan RajendranNo ratings yet
- Online Analytical ProcessingDocument24 pagesOnline Analytical ProcessingPrachi PatelNo ratings yet
- ('Christos Papadimitriou', 'Midterm 2', ' (Solution) ') Fall 2010 PDFDocument5 pages('Christos Papadimitriou', 'Midterm 2', ' (Solution) ') Fall 2010 PDFJohn SmithNo ratings yet
- Manual of Simulation With Arena For Lab - Note - 3Document16 pagesManual of Simulation With Arena For Lab - Note - 3Kristin MackNo ratings yet
- Aops Community 2017 Amc 8: Colby 25% Alicia 45% Brenda 30%Document5 pagesAops Community 2017 Amc 8: Colby 25% Alicia 45% Brenda 30%Yichi ZhangNo ratings yet
- Applications of Linear AlgebraDocument4 pagesApplications of Linear AlgebraTehmoor AmjadNo ratings yet
- Chapter - 04 Mips Assembly Data PathDocument137 pagesChapter - 04 Mips Assembly Data PathAbubakar sabirNo ratings yet
- Analysis of Digital Images Using Morphlogical OperationsDocument15 pagesAnalysis of Digital Images Using Morphlogical OperationsAnonymous Gl4IRRjzNNo ratings yet
- Morphological Image Processing: OutlineDocument12 pagesMorphological Image Processing: OutlineSarathNo ratings yet
- Robust Face Detection Using The Hausdorff DistanceDocument6 pagesRobust Face Detection Using The Hausdorff DistanceDeepthi SatyanarayanNo ratings yet
- Towards A Robust Face Recognition System Using Compressive SensingDocument4 pagesTowards A Robust Face Recognition System Using Compressive SensinghphuongNo ratings yet
- Log-Linear Models, Extensions, and ApplicationsFrom EverandLog-Linear Models, Extensions, and ApplicationsAleksandr AravkinNo ratings yet
- Stochastic Frontier Analysis and DEADocument3 pagesStochastic Frontier Analysis and DEAHa M ZaNo ratings yet
- Unit 5 - PGP, SmimeDocument43 pagesUnit 5 - PGP, Smimegadidheerajreddy.20.itNo ratings yet
- Activity No. 5 Time Value of Money Interest Rates Future and Present ValueDocument1 pageActivity No. 5 Time Value of Money Interest Rates Future and Present ValueLeslie DelosSantosNo ratings yet
- Mca 504 Data Mining SyllabusDocument2 pagesMca 504 Data Mining Syllabusmanikmathew0% (1)
- Lecture Notes in Earth SciencesDocument267 pagesLecture Notes in Earth SciencesraphaelguiswenyomoNo ratings yet
- 2022 - A CNN Model For Predicting Size of Buried Objects From GPR B-ScansDocument11 pages2022 - A CNN Model For Predicting Size of Buried Objects From GPR B-Scansshiv prasadNo ratings yet
- Problems Solving With Loops:: WHILE DO StatementDocument11 pagesProblems Solving With Loops:: WHILE DO Statementmarwan hazaNo ratings yet
- Two PortDocument13 pagesTwo PortAayushNo ratings yet
- Unctional Ependencies: CS 564-Fall 2020Document39 pagesUnctional Ependencies: CS 564-Fall 2020JadenNo ratings yet
- Volatility: Risk ManagementDocument48 pagesVolatility: Risk ManagementHijabeu CoNo ratings yet
- VLLT@Document9 pagesVLLT@Anonymous UiH9hwNo ratings yet
- Channel Coding NotesDocument15 pagesChannel Coding NotesPramath Keny100% (1)
- Qual 19 p3 SolDocument4 pagesQual 19 p3 SolKarishtain NewtonNo ratings yet
- ALgorithmsDocument73 pagesALgorithmsAbhishek NaikNo ratings yet
- Session 03 - Neural NetworksDocument21 pagesSession 03 - Neural NetworksHGE05No ratings yet
- Slope ApplicationinterpretingDocument8 pagesSlope ApplicationinterpretingAliya AliNo ratings yet
- Measurement Uncertainty PresentationDocument18 pagesMeasurement Uncertainty PresentationStefan KonyanNo ratings yet
- 1.4.2 False-Position Method of Solving A Nonlinear EquationDocument5 pages1.4.2 False-Position Method of Solving A Nonlinear EquationGerardoNo ratings yet
- 03a1 MIT18 - 409F09 - Scribe21Document8 pages03a1 MIT18 - 409F09 - Scribe21Omar Leon IñiguezNo ratings yet
- Week 3 Homework - Fall 2021Document4 pagesWeek 3 Homework - Fall 2021zuhair khanNo ratings yet
- Improved Research Paper - Linear Regression in Market Mix ModellingDocument8 pagesImproved Research Paper - Linear Regression in Market Mix Modellinganshul.courseNo ratings yet
- CS 100 Lab 3 TasksDocument5 pagesCS 100 Lab 3 TasksHassan WaqarNo ratings yet
- Ajms 504 23Document10 pagesAjms 504 23BRNSS Publication Hub InfoNo ratings yet
- On Approximating Complex QuadraticDocument18 pagesOn Approximating Complex Quadraticjiangjinghan008No ratings yet
- A Study On Automatic Speech RecognitionDocument2 pagesA Study On Automatic Speech RecognitionInternational Journal of Innovative Science and Research Technology100% (1)
- LLMS and AiDocument7 pagesLLMS and Ainatnaelsintayehu6127No ratings yet
- 2023 Grade 8 Mathematics Examplar November ExamDocument5 pages2023 Grade 8 Mathematics Examplar November Examselesonthateng0% (1)
- Design and Implementation of Sorting Algorithms Based On FPGADocument4 pagesDesign and Implementation of Sorting Algorithms Based On FPGAeviteNo ratings yet