Kerr Micros

Functional Materials NP 451 December 2014
Kerr microscopy
on a ferrimagnetic garnet
Fabian Lux
Universit Pierre et Marie Curie
M2 Nanomat
Abstract
This laboratory course gives an introduction to the magneto-optical Kerr effect in application to microscopic imaging of magnetic materials. In particular the ferrimagnetic hysteresis of GdPrBi3 (FeAl)5 O12
grown on a Gd3 Ga5 O12 garnet is measured. Besides, the macroscopic Faraday effect is observed.
Contents
I
Introduction
A
The Setup . . . . . . . . . . . . .
B
The Theory . . . . . . . . . . . . .
1
1
1
II Faraday Effect
III Kerr Effect

A
Calibration . . . . . . . . . . . . .
B
Domain width . . . . . . . . . . .
C
Hysteresis . . . . . . . . . . . . .
3
3
5
6
I.
A.
Introduction
The Setup
This laboratory course is divided into two main

parts. The first part focuses on the Faraday effect of the garnet which is a macroscopic effect
that can be observed with the unaided eye.
The second part visualizes the microscopic interpretation of magnetic hysteresis using the
Kerr effect.
Figure 1 shows a schematic drawing of the
experimental setup. A halogen lamp is used as
a light source. It would also be possible to use
a laser, but this will cause a lot of interference
effects and speckle patterns that influence the
image quality, which causes problems in the
illumination of the sample. Nevertheless, the
intensity would be increased a lot. Since the
light dispersion in the garnet may depend on

the wavelength, an interference filter can be
used to select a specific energy corresponding
to = 600 nm. The light beam is focused
in the back focal plane of the objective (focal length fOb = 10 mm, numerical aperture
N A = 0.4), which leads to a uniform illumination of the sample, sometimes referred to as
Khler illumination. A beam splitter makes it
possible to simultaneously collect the reflected
light, focusing it with an ocular (focal length
fOc = 200 mm) on a CCD array. The measured
signal is then send to a computer. Additionally, a coil can be used to apply a magnetic
field (controlled by a LabView program). Ocular and camera can be protected from external
light by a black shield. Also the halogen lamp
is shielded (except the part entering the lense)
to avoid noise in the CCD camera.
B.
The Theory
All physical effects described in this lab come

down to the notion of the permittivity tensor
e( ), which connects the electric displacement
vector D with the electrical field vector E in a
linear manner
D = e0 e( ) E.
(1)
In case of an isotropic medium this tensor is

simply. e( ) = e( ) id. A net magnetization
M will break this isotropy and will lead to a
1
Halogen lamp
Interference filter
l = 600 nm
Aperture diaphragm
Polarizer / Analyzer
Analyzer
BFP
Coil
CCD
Sample holder
Beam splitter
Computer
Figure 1: Schematic drawing of the experimental setup.
tensor of the general form
exx ( )
e = exy (, M )
0
exy (, M )
eyy ( )
0
0
0 .
ezz ( )
As can be derived from Maxwells equations, a

tensor of this form will lead to normal modes
of the propagating light that have circular polarization . And in general, these waves
will experience different complex refractive indices N = n + i . An incident light beam
with linear polarization will therefore experience a rotation of the polarization plane by an
angle
F =
(n+ n )
Im(exy (, M))
2c
2cn
Where the right hand side follows in the limit

of small absorption with n = (n+ + n )/2 and
= (+ + )/2 0. This effect is called
Faraday rotation and will be the object of one
experiment in this lab1
1 As
In principle, the Kerr effect is very similar.

The difference is that the Kerr effect is an effect that occurs at the surface of the material
in reflection. But just like the Faraday effect it
results from the off-diagonal terms in e. However, the effect is much weaker.
II.
Faraday Effect
The first part of this laboratory course investigates the Faraday effect in transmission. To
measure the effect, the light is polarized before the beam splitter and analyzed behind the
sample holder in two configurations. The first
without any sample and the second with transmission through the garnet (for zero and nonzero magnetic field). To obtain some statistics
each of these measurements is repeated three
times. The applied field strength is 100 Oe,
corresponding to a coil current of 2 A as controlled by the LabView program. Due to this
high current, the available time for the experiment is limited.
can be seen from the lecture notes, also a change of ellipticity results.
Figure 2: Image processing for the calibration of the microscope. First, a well focused area is selected. The contrast in
this area is enhanced and a two dimensional Fourier transformation is performed.
Incoming
260 550
260 450
260 550
260 520 60
100 Oe
271 180
271 220
271 500
271 300 170
+100 Oe
251 00
251 50
251 100
251 50 50
ear polarizer together with a Faraday rotator

can block the reflected beam without blocking
the source. Other possible applications concern
for example the magneto-optical read-out of
magnetic recording devices.
Table 1: Measured polarization angles.
This leads to the resulting rotation angles

in degree per garnet thickness (d = 6m).
is assumed to be homogeneous inside the
material. It is important to notice that for zero
applied field 0 Oe no defined polarization angle can be determined with the analyzer.
dL
100 Oe
10 380 180
(1 460 30 )/m
+100 Oe
9 470 80
(1 380 10 )/m
Table 2: Resulting Faraday rotations.
Since this effect is macroscopic it has some

very useful applications. One which is the
Faraday isolator. Handling powerful lasers,
back-reflection of the laser beam can damage
the laser source. Because of the time reversal
breaking in the Faraday effect the polarization
plane of the back-reflected beam can be turned
to an orthogonal position with respect to the
beam that leaves the source. In this way a lin-
III.
A.
Kerr Effect
Calibration
Since the setup is an infinity system the theoretical magnification Mth is given by
Mth =
fOc
= 20.
fOb
(2)
To investigate the period of magnetic domains

on the garnet it is necessary to know the real
magnification. For this purpose, a calibration
sample is inserted to the Kerr microscope. On
the surface of this sample a quadratic array of
dots can be found. The spacing of these dots
its known to be s = 25 m. The spacing of camera pixels is given by the manufacturer and is
dCCD = 6.45 m.
Like every optical microscope, the resolution of the device is limited by the Rayleigh
criterium. The interference filter selects the
3
wave length = 600 nm which leads to a best

possible resolution of
= 0.915 m.
(3)
2N A
In principle the magnification can be increased
(by increasing the focal length of the ocular)
until the Rayleigh criterium makes it pointless
to magnify further. To improve the resolution
and achieve a better magnification, an objective with a larger aperture could be chosen.
For Mth = 20, the spacing of two pixels corresponds to the distance
R = 1.22
6.45
1
m = 0.3225 m R.
(4)
20
3
Therefore, its not useful to increase the magnification.
To determine the real magnification the
Kerr microscope is focused on the calibration
sample. The ambient light is turned off and
the sample is adjusted manually to the focal
point. To improve further, piezoelectric crystals
are used to move the sample. Then the device
is focused on the calibration array described
above. An image of this array is saved with
the computer software. The following procedure of image processing is illustrated in figure
2. First, a well focused area is selected. The
contrast in this area is enhanced by applying
a high pass filter with a certain cutoff. Then,
a two dimensional Fourier transformation is
performed. Fourier amplitudes in x and y directions are shown in figure 3 for the lowest
frequencies.
Both directions show a good agreement.

For further analysis the x direction is used. To
obtain more statistics, higher order frequencies
are also included in the analysis to perform a
linear regression
fn = f n
with the fundamental frequency f .

The
peak positions and their error are determined
with multipeak-Voigt-fitting in IGOR. Figure
4 shows the linear fit to the different order
frequencies with the result
f = (0.0106 0.0001) pixel1 .
Kexp =
Mexp =
(7)
dCCD
Kexp = 24.3 0.3.
pixel
(8)
This value is higher than the expected value of

Mth = 20.
0.8
pixels- 1
Rel. Amplitude
1
pixel
= (3.77 0.04)
f dCCD
m
And the magnification follows from here
c2 / ndf = 0.03
0.06
0.4
(6)
From this the calibration factor K can be calculated by
1.0
0.6
(5)
f = 0.0106
0.0001
0.04
0.02
0.2
0.0
0.00
0.00
0.01
0.02
0.03
0.04
0.05
0.06
pixels-1
Figure 3: Lowest frequency Fourier peaks in x (blue) and

y (orange) direction. Good agreement of the
two directions.
Order
Figure 4: Linear fit to different order frequencies. The

resulting frequency is given in pixel1 .
B.
Domain width
notes). Running the computation for the given

values (error estimation by running p p )
gives
C = 0.21 0.04.
(12)
From this, the saturation magnetization of
MS = 11.14 kA/m and the uniaxial anisotropy
constant Ku = 370J/m3 follows the exchange
constant
Aex =
In this section the domain width (period) of

the garnet and its exchange constant is determined. An interference filter is used. A configuration of polarizer and analyzer gives contrast
to the microscope image, corresponding to the
magnetization of the garnet. The relevant effect
here is the polar Kerr effect (see lecture notes).
It would also be possible to use the ellipticity
to investigate the Kerr effect, but the analyzer
has to be much more sophisticated.
The garnet (on a mirror) is focused in the
Kerr microscope and an image at zero field is
taken. This image is shown in figure 5. The
resulting domain frequency, as obtained from
the FFT in figure 6, is
f = (0.014 0.002) pixel1
(9)
The domain period P can be calculated from

this by applying the calibration factor from the
previous section
P=
1
= (19 3) m
f Kexp
(10)
Which corresponds to a reduced period of

p=
P
d garnet
1
= 3.2 0.5
f Kexp
As demonstrated in the lecture, this quantity is

connected to the domain wall width by
s
Aex
=
= (0.13 0.03)m
(13)
Ku
This is below the Rayleigh resolution of the
microscope and cannot be observed with this
setup. Furthermore, the domain width is much
smaller than the domain width of about 10 m.
The values of domain width and domain wall
width have the typical order which is expected
for magnetic materials.
The characteristic meandering shape of the
magnetic domains can be understood as a process of different energy contributions competing in minimizing the total energy. It costs
energy to create surfaces and if the saturation
magnetization would be so weak that magnetostatic effects could be neglected the characteristic shape that would appear would be spherical
bubbles as magnetic domains, since this minimizes the surface energy.
0.06
0.05
Rel. Amplitude
Figure 5: Magnetic domains in on the garnet. The red

line is the selected plot profile to investigate
the characteristic domain width.
20 MS4 d2 2C
J
= (6.5 2.5) 1012
16Ku
m
0.04
0.03
0.02
0.01
(11)
From this, the characteristic reduced length

C can be computed numerically (see lecture
0.00
0.00
0.01
0.02
0.03
0.04
0.05
pixel-1
Figure 6: FFT of the plot profile in 5
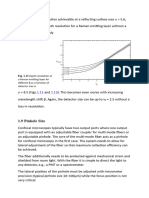
Figure 7: Hysteresis loop for the garnet sample. Total intensity values are calculated by averaging the intensity of each
image.
C.
Hysteresis
In the last part a hysteresis loop of the garnet is observed with the Kerr microscope. A
LabView program controls to coil current and
triggers the CCD camera to take images at specific stages of the applied magnetic field, which
is varied between 100 Oe and +100 Oe. To
obtain the hysteresis curve, the intensity is averaged for each each recorded image. The average intensity decodes the total magnetization
of the sample. It is therefore no surprise, that
the recorded curve as shown in figure 7 is similar to the one recorded by a SQUID device.
Also, figure 7 shows the associated images as
obtained by the CCD camera. This gives a microscopic interpretation of the hysteresis loop.
In the process of decreasing the absolute
field the system stays remanent up to a certain point. At this critical field, domains with
opposite magnetization appear (often pinned

at defects). From these centers the domains
start to increase their size. At zero field an
equilibrium of up and down magnetization is
achieved. Would the temperature influence be
minimized by cooling the sample, the apparent jump would occur closer to the point of
zero field. In this case only the pinning will
influence the shape.
In the process of increasing field their is a
more continuous transition to saturation. No
jump appears since the domains can increase
continuously. The domains pinned to defects
can resist longer and disappear the last. The
curve is more smooth.
This lab showed how a simple optical setup
can be used to visualize magnetic domains. It
even shows a way to determine the domain
wall width without being able to resolve the
width in the microscopic image.
1.0
0.8
0.6
0.4
0.2
0.0
Amplitude
0.6
0.4
0.2
0.0
0
0.6
0.4
0.2
0.0
1
2
20
40
60
Frequency [1/pixel]
5
-3
80x10
Figure 8: Multipeakfitting in IGOR.

Kerr Micros

Uploaded by

Copyright:

Available Formats

Kerr Micros

Uploaded by

Document Information

Original Title

Copyright

Available Formats

Share this document

Share or Embed Document

Sharing Options

Did you find this document useful?

Is this content inappropriate?

Copyright:

Available Formats

Kerr Micros

Uploaded by

Copyright:

Available Formats

Functional Materials NP 451 December 2014

III Kerr Effect

This laboratory course is divided into two main

light dispersion in the garnet may depend on

All physical effects described in this lab come

In case of an isotropic medium this tensor is

Functional Materials NP 451 December 2014

Figure 1: Schematic drawing of the experimental setup.

tensor of the general form

As can be derived from Maxwells equations, a

Where the right hand side follows in the limit

In principle, the Kerr effect is very similar.

Functional Materials NP 451 December 2014

ear polarizer together with a Faraday rotator

Table 1: Measured polarization angles.

This leads to the resulting rotation angles

Table 2: Resulting Faraday rotations.

Since this effect is macroscopic it has some

To investigate the period of magnetic domains

Functional Materials NP 451 December 2014

wave length = 600 nm which leads to a best

Both directions show a good agreement.

with the fundamental frequency f .

This value is higher than the expected value of

And the magnification follows from here

From this the calibration factor K can be calculated by

Figure 3: Lowest frequency Fourier peaks in x (blue) and

Figure 4: Linear fit to different order frequencies. The

Functional Materials NP 451 December 2014

notes). Running the computation for the given

In this section the domain width (period) of

The domain period P can be calculated from

Which corresponds to a reduced period of

As demonstrated in the lecture, this quantity is

Figure 5: Magnetic domains in on the garnet. The red

From this, the characteristic reduced length

Figure 6: FFT of the plot profile in 5

Functional Materials NP 451 December 2014

opposite magnetization appear (often pinned

Functional Materials NP 451 December 2014

Figure 8: Multipeakfitting in IGOR.

You might also like