Chapter 8: Field Effect Transistors: A. Introduction To Fets
Chapter 8: Field Effect Transistors: A. Introduction To Fets
Uploaded by
BmanCopyright:
Available Formats
Chapter 8: Field Effect Transistors: A. Introduction To Fets
Chapter 8: Field Effect Transistors: A. Introduction To Fets
Uploaded by
BmanOriginal Description:
Original Title
Copyright
Available Formats
Share this document
Did you find this document useful?
Is this content inappropriate?
Copyright:
Available Formats
Chapter 8: Field Effect Transistors: A. Introduction To Fets
Chapter 8: Field Effect Transistors: A. Introduction To Fets
Uploaded by
BmanCopyright:
Available Formats
Chapter 8: Transistors, part 3
Chapter 8: Field Effect Transistors
Transistors are different from the basic electronic elements in that they have three
terminals. Consequently, we need more parameters to describe their behavior than one
simple current-voltage characteristic. We found that thinking of the transistor as a
current amplifier was a particularly useful model. This model, however, does have its
limitations and we could extend it.
A next step would be a transconductance model, such the Ebers-Moll model. In this
improved model, the collector current depends on the base-emitter voltage, so that VBE
produces IC. In this model, VBE also produces IB so this model includes the earlier current
amplifier model in addition to the new features.
I. Field-Effect Transistors
A. Introduction to FETs
This weeks we introduce a new element
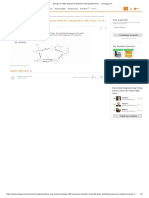
D
D
called a Field-Effect Transistor (FET). It is also a
three-terminal element. The three terminals are
similar to the transistors base, emitter and
collector, but they are called the gate, source and
G
G
drain. The initial FETs we will use (the 2N5485)
have identical packages to the transistors we used
S
S
in earlier in the semester. The schematic symbol
for the FETs we will use are shown in figure 8.1 Figure 8.1: An n-channel JFET
on the right.
(left) and a p-channel JFET (right).
A FET is produced from a single piece of
conducting silicon that connects to the source and the drain. This is called the channel.
The gate is then created by diffusing a third connection, the gate. A voltage applied to the
gate controls the conductivity of the channel.
The gate-channel junction looks like a diode that never conducts hence the gate draws
no current. This is the major difference between normal transistors and FETs.
Consequently FETs have extremely large gate input impedances (>1012). Thus, we will
be forced from the start into modeling the device with a transconductance model where
the drain current depends on the gate voltage and not the current. This is the major
difference between the bipolar diodes that we used previously and FETs.
FETs are extremely important as input stages to amplifiers. Since they have such a
large input impedances that they almost attain the ideal of measuring a voltage without
drawing any current from the source. This is great if you want to measure small charges
deposited on capacitors as you might want to do in a particle detector.
- 65 -
Chapter 8: Transistors, part 3
FETs come in five general types, but we will restrict ourselves to JFETs (for Junction
FET) initially and our examples will only use n-channel JFETs. These have n channel
doping and are similar to npn transistors. The p channel JFET requires the opposite
voltage on the gate. They usually have poorer performance due to the lower mobility and
shorter lifetimes of holes, as compared to electrons.
As mentioned above, the source-drain current is the only current that flows through a
FET. The source-drain current is labeled ID. The voltage applied to the gate terminal
enables this current by creating an electric field inside the channel. There is no
fundamental difference between the source and drain terminals of a JFET. The gate-drain
capacitance, however, is usually lower than the gate-source capacitance so they are
usually used as specified. This makes it different from a normal transistor, since current
can flow either from the drain to the source or from the source to the drain.
Note that there is a maximum value and a minimum value for the gate voltage in
order to keep the device operating. Since a JFET has a diode junction separating the gate
from the channel, the gate must be held at a voltage of less than 0.6 V above the channel
(usually the source terminal). If the gate voltage becomes greater than this, the junction
will become conducting and the gate current will no longer be zero. Usually, we will not
let the voltage between the gate and the source (VGS) get any greater than 0. If the gate is
biased too negative then no current flows and the channel is said to be pinched off.
This minimum gate voltage, called VP, is a characteristic that varies from one model of
JFET to the next. It is usually in the range from 3 V to 10 V. Even within the same
type of FET this parameter varies
significantly from one device to the next.
For example, the range specified for a
2N5485 the range is between -0.3 V and -3.0
V.
Lets summarize these properties:
For VGS < Vp:
ID = 0
ID
(8.1)
For VGS > 0.6 V: Device Fails! (8.2)
When VGS is between these bounds ID
depends on both VGS and VDS. A complete
description of the device would require a
two-dimensional plot showing how ID varies
with both VGS and VDS.
VDS
Figure 8.2: A sketch of drain current
versus channel voltage.
B. Regions of Operation
For a fixed VGS, the basic behavior of the drain current as a function of the channel
voltage is shown in Figure 8.2 above. The behavior can be simply modeled in two
regions. For small values of VDS, ID is almost proportional to VDS just like a resistor. This
is called the linear region. For reasonably large values of VDS, ID has little dependence
on VDS. This is called the saturation region. The actual relationships and conditions can
be approximated as:
- 66 -
Chapter 8: Transistors, part 3
For VDS < VGS VP:
ID = k [2(VGS VP)VDS - V2DS]
Linear Region
For VDS > VGS VP:
ID = k (VGS VP)2
Saturation Region (8.4)
(8.3)
For small enough voltages the quadratic term is small. In this case, the current in the
linear region is proportional to VDS just like a resistor. This is true even for negative VDS.
Since ID is proportional to both VGS and VGS this gives us a way to make voltagecontrolled resistors. Moreover, since ID is proportional to both VDS and VGS, we can
generate a current corresponding to the product of two signals.
In the saturated region ID is nearly independent of VDS. We can use this to make
excellent currents sources and source followers. This is similar to our transistor-based
emitter follower but with a much larger input impedance. Note that in this region there is
still a small slope and this slope increases for larger gate voltages. We will discuss the
saturated region later in the chapter.
C. A Voltage Controlled Resistor
From Equation 8.3 we can see that
the drain current is proportional to VDS,
when VDS is small, and the
proportionality constant is proportional to
VGS.
This is perfect for a making
voltage-controlled resistor. A typical
data sheet will list RD(ON) as the resistance
measured when the gate is shorted to the
source. From Equation 8.3 we see that
RD(ON) is approximately -1/2kVp. If you
put this resistor in series with a fixed
resistor, then you will have a voltagecontrolled attenuator. If this follows or
precedes an amplifier the combination
would be an amplifier with a voltagecontrolled gain.
VIN
RD
-15 V
VOUT
10k
RG
VIN
Figure 8.3: Uncompensated voltage-divider.
RD
VOUT
The resistor RD and the FET in
Figure 8.3 form a voltage divider to
attenuate the input voltage. The size of
the equivalent resistance of the FET is
determined by VGS, which is set by the
potentiometer.
-15 V
By making the right choice of gate
voltages we can improve the circuit by
eliminating the quadratic term in
Equation 8.3 and thus improving the
linearity of the attenuator.
From
Equation 8.3 we see that
Figure 8.4: Compensated voltage-divider.
1/RDS = ID / VDS
- 67 -
Chapter 8: Transistors, part 3
= k [2(VGS VP) - VDS]
(8.5)
If we set VGS to exactly VDS/2 then we find
RDS = -1/(2kVP)
(8.6)
Figure 4 shows a version of the attenuator that employs this improved linearity. The two
resistors connected to the gate force half of the drain voltage onto the gate. They should
be much larger than the potentiometer. The capacitor just blocks DC so that only the
signal part of the input voltage is fed to the gate.
Application: Amplitude Modulator
If you feed a second, lower frequency, signal into the gate in addition to the DC
voltage from the potentiometer, then you can modulate the attenuation of your voltage
divider. Of course, you should feed this in via a capacitor so that you do not disturb the
quiescent (DC) conditions.
II. The Saturated Region
As we saw in equation 4, for large values of VDS the drain current only depends on
VGS :
ID = k (VGS VP)2.
(8.7)
This saturation is useful, for example, for making current sources and followers. As
discussed earlier, there is still some dependence of ID on VDS even in the saturated region.
You can, however, reduce this effect with a few extra tricks.
A. Transconductance
The transconductance of a FET is denoted by gm and is defined as
(8.8)
gm = ID/VGS
gm 2k (VGS VP)
(8.9)
1/2
gm = 2(kID)
(8.10)
The transconductance will be useful in understanding the behavior of the FET amplifiers.
You can interpret it as the slope of ID vs VGS in the saturated region and depends on
your choice of ID. A curve of gm(VGS) and gm(ID) are usually shown in the data sheets and
they have complicated shapes. If you know the value for one set of conditions you can
use the above relationships to scale to other similar values.
The transconductance has units of -1 which is known as a mho (pronounced moe).
You often seed the units of mho (or umho pronounced micro-moe) for 10-6 mho and
mmho (milli-moe) for 10-3 mho in FET specifications. You might also see an inverted
capital omega or S to represent this unit.
The remainder of this section will cover some applications for FETs employing the
saturated region.
- 68 -
Chapter 8: Transistors, part 3
B. JFET Current Sources
You can easily make a FET current source simply by connecting the gate to the
source (i.e. VGS = 0 V) and applying a high enough voltage to the drain that the JFET
operates in the saturated region (Figure 1). This generates a current through the load. This
specific current is IDSS, where the subscript denotes that this is the drain current when the
gate is shorted to the source.
According to the transconductance model given by equations 3 and 4, the saturation
current, IDSS, when VGS = 0, is given by
IDSS = kVP2
(8.11)
Two-terminal JFETs, such as the 1N5294, are exactly this
circuit packaged to look like a diode and sold under the
name current-regulator diodes.
Since we know there are large variations in VP this
may not seem like the best specified device. In fact, when
marketing these devices, a manufacturer will actually
measure its response and only sell devices under this
product type when they pass the roughly specified current
(within a factor of two of 7 mA). This is called
preselection and is common in some categories of
commercial electronics production and also in devices
with large variations such as photodetectors. Since this is
expensive, the companies invest huge amounts into
development on the more expensive components (e.g.
CPU chips or disk drive heads) to improve quality control
during fabrication.
+V
RL
RS
You can make this circuit an adjustable or Figure 8.5: A programmable
programmable constant current source by adding a constant current source
resistor between the gate and source to provide an offset driving a load.
(Figure 5). Since there is a voltage drop across the
resistor the current is given by
I D = k (VGS V P )
= k ( RS I D V P )
(8.12)
R I
= I DSS S D + 1
VP
This can be solved for ID but it is rather ugly. In practice, one normally starts from a plot
of ID vs VGS on the devices data sheet to get a rough idea of the source resistor. Since the
saturation properties are not well determined in the fabrication process (up to factors of
10), use a potentiometer if you wish to sink a specific current.
- 69 -
Chapter 8: Transistors, part 3
C. JFET Follower
The drain current in a JFET operating in the saturation region depends only on VGS.
Because of this, you can add a source resistor to a FET to provide at type of negative
feedback. This is called a source follower.
In the followers quiescent state there will be nominal
values for ID and VGS. An increase in the gate voltage will
increase the current into the source resistor. This will cause
an increased voltage drop and act to raise the source voltage.
It is conventional to use lower case letters to represent small
variations from the quiescent point.
+VDD
VIN
VOUT
In our transconductance model, small variations would be
governed by
RS
id = gm(vg - vs).
(8.13)
The source voltage is tied to the drop across the source
resistor,
vs = idRS.
Solving these two equations, we find that
vs =
(8.14)
RS g m
RS
vg =
vg
1 + RS g m
1 g m + RS
Figure 8.6: A simple source
follower.
(8.15)
For RS much greater than 1/gm we see that vg vs (i.e. gain = 1) and therefore this is a
follower.
FET follower limitations
From Equation 9, we can see that the source follower acts like a voltage divider with
the FET behaving like a resistor of 1/gm. Since it is a voltage divider we can determine
its output impedance. Since the FET is the smaller resistor in the divider (or the output
will not be very close to the gate), the output impedance of the source follower is just
1/gm, which is typically a few hundred ohms at currents of a few milliamps.
So, our simple follower, however, does not behave too well:
1. As VGS varies, the nonlinear transconductance will distort the input.
2. It has quiescent output voltage that is specified by the pinch of voltage of the
device and hence is unpredictable.
3. The required VGS to produce a given quiescent current varies a lot from one
device to the next
4. The output impedance is relatively high.
On the good side, the input impedance is immense.
- 70 -
Chapter 8: Transistors, part 3
A matched pair follower
A very common solution is to replace the ground at the end of the source resistor with
a current source. This is called and active load. By putting in a constant current sink, we
always have the same ID and thus a fixed value for VGS. The first problem is solved. It
does not, however, fix the other problems.
We can do an even better job by noting
manufacturing variations in FETs are significantly
smaller for FETs made from the same piece of silicon
wafer, or die. You can think of them as identical twins
instead of just siblings. This is called a matched pair.
The 2N3958 and U441 are examples of a matched pair
JFETs.
Using the second JFET as the active load gets rid of
most of the problems in the FET follower (Figure 7).
The second JFET keeps the current constant, fixes VGS,
and eliminates the nonlinearities. The matched resistors
also add better ID predictability. Furthermore, when you
use a matched FET pair and symmetric power supplies
it largely eliminates the DC offset at the output. To fix
the poor output impedance, one would need to add an
op amp follower or amplifier to the output.
Matched pairs are used for the input stages of most
charge measurement applications (e.g. oscilloscope
inputs), sensitive electrometers, measurement of small
charges (e.g. fC) like one sees in particle detectors, and
current pre-amplifiers for photo-detectors.
+10 V
VIN
RS
VOUT
RS
-10 V
Figure 8.7: A matched pair
follower.
Design Exercises
Design Exercise 8-1: Design a programmable current source with a design current of
1mA and a variable gate-source resistor. Pick a reasonable value based on the plot of ID
as a function of VGS from the datasheet of a 2N5485.
Design Exercise 8-2: Determine the quiescent voltages (i.e. VGS, VS, and VDD) and the
quiescent power consumption for a source follower with IDS(quiescent) = 1 mA and RS =
4.7 k. The N-JFET for the circuit has the following properties: VP = -2 V, IDSS = 3 mA,
and gm = 2.5 mmhos.
(hint: Start by assuming that the circuit is operating in the saturation region and then
choose VDD at the end of the calculation to ensure that the FET is well into the saturation
region.)
- 71 -
Chapter 8: Transistors, part 3
- 72 -
Chapter 8: Transistors, part 3
Lab 8: Introduction to FETs
1. N-JFET Basics (1.5 hours)
a) Measure the characteristics of a 2N5485 n-channel JFET by
measuring ID versus VDS while the gate is tied to the source (i.e.
VGS = 0). Construct a sketch as you make your measurements.
Using the Formulas 1 and 2 from the text and data in the linear
and saturated regions, compute VP and k.
b) Measure the characteristics of the JFET by measuring ID
versus VDS for an additional value of VGS between VP and
ground. Does this agree with our model (i.e. does one value of
k fit all your data)?
V+
A
V- or GND
Do lab exercise 2 or 3.
2. Voltage controlled JFET attenuators (1.5 hours)
a) Construct an uncompensated attenuator with RD = 10 K. Use a voltage divider
with your variable 15 V supply to generate the VGS control voltage in the
approximate range of -0.5 V to -5 V. Connect the output of the voltage divider to the
gate through a 1 M gate resistor. Try to attenuate your input by a factor of 10 using
this device when you drive the drain with a small signal (<1 V) around 1 kHz. Note
that this attenuator even works for the negative values of VDS function generator.
Check for distortion using the FFT feature on the oscilloscope.
b) Now compensate your attenuator using a second 1 M feedback resistor between
the drain and the gate. Use a ~0.1 F capacitor to block the DC drain voltage.
Measure the new attenuation and distortion. How do the new characteristics compare
to the uncompensated ones?
c) Connect the signal from another function generator to the voltage divider to form a
bias-T using another capacitor. Set this frequency to be roughly 10 times lower than
the frequency on the drain. Use small AC inputs for both signals (tenths of volts) and
describe the output. Describe the signal in the time domain and in frequency space.
Do your results agree with theory? What arithmetic operation does your circuit
implement on the two input signals?
- 73 -
Chapter 8: Transistors, part 3
3. Matched-pair source-follower (1.5 hours)
a) Construct a simple source follower with a 2N3958 (or U441) JFET. Use a 4.7 k
source resistor. Using a small sine wave around 1 kHz, measure its gain and DC
offset. Estimate gm from the attenuation. Measure its output impedance. Do they
agree?
b) Add an active load to your source follower using the second JFET from the
matched pair. Measure its new gain, its DC offset and its output impedance.
+10 V
VIN
RS
VOUT
RS
-10 V
A matched-pair follower
- 74 -
You might also like
- Scientech 2266Document33 pagesScientech 2266sarikapravinNo ratings yet
- Characteristics of FETDocument8 pagesCharacteristics of FETYogesh Kumar100% (1)
- Snubber Circuit - Theory, Design and ApplicationDocument18 pagesSnubber Circuit - Theory, Design and ApplicationUtpal100% (10)
- Peças Pá Carregadeira Ensign YX636Document221 pagesPeças Pá Carregadeira Ensign YX636Luiz Gustavo Duarte100% (1)
- Chapter 4 - JFET PDFDocument13 pagesChapter 4 - JFET PDFnelsonjnelsonjNo ratings yet
- JFET CharacteristicsDocument9 pagesJFET CharacteristicsAasiq Mohamed100% (1)
- 4 Zener Voltage Regulator Diode Clippers ClampersDocument7 pages4 Zener Voltage Regulator Diode Clippers ClampersmakreloadedNo ratings yet
- Basic Triac-SCR Projects Circuits TutorialDocument7 pagesBasic Triac-SCR Projects Circuits TutorialAmmar YasserNo ratings yet
- Unit 5 Voltage RegulatorDocument20 pagesUnit 5 Voltage RegulatorSadrina MahamudNo ratings yet
- JFET Characteristics PDFDocument9 pagesJFET Characteristics PDFSougata GhoshNo ratings yet
- RelaysDocument4 pagesRelaysSathya AyhtasNo ratings yet
- Bending Loss Experiment in Optical FiberDocument3 pagesBending Loss Experiment in Optical Fiber3176RACHANA CHOUGULE100% (1)
- Pulses in Cables: ReferencesDocument5 pagesPulses in Cables: ReferencesPaul DumitruNo ratings yet
- Lecture 20 Boundary Conditions IDocument14 pagesLecture 20 Boundary Conditions IZuha FatimaNo ratings yet
- Optical ManualDocument26 pagesOptical ManualsharonfranklinNo ratings yet
- BJT SummaryDocument4 pagesBJT SummaryPatricia Rossellinni Guinto100% (1)
- Skin Effect and Dielectric Loss Models of Power Cables 04784562Document8 pagesSkin Effect and Dielectric Loss Models of Power Cables 04784562Gilberto Mejía100% (1)
- PART IV. Instrument TransformersDocument30 pagesPART IV. Instrument TransformersuplbselesNo ratings yet
- Laboratory Manual For Ac Electrical CircuitsDocument75 pagesLaboratory Manual For Ac Electrical CircuitsArnulfo LavaresNo ratings yet
- Wireless FM Microphone CircuitDocument2 pagesWireless FM Microphone Circuitcuongspvl2713No ratings yet
- Calibration of Voltmeter and AmmeterDocument57 pagesCalibration of Voltmeter and AmmeterMs.Ezhilarasi ICE DepartmentNo ratings yet
- Network SynthesisDocument12 pagesNetwork SynthesisHarshit GargNo ratings yet
- Voltage Multipliers: Half-Wave Voltage DoublerDocument5 pagesVoltage Multipliers: Half-Wave Voltage DoublerKade Ben100% (1)
- Sedra/Smith Microelectronic Circuits 6/E Chapter 3: Diodes: S. C. Lin, EE National Chin-Yi University of TechnologyDocument65 pagesSedra/Smith Microelectronic Circuits 6/E Chapter 3: Diodes: S. C. Lin, EE National Chin-Yi University of TechnologyRAIHAN AZWAR IBRAHIM PULUNGANNo ratings yet
- Unit-1 Semiconductor Diodes PDFDocument103 pagesUnit-1 Semiconductor Diodes PDFRajarao MandaNo ratings yet
- LC CircuitDocument15 pagesLC CircuitKing SharmaNo ratings yet
- Operational AmplifierDocument24 pagesOperational AmplifierSead ArifagićNo ratings yet
- Three-Phase Power CircuitsDocument24 pagesThree-Phase Power Circuitshodeegits9526100% (1)
- Geiger M Uller Counter (GM Counter)Document26 pagesGeiger M Uller Counter (GM Counter)AviteshNo ratings yet
- Permeability (Electromagnetism)Document6 pagesPermeability (Electromagnetism)blerb795No ratings yet
- Experiment No. 13: Objective: To Investigate The Use of JFET As A Constant Current Source & As Chopper ApparatusDocument3 pagesExperiment No. 13: Objective: To Investigate The Use of JFET As A Constant Current Source & As Chopper ApparatusUsama SagharNo ratings yet
- Edc NotesDocument4 pagesEdc Notesmeeravali_snNo ratings yet
- Experiment Photocell6572Document6 pagesExperiment Photocell6572ShubhamNo ratings yet
- Bootstrap Time Base GeneratorDocument2 pagesBootstrap Time Base GeneratorFarheenNo ratings yet
- Ballistic GalvanometerDocument14 pagesBallistic GalvanometerPhysics Instruments100% (1)
- Study of Gamma Energy Spectrum Using A Scintillation Counter With Single Chanel AnalyzerDocument10 pagesStudy of Gamma Energy Spectrum Using A Scintillation Counter With Single Chanel AnalyzerHelpUnlimitedNo ratings yet
- Electric Machine ch03Document16 pagesElectric Machine ch03api-302761543No ratings yet
- Electric CurrentDocument9 pagesElectric CurrentmerryNo ratings yet
- AWP NotesDocument451 pagesAWP Noteskomar33No ratings yet
- ECE101 Modules 9 Zener DiodesDocument34 pagesECE101 Modules 9 Zener DiodesGio AscanNo ratings yet
- Load and Line RegulationDocument11 pagesLoad and Line RegulationHelpUnlimited0% (1)
- EENG223 Lec04 CircuitTheorems PDFDocument71 pagesEENG223 Lec04 CircuitTheorems PDFSmit Shine100% (2)
- Bipolar Transistors FundamentalsDocument42 pagesBipolar Transistors FundamentalsHemal VyasNo ratings yet
- Section 2 Three Phase Power FundamentalsDocument112 pagesSection 2 Three Phase Power FundamentalsAhmedNo ratings yet
- Active & PassiveDocument3 pagesActive & Passivevirendra.aryaNo ratings yet
- Magnetic Polarity Detector Circuit Using Hall Effect SensorDocument11 pagesMagnetic Polarity Detector Circuit Using Hall Effect SensorKoushik MaityNo ratings yet
- Transmission Lines NotesDocument9 pagesTransmission Lines NotesAshutosh Daichang GautamNo ratings yet
- Impedance of RL Circuits: Series RL Circuits: Experiment No. 2Document16 pagesImpedance of RL Circuits: Series RL Circuits: Experiment No. 2NicoNo ratings yet
- EE5251 Unit 1Document129 pagesEE5251 Unit 1Sathya100% (1)
- Characteristics of Diodes, BJT, MOSFETDocument11 pagesCharacteristics of Diodes, BJT, MOSFETvamsiprasannakoduru100% (2)
- Chapter 5 MOSFET Theory and ApplicationsDocument28 pagesChapter 5 MOSFET Theory and ApplicationsanjugaduNo ratings yet
- Fourier Series Problems and SolutionDocument78 pagesFourier Series Problems and SolutionGellie Buenaventura100% (2)
- Energy Levels of Semiconductor, Conductors and InsulatorsDocument53 pagesEnergy Levels of Semiconductor, Conductors and InsulatorsTawki BakiNo ratings yet
- Galvanometer's Conversion To Ammeter and VoltmeterDocument1 pageGalvanometer's Conversion To Ammeter and Voltmeteranshvishwakarma2005No ratings yet
- Optical and Microwave Technologies for Telecommunication NetworksFrom EverandOptical and Microwave Technologies for Telecommunication NetworksNo ratings yet
- Lsk489 Guide to Fets for Voltage Controlled CircuitsDocument10 pagesLsk489 Guide to Fets for Voltage Controlled Circuitsanalogio codeNo ratings yet
- p89v51 SemiDocument3 pagesp89v51 SemiBmanNo ratings yet
- MT7623N Public Datasheet For Development Board v1.1 PDFDocument1,305 pagesMT7623N Public Datasheet For Development Board v1.1 PDFBmanNo ratings yet
- Edison 5Document73 pagesEdison 5sabot123No ratings yet
- 99s ClockDocument1 page99s ClockBmanNo ratings yet
- Booksorber ManualDocument34 pagesBooksorber ManualBmanNo ratings yet
- 8086 ProgramsDocument61 pages8086 ProgramsBmanNo ratings yet
- ECEsyllabus 2013Document139 pagesECEsyllabus 2013BmanNo ratings yet
- 101i-Super C Hydraulic Saw ManualDocument68 pages101i-Super C Hydraulic Saw Manualgeorge israelNo ratings yet
- QJC Catalogue (2024-10-07 05 - 21 - 13)Document88 pagesQJC Catalogue (2024-10-07 05 - 21 - 13)jesus perezNo ratings yet
- Blue Ocean StrategyDocument26 pagesBlue Ocean StrategyDanya ShahidNo ratings yet
- Mixed Use & Hybrid Buildings: Why They're Better For Our CitiesDocument6 pagesMixed Use & Hybrid Buildings: Why They're Better For Our CitiesRachel Johnson100% (1)
- TNB MvabcDocument11 pagesTNB Mvabcpelarocha100% (2)
- Hospital Websites EvaluationDocument19 pagesHospital Websites EvaluationBarryNo ratings yet
- PR PiperJ3Cub A4Document28 pagesPR PiperJ3Cub A4marcial rubioNo ratings yet
- Commax Dp-La101 (En)Document10 pagesCommax Dp-La101 (En)gigioneumaticaNo ratings yet
- 45ps PhaseDocument2 pages45ps PhasearifNo ratings yet
- Mainline PPR LT.21.DDocument1 pageMainline PPR LT.21.DVictor AfandiNo ratings yet
- Optiplex 9020 Desktop Owner's Manual en UsDocument59 pagesOptiplex 9020 Desktop Owner's Manual en Usjay0154No ratings yet
- Purchase Order Approved PermitDocument1 pagePurchase Order Approved Permitkebede7075No ratings yet
- 8-Project Management MaturityDocument14 pages8-Project Management MaturityHassan ParvezNo ratings yet
- CP500 UserDocument338 pagesCP500 UserFlorin NeacsuNo ratings yet
- Nit CR 2024Document51 pagesNit CR 2024manikian27No ratings yet
- Capability Maturity Model IntegrationDocument13 pagesCapability Maturity Model IntegrationFaisca_RNo ratings yet
- Ac Induction Motor Data Sheet: General Specification Performance DataDocument2 pagesAc Induction Motor Data Sheet: General Specification Performance DataArjun SomaiyaNo ratings yet
- Weller CatalogDocument97 pagesWeller CatalogИлья ХинкинNo ratings yet
- Speaker Lab ReportDocument2 pagesSpeaker Lab Reportapi-456993701No ratings yet
- GE Additive - EBM - White Paper - FINALDocument10 pagesGE Additive - EBM - White Paper - FINALSebastian ParedesNo ratings yet
- PRL Internship ReportDocument15 pagesPRL Internship ReportJairo CortesNo ratings yet
- CERT-Appearance-Gingoog CityDocument1 pageCERT-Appearance-Gingoog CityEnforcement DivisionNo ratings yet
- Product Range Slide Bearings and CouplingsDocument4 pagesProduct Range Slide Bearings and CouplingsAli HashemiNo ratings yet
- Claret School of City: ZamboangaDocument2 pagesClaret School of City: ZamboangaJasmine Delasas100% (1)
- 27002-Splunk Guide For ISODocument6 pages27002-Splunk Guide For ISOGDJhonesNo ratings yet
- UT Tyler Teacher Directed Lesson Plan FormatDocument5 pagesUT Tyler Teacher Directed Lesson Plan Formatapi-401527683No ratings yet
- Question: Design A "100" Sequence Detector Using Below Ip Ops. On DDocument3 pagesQuestion: Design A "100" Sequence Detector Using Below Ip Ops. On DAbood AtiyatNo ratings yet
- Protective Relay - Wikipedia, The Free EncyclopediaDocument9 pagesProtective Relay - Wikipedia, The Free Encyclopediaamaresh27071965No ratings yet
- Inbound and Outbound Idoc ConfigurationDocument13 pagesInbound and Outbound Idoc Configurationamitava_bapiNo ratings yet