Math 30-1: Polynomial, Radical, and Rational Functions

PRACTICE EXAM

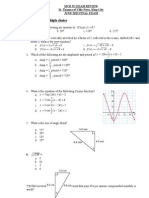
1. A zero of the polynomial function P(x) = x2 - 4x - 5 is:

A. -2
B. -1
C. 0
D. 1

2. Given the graph of P(x) = (x + 1)2(x - 2), the zeros and their multiplicities are:

A. -2 (multiplicity = 1); -1 (multiplicity = 1); 2 (multiplicity = 1)

B. -1 (multiplicity = 1); 2 (multiplicity = 2)
C. -1 (multiplicity = 2); 2 (multiplicity = 1)
D. 0 (multiplicity = -2)

3. The y-intercept of P(x) = 1 (x - 5)(x + 3) is found at the point:

2
A.

B.

C. (0, -3)
D. (0, 5)

4. The graph of P(x) = -x2(x + 1):

A. Trends upwards linearly from Quadrant III to Quadrant I.

B. Trends parabolically from Quadrant II to Quadrant I.
C. Trends downwards linearly from Quadrant II to Quadrant IV.
D. Trends parabolically from Quadrant III to Quadrant IV.

Polynomial, Radical, and Rational Functions Practice Exam www.math30.ca

5. The polynomial function P(x) = x(4x - 3)(3x + 2) has zeros of:

A. -2, 0, 3

B.

C.

D.

6. The polynomial function corresponding to the graph is:

A.

B.
(2, -6)

C.

D.

7. The polynomial function that matches the given Characteristics of P(x)

characteristics of P(x) is: x-intercepts: (-1, 0) and (3, 0)
sign of leading coefficient: (+)
A. polynomial degree: 4
relative maximum at (1, 8)
B.

C.

D.

8. A box with no lid can be made by cutting out squares x

from each corner of a rectangular piece of cardboard
x
and folding up the sides. A particular piece of cardboard
has a length of 20 cm and a width of 16 cm. The side
16 cm
length of a corner square is x.
The volume function and its domain are:

A. V(x) = x(20 - x)(16 - x); Domain: {x | 0 < x ≤ 4, x ε R} 20 cm

B. V(x) = x(20 - x)(16 - x); Domain: (0, 4)
C. V(x) = x(20 - 2x)(16 - 2x); Domain: (0, 8)
D. V(x) = x(20 - 2x)(16 - 2x); Domain: {x | 0 ≤ x ≤ 8, x ε R}

www.math30.ca Polynomial, Radical, and Rational Functions Practice Exam

9. A cylinder with a radius of r and a height of h is inscribed within a sphere r h
that has a radius of 4 units. The polynomial function, V(h), that 2
expresses the volume of the cylinder as a function of its height is:

A. h
4
B.

C.

D.

Partially completed long division.

10. A partially completed polynomial division is shown.
The next step in the long division process is to: x2
x+2 x3 + 2x2 - 5x - 6
A. Add 5 in the quotient. - x3 + 2x2
B. Subtract 5 in the quotient.
- 5x - 6
C. Add 5x in the quotient.
D. Subtract 5x in the quotient.

P(x) R
11. (x3 - 1) ÷ (x + 2), expressed in the form = Q(x) + , is:
D(x) D(x)
A.

B.

C.

D.

12. The correct synthetic division of (3x3 - x - 3) ÷ (x - 1) is:

A. -1 3 0 -1 -3 B. -1 3 -1 -3
+ -3 3 -2 - -3 -2
3 -3 2 -5 3 2 -1

C. -1 3 0 -1 -3 D. 1 3 0 -1 -3
- -3 -3 -2 - 3 -3 2
3 3 2 -1 3 -3 2 -5

Polynomial, Radical, and Rational Functions Practice Exam www.math30.ca

13. A rectangular prism has a volume of x3 + 6x2 - 7x - 60. If the
V = x3 + 6x2 - 7x - 60
height of the prism is x + 4, the dimensions of the base are:

A. (x + 5) and (x - 3)
B. (x - 5) and (x - 4) x+4
C. (x - 1) and (x + 1)
D. (x + 2) and (x + 3)

14. When 2x3 - x2 - 3x - 2 is divided by x - 1, the remainder is:

A. P(-1)
B. P(0)
C. P(1)
D. 0

15. When P(x) is divided by x - a, the factor theorem tells us that x - a

is a factor of the polynomial when:

A. P(0) = a
B. P(x - a) = 0
C. P(-a) = 0
D. P(a) = 0

3x3 - 6x2 + 2x + k
16. If has a remainder of -3, then the value of k is:
x-2
A. -7
B. -2
C. 2
D. 7

P(x) = x3 + kx2 + 5
17. Given the graph of P(x) = x3 + kx2 + 5 and the
points (2, -3) and (4, a), the value of a is: (4, a)

A. -4
B. 0
C. 1
(2, -3)
D. 5

www.math30.ca Polynomial, Radical, and Rational Functions Practice Exam

18. Potential zeros of the polynomial function P(x) = x3 + x2 - 5x + 3 are:

A. 0, 1, 3
B. -3, -1, 0
C. 0, ±1, ±3
D. ±1, ±3

19. The factored form of P(x) = x3 + 3x2 - x - 3 is:

A. P(x) = (x + 3)(x + 1)(x - 1)

B. P(x) = (x + 3)(x2 + 1)
C. P(x) = (x - 1)2(x - 3)
D. P(x) = (x + 1)2(x - 3)

20. The factored form of P(x) = x3 - 3x + 2 is:

A. P(x) = (x - 2)2(x + 1)
B. P(x) = (x + 2)2(x - 1)
C. P(x) = (x + 2)(x - 1)2
D. P(x) = (x - 2)(x - 1)2

21. The factored form of P(x) = x4 - 16 is:

A. P(x) = (x - 4)(x + 4)
B. P(x) = (x2 + 4)(x + 2)
C. P(x) = (x2 + 4)(x + 2)2
D. P(x) = (x2 + 4)(x - 2)(x + 2)

22. The polynomial function P(x) has zeros of -4, 0, 0, and 1, and the graph passes
through the point (-1, -3). The polynomial function is:

A.

B.

C.

D.

Polynomial, Radical, and Rational Functions Practice Exam www.math30.ca

23. Given the graph of P(x) = x4 + 2x3 - 5x2 - 6x and various
points on the graph, the values of a and b are:
(0, 0)
A. a = -6, b = -2 (b, 0)
(a, 0)
B. a = -5, b = -2
C. a = -4, b = -1
D. a = -3, b = -1 (2, 0)

24. Which of the following is not a solution to 3x3 + 8x2 + 4x - 1 = 0?

A.

B.

C.

D.

25. The graph of f(x) = -2x - 4 is:

A. B.

C. D.

www.math30.ca Polynomial, Radical, and Rational Functions Practice Exam

26. Given the graph of f(x) = -(x + 2)2 + 9, the graph of y = f(x) is:

A. B.

C. D.

27. Given the graph of f(x) = x2 + 0.25, the range of y = f(x) is:

A. {y | y ≥ 0.125, y ε R}
B. (0.125, ∞)
C. {y | y ≥ 0.5, y ε R}
D. (0.5, ∞)

28. The radical equation x = x + 2 has:

A. Two solutions, at x = -2 and x = 1.

B. Two solutions, at x = -1 and x = 2.
C. Only one solution at x = 1, because x = -2 is an extraneous root.
D. Only one solution at x = 2, because x = -1 is an extraneous root.

29. The radical equation 16 - x2 = 5 has:

A. No solutions, because cannot be solved algebraically.

B. No solutions, because have no point of intersection.
C. No solutions, because has no x-intercept.
D. No solutions. A, B, and C are all true.

Polynomial, Radical, and Rational Functions Practice Exam www.math30.ca

30. An equation that can be used to find the point of intersection (2, 3)
in the graphs shown is: (2, 3)

A.
B.
C.
D.

31. A ladder that is 3 m long is leaning against a wall. The base

of the ladder is d metres from the wall, and the top of the
ladder is h metres above the ground. The height of the ladder
as a function of its base distance d is:

A.

B.

C.

D.

32. If a ball at a height of h metres is dropped,

the length of time it takes to hit the ground is:

h
t=
4.9
where t is the time in seconds.
If a ball is dropped from one-quarter of its original height,
how will that change the time it takes to fall?

A. The time to fall is one-quarter the original time.

B. The time to fall is one-half the original time.
C. The time to fall is double the original time.
D. The time to fall is quadruple the original time.

www.math30.ca Polynomial, Radical, and Rational Functions Practice Exam

 1
33. The rational function f(x) = has vertical asymptotes at:
x2 - 2x - 24
A. x = -4 and x = 6.
B. x = 4 and x = -6.
C. y = -4 and y = 6.
D. y = 4 and y = -6.
1 3
34. Compared to the graph of y = , the graph of y = is:
x x+4
A. Vertically stretched by a scale factor of 3 and horizontally translated 4 units right.
B. Vertically stretched by a scale factor of 3 and horizontally translated 4 units left.
C. Horizontally stretched by a scale factor of 3 and horizontally translated 4 units right.
D. Horizontally stretched by a scale factor of 3 and horizontally translated 4 units left.

35. The illuminance of light can be described with the reciprocal-square relation:

where I is the illuminance (SI unit = lux), S is the amount of light emitted by a
source (SI unit = lumens), and d is the distance of a screen from the light source in metres.
If the original distance of the screen from the bulb is tripled, how does the illuminance change?

A. The illuminance is one-ninth the original illuminance.

B. The illuminance is one-third the original illuminance.
C. The illuminance is three times the original illuminance.
D. The illuminance is nine times the original illuminance.

36. The graph of y = x2 + 4 has:

x - 16
A. Vertical asymptotes at x = ±4 and a horizontal asymptote at y = 0.
B. Vertical asymptotes at x = ±4 and a horizontal asymptote at y = 1.
C. A vertical asymptote at x = -4, a hole when x = 4, and a horizontal asymptote at y = 0.
D. A vertical asymptote at x = 4, a hole when x = -4, and a horizontal asymptote at y = 0.

37. The graph of y = 3x

2
has:
x +9
2

A. No vertical asymptotes and a horizontal asymptote at y = 3.

B. Vertical asymptotes at x = ±3 and a horizontal asymptote at y = 0.
C. Vertical asymptotes at x = ±3 and a horizontal asymptote at y = 3.
D. Holes when x = ±3 and a horizontal asymptote at y = 3.

Polynomial, Radical, and Rational Functions Practice Exam www.math30.ca

 2
38. The graph of y = x - 5x + 6 has:
x-2
A. No vertical asymptotes and a hole at (2, -1).
B. No vertical asymptotes and a hole at (3, 0).
C. A vertical asymptote at x = 2.
D. A vertical asymptote at x = 3.

39. The graph of a rational function has a vertical asymptote at x = 0, a horizontal asymptote
at y = 0, no x-intercepts, and a hole at (-1, -1). The rational function is:

A.

B.

C.

D.

40. The rational function corresponding to the graph shown is:

A.

B.

C.

D.

6
41. The rational equation 9 = -6 has:
-
x x-1
A. Two solutions. Solving the equation algebraically yields x = -0.5 and x = 2.

B. Two solutions. The equations have points of intersection

when x = -0.5 and x = 2.

C. Two solutions. The equation has x-intercepts when x = -0.5 and x = 2.

D. Two solutions. A, B, and C are all true.

www.math30.ca Polynomial, Radical, and Rational Functions Practice Exam

42. George can canoe 24 km downstream and return to his
starting position (upstream) in 5 h. The speed of the
current is 2 km/h. What is the speed of the canoe in still water?

A rational equation that can be used to solve this problem is:

A.

B.

C.

D.

43. The shooting percentage of a hockey player is ratio of

scored goals to total shots on goal. So far this season,
Laura has scored 2 goals out of 14 shots taken.
Assuming Laura scores a goal with every shot from now on,
how many goals will she need to have a 40% shooting percentage?

A rational equation that can be used to solve this problem is:

A.

B.

C.

D.

Polynomial, Radical, and Rational Functions Practice Exam www.math30.ca

 This page has been left blank for correct booklet printing.

www.math30.ca Polynomial, Radical, and Rational Functions Practice Exam

 Polynomial, Radical, and Rational Functions Practice Exam - ANSWER KEY
Video solutions are in italics.

1. B Polynomial Functions, Example 3a 23. D Polynomial Factoring, Example 13

2. C Polynomial Functions, Example 4e 24. C Polynomial Factoring, Example 14b

3. A Polynomial Functions, Example 5a (ii) 25. B Radical Functions, Example 5d

4. C Polynomial Functions, Example 5b (iii) 26. C Radical Functions, Example 6b

5. D Polynomial Functions, Example 7b (i) 27. C Radical Functions, Example 8b

6. D Polynomial Functions, Example 9a 28. D Radical Functions, Example 10

7. B Polynomial Functions, Example 12a 29. D Radical Functions, Example 12

8. C Polynomial Functions, Example 13 (a, b) 30. C Radical Functions, Example 13b

9. D Polynomial Functions, Example 16 31. D Radical Functions, Example 14a

10. B Polynomial Division, Example 1a 32. B Radical Functions, Example 15a

11. A Polynomial Division, Example 2c 33. A Rational Functions I, Example 6b

12. C Polynomial Division, Example 3a 34. B Rational Functions I, Example 7c

13. A Polynomial Division, Example 6 35. A Rational Functions I, Example 10b

14. C Polynomial Division, Example 9b 36. D Rational Functions II, Example 1c

15. D Polynomial Division, Example 10d 37. A Rational Functions II, Example 2c

16. A Polynomial Division, Example 12b 38. A Rational Functions II, Example 7

17. D Polynomial Division, Example 15 39. C Rational Functions II, Example 8b

18. D Polynomial Factoring, Example 1b 40. D Rational Functions II, Example 9c

19. A Polynomial Factoring, Example 2a 41. D Rational Functions II, Example 11

20. C Polynomial Factoring, Example 4a 42. B Rational Functions II, Example 14

21. D Polynomial Factoring, Example 7a 43. A Rational Functions II, Example 15

22. B Polynomial Factoring, Example 9a

Polynomial, Radical, and Rational Functions Practice Exam www.math30.ca

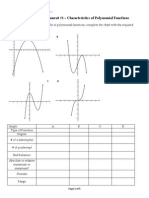
 Math 30-1 Practice Exam: Tips for Students

• Every question in the practice exam has already been covered in the Math 30-1
workbook. It is recommended that students refrain from looking at the practice exam until
they have completed their studies for the unit.

• Do not guess on a practice exam. The practice exam is a self-diagnostic tool that can be
used to identify knowledge gaps. Leave the answer blank and study the solution later.

www.math30.ca Polynomial, Radical, and Rational Functions Practice Exam