Location via proxy:   [ UP ]  
[Report a bug]   [Manage cookies]                
Scribd
Upload
99 views

3.4 Transformations of Power Functions

This document discusses transformations of power functions including cubic, quartic, and other functions with real or rational exponents. It provides examples of applying transformations to graph functions and find zeros. Exercises are included to sketch graphs using symmetry and exponent rules or transformations.

Uploaded by

Vasile Nicoleta
Copyright
© © All Rights Reserved
Available Formats
Download as PDF, TXT or read online on Scribd
99 views

3.4 Transformations of Power Functions

This document discusses transformations of power functions including cubic, quartic, and other functions with real or rational exponents. It provides examples of applying transformations to graph functions and find zeros. Exercises are included to sketch graphs using symmetry and exponent rules or transformations.

Uploaded by

Vasile Nicoleta
Copyright
© © All Rights Reserved
Available Formats
Download as PDF, TXT or read online on Scribd
You are on page 1/ 2

MHF4U - Advanced Functions

3.4 Transformations of Power Functions (Cubic, Quartic, and other)

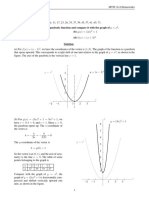
A Cubic Function Ex 1. Use transformations to graph each function.

The cubic function has the parent function f ( x)  x 3 a) f ( x)  2 x 3


and after transformations may be written as:

f ( x)  a[b( x  c)]3  d
b) f ( x)  ( x  1) 3  2
y

c) f ( x)  ( x  2) 3  3

   

 d) f ( x)  (3  x) 3  2



B Quartic Function Ex 2. Use transformations to graph each function.

The quartic function has the parent function f ( x)  x 4 a) f ( x)  ( x  2) 4


and after transformations may be written as:

f ( x)  a[b( x  c)]4  d
b) f ( x)  ( x  1) 4  3
y

c) f ( x)  2( x  1) 4  1

   

 d) f ( x)  2  (3  x) 4



Ex 3. Find the real zeros (x-intercepts) and the y- b) f ( x)  16  (2 x  1) 4


intercept.
a) f ( x)  8  ( x  2) 3

3.4 Transformations of Cubic and Quartic Functions


© 2018 Iulia & Teodoru Gugoiu - Page 1 of 2
MHF4U - Advanced Functions

C Power Function (Real Exponent)

The power function with a real exponent is defined by:

f ( x)  x  ;  R

D Power Function (Rational Exponent) Ex 4. Use symmetry and exponent rules to sketch the
graph of the following functions.
The power function with a rational exponent is defined
by: a) y  x1/ 3
f ( x)  x m / n ; n  0

where m and n are integers. b) y  x 2 / 3

c) y  x 3 / 2

d) y  x 4 / 3

e) y  x 1/ 3

f) y  x 2 / 3

Ex 5. Use transformations to sketch the graph of the Ex 6. Sketch the graph of the following functions.
following functions.
a) f ( x)  x 2 3
x 1
a) y  ( x  2)1/ 3

b) y  2  ( x  1)3 / 4

b) f ( x)  x1/ 3 ( x  8) 2 / 3

c) y  ( x  4) 3 / 2

Reading: Nelson Textbook, Pages 149-155


Homework: Nelson Textbook, Page 155: #1, 3ab, 6ab, 9, 10, 14
3.4 Transformations of Cubic and Quartic Functions
© 2018 Iulia & Teodoru Gugoiu - Page 2 of 2

You might also like