All p2 Questions (More)

Questions
Q1.
A geometric sequence has first term a and common ratio r, where r > 0
Given that
 the 3rd term is 20
 the 5th term is 12.8

(a) show that r = 0.8
(1)
(b) Hence find the value of a.
(2)
Given that the sum of the first n terms of this sequence is greater than 156
(c) find the smallest possible value of n.
(Solutions based entirely on graphical or numerical methods are not acceptable.)
(4)
(Total for question = 7 marks)
(Q07 WMA12/01, Jan 2023)

Q2.
A curve C has equation y = f(x) where

f(x) = (2 – kx)5
and k is a constant.
Given that when f(x) is divided by (4x – 5) the remainder is
(a) show that

(2)
(b) Find the first three terms, in ascending powers of x, of the binomial expansion of
giving each term in simplest form.

(3)
Using the solution to part (b) and making your method clear,
(c) find the gradient of C at the point where x = 0
(2)
(Q02 WMA12/01, Oct 2022)

Q3.
Solutions relying on calculator technology are not acceptable in this question.

(i)
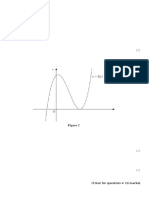
Figure 2
Figure 2 shows a sketch of part of a curve with equation
The region R, shown shaded in Figure 2, is bounded by the curve, the line with equation x =
2, the x-axis and the line with equation x = 4
Find the exact area of R.
(5)
(ii) Find the value of the constant k such that
(4)
(Q08 WMA12/01, Oct 2019)

Q4.
Figure 1 shows a sketch of the curve with equation

y = 2x2 + 7 x≥0
The finite region R, shown shaded in Figure 1, is bounded by the curve, the y-axis and the line
with equation y = 17
Find the exact area of R.
(6)
(Q04 WMA12/01, Jan 2020)

Q5.
Figure 1 shows a sketch of part of the curves C1 and C2 with equations
The curves C1 and C2 intersect at the points A and B as shown in Figure 1.

The point A has coordinates (1, 4).
Using algebra and showing all steps of your working,
(a) find the coordinates of the point B.
(4)
The finite region R, shown shaded in Figure 1, is bounded by C1 and C2
(b) Use algebraic integration to find the exact area of R.
(5)
(Q06 WMA12/01, Oct 2020)

Q6.
Figure 2 shows a sketch of part of the graph of the curves C1 and C2

The curves intersect when x = 2.5 and when x = 4
A table of values for some points on the curve C1 is shown below, with y values given to 3
decimal places as appropriate.
Using the trapezium rule with all the values of y in the table,
(a) find, to 2 decimal places, an estimate for the area bounded by the curve C1, the line with
equation x = 2.5, the x-axis
and the line with equation x = 4
(4)
The curve C2 has equation
(b) Find
(3)
The region R, shown shaded in Figure 2, is bounded by the curves C1 and C2
(c) Use the answers to part (a) and part (b) to find, to one decimal place, an estimate for the
area of the region R.
(3)
(Q05 WMA12/01, June 2021)

Q7.
In a large theatre there are n rows of seats, where n is a constant.

The number of seats in the first row is a, where a is a constant.
In each subsequent row there are 4 more seats than in the previous row so that
 in the 2nd row there are (a + 4) seats

 in the 3rd row there are (a + 8) seats
 the number of seats in each row form an arithmetic sequence
Given that the total number of seats in the first 10 rows is 360
(a) find the value of a.
(2)
Given also that the total number of seats in the n rows is 2146
(b) show that
n2 + 8n − 1073 = 0
(2)
(c) Hence
(i) state the number of rows of seats in the theatre,
(ii) find the maximum number of seats in any one row.
(3)
(Q08 WMA12/01, Oct 2023)

Q8.
A company that owned a silver mine
 extracted 480 tonnes of silver from the mine in year 1

and so on, forming an arithmetic sequence.
(a) Find the mass of silver extracted in year 14
(2)
After a total of 7770 tonnes of silver was extracted, the company stopped mining.
Given that this occurred at the end of year N,
(b) show that
N2 − 65N + 1036 = 0
(3)
(c) Hence, state the value of N.
(1)
(Q05 WMA12/01, Oct 2021)

Q9.
Wheat is grown on a farm.
 In year 1, the farm produced 300 tonnes of wheat.
 In year 12, the farm is predicted to produce 4 000 tonnes of wheat.

Model A assumes that the amount of wheat produced on the farm will increase by the same
amount each year.
(a) Using model A, find the amount of wheat produced on the farm in year 4.
Give your answer to the nearest 10 tonnes.
(3)
Model B assumes that the amount of wheat produced on the farm will increase by the same
percentage each year.
(b) Using model B, find the amount of wheat produced on the farm in year 2.
(3)
(c) Calculate, according to the two models, the difference between the total amounts of wheat
predicted to be produced on the farm from year 1 to year 12 inclusive.
(3)
(Q07 WMA12/01, Jan 2024)

Q10.
Ben is saving for the deposit for a house over a period of 60 months.
Ben saves £100 in the first month and in each subsequent month, he saves £5 more than the
previous month, so that he saves £105 in the second month, £110 in the third month, and so on,
forming an arithmetic sequence.
(a) Find the amount Ben saves in the 40th month.
(2)
(b) Find the total amount Ben saves over the 60-month period.
(3)
Lina is also saving for a deposit for a house.
Lina saves £600 in the first month and in each subsequent month, she saves £10 less than the
previous month, so that she saves £590 in the second month, £580 in the third month, and so
on, forming an arithmetic sequence.
Given that, after n months, Lina will have saved exactly £18 200 for her deposit,
(c) form an equation in n and show that it can be written as
n2 − 121n + 3640 = 0
(3)
(d) Solve the equation in part (c).
(2)
(e) State, with a reason, which of the solutions to the equation in part (c) is not a sensible value
for n.
(1)
(Q05 WMA12/01, Oct 2020)

Q11.
Given logab = k, find, in simplest form in terms of k,
(i)
(2)
(ii)
(2)
(iii)
(3)
(Q07 WMA12/01, Oct 2019)

Q12.
Kim starts working for a company.
 In year 1 her annual salary will be £16 200

 In year 10 her annual salary is predicted to be £31 500
Model A assumes that her annual salary will increase by the same amount each year.
(a) According to model A, determine Kim's annual salary in year 2.
(3)
Model B assumes that her annual salary will increase by the same percentage each year.
(b) According to model B, determine Kim's annual salary in year 2. Give your answer to the
nearest £10
(3)
(c) Calculate, according to the two models, the difference between the total amounts that Kim is
predicted to earn from year 1 to year 10 inclusive. Give your answer to the nearest £10
(3)
(Q07 WMA12/01, June 2019)

Q13.
(a) Find the first four terms, in ascending powers of x, of the binomial expansion of
(4)
(b) Given that x is small, so terms in x4 and higher powers of x may be ignored, show
where a and b are constants to be found.

(3)
(Q04 WMA12/01, June 2019)

Q14.
(a) Find the first 4 terms, in ascending powers of x, in the binomial expansion of
giving each coefficient in its simplest form.

(3)
(b) Find the term independent of x in the expansion of
(3)
(Q03 WMA12/01, Oct 2019)

Q15.
One of the terms in the binomial expansion of (3 + αx)6, where α is a constant, is 540x4
(a) Find the possible values of α.
(4)
(b) Hence find the term independent of x in the expansion of
(3)
(Q02 WMA12/01, Jan 2020)

Q16.
(a) Find the first 4 terms, in ascending powers of x, of the binomial expansion of
giving each term in its simplest form.

(4)
(b) Hence find the constant term in the series expansion of
(3)
(Q01 WMA12/01, Oct 2020)

Q17.
(a) Find the first three terms, in ascending powers of x, of the binomial expansion of
(2 + px)6
where p is a constant. Give each term in simplest form.
(4)
Given that in the expansion of
the coefficient of x2 is
(b) find the possible values of p.
(4)
(Q04 WMA12/01, Jan 2021)

Q18.
(a) Find, in ascending powers of x, up to and including the term in x3, the binomial expansion of
fully simplifying each coefficient.

(4)
(b) Use the answer to part (a) to find an approximation for 2.012513
Give your answer to 3 decimal places.
(3)
Without calculating 2.012513
(c) state, with a reason, whether the answer to part (b) is an overestimate or an underestimate.
(1)
(Q04 WMA12/01, June 2021)

Q19.
The first three terms, in ascending powers of x, of the binomial expansion of (1 + kx)16 are
1, −4x and px2
where k and p are constants.
(a) Find, in simplest form,
(i) the value of k
(ii) the value of p
(3)
Using the value of k found in part (a),

(b) find the term in x2 in the expansion of g(x).
(3)
(Q01 WMA12/01, Oct 2021)

Q20.
(a) Find the first 4 terms, in ascending powers of x, of the binomial expansion of
where k is a non-zero constant. Give each term in simplest form.

(4)
In the expansion of f(x), the constant term is 3 times the coefficient of x.

(b) Find the value of k.
(3)
(Q03 WMA12/01, Jan 2022)

Q21.
Find the first four terms, in ascending powers of x, of the binomial expansion of
Give each coefficient as an integer.
(Q01 WMA12/01, June 2022)

Q22.
The binomial expansion, in ascending powers of x, of

(3 + px)5
where p is a constant, can be written in the form
A + Bx + Cx2 + Dx3 ...
where A, B, C and D are constants.
(a) Find the value of A
(1)
Given that
 B = 18D
 p < 0
(b) find
(i) the value of p
(ii) the value of C
(6)
(Q04 WMA12/01, June 2023)

Q23.
where k is a non-zero constant

(a) Find the first 4 terms, in ascending powers of x, of the binomial expansion of f(x).
Give each term in simplest form.
(4)
Given that, in the binomial expansion of f(x), the coefficients of x, x2 and x3 are the first 3 terms of
an arithmetic progression,
(b) find, using algebra, the possible values of k.
(Solutions relying entirely on calculator technology are not acceptable.)
(3)
(Q03 WMA12/01, Jan 2023)

Q24.
(i) (a) Find, in ascending powers of x, the 2nd, 3rd and 5th terms of the binomial expansion of
(3 + 2x)6
(3)
For a particular value of x, these three terms form consecutive terms in a geometric series.
(b) Find this value of x.
(3)
(ii) In a different geometric series,
(a) Show that

5 cos2θ − 16 cos θ + 3 = 0
(3)
(b) Hence find the exact value of the 2nd term in the series.
(3)
(Q10 WMA12/01, Oct 2023)

Q25.
A scientist is using carbon-14 dating to determine the age of some wooden items.
The equation for carbon-14 dating an item is given by
N = kλt
where
 N grams is the amount of carbon-14 currently present in the item

 k grams was the initial amount of carbon-14 present in the item
 t is the number of years since the item was made
 λ is a constant, with 0 < λ < 1
(a) Sketch the graph of N against t for k = 1
(2)
Given that it takes 5700 years for the amount of carbon-14 to reduce to half its initial value,
(b) show that the value of the constant λ is 0.999878 to 6 decimal places.
(2)
Given that Item A
 is known to have had 15 grams of carbon-14 present initially

 is thought to be 3250 years old
(c) calculate, to 3 significant figures, how much carbon-14 the equation predicts is currently in
Item A.
(2)
Item B is known to have initially had 25 grams of carbon-14 present, but only 18 grams now
remain.
(d) Use algebra to calculate the age of Item B to the nearest 100 years.
(3)
(Q09 WMA12/01, June 2022)

Q26.
The circle C has centre X (3, 5) and radius r

The line l has equation y = 2x + k, where k is a constant.
(a) Show that l and C intersect when
5x2 + (4k − 26)x + k2 − 10k + 34 − r2 = 0
(3)
Given that l is a tangent to C,
(b) show that 5r2 = (k + p)2, where p is a constant to be found.
(3)
The line l
 cuts the y-axis at the point A

 touches the circle C at the point B
as shown in Figure 2.
Given that AB = 2r
(c) find the value of k
(6)
(Q10 WMA12/01, June 2022)

Q27.
Figure 2 shows a sketch of
Given that l is the tangent to C at the point N,

(a) show that an equation for the straight line passing through X and N is
2x + 5y + 7 = 0
(3)
(b) Hence find
(i) the coordinates of N,
(ii) an equation for C.
(5)
(Q07 WMA12/01, Oct 2023)

Q28.
A circle C has equation

x2 + y2 + 4x – 10y – 21 = 0
Find
(a) (i) the coordinates of the centre of C,
(ii) the exact value of the radius of C.
(3)
The point P(5, 4) lies on C.
(b) Find the equation of the tangent to C at P, writing your answer in the form y = mx + c, where
m and c are constants to be found.
(4)
(Q02 WMA12/01, June 2019)

Q29.
Figure 1
Figure 1 shows a sketch of a circle C with centre N(4, −1).
The line l with equation is a tangent to C at the point P.

Find
(a) the equation of line PN in the form y = mx + c, where m and c are constants,
(2)
(b) the equation of C.
(5)
(Q06 WMA12/01, Oct 2019)

Q30.
The circle C has equation

x2 + y2 + 6x – 4y – 14 = 0
(a) Find
(i) the coordinates of the centre of C,
(ii) the exact radius of C.
(3)
The line with equation y = k, where k is a constant, is a tangent to C.
(b) Find the possible values of k.
(2)
The line with equation y = p, where p is a negative constant, is a chord of C.
Given that the length of this chord is 4 units,
(c) find the value of p.
(3)
(Q06 WMA12/01, Jan 2020)

Q31.
The points P and Q have coordinates (−11, 6) and (−3, 12) respectively.
Given that PQ is a diameter of the circle C,
(a) (i) find the coordinates of the centre of C,
(ii) find the radius of C,
(4)
(b) Hence find an equation of C.
(2)
(c) Find an equation of the tangent to C at the point Q giving your answer in the form ax + by + c
= 0 where a, b and c are integers to be found.
(3)
(Q04 WMA12/01, Oct 2020)

Q32.
A circle C has equation

(x − k)2 + ( y − 2k)2 = k + 7
where k is a positive constant.
(a) Write down, in terms of k,
(ii) the radius of C.
(2)
Given that the point P(2, 3) lies on C
(b) (i) show that 5k2 − 17k + 6 = 0
(ii) hence find the possible values of k.
(3)
The tangent to the circle at P intersects the x-axis at point T.
Given that k < 2
(c) calculate the exact area of triangle OPT.
(5)
(Q09 WMA12/01, Jan 2021)

Q33.
A circle has equation

x2 – 6x + y2 + 8y + k = 0
where k is a positive constant.
Given that the x-axis is a tangent to this circle,
(a) find the value of k.
(3)
The circle meets the coordinate axes at the points R, S and T.
(b) Find the exact area of the triangle RST.
(4)
(Q06 WMA12/01, June 2021)

Q34.
(i) The circle C1 has equation

x2 + y2 + 10x − 12y = k where k is a constant
(a) Find the coordinates of the centre of C1
(2)
(b) State the possible range in values for k.
(2)
(ii) The point P(p, 0), the point Q(−2, 10) and the point R(8, −14) lie on a different circle, C2
Given that
 p is a positive constant
 QR is a diameter of C2
find the exact value of p.
(4)
(Q06 WMA12/01, Oct 2021)

Q35.
The points P(23, 14), Q(15, –30) and R(–7, –26) lie on the circle C, as shown in Figure 1.
(a) Show that angle PQR = 90°
(2)
(b) Hence, or otherwise, find
(i) the centre of C,
(ii) the radius of C.
(3)
Given that the point S lies on C such that the distance QS is greatest,
(c) find an equation of the tangent to C at S, giving your answer in the form ax + by + c = 0,
where a, b and c are integers to be found.
(3)
(Q06 WMA12/01, Jan 2022)

Q36.
A circle C has centre (2, 5)

Given that the point P(8, −3) lies on C
(a) (i) find the radius of C
(ii) find an equation for C
(3)
(b) Find the equation of the tangent to C at P giving your answer in the form ax + by + c = 0
where a, b and c are integers to be found.
(4)
(Q03 WMA12/01, June 2023)

Q37.
The circle C
 has centre A(3, 5)
 passes through the point B(8, – 7)

(a) Find an equation for C.
(3)
The points M and N lie on C such that MN is a chord of C.
Given that MN
 lies above the x-axis
 is parallel to the x-axis
 has length
(b) find an equation for the line passing through points M and N.
(3)
(Q03 WMA12/01, Jan 2024)

Q38.
A student was asked to prove by exhaustion that

if n is an integer then 2n2 + n + 1 is not divisible by 3
The start of the student's proof is shown in the space below.
Complete this proof.
(Q10 WMA12/01, Jan 2023)

Q39.
In this question you must show detailed reasoning.
Solutions relying entirely on calculator technology are not acceptable.
Figure 3 shows
 the curve C1 with equation y = x3 – 5x2 + 3x + 14
 the circle C2 with centre T
The point T is the minimum turning point of C1
Using Figure 3 and calculus,
(a) find the coordinates of T
(3)
The curve C1 intersects the circle C2 at the point A with x coordinate 2
(b) Find an equation of the circle C2
(3)
The line l shown in Figure 3, is the tangent to circle C2 at A
(c) Show that an equation of l is
(3)
The region R, shown shaded in Figure 3, is bounded by C1, l and the y-axis.
(d) Find the exact area of R.
(3)
(Total for question = 12 marks) (Q09 WMA12/01, Oct 2022)

Q40.
In this question you must show all stages of your working.

Figure 2 shows a sketch of part of the curve C with equation
y= x3 − 11x2 + kx where k is a constant

The point M is the maximum turning point of C and is shown in Figure 2.
Given that the x coordinate of M is 2
(a) show that k = 28
(3)
(b) Determine the range of values of x for which y is increasing.
(2)
The line l passes through M and is parallel to the x-axis.
The region R, shown shaded in Figure 2, is bounded by the curve C, the line l and the y-axis.
(c) Find, by algebraic integration, the exact area of R.
(5)
(Q08 WMA12/01, Oct 2021)

Q41.
The curve C has equation
(a) Write the equation of C in the form
where a, b, c and d are fully simplified constants.

(3)
The curve C has three turning points.
Using calculus,
(b) show that the x coordinates of the three turning points satisfy the equation
(3)
Given that the x coordinate of one of the turning points is 1
(c) find, using algebra, the exact x coordinates of the other two turning points.
(Solutions based entirely on calculator technology are not acceptable.)
(3)
(Q07 WMA12/01, Oct 2022)

Q42.
(i) Use a counter example to show that the following statement is false
"n2 + 3n + 1 is prime for all "
(2)
(ii) Use algebra to prove by exhaustion that for all
"n2 – 2 is not a multiple of 4"
(4)
(Q08 WMA12/01, Jan 2024)

Q43.
(a) Given that

3 log3(2x – 1) = 2 + log3(14x – 25)
show that
2x3 – 3x2 – 30x + 56 = 0
(4)
(b) Show that –4 is a root of this cubic equation.
(2)
(c) Hence, using algebra and showing each step of your working, solve
3 log3(2x – 1) = 2 + log3(14x – 25)
(4)
(Q07 WMA12/01, June 2021)

Q44.
(a) Sketch the curve with equation

y = a–x + 4
where a is a constant and a > 1
On your sketch show
 the coordinates of the point of intersection of the curve with the y-axis
 the equation of the asymptote to the curve.

(3)
The table above shows corresponding values of x and y for

The values of y are given to four significant figures, as appropriate.
Using the trapezium rule with all the values of y in the table,
(b) find an approximate value for
giving your answer to two significant figures.

(3)
(c) Using the answer to part (b), find an approximate value for
(3)
(Q04 WMA12/01, Jan 2024)

Q45.
(i) Solve
7 x+ 2 = 3
giving your answer in the form x = log7a where a is a rational number in its simplest form.
(3)
(ii) Using the laws of logarithms, solve
1 + log2y + log2 (y + 4) = log2 (5 − y)
(5)
(Q03 WMA12/01, Jan 2021)

Q46.
The weight of a baby mammal is monitored over a 16-month period.

The weight of the mammal, w kg, is given by
where t is the age of the mammal in months and a is a constant.

Given that the weight of the mammal was 10 kg when t = 3
(a) show that a = 1.072 correct to 3 decimal places.
(3)
Using a = 1.072
(b) find an equation for t in terms of w
(3)
(c) find the value of t when w = 15, giving your answer to 3 significant figures.
(2)
(Q04 WMA12/01, Oct 2022)

Q47.
Given a = log23
(i) write, in simplest form, in terms of a,
(a) log29
(b) log2
(3)
(ii) Solve
giving your answer, in simplest form, in terms of a.

(4)
(Q10 WMA12/01, Oct 2022)

Q48.
(a) Given 0 < a < 1, sketch the curve with equation

y = ax
showing the coordinates of the point at which the curve crosses the y-axis.
(2)
The table above shows corresponding values of x and y for

The values of y are given to 4 significant figures as appropriate.
Using the trapezium rule with all the values of y in the given table,
(b) obtain an estimate for

(3)
Using your answer to part (b) and making your method clear, estimate
(c)
(2)
(Q05 WMA12/01, Oct 2019)

Q49.
(a) Sketch the curve with equation

y = 3 × 4x
showing the coordinates of any points of intersection with the coordinate axes.
(2)
The curve with equation y = 61–x meets the curve with equation y = 3 × 4x at the point P.
(b) Show that the x coordinate of P is

(5)
(Q09 WMA12/01, Jan 2020)

Q50.
f(x) = (x2 − 2)(2x − 3) − 21

(a) State the value of the remainder when f(x) is divided by (2x − 3)
(1)
(b) Use the factor theorem to show that (x − 3) is a factor of f(x)
(2)
(c) Hence,
(i) factorise f(x)
(ii) show that the equation f(x) = 0 has only one real root.
(5)
(Q04 WMA12/01, Oct 2021)

Q51.

Solutions relying on calculator technology are not acceptable.
f(x) = 4x3 + ax2 − 29x + b
where a and b are constants.
Given that (2x + 1) is a factor of f(x),
(a) show that
a + 4b = −56
(2)
Given also that when f(x) is divided by (x − 2) the remainder is −25
(b) find a second simplified equation linking a and b.
(2)
(c) Hence, using algebra and showing your working,
(i) find the value of a and the value of b,
(ii) fully factorise f(x).
(5)
(Q04 WMA12/01, Oct 2023)

Q52.
f(x) = 3x3 + Ax2 + Bx – 10

where A and B are integers.
Given that
 when f(x) is divided by (x – 1) the remainder is k

 when f(x) is divided by (x + 1) the remainder is –10k
 k is a constant
(a) show that
11A + 9B = 83
(3)
Given also that (3x – 2) is a factor of f(x),
(b) find the value of A and the value of B.
(3)
(c) Hence find the quadratic expression g(x) such that
f(x) = (3x – 2) g(x)
(2)
(Q05 WMA12/01, Jan 2022)

Q53.
f(x) = Ax3 + 6x2 − 4x + B

where A and B are constants.
Given that
 (x + 2) is a factor of f(x)
 f(x)dx = 176
find the value of A and the value of B.
(Q07 WMA12/01, June 2022)

Q54.
(a) Given that
show that
(4)
(b) Given also that –1 is a root of the equation
(i) use algebra to find the other two roots of the equation.
(3)
(ii) Hence solve
(1)
(Q06 WMA12/01, Jan 2024)

Q55.

Solutions relying on calculator technology are not acceptable.
f(x) = 4x3 − 8x2 + 5x + a
where a is a constant.
Given that (2x − 3) is a factor of f(x),
(a) use the factor theorem to show that a = –3
(2)
(b) Hence show that the equation f(x) = 0 has only one real root.
(4)
(Q02 WMA12/01, June 2023)

Q56.
The circle C has equation

x2 + y2 + 8x – 4y = 0
(a) Find
(ii) the exact radius of C.
(3)
The point P lies on C.
Given that the tangent to C at P has equation x + 2y + 10 = 0
(b) find the coordinates of P
(4)
(c) Find the equation of the normal to C at P, giving your answer in the form y = mx + c where m
and c are
integers to be found.
(3)
(Q06 WMA12/01, Jan 2023)

Q57.
f(x) = x3 + (p + 3) x2 – x + q
where p and q are constants and p > 0
Given that (x – 3) is a factor of f(x)
(a) show that
9p + q = –51
(2)
Given also that when f(x) is divided by (x + p) the remainder is 9
(b) show that
3p2 + p + q – 9 = 0
(2)
(c) Hence find the value of p and the value of q.
(3)
(d) Hence find a quadratic expression g(x) such that
f(x) = (x – 3) g(x)
(2)
(Q05 WMA12/01, Jan 2023)

Q58.
A sequence a1, a2, a3, ... is defined by

an + 1 = 4 – an
a1 = 3
Find the value of
(a) (i) a2
(ii) a107
(2)
(b)
(2)
(Q01 WMA12/01, June 2019)

Q59.
A sequence α1, α2, α3, ... is defined by
where p is a constant.
(a) Find an expression for α2 in terms of p, giving your answer in simplest form.
(1)
Given that an
(b) find the possible values of α2
(6)
(Q08 WMA12/01, Jan 2021)

Q60.
In a geometric sequence u1, u2, u3, ...
 the common ratio is r

 u2 + u3 = 6
 u4 = 8
(a) Show that r satisfies
3r2 − 4r − 4 = 0
(3)
Given that the geometric sequence has a sum to infinity,
(b) find u1
(3)
(c) find S∞
(2)
(Q06 WMA12/01, June 2022)

Q61.
A geometric sequence has first term a and common ratio r

Given that S∞ = 3a
(a) show that

(2)
Given also that
where uk is the kth term of this sequence,

(b) find the value of S10 giving your answer to one decimal place.
(5)
(Q08 WMA12/01, Oct 2022)

Q62.
The adult population of a town at the start of 2019 is 25 000

A model predicts that the adult population will increase by 2% each year, so that the number of
adults in the population at the start of each year following 2019 will form a geometric sequence.
(a) Find, according to the model, the adult population of the town at the start of 2032
(3)
It is also modelled that every member of the adult population gives £5 to local charity at the start
of each year.
(b) Find, according to these models, the total amount of money that would be given to local
charity by the adult population of the town from 2019 to 2032 inclusive. Give your answer to the
nearest £1 000
(3)
(Q02 WMA12/01, Oct 2019)

Q63.

A software developer released an app to download.
The numbers of downloads of the app each month, in thousands, for the first three months after
the app was released were
2k – 15 k k+4
where k is a constant.
Given that the numbers of downloads each month are modelled as a geometric series,
(a) show that k2 – 7k – 60 = 0
(2)
(b) predict the number of downloads in the 4th month.
(4)
The total number of all downloads of the app is predicted to exceed 3 million for the first time in
the Nth month.
(c) Calculate the value of N according to the model.
(Q06 WMA12/01, June 2023)

Q64.

Figure 3 shows a sketch of part of the curve C with equation
(a) Find, using calculus, the range of values of x for which y is increasing.
(4)
The point P lies on C and has coordinates (9, 40).
The line l is the tangent to C at the point P.
The finite region R, shown shaded in Figure 3, is bounded by the curve C, the line l, the x-axis
and the y-axis.
(b) Find, using calculus, the exact area of R.
(8)
(Q09 WMA12/01, Oct 2023)

Q65.
Figure 2 shows
 the curve C with equation y = x – x2

 the line l with equation y = mx, where m is a constant and 0 < m < 1
The line and the curve intersect at the origin O and at the point P.
(a) Find, in terms of m, the coordinates of P.
(2)
The region R1, shown shaded in Figure 2, is bounded by C and l.
(b) Show that the area of R1 is
(5)
The region R2, also shown shaded in Figure 2, is bounded by C, the x-axis and l.
Given that the area of R1 is equal to the area of R2
(c) find the exact value of m.
(3)
(Q09 WMA12/01, Jan 2022)

Q66.
The curve C1 has equation y = f(x).
A table of values of x and y for y = f(x) is shown below, with the y values rounded to 4 decimal
places where appropriate.
(a) Use the trapezium rule with all the values of y in the table to find an approximation for
giving your answer to 3 decimal places.

(3)
The region R, shown shaded in Figure 1, is bounded by

 the curve C1
 the curve C2 with equation y = 2 –

 the line with equation x = 2
 the y-axis
The region R forms part of the design for a logo shown in Figure 2.
The design consists of the shaded region R inside a rectangle of width 2 and height 3
Using calculus and the answer to part (a),
(b) calculate an estimate for the percentage of the logo which is shaded.
(4)

(Q06 WMA12/01, Oct 2022)
Q67.

Give your answers in fully simplified surd form.
Given that a and b are positive constants, solve the simultaneous equations
a−b=8
log4a + log4b = 3
(Q04 WMA12/01, June 2022)

Q68.
Use the laws of logarithms to solve

log2 (16x) + log2 (x + 1) = 3 + log2 (x + 6)
(Q05 WMA12/01, June 2023)

Q69.

(i) Solve
3a = 70
giving the answer to 3 decimal places.
(2)
(ii) Find the exact value of b such that
4 + 3 log3b = log3 5b
(4)
(Q05 WMA12/01, Oct 2023)

Q70.
(i) Find the exact solution of the equation

82x + 1 = 6
giving your answer in the form a + b log2 3, where a and b are constants to be found.
(4)
(ii) Using the laws of logarithms, solve
log5(7 – 2y) = 2 log5(y + 1) – 1
(5)
(Q08 WMA12/01, June 2019)

Q71.
(i) Find the exact value of x for which

log3(x + 5) − 4 = log3(2x − 1)
(4)
(ii) Given that
3y + 3 × 21 − 2y = 108
(a) show that
0.75y = 2
(4)
(b) Hence find the value of y, giving your answer to 3 decimal places.
(2)
(Q09 WMA12/01, Oct 2020)

Q72.
Using the laws of logarithms, solve

log3 (32 – 12x) = 2 log3 (1 – x) + 3
(Q04 WMA12/01, Jan 2022)

Q73.

(a) Find , giving each term in simplest form.

(2)
(b) Hence find the coordinates of the stationary point of C.
(4)
(c) Find and hence determine the nature of the stationary point of C.
(2)
(Q02 WMA12/01, Jan 2022)

Q74.
A sequence u1 , u2 , u3 , ... is defined by
(a) Find the value of u2 , the value of u3 and the value of u4

(3)
(b) Find the value of
(2)
(Q02 WMA12/01, Oct 2023)

Q75.
(i) Use algebra to prove that for all real values of x

(x – 4)2 ≥ 2x – 9
(3)
(ii) Show that the following statement is untrue.
2n + 1 is a prime number for all values of n, n
(1)
(Q03 WMA12/01, June 2019)

Q76.
(i) Use algebra to prove that for all x ≥ 0
(3)
(ii) Show that the following statement is not true.
"The sum of three consecutive prime numbers is always a multiple of 5"
(1)
(Q05 WMA12/01, Jan 2021)

Q77.
(i) Prove that for all single digit prime numbers, p,

p3 + p is a multiple of 10
(2)
(ii) Show, using algebra, that for n ∈
(n + 1)3 – n3 is not a multiple of 3
(3)
(Q03 WMA12/01, June 2021)

Q78.
(a) Prove that for all positive values of x and y,
(3)
(b) Prove by counter-example that this inequality does not hold when x and y are both negative.
(1)
(Q09 WMA12/01, Oct 2021)

Q79.
(i) Prove by counter example that the statement

"if p is a prime number then 2p + 1 is also a prime number"
is not true.
(1)
(ii) Use proof by exhaustion to prove that if n is an integer then
5n2 + n + 12
is always even.
(4)
(Q10 WMA12/01, Jan 2022)

Q80.
Given that a, b and c are integers greater than 0 such that
 c = b + 2
 a + b + c = 10
Prove, by exhaustion, that the product of a, b and c is always even.
You may use the table below to illustrate your answer.
(3)
(Q01 WMA12/01, Oct 2022)

Q81.
Given that a, b and c are integers greater than 0 such that
 c = 3a + 1
 a + b + c = 15
prove, by exhaustion, that the product abc is always a multiple of 4
You may use the table below to illustrate your answer.
(3)
You may not need to use all rows of this table.
(Q01 WMA12/01, Oct 2023)

Q82.
(i) A student writes the following statement:

When a and b are consecutive prime numbers, a2 + b2 is never a multiple of 10
Prove by counter example that this statement is not true.
(2)
(ii) Given that x and y are even integers greater than 0 and less than 6, prove by exhaustion,
that
(3)
(Q08 WMA12/01, June 2023)

Q83.
(i) Show that the following statement is false:

"(n + 1)3 − n3 is prime for all n ∈ "
(2)
(ii) Given that the points A(1, 0), B(3, −10) and C(7, −6) lie on a circle, prove that AB is a
diameter of this circle.
(5)
(Q03 WMA12/01, June 2022)

Q84.
(i) An arithmetic series has first term α and common difference d.

Prove that the sum to n terms of this series is
(3)
(ii) A sequence u1, u2, u3,... is given by
un = 5n + 3(–1)n
Find the value of
(a) u5
(1)
(b)
(3)
(Q08 WMA12/01, Jan 2020)

Q85.
A geometric series has first term a and common ratio r.

(a) Prove that the sum of the first n terms of this series is given by
(3)
The second term of a geometric series is −320 and the fifth term is
(b) Find the value of the common ratio.
(2)
(c) Hence find the sum of the first 13 terms of the series, giving your answer to 2 decimal places.
(3)
(Q08 WMA12/01, Oct 2020)

Q86.
f(x) = (x − 3)(3x2 + x + a) − 35 where a is a constant

(a) State the remainder when f(x) is divided by (x − 3).
(1)
Given (3x − 2) is a factor of f(x),
(b) show that a = −17
(2)
(c) Using algebra and showing each step of your working, fully factorise f(x).
(5)
(Q04 WMA12/01, Oct 2019)

Q87.
f(x) = ax3 − x2 + bx + 4
When f(x) is divided by (x + 4), the remainder is −108
(a) Use the remainder theorem to show that
16a + b = 24
(2)
Given also that (2x − 1) is a factor of f(x),
(b) find the value of a and the value of b.
(3)
(c) Find f'(x).
(1)
(d) Hence find the exact coordinates of the stationary points of the curve with equation y = f(x).
(4)
(Q03 WMA12/01, Oct 2020)

Q88.
f(x) = x4 + ax3 − 3x2 + bx + 5

When f(x) is divided by (x + 1), the remainder is 4
(a) Show that a + b = −1
(2)
When f(x) is divided by (x − 2) , the remainder is −23
(b) Find the value of a and the value of b.
(4)
(Q01 WMA12/01, Jan 2021)

Q89.
f(x) = kx3 – 15x2 – 32x – 12 where k is a constant

Given (x – 3) is a factor of f(x),
(a) show that k = 9
(2)
(b) Using algebra and showing each step of your working, fully factorise f(x).
(4)
(c) Solve, for 0 ≤ θ < 360°, the equation
9 cos3θ – 15 cos2θ – 32 cos θ – 12 = 0
giving your answers to one decimal place.
(2)
(Q06 WMA12/01, June 2019)

Q90.
f(x) = ax3 + 3x2 – 8x + 2 where a is a constant

Given that when f(x) is divided by (x – 2) the remainder is 3, find the value of a.
(Q01 WMA12/01, Jan 2024)

Q91.

Owen wants to train for 12 weeks in preparation for running a marathon.
During the 12-week period he will run every Sunday and every Wednesday.
 On Sunday in week 1 he will run 15 km

 On Sunday in week 12 he will run 37 km
He considers two different 12-week training plans.
In training plan A, he will increase the distance he runs each Sunday by the same amount.
(a) Calculate the distance he will run on Sunday in week 5 under training plan A.
(3)
In training plan B, he will increase the distance he runs each Sunday by the same percentage.
(b) Calculate the distance he will run on Sunday in week 5 under training plan B. Give your
answer in km to one decimal place.
(3)
Owen will also run a fixed distance, x km, each Wednesday over the 12-week period.
Given that
 x is an integer
 the total distance that Owen will run on Sundays and Wednesdays over the 12 weeks will
not exceed 360 km
(c) (i) find the maximum value of x, if he uses training plan A,
(ii) find the maximum value of x, if he uses training plan B.
(5)
(Q10 WMA12/01, Jan 2021)

Q92.
Adina is saving money to buy a new computer. She saves Â£5 in week 1, £5.25 in week 2, £5.50
in week 3 and so on until she
has enough money, in total, to buy the computer.
She decides to model her savings using either an arithmetic series or a geometric series.
Using the information given,
(a) (i) state with a reason whether an arithmetic series or a geometric series should be used,
(ii) write down an expression, in terms of n, for the amount, in pounds (£), saved in week n.
(3)
Given that the computer Adina wants to buy costs £350
(b) find the number of weeks it will take for Adina to save enough money to buy the computer.
(4)
(Q01 WMA12/01, June 2021)

Q93.
A sequence u1, u2, u3, ... is defined by

un+1 = b − aun
u1 = 3
(a) Find, in terms of a and b,
(i) u2
(ii) u3
(2)
Given

 b = a + 9
(b) show that
a2 − 5a – 66 = 0
(3)
(c) Hence find the larger possible value of u2
(3)
(Q11 WMA12/01, June 2023)

Q94.
A colony of bees is being studied.

The number of bees in the colony at the start of the study was 30 000
Three years after the start of the study, the number of bees in the colony is 34 000
A model predicts that the number of bees in the colony will increase by p % each year, so that
the number of bees in the colony at the end of each year of study forms a geometric sequence.
Assuming the model,
(a) find the value of p, giving your answer to 2 decimal places.
(3)
According to the model, at the end of N years of study the number of bees in the colony exceeds
75 000
(b) Find, showing all steps in your working, the smallest integer value of N.
(5)
(Q05 WMA12/01, Jan 2020)

Q95.
A sequence a1, a2, a3, ... is defined by
Find the exact values of

(a) (i) a1
(ii) a2
(iii) a3
(3)
(b) Hence find the exact value of
You must make your method clear.

(4)
(Q03 WMA12/01, Oct 2022)

Q96.
A metal post is repeatedly hit in order to drive it into the ground.

Given that
 on the 1st hit, the post is driven 100 mm into the ground
 on the 2nd hit, the post is driven an additional 98 mm into the ground
 on the 3rd hit, the post is driven an additional 96 mm into the ground
 the additional distances the post travels on each subsequent hit form an arithmetic
sequence
(a) show that the post is driven an additional 62 mm into the ground with the 20th hit.
(1)
(b) Find the total distance that the post has been driven into the ground after 20 hits.
(2)
Given that for each subsequent hit after the 20th hit
 the additional distances the post travels form a geometric sequence with common ratio r
 on the 22nd hit, the post is driven an additional 60 mm into the ground
(c) find the value of r, giving your answer to 3 decimal places.
(2)
After a total of N hits, the post will have been driven more than 3 m into the ground.
(d) Find, showing all steps in your working, the smallest possible value of N.
(4)
(Q08 WMA12/01, Jan 2022)

Q97.

Solutions based entirely on calculator technology are not acceptable.
A brick is in the shape of a cuboid with width x cm, length 3x cm and height h cm, as shown in
Figure 2.
The volume of the brick is 972 cm3
(a) Show that the surface area of the brick, S cm2, is given by
(3)
(b) Find
(1)
(c) Hence find the value of x for which S is stationary.
(2)
(d) Find and hence show that the value of x found in part (c) gives the minimum value of S.
(2)
(e) Hence find the minimum surface area of the brick.
(1)

(Q02 WMA12/01, Jan 2023)
Q98.
(i) A geometric sequence has first term 4 and common ratio 6

Given that the nth term is greater than 10100, find the minimum possible value of n.
(3)
(ii) A different geometric sequence has first term a and common ratio r.
Given that
 the second term of the sequence is −6

 the sum to infinity of the series is 25
(a) show that
25r2 − 25r − 6 = 0
(3)
(b) Write down the solutions of
25r2 − 25r − 6 = 0
(1)
Hence,
(c) state the value of r, giving a reason for your answer,
(1)
(d) find the sum of the first 4 terms of the series.
(2)
(Q07 WMA12/01, Oct 2021)

Q99.

Solutions based entirely on calculator technology are not acceptable.
(i) Solve, for the equation

5 sin (3x + 0.1) + 2 = 0
giving your answers, in radians, to 2 decimal places.
(4)
(ii) Solve, for 0 < θ < 360°, the equation
2 tanθ sinθ = 5 + cosθ
giving your answers, in degrees, to one decimal place.
(5)
(Q08 WMA12/01, Jan 2023)

Q100.
A company makes a particular type of watch.

The annual profit made by the company from sales of these watches is modelled by the equation
where P is the annual profit measured in thousands of pounds and £x is the selling price of the
watch.
According to this model,
(a) find, using calculus, the maximum possible annual profit.
(6)
(b) Justify, also using calculus, that the profit you have found is a maximum.
(2)
(Q05 WMA12/01, June 2019)

Q101.
A curve C has equation y = 2x2(x − 5)

(a) Find, using calculus, the x coordinates of the stationary points of C.
(4)
(b) Hence find the values of x for which y is increasing.
(2)
(Q01 WMA12/01, Oct 2019)

Q102.
A curve C has equation
where k is a constant.
The point P with x coordinate lies on C.

Given that P is a stationary point of C,
(a) show that

(4)
(b) Determine the nature of the stationary point at P, justifying your answer.
(2)
The curve C has a second stationary point.
(c) Using algebra, find the x coordinate of this second stationary point.
(4)
(Q10 WMA12/01, Jan 2020)

Q103.
A curve has equation

y = x3 − x2 − 16x + 2
(a) Using calculus, find the x coordinates of the stationary points of the curve.
(4)
(b) Justify, by further calculus, the nature of all of the stationary points of the curve.
(3)
(Q02 WMA12/01, Jan 2021)

Q104.

y = ax3 − 3x2 + 3x + b
Given that
• the point (2, 5) lies on C
• the gradient of the curve at (2, 5) is 7
(a) find the value of a and the value of b.
(4)
(b) Prove that C has no turning points.
(3)
(Q10 WMA12/01, Oct 2019)

Q105.
Figure 1
Figure 1 shows a sketch of part of the curve C with equation y = f(x) where
Using calculus,
(a) find the range of values of x for which f(x) is increasing,
(4)
(b) show that

(4)
The point P(2, 0) and the point Q(6, 0) lie on C.
Given
(c) (i) state the value of
(ii) find the value of the constant k such that

(3)
(Q10 WMA12/01, June 2019)

Q106.
(i) Find the value of
(3)
(ii) A sequence u1, u2, u3,... is defined by
(a) Show that this sequence is periodic.

(2)
(b) State the order of this sequence.
(1)
(c) Hence find
(2)
(Q05 WMA12/01, Jan 2024)

Q107.
(i) Using the laws of logarithms, solve

log3(4x) + 2 = log3(5x + 7)
(3)
(ii) Given that
find y in terms of a, giving your answer in simplest form.

(3)
(Q04 WMA12/01, Jan 2023)

Q108.
(a) Complete the table below, giving the values of y to 3 decimal places.
(1)
(b) Use the trapezium rule, with all the values of y from the completed table, to find an
approximate value for
(3)
(Q02 WMA12/01, Oct 2020)

Q109.
Solar panels are installed on the roof of a building.

The power, P, produced on a particular day, in kW, can be modelled by the equation
P = 0.95 + 2t − 12 + 212 − t − (t − 12)2 8.5 ≤ t ≤ 15.2
where t is the time in hours after midnight. The graph of P against t is shown in Figure 1.
A table of values of t and P is shown below, with the values of P given to 4 significant figures
where appropriate.
(a) Use the given equation to complete the table, giving the values of P to 4 significant figures
where appropriate.
(2)
The amount of energy, in kWh, produced between 10:00 and 12:00 can be found by calculating
the area of region R, shown shaded in Figure 1.
(b) Use the trapezium rule, with all the values of P in the completed table, to find an estimate for
the amount of energy produced between 10:00 and 12:00. Give your answer to 2 decimal places.
(4)
(Q07 WMA12/01, Jan 2021)

Q110.
The table below shows corresponding values of x and y for
The values of y are given to 3 decimal places.
(a) obtain an estimate for

(3)
(b) Using your answer to part (a) and making your method clear, estimate
(i)
(ii)
(4)
(Q01 WMA12/01, Jan 2022)

Q111.
Figure 1 shows the graph of

y = 1 − log10 (sin x) 0<x<π
where x is in radians.
The table below shows some values of x and y for this graph, with values of y given to 3 decimal
places.
(a) Complete the table above, giving values of y to 3 decimal places.

(2)
(b) Use the trapezium rule with all the y values in the completed table to find, to 2 decimal
places, an estimate for
(3)
(c) Use your answer to part (b) to find an estimate for
(3)
(Q02 WMA12/01, June 2022)

Q112.
The continuous curve C has equation y = f(x).

A table of values of x and y for y = f(x) is shown below.
Use the trapezium rule with all the values of y in the table to find an approximation for
(Q01 WMA12/01, June 2023)

Q113.
A river is being studied.

At one particular place, the river is 15 m wide.
The depth, y metres, of the river is measured at a point x metres from one side of the river.
Figure 1 shows a plot of the cross-section of the river and the coordinate values (x, y)
(a) Use the trapezium rule with all the y values given in Figure 1 to estimate the cross-sectional
area of the river.
(3)
The water in the river is modelled as flowing at a constant speed of 1.5 m s −1 across the whole of
the cross-section.
(b) Use the model and the answer to part (a) to estimate the volume of water flowing through
this section of the river each minute, giving your answer in m 3 to 2 significant figures.
(2)
Assuming the model,
(c) state, giving a reason for your answer, whether your answer for part (b) is an overestimate or
an underestimate of the true volume of water flowing through this section of the river each
minute.
(1)
(Q06 WMA12/01, Oct 2023)

Q114.
Figure 1 shows a sketch of part of the curve with equation y = log10x

The region R, shown shaded in Figure 1, is bounded by the curve, the line with equation x = 2,
the x-axis and the line with equation x = 14
Using the trapezium rule with four strips of equal width,
(a) show that the area of R is approximately 10.10
(3)
(b) Explain how the trapezium rule could be used to obtain a more accurate estimate for the
area of R.
(1)
(c) Using the answer to part (a) and making your method clear, estimate the value of
(4)
(Q03 WMA12/01, Oct 2021)

Q115.
The table below shows corresponding values of x and y for y = log2 (2x)
The values of y are given to 2 decimal places as appropriate.
(a) obtain an estimate for , giving your answer to one decimal place.
(3)
Using your answer to part (a) and making your method clear, estimate
(b) (i)
(ii)
(4)
(Q01 WMA12/01, Jan 2020)

Q116.

(i) Solve, for
(5)
(ii) Solve, for 0 < θ < 360°
(2 sin θ − cos θ)2 = 1
giving your answers, as appropriate, to one decimal place.
(5)
(Q10 WMA12/01, Oct 2021)

Q117.

Solve, for −180° < θ ≤ 180°, the equation
3tan(θ + 43°) = 2cos(θ + 43°)
(Q05 WMA12/01, June 2022)

Q118.

(a) Solve, for 0 < θ ≤ 360° the equation
2 tan θ + 3 sin θ = 0
giving your answers, as appropriate, to one decimal place.
(5)
(b) Hence, or otherwise, find the smallest positive solution of
2 tan (2x + 40°) + 3 sin (2x + 40°) = 0
giving your answer to one decimal place.
(2)
(Q03 WMA12/01, Oct 2023)

Q119.
(a) Show that the equation

cos θ – 1 = 4 sin θ tan θ
can be written in the form
5 cos2θ – cos θ – 4 = 0
(4)
(b) Hence solve, for

cos 2x – 1 = 4 sin 2x tan 2x
giving your answers, where appropriate, to 2 decimal places.
(4)
(Q09 WMA12/01, June 2019)

Q120.

8 tan θ = 3 cos θ
may be rewritten in the form
3 sin2θ + 8 sin θ – 3 = 0
(3)
(b) Hence solve, for 0 ≤ x ≤ 90°, the equation
8 tan 2x = 3 cos 2x
giving your answers to 2 decimal places.
(4)
(Q07 WMA12/01, Jan 2020)

Q121.
(i) Show that
(3)
(ii) Solve, for 0 ≤ x < 90°, the equation
3 cos2 (2x + 10°) = 1
giving your answers in degrees to one decimal place.
(Solutions based entirely on graphical or numerical methods are not acceptable.)
(4)
(Q07 WMA12/01, Oct 2020)

Q122.

3 sin3θ + 10 sin2θ − 8 sin θ = 0
(4)
(b) Hence solve, for
giving your answers to 3 decimal places where appropriate.

(4)
(Q06 WMA12/01, Jan 2021)

Q123.

(i) Solve, for 0 < θ < 360°, the equation
3 sin (θ + 30°) = 7 cos (θ + 30°)
(4)
(ii) (a) Show that the equation
3 sin3x = 5 sin x – 7 sin x cos x
sin x (a cos 2x + b cos x + c) = 0
where a, b and c are constants to be found.
(b) Hence solve for the equation

3 sin3x = 5 sin x – 7 sin x cos x
(6)
(Q08 WMA12/01, June 2021)

Q124.
Solutions based entirely on graphical or numerical methods are not acceptable in this
question.
(i) Solve, for 0 ≤ θ <180°, the equation
3 sin (2θ − 10°) = 1
(4)
(ii) The first three terms of an arithmetic sequence are
where α is a constant.
(a) Show that 2 cos α = 3 sin2α
(3)
Given that π < α < 2π,
(b) find, showing all working, the value of α to 3 decimal places.
(5)
(Q09 WMA12/01, Oct 2019)

Q125.

(a) Show that
3 cos θ (tan θ sin θ + 3) = 11 – 5cos θ
may be written as
3 cos2θ – 14 cos θ + 8 = 0
(3)
(b) Hence solve, for 0 < x < 360°
3 cos 2x (tan 2x sin 2x + 3) = 11 – 5cos 2x
(4)
(Q09 WMA12/01, June 2023)

Q126.

(i) Solve, for 0 ≤ x < 360°, the equation
sin x tan x = 5
(6)
(ii)
Figure 1 shows a sketch of part of the curve with equation
where A is a constant and θ is measured in radians.

The points P, Q and R lie on the curve and are shown in Figure 1.
Given that the y coordinate of P is 7
(a) state the value of A,
(1)
(b) find the exact coordinates of Q,
(3)
(c) find the value of θ at R, giving your answer to 3 significant figures.
(4)
(Q09 WMA12/01, Jan 2024)

Q127.

(i) Solve, for –90° < x < 90°, the equation
3 sin (2x – 15°) = cos (2x – 15°)
(4)
(ii) Solve, for 0 < θ < 2π, the equation
4 sin2θ + 8 cos θ = 3
giving your answers to 3 significant figures.
(4)
(Q07 WMA12/01, Jan 2022)

Q128.

can be written as
(3)
(b) Hence solve for
(5)
(Q05 WMA12/01, Oct 2022)

Q129.
f(x) = 6x3 + 17x2 + 4x – 12

(a) Use the factor theorem to show that (2x + 3) is a factor of f(x).
(2)
(b) Hence, using algebra, write f(x) as a product of three linear factors.
(4)
(c) Solve, for , the equation

6 tan3θ + 17 tan2θ + 4 tan θ – 12 = 0
giving your answers to 3 significant figures.
(2)
(Q03 WMA12/01, Jan 2020)

Q130.

Figure 2 shows a sketch of the curve with equation
The point P is the only stationary point on the curve.

(a) Use calculus to show that the x coordinate of P is 9
(4)
The line l passes through the point P and is parallel to the x-axis.
The region R, shown shaded in Figure 2, is bounded by the curve, the line l and the line with
equation x = 4
(b) Use algebraic integration to find the exact area of R.
(5)
(Q10 WMA12/01, Jan 2024)

Q131.
Figure 1 shows a sketch of part of the curve with equation y = f(x)

The table below shows some corresponding values of x and y for this curve.
The values of y are given to 3 decimal places.
(a) obtain an estimate for

(3)
(b) Use your answer to part (a) to estimate
(3)
(Total for question = 6 marks) (Q01 WMA12/01, Jan 2023)

All p2 Questions (More)

Uploaded by

Copyright:

Available Formats

All p2 Questions (More)

Uploaded by

Document Information

Original Title

Copyright

Available Formats

Share this document

Share or Embed Document

Sharing Options

Did you find this document useful?

Is this content inappropriate?

Copyright:

Available Formats

All p2 Questions (More)

Uploaded by

Copyright:

Available Formats

Questions

 the 3rd term is 20

 the 5th term is 12.8

(Total for question = 7 marks)

(Q07 WMA12/01, Jan 2023)

A curve C has equation y = f(x) where

Given that when f(x) is divided by (4x – 5) the remainder is

(a) show that

giving each term in simplest form.

(Total for question = 7 marks)

(Q02 WMA12/01, Oct 2022)

Solutions relying on calculator technology are not acceptable in this question.

(Total for question = 9 marks)

(Q08 WMA12/01, Oct 2019)

Figure 1 shows a sketch of the curve with equation

(Total for question = 6 marks)

(Q04 WMA12/01, Jan 2020)

Figure 1 shows a sketch of part of the curves C1 and C2 with equations

The curves C1 and C2 intersect at the points A and B as shown in Figure 1.

(Q06 WMA12/01, Oct 2020)

Figure 2 shows a sketch of part of the graph of the curves C1 and C2

(Q05 WMA12/01, June 2021)

In a large theatre there are n rows of seats, where n is a constant.

 in the 2nd row there are (a + 4) seats

(Total for question = 7 marks)

(Q08 WMA12/01, Oct 2023)

A company that owned a silver mine

 extracted 480 tonnes of silver from the mine in year 1

(Total for question = 6 marks)

(Q05 WMA12/01, Oct 2021)

Wheat is grown on a farm.

 In year 1, the farm produced 300 tonnes of wheat.

 In year 12, the farm is predicted to produce 4 000 tonnes of wheat.

(Total for question = 9 marks)

(Q07 WMA12/01, Jan 2024)

(Total for question = 11 marks)

(Q05 WMA12/01, Oct 2020)

Given logab = k, find, in simplest form in terms of k,

(Total for question = 7 marks)

(Q07 WMA12/01, Oct 2019)

Kim starts working for a company.

 In year 1 her annual salary will be £16 200

(Total for question = 9 marks)

(Q07 WMA12/01, June 2019)

where a and b are constants to be found.

(Total for question = 7 marks)

(Q04 WMA12/01, June 2019)

giving each coefficient in its simplest form.

(Total for question = 6 marks)

(Q03 WMA12/01, Oct 2019)

(Total for question = 7 marks)

(Q02 WMA12/01, Jan 2020)

giving each term in its simplest form.

(Total for question = 7 marks)

(Q01 WMA12/01, Oct 2020)

(Total for question = 8 marks)

(Q04 WMA12/01, Jan 2021)

fully simplifying each coefficient.

(Total for question = 8 marks)