Chapter13BinaryandMixed IntegerProgramming
Uploaded by
sunfleurstoreChapter13BinaryandMixed IntegerProgramming
Uploaded by
sunfleurstoreChapter 13: Binary and Mixed-Integer Programming
The general branch and bound approach described in the previous chapter can be customized for
special situations. This chapter addresses two special situations:
when all of the variables are binary (known as “Binary Integer Programming” or BIP),
when some or all of the variables are integer-valued and the objective function and all of
the constraints are linear (known as “Mixed Integer Programming”, MIP, or “Mixed
Integer Linear Programming”, MILP).
Binary Integer Programming
In binary problems, each variable can only take on the value of 0 or 1. This may represent the
selection or rejection of an option, the turning on or off of switches, a yes/no answer, or many
other situations. We will study a specialized branch and bound algorithm for solving BIPs,
known as Balas Additive Algorithm. It requires that the problem be put into a standard form:
The objective function has the form minimize Z j 1 c j x j
n
The m constraints are all inequalities of the form ax ij j bi for i 1,2,...m
All of the xj where j=1,2,…n are binary variables (can only have a value of 0 or 1).
All objective function coefficients are non-negative.
The variables are ordered according to their objective function coefficients so that
0 ≤ c1 ≤ c2 ≤…≤ cn.
This may seem like a restrictive set of conditions, but many problems are easy to convert to this
form. For example, negative objective function coefficients are handled by a change of variables
in which xj is replaced by (1-xj’). It is also easy to reorder the variables. Constraint right hand
sides can be negative, so constraints are easily converted to form by multiplying through by
-1. The biggest restriction is that Balas Additive Algorithm does not handle equality constraints.
The keys to how Balas Algorithm works lies in its special structure:
The objective function sense is minimization, and all of the coefficients are nonnegative,
so we would prefer to set all of the variables to zero to give the smallest value of Z.
If we cannot set all of the variables to 0 without violating one or more constraints, then
we prefer to set the variable that has the smallest index to 1. This is because the variables
are ordered so that those earlier in the list increase Z by the smallest amount.
These features also affect the rest of the branch and bound procedures. Branching is simple:
each variable can only take on one of two values: 0 or 1. Bounding is the interesting part. Balas
algorithm does not perform any kind of look-ahead to try to complete the solution or a simplified
version of it. Instead the bounding function just looks at the cost of the next cheapest solution
that might provide a feasible solution. There are two cases, as described next.
Practical Optimization: a Gentle Introduction John W. Chinneck, 2015
1
http://www.sce.carleton.ca/faculty/chinneck/po.html
If the current variable is set to 1, i.e. xN = 1, then the algorithm assumes that this might provide a
feasible solution, so the value of the bound is j 1 c j x j . Because of the variable ordering, this is
N
the cheapest thing that can happen. Note that xN (“x now”) is not the same as xn (the last x in the
list).
If the current variable is set to 0, i.e. xN = 0, then things are a little different. Recall that we need
to calculate a bounding function value only for nodes that are currently infeasible. In this case,
one of the constraints is not yet satisfied, i.e. the left hand side is less than the right hand
constant. But if we set the current variable to zero, the left hand side value of the violated
constraint(s) will not change. Therefore we must set at least one more variable to 1, and the
cheapest one available is xN+1, so the bounding function value is j 1 c j x j cN 1 . As before, the
N
algorithm assumes that this cheapest setting might provide a feasible solution, so it proceeds.
It is easy to determine whether the solution proposed by the bounding function is feasible: just
assume that all of the variables past xN (when xN = 1) or past xN+1 (when xN = 0) take on the value
of zero and check all of the constraints. If all of the constraints are satisfied at the solution
proposed by the bounding function, then the node is fathomed, since it is not possible to get a
lower value of the objective function at any node that descends from this one (the bounding
function has made sure of that). All that remains is to compare the solution value at the node to
the value of the incumbent, and to replace the incumbent if the current node has a lower value.
Infeasibility pruning is also worthwhile in this algorithm since it is easy to determine when a bud
node can never develop into a feasible solution, no matter how the remaining variables are set.
This is done by examining each constraint one by one. For each constraint, calculate the largest
possible left hand side value, given the decisions made so far, as follows: (left hand side value
for variables set so far) + (maximum left hand side value for variables not yet set). The second
term is obtained by assuming that a variable will be set to 0 if its coefficient is negative and 1 if
its coefficient is positive. If the largest possible left hand side value is still less than the right
hand side constant, then the constraint can never be satisfied, no matter how the remaining
variables are set, so this node can be eliminated as “impossible”. For example, consider the
constraint –4x1 – 5x2 + 2x3 + 2x4 – 3x5 1. Suppose that both x1 and x2 have already been set to
1, while the remaining variables have not yet been set. The largest possible left hand side results
if x3 and x4 are set to 1 while x5 is set to 0, giving a left hand side value of (–9) + (4) = –5, which
is not 1, hence the partial solution (1,1,?,?,?) cannot ever yield a feasible solution, so the node
is fathomed as “impossible”.
Balas Additive Algorithm uses depth-first node selection. It is of course possible to replace this
by another node selection strategy, such as best-first, but if you do so then you are no longer
following Balas’ algorithm, strictly speaking. If your problem formulation states that you are
using the Balas algorithm, then you must use depth-first node selection.
Consider the following example:
Minimize Z = 3x1 + 5x2 + 6x3 + 9x4 + 10x5 + 10x6
Subject to: (1) –2x1 + 6x2 – 3x3 + 4x4 + x5 – 2x6 2
Practical Optimization: a Gentle Introduction John W. Chinneck, 2015
2
http://www.sce.carleton.ca/faculty/chinneck/po.html
(2) –5x1 – 3x2 + x3 + 3x4 – 2x5 + x6 –2
(3) 5x1 – x2 + 4x3 – 2x4 + 2x5 – x6 3
and xj binary for j=1,2…6
Note that the variables are already ordered as required by Balas’ algorithm. There are 2 6 = 64
possible solutions if they are all enumerated, but we expect that Balas’ algorithm will generate
far fewer full and partial solutions. The branch and bound tree develops as shown in the
following diagrams. Figure 13.1 shows the root node, which has an objective function value of 0
and is infeasible by constraints 1 and 3, hence it must be
0 expanded. From here on, each node is labelled with the
All solns inf: 1,3 bounding function value, and an indication of status for the
current solution that the node represents (note that this is not
the same as the bounding function solution for zero nodes). Inf
Figure 13.1: Root node.
indicates that the node is currently infeasible and Imp indicates
that the node has been found to be impossible to satisfy; each of these notations is followed by an
indication of which constraints are causing infeasibility or impossibility.
Figure 13.2 shows the branching on x1, the first variable.
x1 0 5 Notice that if x1 is set to 1, then the bounding function
inf: 1, 3 assumes that we will not have to set any more variables to
All solns 1, hence the bounding function value is 3, since c1 = 3.
3 However, if x1 is set to 0, then at least one more variable
1 must be set to 1, and the bounding function assumes that
inf: 1, 2
the cheapest variable, x2, the next variable in the ordered
Figure 13.2: First branching.
list, is the one that will be set to 1, hence the bounding
function value is 5 because c2 = 5. The bounding function does not yield a feasible solution at
either node.
There are still live bud nodes on the
x1 0 5 developing branch and bound tree, so we
inf: 1, 3 choose the next node to expand, via the depth-
All solns first rule. Here we have just the two nodes to
x2 9 choose from, and since this is a minimization
1 0
inf: 1, 2 problem, we choose the node having the
smallest value of the bounding function, and
1 8 expand it using the next variable in the list, x2.
imp: 2 This is shown in Figure 13.3. Note that node
(1,1,?,?,?,?) is impossible by constraint 2.
Figure 13.3: Second branching.
Once x1 and x2 are set to 1, no matter how the
remaining variables are set, the left hand side will never be greater than –2
Now we select the next node for expansion. Since we are using depth-first node selection, we
are left only a single bud node to choose: (1,0,?,?,?,?), with a bounding function value of 9.
Best-first node selection would have chosen node (0,?,?,?,?,?) because it has a lower bounding
function value of 5.
Practical Optimization: a Gentle Introduction John W. Chinneck, 2015
3
http://www.sce.carleton.ca/faculty/chinneck/po.html
The expansion of node (1,0,?,?,?,?)
is shown in Figure 13.4. Node
x1 0 5 (1,0,0,?,?,?) is fathomed and found
inf: 1, 3 to be feasible when using the
All solns bounding function solution
x2 x3 (1,0,0,1,0,0), with an objective
1 0 0 12 function value of 12. This is our
fathomed
first incumbent solution. Node
9 (1,0,1,?,?,?) is found to be
1 1 impossible by constraint 1.
imp: 1
Figure 13.4: Third branching. At this point, both of the nodes just
created are not eligible for further
expansion, so we back up the tree, looking for a level at which one of the nodes is unexplored.
Figure 13.5 shows that the next branching occurs at the node (0,?,?,?,?,?).
Both child nodes are infeasible, but not
x2 0 6 impossible. The node having the lowest
x1 0 inf: 1, 3 bounding function value is chosen for
further branching, as shown in Figure
All solns 1 5
inf: 2, 3 13.6.
1 0 x3
0 12 The new zero node created has a
bounding function value of 14, worse
than the incumbent, so it is pruned
1 1 immediately, without bothering to check
feasibility or impossibility. The new one
Figure 13.5: Fourth branching. node is fathomed, and the associated
solution (0,1,1,0,0,0) has an objective
function value of 11. This is
6 lower than the previous
x2 0 inf: 1, 3
incumbent, so it becomes the new
incumbent, and the node
x1 0 x3 0 14 associated with the previous
1 11 incumbent is pruned. There is
All solns 1 still a live node that has a
fathomed
1 promising value of the bounding
0 function: (0,0,?,?,?,?), so this
0
node is expanded next, as shown
in Figure 13.7.
1 1
There is again just one node to
Figure 13.6: Fifth branching.
expand: (0,0,1,?,?,?), as shown in
Figure 13.8. Both child nodes
have bounding function values that are worse than the objective function value of the incumbent,
and so are pruned.
Practical Optimization: a Gentle Introduction John W. Chinneck, 2015
4
http://www.sce.carleton.ca/faculty/chinneck/po.html
There are no more bud nodes, so the branch and bound solution is complete and the incumbent
solution is the optimum:
0 9 (0,1,1,0,0,0) with an objective
x3 imp: 3 function value of 11.
x2 0 6 Note that we examined 15 nodes in
1
inf: 1 total, including the root node. So we
x1 0 0 did 15/64 = 23% of the work as
compared to a full enumeration.
All solns 1 1 11 This is a good reduction of effort,
but we should expect to see much
1 0 more dramatic speed-ups on larger
0 problems where early pruning cuts
off branches that could have had
1 1 numerous descendants.
Figure 13.7: Sixth branching. Balas' algorithm is just one way of
dealing with binary problems. More
general methods can also be
0 used, such as the techniques for
x3 mixed-integer programming that
x4 0 16
we will explore next.
x2 0 1
1 15 Mixed-Integer Linear
x1 0 0 Programming
All solns 1 1 11A mixed-integer programming
(MIP) problem results when
1 0 some of the variables in your
0
model are real-valued (can take
on fractional values) and some
1 1 of the variables are integer-
valued. The model is therefore
Figure 13.8: Seventh branching.
“mixed”. When the objective
function and constraints are all
linear in form, then it is a mixed-integer linear program (MILP). In common parlance, MIP is
often taken to mean MILP, though mixed-integer nonlinear programs (MINLP) also occur, and
are much harder to solve. As you will see later, MILP techniques are effective not only for
mixed problems, but also for pure-integer problems, pure-binary problems, or in fact any
combination of real-, integer-, and binary-valued variables.
Mixed-integer programs often arise in the context of what would otherwise seem to be a linear
program. However, as we saw in the previous chapter, it simply doesn’t work to treat the integer
variable as real, solve the LP, then round the integer variable to the nearest integer value. Let’s
take a look at how integer variables arise in an LP context.
Practical Optimization: a Gentle Introduction John W. Chinneck, 2015
5
http://www.sce.carleton.ca/faculty/chinneck/po.html
Either/Or Constraints
Either/or constraints arise when we have a choice between two constraints, only one of which
has to hold. For example, the metal finishing machine production limit in the Acme Bicycle
Company linear programming model is x1 + x2 4. Suppose we have a choice between using
that original metal finishing machine, or a second one that has the associated constraint x1 + 1.5x2
6. We can use either the original machine or the second one, but not both. How do we model
this situation?
An important clue lies in observing what happens if you add a large positive number (call it M)
to the right hand side of a constraint, e.g. x1 + x2 4 + M. This now says x1 + x2 “very big
number”, so any values of x1 and x2 will satisfy this constraint. In other words, the constraint is
eliminated. So what we want in our either/or example is the following:
x1 + x2 4 only this constraint holds
either
x1 + 1.5x2 6 + M
x1 + x2 4 + M
or
x1 + 1.5x2 6 only this constraint holds
We can achieve an equivalent effect by introducing a single binary variable (call it y), and using
it in two constraints, both of which are included in the model, as follows:
(1) x1 + x2 4 + My
(2) x1 + 1.5x2 6 + M(1-y)
Now if y = 0 then only constraint (1) holds, and if y = 1 then only constraint (2) holds, exactly
the kind of either/or behaviour we wanted. The downside, of course, is that a linear program has
been converted to a mixed-integer program that is harder to solve.
k out of N Constraints Must Hold
This is a generalization of the either/or situation described above. For example, we may want
any 3 out of 5 constraints to hold. This is handled by introducing N binary variables, y1...yN, one
for each constraint, as follows:
f1(x) b1 + My1
…
fN(x) bN + MyN
and including the following additional constraint:
N
i 1
yi N k
This final constraint works as follows: since we want k constraints to hold, there must be N-k
constraints that don’t hold, so this constraint insures that N-k of the binary variables take the
value 1 so that associated M values are turned on, thereby eliminating the constraint.
Practical Optimization: a Gentle Introduction John W. Chinneck, 2015
6
http://www.sce.carleton.ca/faculty/chinneck/po.html
Functions Having N Discrete Values
Sometimes you have a resource that is available in only certain discrete sizes. For example, the
metal finishing machine may be an equality that has 3 settings: x1 + x2 = 4 or 6 or 8. This can be
handled by introducing one binary variable for each of the right hand side values. Where there
are N discrete right hand sides, the model becomes:
f ( x) i 1 bi yi and
N N
i 1
yi 1
This assures that exactly one of the right hand side values is chosen. In the metal finishing
machine example, the model would be:
x1 + x2 = 4y1 + 6y2 + 8y3
y1 + y2 + y3 =1
and y1, y2, y3 binary.
Fixed Charges and Set-up Costs
Fixed charges or set-up costs are incurred when there is some kind of fixed initial cost associated
with the use of any amount of a variable, even a tiny amount. For example, if you wish to use
any amount at all of a new type of metal finishing for the ABC Company, then you incur a one-
time set-up cost for buying and installing the required new equipment. Fixed charges and set-up
costs occur frequently in practice, so it is important to be able to model them.
Mathematically speaking, a set-up charge is modelled as follows:
0 if xj = 0
f(xj) =
K + cjxj if xj > 0
where K is the fixed charge. This says that there are no charges at all if the resource represented
by xj is not used, but if it is used, then we incur both the fixed charge K and the usual charges
associated with the use of xj, represented by cjxj.
The objective function must also be modified. It becomes:
minimize Z = f(xj) + (rest of objective function)
Note the minimization: set-up costs are only interesting in the cost-minimization context. If it is
cost-maximization (a strange concept…) then we would of course always incur the set-up cost by
insuring that every resource was always used.
The final model introduces a binary variable y that determines whether or not the set-up charge is
incurred:
Minimize Z = [Ky + cjxj] + (rest of objective function)
subject to: xj – My 0
other constraints
y binary
Practical Optimization: a Gentle Introduction John W. Chinneck, 2015
7
http://www.sce.carleton.ca/faculty/chinneck/po.html
This behaves as follows. If xj > 0, then the first constraint insures that y = 1, so that the fixed
charge in the objective function is properly applied. However, if xj = 0, then y could be 0 or 1:
the first constraint is not restrictive enough in this sense. We want y to be zero in this case so
that the set-up cost is not unfairly applied, and something in the model actually does influence y
to be zero. Can you see what it is? It is the minimization objective. Given the free choice in this
case between incurring a set-up cost or not, the minimization objective will obviously choose not
to. Hence we have exactly the behaviour that we wish to model. Once again, though, we have
converted a linear program to a mixed-integer linear program.
Dakin’s Algorithm for Solving Mixed-Integer Linear Programs
Now that we’ve seen how integer or binary variables can enter linear programs, we need a
method for solving the resulting mixed-integer problems. Because of the integer or binary
variables, we will need to use some kind of branch and bound approach. Dakin’s algorithm is a
branch and bound method that uses an interesting bounding function: it simply ignores the
integer restrictions and solves the model as though all of the variables were real-valued! This
LP-relaxation provides an excellent bound on the best objective function value obtainable, and
sometimes results in a feasible solution when all of the integer variables actually get integer
values in the LP solution.
The second aspect of Dakin’s algorithm is the branching. As a node is expanded, two child
nodes are created in which new variable bounds are added to the problem. We first identify the
candidate variables: those integer variables that did not get integer values in the LP-relaxation
solution associated with the node. One of these candidate variables is chosen for branching.
Let’s consider candidate variable xj that has a non-integer value that is between the next smaller
integer k and the next larger integer k+1. The branching then creates two child nodes:
the parent node LP plus the new variable bound xj k
the parent node LP plus the new variable bound xj k+1
For example, consider some candidate variable xj that has the value 5.761. One child node will
consist of the parent LP plus the new variable bound xj 5 and the other child node will consist
of the parent LP plus the new variable bound xj 6. These new nodes force xj away from its
current non-integer value. There is no guarantee that it will get an integer value in the next LP-
relaxation, however (though this often happens).
Fathoming is simple. If the LP-relaxation at a node assigns integer values to all integer
variables, then the solution is integer-feasible, and is the best that can be attained by further
expansion of that node. The solution value is then compared to the incumbent and replaces the
incumbent if it is better. If the LP-relaxation is LP-infeasible, then the node and all of its
descendents are infeasible, and it can be pruned.
Node selection is normally depth-first. This is because a child node is exactly the same as the
parent node, except for one changed variable bound. This means that the LP basis from the
parent node LP-relaxation solution can be used as a hot start for the child node LP-relaxation. Of
course the parent node solution will definitely be infeasible in the child node, but a dual simplex
restart can be used and will very quickly iterate to a new optimum solution. This is much more
Practical Optimization: a Gentle Introduction John W. Chinneck, 2015
8
http://www.sce.carleton.ca/faculty/chinneck/po.html
efficient than, say, best-first node selection, which would
x2 require restarting LPs from scratch at most nodes.
9
Let’s look at a small example that appears in a textbook
by Winston (Mathematical Programming, 1991, p. 489):
optimum of
6 initial LP Maximize Z = 8x1 + 5x2
relaxation s.t. x1 + x2 6
9x1 + 5x2 45
x1, x2 are integer and nonnegative.
feasible A graph of this problem is shown in Figure 13.9. The
region initial LP relaxation is created when the original model,
x1 shown above, is simply treated as an LP and solved. The
5 6 LP-optimum occurs at (3.75, 2.25) with Z = 41.25.
However this is not integer-optimum since both integer
Figure 13.9: Initial LP relaxation. variables have taken on fractional values, so we must
develop a branch and bound tree following Dakin’s
algorithm.
This branch and bound tree develops as shown in Figure 13.10. Small sketches of the feasible
region for some of the LP-relaxations are also shown on the diagram. Note how the new variable
bounds gradually “square off” the LP-relaxation feasible regions until solutions are found in
which both of the integer variables indeed have integer values.
Each node in Figure 13.10 represents the solution of an LP-relaxation. Numbers indicate the
order of the solutions. An incumbent solution of (3,3) with Z = 39 is obtained early, at the
second LP solution. However there are other promising nodes with better bounding function
values, so tree development continues. A better incumbent is eventually found: node 7 with a
solution of (5,0) and Z = 40. At this point, all other nodes are pruned and the solution process
halts. Note how far the final solution of (5,0) is from the initial LP-relaxation solution of
(3.75,2.25): you can’t get to the final solution by rounding!
You will not need to set up the MILP branch and bound tree manually in practice. Most
commercial LP solvers will accept integer or binary restrictions on variables as part of their
input. They then take care of setting up the branch and bound tree automatically. As you can
imagine though, MILP solutions generally take a lot longer than identical LP solutions!
A number of further improvements on the basic algorithm are used in commercial MILP solvers:
Which candidate variable is selected for branching can have a big impact, so there are
more advanced algorithms for making this decision.
You don't normally solve the LP relaxation for both child nodes after branching. You
normally just solve the up-branch (in which the lower bound was increased), or just the
down-branch, or you use a more sophisticated algorithm for choosing the branching
direction. Depth-first search then continues without solving the LP-relaxation for the
sibling node. If needed, the search will backtrack to the sibling node eventually.
Practical Optimization: a Gentle Introduction John W. Chinneck, 2015
9
http://www.sce.carleton.ca/faculty/chinneck/po.html
A variety of sophisticated algorithms are available for choosing the next node to expand
when the depth-first search must backtrack.
The root node is subjected to intensive analysis before branch and bound begins in the
hopes of greatly reducing the subsequent amount of work.
Many other advanced techniques are also available, like probing algorithms that explore
the region around promising solutions. MILP is an active area of research!
Figure 13.10: Branch and bound tree for Dakin's algorithm.
Practical Optimization: a Gentle Introduction John W. Chinneck, 2015
10
http://www.sce.carleton.ca/faculty/chinneck/po.html
You might also like
- 15.053 February 22, 2007: Introduction To The Simplex AlgorithmNo ratings yet15.053 February 22, 2007: Introduction To The Simplex Algorithm62 pages
- Convexity Examples: CE 377K Stephen D. Boyles Spring 2015No ratings yetConvexity Examples: CE 377K Stephen D. Boyles Spring 201511 pages
- Module - 3 Lecture Notes - 5 Revised Simplex Method, Duality and Sensitivity AnalysisNo ratings yetModule - 3 Lecture Notes - 5 Revised Simplex Method, Duality and Sensitivity Analysis11 pages
- Optimization I: Brute Force and Greedy Strategy: 3.1 Heuristic Search ApproachesNo ratings yetOptimization I: Brute Force and Greedy Strategy: 3.1 Heuristic Search Approaches13 pages
- 7.6 Branch and Bound Method: C 1 1 0 0 0 Basic Variables Basic Basic Variables X X S S S Coefficient Variables ValuesNo ratings yet7.6 Branch and Bound Method: C 1 1 0 0 0 Basic Variables Basic Basic Variables X X S S S Coefficient Variables Values8 pages
- The Simplex Algorithm: Putting Linear Programs Into Standard Form Introduction To Simplex AlgorithmNo ratings yetThe Simplex Algorithm: Putting Linear Programs Into Standard Form Introduction To Simplex Algorithm25 pages
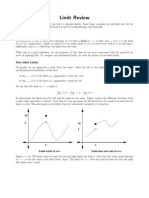
- 11 Limits of Functions of Real Variables: 11.1 The ε / δ DefinitionNo ratings yet11 Limits of Functions of Real Variables: 11.1 The ε / δ Definition7 pages
- Simplex Method - Linear Programming ProblemsNo ratings yetSimplex Method - Linear Programming Problems10 pages
- Simplex Method: Theory at A Glance (For IES, GATE, PSU) General Linear Programming ProblemNo ratings yetSimplex Method: Theory at A Glance (For IES, GATE, PSU) General Linear Programming Problem12 pages
- Additional Simplex Algorithms: Dual Simplex Method and Generalized Simplex MethodNo ratings yetAdditional Simplex Algorithms: Dual Simplex Method and Generalized Simplex Method44 pages
- Notes On Linear Programming: CE 377K Stephen D. Boyles Spring 2015No ratings yetNotes On Linear Programming: CE 377K Stephen D. Boyles Spring 201517 pages
- The Kuhn-Tucker Conditions: Minimize Such That 0 1,..., H 0 1,...No ratings yetThe Kuhn-Tucker Conditions: Minimize Such That 0 1,..., H 0 1,...11 pages
- Limits and Continuity (Calculus) Engineering Entrance Exams Question BankFrom EverandLimits and Continuity (Calculus) Engineering Entrance Exams Question BankNo ratings yet
- Student's Solutions Manual and Supplementary Materials for Econometric Analysis of Cross Section and Panel Data, second editionFrom EverandStudent's Solutions Manual and Supplementary Materials for Econometric Analysis of Cross Section and Panel Data, second editionNo ratings yet
- Exercises of Integrals and Integro-Differentials EquationsFrom EverandExercises of Integrals and Integro-Differentials EquationsNo ratings yet
- 5-Modern Liberalism & Social DemocracyNo ratings yet5-Modern Liberalism & Social Democracy15 pages
- Ee429 Programmable Logic Controllers (Dept. Elective - IV) : Course Description & ObjectivesNo ratings yetEe429 Programmable Logic Controllers (Dept. Elective - IV) : Course Description & Objectives1 page
- I. Answer The Following: 1. List The Different Rules For Sharing Computer and EquipmentNo ratings yetI. Answer The Following: 1. List The Different Rules For Sharing Computer and Equipment3 pages
- Cancelling Bill of Exchange Error If There Is A Partial PaymentNo ratings yetCancelling Bill of Exchange Error If There Is A Partial Payment2 pages
- Test Design and Automation For REST API PDFNo ratings yetTest Design and Automation For REST API PDF101 pages
- Dokument - Pub Handbookpdf Flipbook PDFNo ratings yetDokument - Pub Handbookpdf Flipbook PDF78 pages
- Implement A Verilog Model and Display The Output For A Set of Sample Data Together With The Wave Form Obtained For The Problems Given BelowNo ratings yetImplement A Verilog Model and Display The Output For A Set of Sample Data Together With The Wave Form Obtained For The Problems Given Below6 pages
- Fundamentals of Computer and Emerging TechnologiesNo ratings yetFundamentals of Computer and Emerging Technologies1 page
- International Journal of Artificial Intelligence & Applications (IJAIA)No ratings yetInternational Journal of Artificial Intelligence & Applications (IJAIA)2 pages
- GRC POST INSTALLATION - Auttomatic Workflow CustomizingNo ratings yetGRC POST INSTALLATION - Auttomatic Workflow Customizing31 pages
- Control Statements: Part 1: Let's All Move One Place OnNo ratings yetControl Statements: Part 1: Let's All Move One Place On40 pages
- A Novel Framework for Detection and Prevention of Denial of 2024 Vehicular CNo ratings yetA Novel Framework for Detection and Prevention of Denial of 2024 Vehicular C13 pages
- PS-42267-FlashSmart Product SpecificationsNo ratings yetPS-42267-FlashSmart Product Specifications16 pages
- 15.053 February 22, 2007: Introduction To The Simplex Algorithm15.053 February 22, 2007: Introduction To The Simplex Algorithm
- Convexity Examples: CE 377K Stephen D. Boyles Spring 2015Convexity Examples: CE 377K Stephen D. Boyles Spring 2015
- Module - 3 Lecture Notes - 5 Revised Simplex Method, Duality and Sensitivity AnalysisModule - 3 Lecture Notes - 5 Revised Simplex Method, Duality and Sensitivity Analysis
- Optimization I: Brute Force and Greedy Strategy: 3.1 Heuristic Search ApproachesOptimization I: Brute Force and Greedy Strategy: 3.1 Heuristic Search Approaches
- 7.6 Branch and Bound Method: C 1 1 0 0 0 Basic Variables Basic Basic Variables X X S S S Coefficient Variables Values7.6 Branch and Bound Method: C 1 1 0 0 0 Basic Variables Basic Basic Variables X X S S S Coefficient Variables Values
- The Simplex Algorithm: Putting Linear Programs Into Standard Form Introduction To Simplex AlgorithmThe Simplex Algorithm: Putting Linear Programs Into Standard Form Introduction To Simplex Algorithm
- 11 Limits of Functions of Real Variables: 11.1 The ε / δ Definition11 Limits of Functions of Real Variables: 11.1 The ε / δ Definition
- Simplex Method: Theory at A Glance (For IES, GATE, PSU) General Linear Programming ProblemSimplex Method: Theory at A Glance (For IES, GATE, PSU) General Linear Programming Problem
- Additional Simplex Algorithms: Dual Simplex Method and Generalized Simplex MethodAdditional Simplex Algorithms: Dual Simplex Method and Generalized Simplex Method
- Notes On Linear Programming: CE 377K Stephen D. Boyles Spring 2015Notes On Linear Programming: CE 377K Stephen D. Boyles Spring 2015
- The Kuhn-Tucker Conditions: Minimize Such That 0 1,..., H 0 1,...The Kuhn-Tucker Conditions: Minimize Such That 0 1,..., H 0 1,...
- Top Numerical Methods With Matlab For Beginners!From EverandTop Numerical Methods With Matlab For Beginners!
- Limits and Continuity (Calculus) Engineering Entrance Exams Question BankFrom EverandLimits and Continuity (Calculus) Engineering Entrance Exams Question Bank
- Student's Solutions Manual and Supplementary Materials for Econometric Analysis of Cross Section and Panel Data, second editionFrom EverandStudent's Solutions Manual and Supplementary Materials for Econometric Analysis of Cross Section and Panel Data, second edition
- Exercises of Integrals and Integro-Differentials EquationsFrom EverandExercises of Integrals and Integro-Differentials Equations
- Introduction to Advanced Mathematical AnalysisFrom EverandIntroduction to Advanced Mathematical Analysis
- Ee429 Programmable Logic Controllers (Dept. Elective - IV) : Course Description & ObjectivesEe429 Programmable Logic Controllers (Dept. Elective - IV) : Course Description & Objectives
- I. Answer The Following: 1. List The Different Rules For Sharing Computer and EquipmentI. Answer The Following: 1. List The Different Rules For Sharing Computer and Equipment
- Cancelling Bill of Exchange Error If There Is A Partial PaymentCancelling Bill of Exchange Error If There Is A Partial Payment
- Implement A Verilog Model and Display The Output For A Set of Sample Data Together With The Wave Form Obtained For The Problems Given BelowImplement A Verilog Model and Display The Output For A Set of Sample Data Together With The Wave Form Obtained For The Problems Given Below
- Fundamentals of Computer and Emerging TechnologiesFundamentals of Computer and Emerging Technologies
- International Journal of Artificial Intelligence & Applications (IJAIA)International Journal of Artificial Intelligence & Applications (IJAIA)
- GRC POST INSTALLATION - Auttomatic Workflow CustomizingGRC POST INSTALLATION - Auttomatic Workflow Customizing
- Control Statements: Part 1: Let's All Move One Place OnControl Statements: Part 1: Let's All Move One Place On
- A Novel Framework for Detection and Prevention of Denial of 2024 Vehicular CA Novel Framework for Detection and Prevention of Denial of 2024 Vehicular C