0 ratings0% found this document useful (0 votes)
10 viewsModule 2 ppt
Uploaded by
devpanwar2907Copyright
© © All Rights Reserved
Available Formats
Download as PDF, TXT or read online on Scribd
0 ratings0% found this document useful (0 votes)
10 viewsModule 2 ppt
Uploaded by
devpanwar2907Copyright
© © All Rights Reserved
Available Formats
Download as PDF, TXT or read online on Scribd
You are on page 1/ 18
MODULE 2
• What is Fuzzy Set ?
• Fuzzy refers to something that is unclear or
vague .
• Hence, Fuzzy Set is a Set where every key is
associated with value, which is between 0 to 1
based on the certainty .
• This value is often called as degree of
membership. Fuzzy Set is denoted with a Tilde
Sign on top of the normal Set notation.
• Operations on Fuzzy Set with Code :
• 1. Union :
• Consider 2 Fuzzy Sets denoted by A and B,
then let’s consider Y be the Union of them,
then for every member of A and B, Y will be:
• degree_of_membership(Y)=
max(degree_of_membership(A),
degree_of_membership(B))
• The First Fuzzy Set is : {'a': 0.2, 'b': 0.3, 'c': 0.6, 'd': 0.6}
• The Second Fuzzy Set is : {'a': 0.9, 'b': 0.9, 'c': 0.4, 'd': 0.5}
• Fuzzy Set Union is : {'a': 0.9, 'b': 0.9, 'c': 0.6, 'd': 0.6}
• 2. Intersection :
• Consider 2 Fuzzy Sets denoted by A and B,
then let’s consider Y be the Intersection of
them, then for every member of A and B, Y
will be:
• degree_of_membership(Y)=
min(degree_of_membership(A),
degree_of_membership(B))
• EXAMPLE :
• The First Fuzzy Set is : {'a': 0.2, 'b': 0.3, 'c': 0.6, 'd': 0.6}
• The Second Fuzzy Set is : {'a': 0.9, 'b': 0.9, 'c': 0.4, 'd': 0.5}
• Fuzzy Set Intersection is : {'a': 0.2, 'b': 0.3, 'c': 0.4, 'd': 0.5}
• 3. Complement :
• Consider a Fuzzy Sets denoted by A , then let’s
consider Y be the Complement of it, then for
every member of A , Y will be:
• degree_of_membership(Y)= 1 -
degree_of_membership(A)
• The Fuzzy Set is : {'a': 0.2, 'b': 0.3, 'c': 0.6, 'd': 0.6}
• Fuzzy Set Complement is : {'a': 0.8, 'b': 0.7, 'c': 0.4,
'd': 0.4}
• 4. Difference :
Consider 2 Fuzzy Sets denoted by A and B, then
let’s consider Y be the Intersection of them, then
for every member of A and B, Y will be:
• degree_of_membership(Y)=
{min(degree_of_membership(A), 1-
degree_of_membership(B)}
• EXAMPLE :
• The First Fuzzy Set is : {"a": 0.2, "b": 0.3, "c": 0.6, "d": 0.6}
• The Second Fuzzy Set is : {"a": 0.9, "b": 0.9, "c": 0.4, "d": 0.5}
• Fuzzy Set Difference is : {"a": 0.1, "b": 0.1, "c": 0.6, "d": 0.5}
• SELECTION OF MEMBERSHIP FUNCTION
• To be frank, there are no hard and fast rules about the
selection of membership functions because it really
depends on the applications where the fuzzy systems
are to be implemented.
• These applications can be generally classified using a
mnemonic acronym that I called, “Fuzzy D.I.S.C.”
• Decision Maker (e.g., Multiple-criteria decision analysis)
• Identifier (e.g., System identification)
• Scheduler (e.g., Machine scheduling)
• Controller (e.g., Adaptive & supervisory control of
nonlinear systems)
• The way a membership function is selected largely
depends on how we quantify the certainty (degree
of truth) of an input space according to our self-
defined meaning of the linguistic values (Big /
Small, High / Low, Positive / Negative, Average /
Medium, etc.) together with the quantifiers (very,
mostly, much, few, little, not).
• In control applications, we often start with
quantifying the input space using rectilinear
membership functions (e.g. triangular and
trapezoidal) and then gradually replacing them with
curvilinear membership functions (e.g. gaussMF,
gbellMF, etc.) until a desired response is achieved.
• It is important to note that for the most part
the selection of a membership function is
subjective rather than objective.
• That is, we simply quantify it on a basis that
makes sense to us, but others may view it
differently and quantify it using other type of
membership functions.
Fuzzy Logic Control System
• Fuzzy logic control (FLC) is the most active research
area in the application of fuzzy set theory, fuzzy
reasoning, and fuzzy logic.
• The application of FLC extends from industrial
process control to biomedical instrumentation and
securities.
• Compared to conventional control techniques, FLC
has been best utilized in complex ill-defined
problems, which can be controlled by an efficient
human operator without knowledge of their
underlying dynamics.
What is fuzzy rule?
Fuzzy rules are an integral component of fuzzy
logic, an approach that seeks to emulate the way
humans make decisions.
At its core, a fuzzy rule deals with imprecise
information and is a part of fuzzy logic systems,
enabling decision-making based on approximate
reasoning rather than precise input.
The fundamental premise of a fuzzy rule lies in
assigning membership degrees to variables,
allowing for the expression of linguistic
relationships.
• The definition of fuzzy rule in the ai context
• Within the AI context, fuzzy rules play a vital
role in enhancing decision-making processes.
They enable AI systems to handle complex,
imprecise, or uncertain input data by
introducing a layer of abstraction.
• This abstraction facilitates more human-like
decision-making, making AI systems proficient
in scenarios where precise or binary logic may
fall short, such as in natural language
understanding or perceptual reasoning tasks.
• Real-world examples and applications
• Example 1: fuzzy rule in autonomous vehicles
• In the context of autonomous vehicles, fuzzy
rules are employed to make critical decisions
related to navigation, obstacle avoidance, and
speed regulation.
• By integrating fuzzy rules into the vehicle's
control system, it can effectively interpret and
respond to real-time environmental cues,
enhancing the safety and efficiency of
autonomous navigation.
• Example 2: fuzzy rule in medical diagnosis
systems
• Medical diagnosis systems leverage fuzzy
rules to process intricate diagnostic criteria and
patient data, leading to precise and context-
aware diagnoses.
• By incorporating fuzzy rules, these systems can
navigate through complex medical conditions,
identifying patterns and correlations that may
not be immediately discernible through
traditional analytic approaches.
• Example 3: fuzzy rule in smart home
technology
• In the realm of smart home technology, fuzzy
rules are applied to intelligently manage
energy consumption, optimize climate control,
and automate routine tasks.
• This application enables smart home systems
to adapt to user preferences, environmental
conditions, and occupancy patterns, creating a
seamless and personalized living experience.
• Fuzzification:
• It is the method of transforming a crisp quantity(set) into
a fuzzy quantity(set).
• This can be achieved by identifying the various known
crisp and deterministic quantities as completely
nondeterministic and quite uncertain in nature.
• This uncertainty may have emerged because of vagueness
and imprecision which then lead the variables to be
represented by a membership function as they can be
fuzzy in nature.
• For example, when I say the temperature is 45° Celsius the
viewer converts the crisp input value into a linguistic
variable like favorable temperature for the human body,
hot or cold.
• Defuzzification: It is the inverse of fuzzification.
The former one was used to convert the crisp
results into fuzzy results but here the mapping is
done to convert the fuzzy results into crisp results.
• This process is capable of generating a non-fuzzy
control action which illustrates the possibility
distribution of an inferred fuzzy control action.
Defuzzification process can also be treated as the
rounding off process, where fuzzy set having a
group of membership values on the unit interval
reduced to a single scalar quantity.
S.No. Comparison Fuzzification Defuzzification
Precise data is converted into Imprecise data is converted into
1. Basic
imprecise data. precise data.
Defuzzification is the inverse process
Fuzzification is the method of
of fuzzification where the mapping is
2. Definition converting a crisp quantity into a
done to convert the fuzzy results
fuzzy quantity.
into crisp results.
Like, Stepper motor and D/A
3. Example Like, Voltmeter
converter
Intuition, inference, rank ordering, Maximum membership principle,
4. Methods angular fuzzy sets, neural network, centroid method, weighted average
etcetera. method, center of sums, etcetera.
5. Complexity It is quite simple. It is quite complicated.
It can use IF-THEN rules for fuzzifying It uses the center of gravity methods
6. Use
the crisp value. to find the centroid of the sets.
You might also like
- Fuzzy Logic: Presented by Wei Zhang CSE Dept. Lehigh UniversityNo ratings yetFuzzy Logic: Presented by Wei Zhang CSE Dept. Lehigh University35 pages
- Fuzzy Logic: UIET (Computer Science Deptt)100% (1)Fuzzy Logic: UIET (Computer Science Deptt)56 pages
- Microsoft PowerPoint - Fuzzy Lecture-01.Ppt (Compatibility Mode)100% (1)Microsoft PowerPoint - Fuzzy Lecture-01.Ppt (Compatibility Mode)61 pages
- Fuzzy Sets and Fuzzification: Prof. Dr. Allaeldin H. KassamNo ratings yetFuzzy Sets and Fuzzification: Prof. Dr. Allaeldin H. Kassam95 pages
- Fuzzy Set Theory: Classical Set:-A Classical Set "A" Is A CollectionNo ratings yetFuzzy Set Theory: Classical Set:-A Classical Set "A" Is A Collection71 pages
- Practical 7 Introduction To Fuzzy LogicNo ratings yetPractical 7 Introduction To Fuzzy Logic20 pages
- Fuzzy Logic Control Method For The Washing Time of The Washing Machine Final Project ReportNo ratings yetFuzzy Logic Control Method For The Washing Time of The Washing Machine Final Project Report20 pages
- Uzzy Ogic: Amit Raj Satyal Bigyan Sapkota Krishna Paudyal Simon Shrestha Subash Paudyal 14 February 2012No ratings yetUzzy Ogic: Amit Raj Satyal Bigyan Sapkota Krishna Paudyal Simon Shrestha Subash Paudyal 14 February 201254 pages
- Copy of Copy of SSG 311_Module 4_Fuzzy Sets and Fuzzy Logic (1)No ratings yetCopy of Copy of SSG 311_Module 4_Fuzzy Sets and Fuzzy Logic (1)70 pages
- Scale Invariant Feature Transform: Unveiling the Power of Scale Invariant Feature Transform in Computer VisionFrom EverandScale Invariant Feature Transform: Unveiling the Power of Scale Invariant Feature Transform in Computer VisionNo ratings yet
- Active Contour: Advancing Computer Vision with Active Contour TechniquesFrom EverandActive Contour: Advancing Computer Vision with Active Contour TechniquesNo ratings yet
- Motor Feeder Cable & Cable Tray Sizing and DataNo ratings yetMotor Feeder Cable & Cable Tray Sizing and Data5 pages
- Mechanical Sample Book PDF For Gate Exam PDFNo ratings yetMechanical Sample Book PDF For Gate Exam PDF28 pages
- Comparative Stdy of Wind Analysis of Different Plan Configuration Building Using ETabsNo ratings yetComparative Stdy of Wind Analysis of Different Plan Configuration Building Using ETabs18 pages
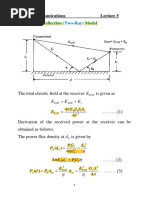
- 4.6 Ground Reflection (Two-Ray) Model: Mobile Communications Lecture 5No ratings yet4.6 Ground Reflection (Two-Ray) Model: Mobile Communications Lecture 54 pages
- Lecture 3 - Pressure of Concrete On FormworkNo ratings yetLecture 3 - Pressure of Concrete On Formwork49 pages
- IOM Presnetation GCT, Mianwali 30-01-2019 2100% (2)IOM Presnetation GCT, Mianwali 30-01-2019 242 pages
- Akash Karia - TED Talks Storytelling - 23 Storytelling Techniques From The Best TED Talks-CreateSpace Independent Publishing Platform (2015)No ratings yetAkash Karia - TED Talks Storytelling - 23 Storytelling Techniques From The Best TED Talks-CreateSpace Independent Publishing Platform (2015)40 pages
- ME3493 MANUFACTURING TECHNOLOGY syllabusNo ratings yetME3493 MANUFACTURING TECHNOLOGY syllabus2 pages
- Acoustical Board Product Data Sheet: DescriptionNo ratings yetAcoustical Board Product Data Sheet: Description2 pages
- 22.electromotive Force and Potential DifferenceNo ratings yet22.electromotive Force and Potential Difference4 pages
- Alarm List of Waukesha Generator Protection System BE1-IPS100No ratings yetAlarm List of Waukesha Generator Protection System BE1-IPS1001 page
- Proposal Sponsorship Xendit Conference 2024No ratings yetProposal Sponsorship Xendit Conference 202430 pages
- KD.3.1 How To Introduce Yourself in EnglishNo ratings yetKD.3.1 How To Introduce Yourself in English13 pages
- Fuzzy Logic: Presented by Wei Zhang CSE Dept. Lehigh UniversityFuzzy Logic: Presented by Wei Zhang CSE Dept. Lehigh University
- Microsoft PowerPoint - Fuzzy Lecture-01.Ppt (Compatibility Mode)Microsoft PowerPoint - Fuzzy Lecture-01.Ppt (Compatibility Mode)
- Fuzzy Sets and Fuzzification: Prof. Dr. Allaeldin H. KassamFuzzy Sets and Fuzzification: Prof. Dr. Allaeldin H. Kassam
- Fuzzy Set Theory: Classical Set:-A Classical Set "A" Is A CollectionFuzzy Set Theory: Classical Set:-A Classical Set "A" Is A Collection
- Fuzzy Logic Control Method For The Washing Time of The Washing Machine Final Project ReportFuzzy Logic Control Method For The Washing Time of The Washing Machine Final Project Report
- Uzzy Ogic: Amit Raj Satyal Bigyan Sapkota Krishna Paudyal Simon Shrestha Subash Paudyal 14 February 2012Uzzy Ogic: Amit Raj Satyal Bigyan Sapkota Krishna Paudyal Simon Shrestha Subash Paudyal 14 February 2012
- Copy of Copy of SSG 311_Module 4_Fuzzy Sets and Fuzzy Logic (1)Copy of Copy of SSG 311_Module 4_Fuzzy Sets and Fuzzy Logic (1)
- Soft Computing: Fundamentals and ApplicationsFrom EverandSoft Computing: Fundamentals and Applications
- Scale Invariant Feature Transform: Unveiling the Power of Scale Invariant Feature Transform in Computer VisionFrom EverandScale Invariant Feature Transform: Unveiling the Power of Scale Invariant Feature Transform in Computer Vision
- Active Contour: Advancing Computer Vision with Active Contour TechniquesFrom EverandActive Contour: Advancing Computer Vision with Active Contour Techniques
- Comparative Stdy of Wind Analysis of Different Plan Configuration Building Using ETabsComparative Stdy of Wind Analysis of Different Plan Configuration Building Using ETabs
- 4.6 Ground Reflection (Two-Ray) Model: Mobile Communications Lecture 54.6 Ground Reflection (Two-Ray) Model: Mobile Communications Lecture 5
- Akash Karia - TED Talks Storytelling - 23 Storytelling Techniques From The Best TED Talks-CreateSpace Independent Publishing Platform (2015)Akash Karia - TED Talks Storytelling - 23 Storytelling Techniques From The Best TED Talks-CreateSpace Independent Publishing Platform (2015)
- Alarm List of Waukesha Generator Protection System BE1-IPS100Alarm List of Waukesha Generator Protection System BE1-IPS100