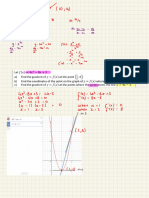
fectron 5 2

Q3 .
4

consider the graph of f(x) =

12-6x on the interval [0 3] ,

confirm the shaded region is .

9

(12-6x)dx =
9
:/(12)
Y
-

E(((6)
↓

III
12 3
(12x
-

= 9v
-

3x2)dx =
4

12(3) -

3(3)
...I
(-

36 -

27 = 9

, (2 (0) -
3/0)" = 0

9 + 0 =
9

Q3 .
7
determine the off(x) according
and to

geometre shapes
.

f(x) dx =
(i)(2) +
E(((z) =
4

,,
2 + 2

S. f(x)dx =
(1) + (1)(3) + =(2)(3) =
10

,
7 + 3
I

, ( f(x)dx =
z(z)(3) =
-
3

!. f(x)dx = 10 -
3 -

=(3 2)(2) + =
2

10-3 -
5

flat
Q3 12
S, f(t)d +
.

interal [2 07
F(x) = on ,

what value is
largest ?

# (0) (1) (2) F (3) F(M)

-camea-f22(0) Vi2(1)d
F ,
# , ,
,

df
~
-
+

O 2
<
the
F(2) is
largest value because it

/
equals zero
which is the highest .
value

All the other outputs a re

negative
because of the domain's integral property
takes
03 F(0)d F(l) The
graph
[2 for
.

of F(3) & F(4).

negative
a re a
a

F(2) doesn't it has

id
more so an a re a
,

of zero
.