Location via proxy:   [ UP ]  
[Report a bug]   [Manage cookies]                
Scribd
Upload
3 views

Lab 34 (a)

The document outlines a lab activity focused on finding areas enclosed by curves using definite integrals. It includes procedures for calculating areas under specific functions, creating input boxes for functions, and completing tables with results. The lab emphasizes understanding the area above and below the x-axis through various examples and questions.

Uploaded by

jaseenanavas4242
Copyright
© © All Rights Reserved
Available Formats
Download as PDF, TXT or read online on Scribd
3 views

Lab 34 (a)

The document outlines a lab activity focused on finding areas enclosed by curves using definite integrals. It includes procedures for calculating areas under specific functions, creating input boxes for functions, and completing tables with results. The lab emphasizes understanding the area above and below the x-axis through various examples and questions.

Uploaded by

jaseenanavas4242
Copyright
© © All Rights Reserved
Available Formats
Download as PDF, TXT or read online on Scribd
You are on page 1/ 2

Lab 34 : Application of integrals

Aim :
• To find the area enclosed by curves using definite integrals .

Concepts :
• Definite integrals.
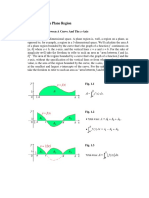
Activity 34.1 : Area bounded by x axis
Procedure :
1. Draw the graph of the function f(x) = x 2
Qn.(1). Find the area enclosed by the curve y = f(x), x axis, x = 0 and x = 2 using
the input command Integral (f ,0 ,2)
Qn.(2). Find the area enclosed by the curve y = x 2 , x axis, between
(i) x = −1 and x = 3 (ii) x = −5 and x = 0

2. Create an Input Box for the function f(x).


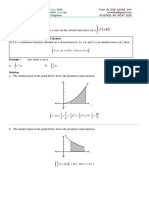
Qn.(3). Find the area enclosed by the curve y = x 2 − 1, x axis between x = −1
and x = 1.
Qn.(4). Find the required area and complete the following table.
Sl.No. Enclosed Region Area
1 y 2 = x, x axis, x = 1, x = 4 4.67
2 𝑥2 𝑦2 37.70
+ =1
16 9

3 x2 + y2 = 4 12.566
4 y = sin x, x axis, x = π, x = 2π 2
Activity 34.2 Area of a region which is above and below x axis
Procedure :
1. Set f(x) = x 2 − 3 and edit the upper and lower limits.
3
Qn.(1). What is the value of ∫−3 𝑥 2 − 3 𝑑𝑥 . Give the reason.

Qn.(2). What is the area of the portion below the x axis?


Qn.(3). What is the area of the portion above the x axis?
Qn.(4). Find the total area of the region.
Qn.(5). Find the required area and complete the following table.
Sl.No. Enclosed Region Area
1 y = sin x, x axis, x = 0, x = 2π 4
2 y = x3, x axis, x = -2, x = 4 68
3 y = |𝑥 | − 2, x axis, x = -1 , x = 3 4
4 y = 3x+2, x axis, x = -1, x = 1 4.33

You might also like