Regression Corr

Simple Linear Regression & Correlation
We now consider bivariate data. Bivariate data is data

connecting two variables:
The independent or explanatory variable, and
The dependent or response variable.
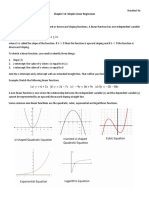
A scatter diagram is used to display bivariate data.
We are interested if there is a linear relationship between
the two sets of data displayed. This can fall in one of 3
classes:
1. POSITIVE LINEAR CORRELATION
2. NEGATIVE LINEAR CORRELATION
3. NO LINEAR CORRELATION
Scatter diagrams show plots of ordered pairs .

Usually, represents the independent variable and
represents the dependent variable. The following
scatter diagrams show different classes of linear
relationships:
x
y
( )
, x y
Graph showing positive correlation
Graph showing negative correlation
Graph showing no linear correlation
A scatter diagram is a good indication as to whether the
linear relationship between the two sets of data can be
represented by a mathematical equation.
This mathematical equation is called a regression function.
We can determine the equation of the regression line
representing the proposed relationship.
The least squares regression line of on :
The general equation of a straight line is
where represents the gradient and represents the
y-intercept. The regression equation is very similar:
The regression equation takes the form
where will represent the gradient and will represent the
y-intercept. These values are called the regression coefficients.
y
y mx c = +
x
c
m
y a bx = +
a
b
These values for and are determined by the following
formulae: and

where and are the mean of and the mean of
respectively. The formula for is based on the fact that
MUST be a point on the regression line.
N.B. and

( )
2
2
n xy x y
b
n x x

a y bx =
a
b
x
y
x
y
( )
, x y
a
n
x
x

=
n
y
y

=
A way to measure the strength of a linear relationship between two
variables is using the product moment correlation coefficient.
This is a number which lies between -1 and +1. Consider 3 cases:
If then there is positive linear correlation.
If then there is negative linear correlation.
If then there is no linear correlation present

r
0 r >
0 r =
0 r <
The correlation coefficient is calculated using the formula:

From this formula we can also determine the coefficient of determination:

This measure represents the ratio of explained variation to total variation.

( ) ( )
2 2
2 2
nxy xy
r
nx xny y
=
( (

( (

( ) ( )
2
2
2 2
2 2
nxy xy
cdr
nx x ny y
(
(
==
(
( ( (

( (
(

*A Practical Example
Tabulated is the maintenance cost/00s$ to the age/mths of 10 X-ray machines.

i. Find the least squares regression line of maintenance cost on age and use it to
predict the maintenance cost for a similar machine 40 mths old.
ii. Calculate the product moment correlation coefficient between the age of the
machine and the cost for maintenance.
iii. Determine the percentage variation in the total maintenance cost that is explained
by the variation in the machine age.
Question adapted from Business Mathematics & Statistics
395 350 300 300 335 310 300 250 240 190 Cost ( y )
60 50 50 30 30 30 20 15 10 5 Age ( x )
10 9 8 7 6 5 4 3 2 1 Machine
156025 3600 23700 395 60
122500 2500 17500 350 50
90000 2500 15000 300 50
90000 900 9000 300 30
112225 900 10050 335 30
96100 900 9300 310 30
90000 400 6000 300 20
62500 225 3750 250 15
57600 100 2400 240 10
36100 25 950 190 5
x
y
xy
2
x
2
y
300 x=
2970 y=
97650 xy=
2
12050 x =
2
913050 y=
From the table on the previous slide we know that:

i. Using the formulae from slide 9

The regression equation is
Estimated cost =

2 2
10;300;2970; 97650;12050; 913050 nxyxy x y ======
( )
2 2
2
10976503002970
2.8
1012050300
2970 300
2.8 212.9
10 10
nxy xy
b
nx x
y x
aybx b
n n

= = =

| |
== = =
|
\ .
212.9 2.8 y x = + y a bx = +
( )
212.92.840$324.90 y= +=
Recall

Using the formulae from slide 11
i. The correlation coefficient =

i. The coefficient of determination =
Thus 77% of the variation in maintenance costs is explained by the variation in
machine ages.

2 2
10;300;2970; 97650;12050; 913050 nxyxy x y ======
( ) ( )
2 2
2 2
2 2
10976503002970
1012050300 109130502970
0.88
n xy x y
r
n x x n y y
r
r
=
( (

( (

=

=

( )
2
2
0.88 0.77 cdr == =

Regression Corr

Uploaded by

Copyright:

Available Formats

Regression Corr

Uploaded by

Document Information

Copyright

Available Formats

Share this document

Share or Embed Document

Sharing Options

Did you find this document useful?

Is this content inappropriate?

Copyright:

Available Formats

Regression Corr

Uploaded by

Copyright:

Available Formats

Simple Linear Regression & Correlation

We now consider bivariate data. Bivariate data is data

From the table on the previous slide we know that:

You might also like