Extension of a local linear controller to a stabilizing semi-global piecewise affine controller
- 1. Extension of a local linear controller to a stabilizing semi-global piecewise affine controller Behzad Samadi and Luis Rodrigues Hybrid Control Systems Laboratory Department of Mechanical and Industrial Engineering Concordia University Montreal, Canada Extension of a local linear controller to a stabilizing semi-global piecewise affine controller – p. 1/14
- 2. Outline Introduction Extension of a local linear controller to a stabilizing semi-global piecewise affine controller – p. 2/14
- 3. Outline Introduction Piecewise affine approximation Extension of a local linear controller to a stabilizing semi-global piecewise affine controller – p. 2/14
- 4. Outline Introduction Piecewise affine approximation Piecewise affine controller design Extension of a local linear controller to a stabilizing semi-global piecewise affine controller – p. 2/14
- 5. Outline Introduction Piecewise affine approximation Piecewise affine controller design Example Extension of a local linear controller to a stabilizing semi-global piecewise affine controller – p. 2/14
- 6. Outline Introduction Piecewise affine approximation Piecewise affine controller design Example Conclusion Extension of a local linear controller to a stabilizing semi-global piecewise affine controller – p. 2/14
- 7. Introduction The class of nonlinear systems considered in this work is described by ˙x = Ax + a + f(x) + Bu where: x ∈ Rn is the state vector u ∈ Rm is the control input f(x) ∈ Rn is a vector function A ∈ Rn×n, a ∈ Rn, B ∈ Rn×m Extension of a local linear controller to a stabilizing semi-global piecewise affine controller – p. 3/14
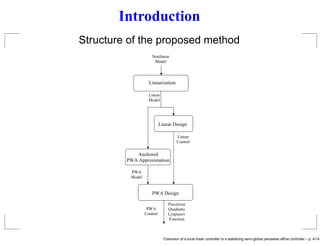
- 8. Introduction Structure of the proposed method Linear Design PWA Design Linearization Nonlinear Model Linear Model PWA Model Linear Control Piecewise Quadratic Lyapunov Function PWA Control Anchored PWA Approximation Extension of a local linear controller to a stabilizing semi-global piecewise affine controller – p. 4/14
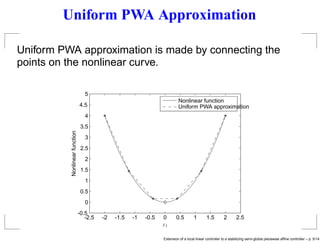
- 9. Uniform PWA Approximation Uniform PWA approximation is made by connecting the points on the nonlinear curve. x1 Nonlinearfunction Nonlinear function Uniform PWA approximation -2.5 -2 -1.5 -1 -0.5 0 0.5 1 1.5 2 2.5 -0.5 0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5 Extension of a local linear controller to a stabilizing semi-global piecewise affine controller – p. 5/14
- 10. Anchored Uniform PWA Approximation Anchored uniform PWA approximation is computed by minimizing the approximation error subject to the condition that the approximation coincides with the linear approximation at the desired point. x1 Nonlinearfunction Nonlinear function Anchored PWA approximation -2.5 -2 -1.5 -1 -0.5 0 0.5 1 1.5 2 2.5 -0.5 0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5 Extension of a local linear controller to a stabilizing semi-global piecewise affine controller – p. 6/14
- 11. PWA system Nonlinear system ˙x = Ax + a + f(x) + Bu PWA approximation of the nonlinear function ˆfPWA(x) = Af i x + af i , if x ∈ Ri To compute a PWA approximation of the nonlinear system, f(x) is replaced by ˆfPWA(x) ˙x(t) = Aix(t) + ai + Biu(t), if x(t) ∈ Ri where Ai = A + Af i , ai = a + af i Extension of a local linear controller to a stabilizing semi-global piecewise affine controller – p. 7/14
- 12. Controller Synthesis Lyapunov based approach to stabilizing a nonlinear system Lyapunov function (energy-like function) V (x) = ¯xT ¯Pi¯x, x ∈ Ri with ¯x and ¯Pi defined as ¯x = x 1 , ¯Pi ≡ Pi −Pixcl −xT clPT i ri , Pi = PT i > 0 Controller u = ¯Ki¯x, x ∈ Ri Extension of a local linear controller to a stabilizing semi-global piecewise affine controller – p. 8/14
- 13. Controller Synthesis Problem Problem constraints Continuous Lyapunov function (Equality) Positive definite Lyapunov function (LMI) Decreasing over time Lyapunov function (BMI) Continuous controller (Equality) Extension of a local linear controller to a stabilizing semi-global piecewise affine controller – p. 9/14
- 14. Example Nonlinear system ˙x1 ˙x2 = x2 + x2 1 u LQR controller parameters Q = 2 0 0 1 , R = 0.1 LQR controller for the linear approximation at x = 0 KLQR = −4.4721 −4.3525 Extension of a local linear controller to a stabilizing semi-global piecewise affine controller – p. 10/14
- 15. Example PWA controller ¯K1 = 5.9824 −4.3525 18.7150 ¯K2 = −12.1841 −4.3525 −3.0848 ¯K3 = −4.4721 −4.3525 0 ¯K4 = −8.7094 −4.3525 1.6949 ¯K5 = −22.3134 −4.3525 18.0198 Control gain for the center region ¯K3 = KLQR 0 Extension of a local linear controller to a stabilizing semi-global piecewise affine controller – p. 11/14
- 16. LQR Controller Trajectories of the nonlinear system with LQR controller x2 x1 -2 -1.5 -1 -0.5 0 0.5 1 1.5 2 -6 -4 -2 0 2 4 6 Extension of a local linear controller to a stabilizing semi-global piecewise affine controller – p. 12/14
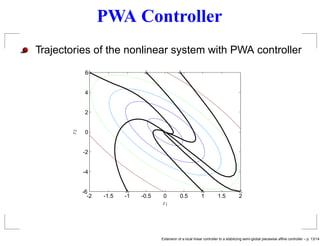
- 17. PWA Controller Trajectories of the nonlinear system with PWA controller x2 x1 -2 -1.5 -1 -0.5 0 0.5 1 1.5 2 -6 -4 -2 0 2 4 6 Extension of a local linear controller to a stabilizing semi-global piecewise affine controller – p. 13/14
- 18. Conclusion A Lyapunov-based method was proposed to extend a linear controller to a PWA controller. This addresses the problem of designing a nonlinear controller with good local performance and a large region of attraction. An optimization method was proposed to compute a PWA approximation of a nonlinear system which is identical to the linear approximation of the nonlinear system at a desired point. This helps to make PWA controller synthesis feasible in cases where the problem was not feasible because of the uniform PWA approximation error at the closed-loop equilibrium point. Extension of a local linear controller to a stabilizing semi-global piecewise affine controller – p. 14/14