[重要なお知らせ (2023/8/12)] 現在，スライドの p.10 に不十分な記述があります．ルートの答えは 0 以上の数に限定することに注意してください (たとえば -3 を 2 乗しても 9 ですが，ルート 9 は -3 ではありません)．なお，現在筆者のパソコンが修理中でデータがないので，修…
絞り込み
-
検索対象
-
ブックマーク数
-
期間
-
セーフサーチ
Mathematicsの検索結果1 - 40 件 / 559件
Mathematicsに関するエントリは559件あります。 数学、
math、
学習
などが関連タグです。 人気エントリには 『150 分で学ぶ高校数学の基礎』などがあります。
Mathematicsの関連エントリー
-
150 分で学ぶ高校数学の基礎
- 3481 users
- speakerdeck.com/e869120
- 学び
- 2022/09/07
-
コグニカル
- 3381 users
- cognicull.com
- 学び
- 2020/09/29
コグニカルは、足りない知識を掘り下げて理解する学習サイトです。
-
高校レベルの数学から大学の教養数学くらいまでを独学/学び直した - razokulover publog
- 2125 users
- razokulover.hateblo.jp
- 学び
- 2020/03/07
去年の12月頃から数学の学び直しを始めた。 職業柄少し専門的な、特に機械学習の方面の書籍などに手を出し始めると数式からは逃れられなかったりする。とはいえ元々自分は高校時代は文系で数学1A2Bまでしか履修していない。そのせいか少し数学へ苦手意識があり「図でわかるOO」とか「数学無しでもわかるOO」のような直感的に理解出来る解説に逃げることが多かった。実務上はそれで問題ないにしてもこのまま厳密な理解から逃げているのも良くないなと感じたのでもう少し先の数学に取り掛かることにした。 巷には数学の学び直しについての記事が既にたくさんある。それに自分の場合は何かの受験に成功した！とか難関の資格を取得した！というような華々しい結末を迎えている状態ではない。そんな中で自分が何か書いて誰の役にたつかもわからないが、少なくとも自分と似たようなバックグランドを持つ人には意味のある内容になるかもしれないので、どの
-
その誕生を地元新聞も経済新聞も記事にしなかった。２年後、『コードの情報を白黒の点の組み合わせに置き換える』と最下段のベタ記事で初めて紹介された時、その形を思い浮かべることができる読者はいなかった。いま、説明の必要すらない。ＱＲコードはなぜ開発され、どう動くのだろうか。 ＱＲコードは、自動車生産ラインの切実な要請と非自動車部門の技術者の「世界標準の発明をしたい」という野心の微妙な混交の下、1990年代前半の日本電装（現デンソー）で開発された。 トヨタグループの生産現場では、部品名と数量の記された物理的なカンバンが発注書、納品書として行き来することで在庫を管理する。そのデータ入力を自動化するバーコード（ＮＤコード）を開発したのがデンソーだ。 バブル全盛の1990年ごろ、空前の生産台数、多様な車種・オプションに応えるため、部品も納入業者も急激に増え、ＮＤコードが限界を迎えていた。63桁の数字しか
-
えるエル on Twitter: "東大が無償でPDF公開している，統計学会の75周年記念出版『21世紀の統計科学』の3冊 1と2は実際の統計データを用いて，各事例への統計学の応用手法，3は機械学習の人なら馴染み深い統計計算を解説 下手な市販の本を買うよりは，この3… https://t.co/w2cSVIxmUI"
- 1792 users
- twitter.com/ImAI_Eruel
- テクノロジー
- 2019/12/25
東大が無償でPDF公開している，統計学会の75周年記念出版『21世紀の統計科学』の3冊 1と2は実際の統計データを用いて，各事例への統計学の応用手法，3は機械学習の人なら馴染み深い統計計算を解説 下手な市販の本を買うよりは，この3… https://t.co/w2cSVIxmUI
-
役立つYouTubeのチャンネルまとめ 数学、物理、アルゴリズム、プログラミング、などなど自分が使う技術に役立ちそうだな、困ったときによく見たなと思うチャンネルを紹介する。 取っ掛かり、ハマりがち、コツみたいな物が拾える。数学がメイン。随時更新していくつもり。 当たり前だけどちゃんと本も読んで勉強するんだぞ。 背景 YouTubeは視聴する登録チャンネルの数が増えると、チャンネルが埋もれて発掘困難になりがち (chrome拡張でできるチャンネルのフォルダ分け機能は、ぽちぽち登録するのも面倒で、そのフォルダの中から掘り出すのも難しい) モチベが上がる(おべんつよしたい)チャンネルを探してるうちに湧いてくる、わんにゃんコンテンツ(だいちゅき)に流され一日が終わるため、 モチベが上がる有用なチャンネルにすぐにたどり着くために、よく使うQiitaに列挙しておくことにした Streamや大学専用サイ
-
「線形代数を簡単に理解できるようになりたい…」。そう思ったことはないでしょうか。当ページはまさにそのような人のためのものです。ここでは線形代数の基礎のすべてを、誰でもすぐに、そして直感的に理解できるように、文章だけでなく、以下のような幾何学きかがく的なアニメーションを豊富に使って解説しています。ぜひご覧になってみてください（音は出ませんので安心してご覧ください）。 いかがでしょうか。これから線形代数の基礎概念のすべてを、このようなアニメーションとともに解説していきます。 線形代数の参考書の多くは、難しい数式がたくさん出てきて、見るだけで挫折してしまいそうになります。しかし線形代数は本来とてもシンプルです。だからこそ、これだけ多くの分野で活用されています。そして、このシンプルな線形代数の概念の数々は、アニメーションで視覚的に確認することで、驚くほどすんなりと理解することができます。 実際のと
-
俺はさっきまで知らなかった。これはやばすぎるので増田に書いて広めようと思う。（追記にも書いたが、公式の英語字幕があるので聞き取れなくても心配しないでほしい。） 以下のリンクから飛べる。 https://nptel.ac.in/courses リンク先を見ればすぐ分かると思うが、驚くべきは、カバーしている分野の広さだ。アメリカのMOOC(Udacityだの、Udemyだの)は、表層的な、「すぐ使える技術」の講座ばかりで、オペレーティングシステムやコンピュータネットワーク、あるいは偏微分方程式や代数学といった、コンピュータサイエンスや数学等の基礎学問のような分野はあまりカバーされていない。（主観だが、恐らく正しいはずだ。Udacityのジョージア工科大のコンピュータサイエンスの授業は別だが、数は少ないし、それにしても数学はカバーしていない。） しかし、この「NPTEL」では、自分に関わりのある
-
Search, watch, and cook every single Tasty recipe and video ever - all in one place! News, Politics, Culture, Life, Entertainment, and more. Stories that matter to you. 「このままでは8割減できない」 「8割おじさん」こと西浦博教授が、コロナ拡大阻止でこの数字にこだわる理由緊急事態宣言も出て、新型コロナウイルスの流行拡大を防ぐため人との接触を8割減らすことが求められている。ところが、緊急事態宣言直前に誰かに資料の数値が書き換えられ、「7〜8割削減」「6割でもいいのか」など、様々な数字が出回っている。8割削減という目標をはじき出した「8割おじさん」こと西浦博さんを取材した。
-
私はタイムラインとトレンドを一切見ないタイプのツイ廃なので、流行の話題に乗り遅れることが多々ある。（それでいいと受け入れている） そのため「不登校だった（？）VTuberが積分についてイチから勉強する配信」が少し前に話題になっていたらしいと今さら知った。 私はVTuberのオタクではない。ときどきのらきゃっとさんの放送を観るくらいで、今をときめくホロライブとかにじさんじについては何も知らない。 ただ、私は数学ガールのオタクである。 数学ガールとは、ラノベ風の数学読み物シリーズだ。ラノベと言っても、扱う数学は高校〜大学レベルかそれ以上と、ガチである。（派生した『数学ガールの秘密ノート』シリーズでは中学〜高校レベルの易しい内容を扱っている） 私は本当に数学ガールシリーズが好きで好きでたまらなく、約1年前からはレビュアーとして出版前の原稿を読ませて頂いている。だから「著者からの回し者とかではござ
-
音階の数学｜じーくどらむす
- 1297 users
- note.com/geekdrums
- 学び
- 2020/08/02
私の大好きな数学者の名言で、「音楽は感性の数学であり、数学は理性の音楽である」という言葉があります。 数を原理とするピタゴラス教団がピタゴラス音律を作り出し、そこから純正律という整数比率によるハーモニーを重視した音律が作られたことからも、音楽と数学の関係性は深いと言えるでしょう。 しかし、 実際に数学を多少わかって、音楽を多少嗜んでいる方であれば、音楽で使われる様々な単位への違和感を感じたことがあるのではないでしょうか。 とにかく既存の音楽理論や音楽文化が、「12音種」「7幹音」「5線譜」「1から数える」すべてが噛み合っていない感じがすごい。この噛み合ってない上で究極の覚えゲーを重ねがけして理論作り上げてんのヤバい。 — じーくどらむす/岩本翔 (@geekdrums) July 12, 2020 音楽を取り巻く数への違和感まずこの「12音階」（ド～シまで、＃、♭も含めた1オクターブ以内の
-
積分とは・対数とは・微分とは〜「分かる」とはどういうことか〜
- 1169 users
- togetter.com
- 学び
- 2020/08/06
文系向け「統計学」の授業で、積分・対数・微分を復習する機会があった。その時の「1枚スライド」を公開した。この図をめぐって、「分かる」とはどういうことか、について多くのコメントをいただいた。それを、まとめました。（話が同時並行で進行するので、スレッド風の「まとめ」です。） 注意：積分は、統計学の場合、正規分布表を見るために必要。対数の必要性は、尤度関数（尤もらしさ）の対数をとって計算を簡単にする式変形で使うため。微分の必要性は、確率密度関数の最大値（尤度最大の条件）を求めるため。どれも統計学で必須の内容。 注意２：（追記8/6）ここに出てくる「指数、対数、微分、積分」は「感染症の数理モデル」の基礎となっている。 注意３：（追記8月9日）番外編『「積分」と「源氏物語」〜「晩年の清少納言」から「京都女子大」まで』へのリンクはこちらです。https://togetter.com/li/157284
-
スタンフォード大学の教授で数学者の時枝正（ときえだ・ただし）は、「おもちゃ」を使って数学や物理の定理を解き明かす。スープ皿や木のレール、大きなコインを手に、「ショー」とも呼べそうな講義をいかにも楽しげに始めるその姿に、聴衆は一瞬にして心を惹きつけられるという。 数学者には二つのタイプがいるという──。一つは、チョークを握り黒板に向かう、理論派タイプ。もう一つは、フェルトペンとホワイトボードを使う、どちらかというと応用数学系の人である。 その伝でいうと、時枝正は第三のタイプの数学者である。しかもこの第三のタイプは、世界広しといえども彼一人だけの可能性がある。 時枝は仕事道具をどれも煎餅の空箱から取り出すのだが、箱は「すべて同じブランドのもの」なのだそうだ。たとえばその中身は、見かけはそっくりなのに、転がるものと転がらないものがある二つの不思議な構造物。ひもや輪ゴム、クリップの扱い方は、まるで
-
セガは6月15日、社内勉強会で使った線形代数の教材を、公式ブログで無償公開した。ページ数は150以上。ゲーム開発に必要な3DCGの技術的基礎となる知識を学び直すために使ったものという。 2020年に行った社内勉強会向け教材の一部をPDF形式で公開。全8部構成で、ベクトルや行列、3次元での回転を計算するときに使う「クォータニオン」について教える。ただし簡潔に分かりやすく学べるよう編集したため、用語の定義が一般的なものと異なる場合があるとしている。 ゲーム制作では、キャラや背景を3次元で回転させたり、ゲームエンジンそのものを作ったりするときに線形代数を使うという。セガは教材について「興味のある方は参考にしてほしい。“大人の学び直し”をしてみたい方はぜひ」としている。 関連記事 任天堂がSwitch向けにプログラミング学習ソフト 作ったゲームの共有機能も 任天堂が、Nintendo Switch
-
サインインした状態で「いいね」を押すと、マイページの 「いいね履歴」に一覧として保存されていくので、 再度読みたくなった時や、あとでじっくり読みたいときに便利です。
-
なぜ、微積分は役に立つのか
- 1044 users
- wirelesswire.jp
- 学び
- 2023/11/29
なぜ、微積分は役に立つのか 2023.11.27 Updated by Atsushi SHIBATA on November 27, 2023, 14:58 pm JST 今回紹介する書籍：『はじめての物理数学』永野 裕之（SBクリエイティブ、2017） 朝起きてから寝るまで、我々は何種類もの「数」を見ます。 私自身、朝起きるとネットやニュースで降水確率、予想気温のように気象にかかわる数、為替、海外の株式市場の指数など、いろいろな種類の数をチェックします。しばらく前なら、コロナウイルスの感染者数や増加傾向を表す指数を毎日のように確認していました。 自分を取り巻く環境を知るために、私たちはいろいろな「数」を確認します。そして数を手がかりにして、行動を決めます。現代を生きる私たちにとって「数」は、世界を知るための「目」としての役割を持っています。 現代人が日常的に見るこの種の数は、たいてい計
-
1. はじめに こんにちは、東京大学 3 年の米田と申します。この度は、ダイヤモンド社から『高校数学の基礎が 150 分でわかる本』という書籍を出版させていただくことになりました。高校数学の基礎を図解で超わかりやすく説明した本です。 【フルカラー図解】高校数学の基礎が 150 分でわかる本 - Amazon 発売日は 3 週間後の 2023/7/26 です。電子書籍版も同時期に出る予定です。本記事では、この本の内容や特徴について、簡単に紹介させていただきます。 2. この本はどういう本か 本書は、主に次のような方に向けた、高校数学の「超」入門書です。 高校数学をはじめて学ぶ方 数学を学び直したい方 日本ではたくさんの数学の本が毎週のように出版されています。しかしこの中の多くは、難しくて多数の人が挫折してしまうか、雰囲気でわかった気にはなるけど結局身に付かないかのいずれかです。 そこで本書は
-
文系パパエンジニアが放送大学等でコンピュータサイエンス・数学を学んで理系学士を取りに行く話 - とあるCS学徒のブログ
- 1036 users
- wbspry.hatenablog.com
- テクノロジー
- 2021/02/24
※取りに行く話なのでまだ取ってません。 界隈ではコンピュータサイエンス（以下CS）を学ぶことが流行っていますが、これはとあるパパのとある一例です。どなたかの参考になれば。 こちらの通り申請致しました。 https://t.co/IDkVJAWjc2— Y (@wbspry) 2021年2月13日 誰？ 事の経緯 なぜ大学でCS・数学を学びたいのか CS系学位を課す外資大企業たち CSできるマンへの憧れ 立ちはだかる数学の壁 dynamicなものよりstaticなもの ところで、CSって何？ 選択肢と選択 なぜUoPeopleではなかったか 週次の人巻き込み課題が大変そう 単位移行が可能なのか（※当時は）よくわからなかった とはいえ なぜ帝京理工通信ではなかったか なぜJAISTではなかったか 学位授与機構との出会い 新しい学士への途（単位累積加算制度）とは 学位取得までの流れ そして単位集
-
楽天よりPCR検査キットが販売開始となりました。 このキットを用いることで、病院を受診することなくPCR検査が施行可能とのことです。 しかし、PCR検査は医療従事者によって正しい方法で検体を採取し、正しく結果を解釈せねばなりません。 筆者は感染症専門医ですが、一般の方がこのPCR検査キットを使用することは推奨しません。 楽天から販売されているPCR検査キットとは4月20日より楽天でPCR検査キットが販売開始になっています。 新型コロナウイルスPCR検査キット COVID-19 PCR 「本検査キットは、ジェネシスヘルスケア株式会社が開発し、楽天株式会社が法人窓口となりサービスを提供しています。」とのことです。 4月21日21時時点でホームページには「現在、大変多くのお申込みをいただいており、順次ご対応をさせていただいております。ご回答にお時間がかかる場合がございますが、何卒ご容赦いただきま
-
---【追記：2022-04-01】--- 「基礎線形代数講座」のPDFファイルをこの記事から直接閲覧、ダウンロードできるようにしました。記事内後半の「公開先」に追記してあります。 --- 【追記ここまで】--- みなさん、はじめまして。技術本部 開発技術部のYです。 ひさびさの技術ブログ記事ですが、タイトルからお察しの通り、今回は数学のお話です。 ＃数学かよ って思った方、ごめんなさい（苦笑） 数学の勉強会 弊社では昨年、有志による隔週での数学の勉強会を行いました。ご多分に漏れず、コロナ禍の影響で会議室に集合しての勉強会は中断、再開の目処も立たず諸々の事情により残念ながら中止となり、用意した資料の配布および各自の自学ということになりました。 勉強会の内容は、高校数学の超駆け足での復習から始めて、主に大学初年度で学ぶ線形代数の基礎の学び直し 、および応用としての３次元回転の表現の基礎の理解
-
Skip to the content. 機械学習の研究者を目指す人へ 機械学習の研究を行うためには、プログラミングや数学などの前提知識から、サーベイの方法や資料・論文の作成方法まで、幅広い知識が必要になります。本レポジトリは、学生や新社会人を対象に、機械学習の研究を行うにあたって必要になる知識や、それらを学ぶための書籍やWebサイトをまとめたものです。 目次 プログラミングの準備 Pythonを勉強しよう 分かりやすいコードを書けるようになろう 数学の準備 最適化数学を学ぼう 基本的なアルゴリズムとその実践 機械学習の全体像を学ぼう 基本的なアルゴリズムを学ぼう 深層学習の基礎を学ぼう scikit-learnやPyTorchのチュートリアルをやってみよう サーベイの方法 国際会議論文を読もう Google Scholarを活用しよう arXivをチェックしよう スライドの作り方 論文の
-
分野が広く、さまざまな知識を求められる数学や物理学。これらの知識をツリー構造により分からないところまでひたすら掘り下げて、基礎の基礎から学ぶことができる学習サイトが「コグニカル」です。一体何かどう学べるのか？ということで、実際にコグニカルを使ってみました。 コグニカル https://cognicull.com/ja コグニカルのトップページはこんな感じ。「ばねの弾性力による位置エネルギー」「位置エネルギー」など、数学・自然科学・工学のさまざまな知識が353個並んでいます。 試しに「熱振動」をクリックすると、「熱振動とは、分子など、原子の集合で生じる原子の振動のことです。」と、熱振動について記述されたページが表示されました。また、分子と原子が振動している様子のイメージがアニメーションで表示されています。 読み進めていくと、「説明が理解できない場合」は「以下の知識が不足している可能性がありま
-
未解明だった数学の超難問「ABC予想」を証明したとする望月新一・京都大数理解析研究所教授（51）の論文が、同所が編集する数学専門誌に掲載されることが決まった。3日、京大が発表した。ABC予想は、素因数分解と足し算・かけ算との関係性を示す命題のこと。4編計646ページからなる論文は、斬新さと難解さから査読（論文の内容チェック）に8年かかったが、その正しさが認められることになった。有名な数学の難問「フェルマーの最終定理」（1995年解決）や「ポアンカレ予想」（2006年解決）の証明などと並ぶ快挙となる。【阿部周一、松本光樹】 望月教授は2012年8月、構想から10年以上かけた「宇宙際タイヒミューラー（IUT）理論」の論文4編を、インターネット上で公開した。これを用いればABC予想など複数の難問が証明できると主張し、大きな注目を集めたが、既存の数学が存立する枠組み（宇宙）を複数考えるという構想は
-
Study-AI株式会社は3月23日から、特設サイトとYouTube公式アカウントにおいて、中学生でも人工知能（AI）の勉強を目指せるとうたう「中学生から分かるAI数学講座」動画の無料配信を開始した。 本講座は、一般社団法人日本ディープラーニング協会（JDLA）が提供する「E資格」で出題される数式を読めるようになることを目的としており、中学校や高校の数学を予習（復習）するといった内容だ。 解説範囲は数式の読み方や計算方法で、数式の意味は解説に含まない。到達目標はΣやexpやlogなどの言葉が出てきても抵抗なく受け入れ、計算ができること。対象者はAIの勉強を進めたい人、高校数学を習っていない中学生。 制作意図としては、自分で勉強を進めたり講義を聞いたりするときに「教科書に出てくる数式が読めない」「見たこともない」ということがないように準備体操、予習の一助として作成したとしている。 気になる人
-
2021年、企業が無償公開した新人エンジニア向け研修資料 機械学習やゲーム開発、AWS入門、数学などさまざま
- 936 users
- www.itmedia.co.jp
- テクノロジー
- 2021/12/24
2021年、企業が無償公開した新人エンジニア向け研修資料 機械学習やゲーム開発、AWS入門、数学などさまざま（1/2 ページ） 2021年、さまざまな企業が自社の社内研修資料を無償公開したことが話題になった。ITmedia NEWSでは主に、新人エンジニア向けに公開した資料などを記事として取り上げたところ、多くの反響が集まった。 学べる内容は、機械学習やIT業界の文化、ゲーム開発、セキュリティ、AWS入門、数学など各社さまざま。100ページ以上のスライドや5時間を超える動画などの資料もあり、新人教育への力の入れ具合も垣間見える。改めて、2021年に企業が無償公開した、社内研修資料を取り上げた記事を紹介する。 セガ、3DCG技術の基礎に役立つ数学資料 セガは6月15日に、2020年に社内勉強会で使った線形代数の教材を公式ブログで公開した。ゲーム制作では、キャラクターや背景を3次元で回転させた
-
基礎線形代数講座
- 934 users
- www.slideshare.net/slideshow
- テクノロジー
- 2021/06/15
4. 公開にあたって ●まえがきに代えて 本書は 株式会社 セガ にて行われた有志による勉強会用に用意された資料を一般に公開するもので す。勉強会の趣旨は いわゆる「大人の学び直し」であり、本書の場合は高校数学の超駆け足での復習 から始めて主に大学初年度で学ぶ線形代数の基礎の学び直し、および応用としての３次元回転の表現の 基礎の理解が目的となっています。広く知られていますように線形代数は微積分と並び理工系諸分野の 基礎となっており、だからこそ大学初年度において学ぶわけですが、大変残念なことに高校数学では微 積分と異なりベクトルや行列はどんどん隅に追いやられているのが実情です。 線形代数とは何かをひとことで言えば「線形（比例関係）な性質をもつ対象を代数の力で読み解く」 という体系であり、その最大の特徴は原理的に「解ける」ということにあります。現実の世界で起きて いる現象を表す方程式が線形な振
-
2013年の秋、その時の自分は30代前半だった。 衝動的に数学を学び直すことにした。 若くないし、数学を学びなおすには遅すぎると思って尻ごみしていたが、そこを一念発起。 というか軽い気持ちで。ぶっちゃけると分散分析とやらに興味を持ったから。 数学というか統計かな。 統計的に有意差があったといわれてもその意味がさっぱりだった。 一応、理系の大学を出てるので、有意差という単語をちょいちょい耳にはしていたが、 「よくわかんないけどt検定とかいうやつやっとけばいいんでしょ？」 くらいの理解だった。 で、ありがちな多重比較の例で、3群以上の比較にt検定は使っちゃダメだよっていう話を聞いて、なんか自分だけ置いてけぼりが悔しくなって、Amazonをポチッとしたのが全ての始まり。 あと、あの頃はライン作業の工員だったから、脳が疲れてなかったし。 そんなわけで、自分の軌跡を晒してみる。 みんな数学とかプログ
-
私は数学がなぜ苦手なのか？高校生が分析してあみ出した勉強法が効果抜群だった｜高校生新聞オンライン｜高校生活と進路選択を応援するお役立ちメディア
- 924 users
- www.koukouseishinbun.jp
- 学び
- 2022/05/31
私は高校入試で、数学以外の科目は 80～90点台でしたが、数学だけ55点でした……（合格者平均は約70点）。しかし試行錯誤の結果、定期テストで平均より少し上となり、評定平均4、模試偏差値65くらいを取れるようになりました。その方法について紹介します。（高校生記者・みかみ＝３月卒業） なぜ苦手か分析してみたら 数学が苦手だった原因を分析してみました。「解けない問題の解答を丸暗記しようとしていたこと」「解答用紙やノートがうまく使えないこと」「暗記するなという言葉を曲解し、復習せず思考停止していたこと」とわかりました。そこで、主に次の4つの方法を実践してみました。 【１】自分の言葉に変えてみる まず、私には数学特有の言い回しが難しかったので、問われた内容を自分の言葉に変えて、問題集に解答の流れを書き込みました。そしてセルフレクチャーという方法で、問題を見て瞬時に答えが導き出せるようにしました。
-
【Python】専門書や論文を読みたいけど数学が苦手・わからない人向けのコードを読んで学ぶ数学教本 - Qiita
- 921 users
- qiita.com/PHVTuber
- テクノロジー
- 2021/10/24
はじめに プログラミング自体は文系、理系、年齢関わらず勉強すればある程度ものになります。プログラミングがある程度できるようになるとTensorflow,PyTorchやscikit-learn等のライブラリで簡単にできる機械学習やデータサイエンスに興味を持つの必然! これからさらになぜ上手くいくのか・いかないのかの議論をしたい、社内・外に発表したい、理論的な所を理解したい、先端研究を取り入れたい、応用したい等々と次々に実現したい事が増えるのもまた必然でしょう。このときに初めて数学的なバックグラウンドの有無という大きな壁が立ちはだかります。しかし、数学は手段であって目的ではないので自習に使える時間をあまり割きたくないですよね。また、そもそも何から手を付けたら良いかわからないって人もいるかと思います。そんな人に向けた記事です。本記事の目標は式の意図する事はわからんが、仕組みはわかるという状態に
-
旧限界数学ゼミガール
- 913 users
- semigirls.conohawing.com
- 学び
- 2020/10/08
某所に投稿していた限界数学ゼミガールのまとめです(2019.11.27 ~ 2019.12.22) 公理的集合論と数理論理学がメインです。 第一話 「巨大基数の崩壊」 第二話 「クレパの木」 第三話 「ペアノの公理系」 第四話 「ストーンの表現定理」 第五話 「ゲーデルの不完全性定理」 おまけ 最初期の落書きです この頃から寝ている子が頭が良いキャラ（議論が詰まった時のブロックバスター）というのはぼんやりながら固まってました（笑）
-
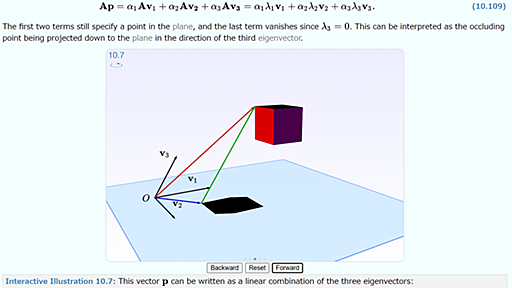
「Immersive Math」は、数学のうちベクトルや行列などの計算を研究する分野である「線形代数」についてインタラクティブな図を用意することでわかりやすさを向上させた無料の教科書サイトです。 Immersive Math https://immersivemath.com/ila/index.html サイトのトップページはこんな感じ。「完全にインタラクティブな図を備えた世界で最初の線形代数本」と述べられています。 中央に表示されている三角形の図はインタラクティブで、左上をクリックすることで回転・停止を切り替えられるほか、各頂点をクリックしてドラッグ＆ドロップすることで位置を調整可能。自由に図を編集できるため理解しやすいというわけです。 ページをスクロールすると目次が現れました。まずは「Preface(序文)」をクリック。 「『百聞は一見に如かず』という言葉の通り、たくさんの言葉を重ね
-
ステレオタイプに負けじと頑張る人は立派だ。 しかし意識することが、逆にステレオタイプ的結果を生じさせることがある。 試験を実施するには、この問題を考えなくてはいけない。 2020/12/01 追記 本記事は『ステレオタイプの科学』という本を参考に書いたが、最近の研究では再現性があまり無いとのこと。それを念頭において読んでもらいたい。 この邦訳の原書は、10年以上前（心理学の再現性の危機が議論される前）に出たもので、最近の研究では、元になった実験の再現性はあまりないと言われています。https://t.co/RKmwQXfLZm— 'Yuki’ Kamitani (@ykamit) August 28, 2020 "Stereotype threat" is such a weak research program with findings that don't replicate in
-
ラマヌジャンは本当に何も知らなかったのか
- 846 users
- mathlog.info
- 学び
- 2023/11/13
$$\newcommand{a}[0]{\alpha} \newcommand{Aut}[0]{\operatorname{Aut}} \newcommand{b}[0]{\beta} \newcommand{C}[0]{\mathbb{C}} \newcommand{d}[0]{\delta} \newcommand{dis}[0]{\displaystyle} \newcommand{e}[0]{\varepsilon} \newcommand{F}[4]{{}_2F_1\left(\begin{matrix}#1,#2\\#3\end{matrix};#4\right)} \newcommand{farc}[2]{\frac{#1}{#2}} \newcommand{G}[0]{\Gamma} \newcommand{g}[0]{\gamma} \newcommand{Gal}[0]
-
「その数自体は0でないのに、2乗するとはじめて0になる数」ってなんですか？ そんな数あるはずがないと思いますか？ でももしそんな数を考えることができるなら、ちょっとワクワクすると思いませんか？ 今回はそんな謎の数のお話。 実数の中には、「2乗して0になる数」というのは0しかありません。 （2乗して0になる実数は0しかない図） ということは、「2乗してはじめて0になる数」というのがあるとしたら、それは実数ではありえません。 「1年A組にはメガネの人はいないので、メガネの人がいたとしたらその人は1年A組ではありえない」くらいの当たり前のことを言っています。 この辺の議論は、複素数で「」を導入したときと同じですね。 「実数の中には、2乗して-1になる数というのは存在しないので、それがあるとしたら実数ではありえない」ということで「虚数」であるが導入されるわけです。 それならばということで、ここでは
-
計算量についてのお話です。対象は、プログラミング経験はあるが計算量のことを知らない初心者から、計算量のことを知っているつもりになっている中級者くらいです。 数式を見たくない人にとっては読むのが大変かもですが、深呼吸しつつ落ちついて読んでくれるとうれしいです。 それから、この記事が自分には合わないな〜と思ったときは、（別の記事を Qiita とかで検索するよりも）この記事の一番下の 参考文献 にある本を読むことをおすすめします。Amazon の試し読みで無料で読めます*1。 TL; DR 関数の増加度合いのことをオーダーと呼ぶよ 計算量は、入力サイズ（など）を受け取ってアルゴリズムの計算回数（など）を返す関数だよ その関数のオーダーについての議論がよく行われるよ オーダーを上から抑えるときは \(O\)、下から抑えるときは \(\Omega\) を使うよ オーダーを上下両方から抑えたいときは
-
数学市民@Mathpedia運営 @Infinity_topoi 高3の受験生を見ていた時、計算力の低さを見かねて中1の計算問題集を解かせたことがあった。「これくらい出来るよ」って最初は笑っていたが、制限時間をつけてやるとボロボロだった。流石にショックを受けていたが、「これくらいは出来る」と思って基礎的な事をやり直せないのはよくあることだと思う。 数学市民@Mathpedia運営 @Infinity_topoi それからひたすら数か月基礎計算。満点以外は全部やり直しで徹底的にやった(何度も泣かせてしまった)。そのあともう一度高校数学をやってみたら、すんなり出来るようになって、しまいには「センター数学って簡単じゃないすか？」とか言い出した(無事現役合格した)。計算力って本当に大事と思った一例。 数学市民@Mathpedia運営 @Infinity_topoi この生徒の場合でもそうだけど、計
-
「映像も物理も、微分可能になるとすごいことが起きる」ということの意味を文系にもわかるように説明しようと試みる 2021.07.26 Updated by Ryo Shimizu on July 26, 2021, 07:12 am JST 最近のプログラミングの新しい波は微分可能プログラミング(differentiable programming)である。 微分可能プログラミングとは、簡単に言うと・・・と思ったが、簡単に言うのは結構難しい。 まず「微分」という言葉があまり簡単ではない印象がある。 まずは微分と積分の関係性を説明しておこう。文系の読者に向けた記事であるので、非常にざっくりと説明してみよう(そのかわり、元々数学が得意な読者にとっては直感的ではない説明になるかもしれない)。 まず、瓶からコップにジュースを移すような状況を想定してみる。 瓶からコップが一杯になるまで60秒で注ぐとし
-
こういう人間です ・ 文系（英文学科） ・ Webエンジニア ・ 統計を勉強中モチベーションここ２年ほど統計を勉強しているのですが、そこで毎回立ちふさがるのが数学の壁でした。わたしは文系ということもあって数ⅡB（しかも途中まで）しか履修していなかったため、微分積分や線形代数などが出てくると理解することが難しく時間がかかってしまいます。 でももっと統計を知りたいし理解したい 😭 という気持ちをずっと感じていて今回数学をやり直すことにしました。 高校３年分と考えるとなかなか決心するのに時間がかかりましたが、やってよかったと思います。スケジュール感や実際使った本などを共有することで同じような方の参考になればよいなあ、と思います。 実際使用した本 ・ 講座■ よくわかる数学シリーズ 主にMY BESTシリーズを使用しました。カラーで説明もわかりやすく、目にも心にもやさしい仕上がりになっております
-
人は知ってることしか見えない - いつか博士になる人へ
- 760 users
- www.ki1tos.com
- 学び
- 2020/06/23
大学院に入ったばかりの頃、配属された研究室で研修を受けた。 僕は先輩について回って、実験機器を使ってみたり、実験ノートのとり方を教えてもらったりした。 ある日、先輩が先生たちとミーティングをするというので見学させてもらった。 そのときのことは今でもよく覚えている。 最初に、先輩が実験でとれたデータについて説明した。 先輩の堂々とした説明を聞いて、僕はとても感銘を受けた。 ふんふんとうなずきながら、はたして自分はこんなふうに説明できるだろうか（いや、できない）と思っていた。 でも先輩の説明が終わったとき、 「なんか変だね」 と助教さんが言った。そして、 「普通はこうなるはずなんだけど」 と、他のデータとの違いを指摘した。 先輩と僕は他のデータを知らなかったから、そこが変だと気がつかなかった。 なぜこのデータは変なんだろうねと、皆でうんうん考えていると、 「３次元でグラフを描いてみて」 と先生
Mathematicsの関連エントリー
新着記事
キーボードショートカット一覧
j次のブックマーク
k前のブックマーク
lあとで読む
eコメント一覧を開く
oページを開く
Copyright © 2005-2024 Hatena. All Rights Reserved.
設定を変更しました