三角関数は人類の叡智であり、私達の生活の基盤を支えているものです。 しかし特定の職業に就く方々に必要とされる専門知識の範疇ではないでしょうか? 全国津々浦々の高校生に教える知識としては、三角関数よりも金融経済の基礎の方が優先度が高… https://t.co/QBSj96rb9k
絞り込み
-
検索対象
-
ブックマーク数
-
期間
-
セーフサーチ
mathの検索結果361 - 400 件 / 2879件
-
論文の探し方 / 読み方 - Qiita
- 334 users
- qiita.com/lychee1223
- テクノロジー
- 2024/12/23
Deleted articles cannot be recovered. Draft of this article would be also deleted. Are you sure you want to delete this article? 本記事は K3 Advent Calendar 2024 23日目の記事です 本記事では、趣味がSurveyで毎日論文漬けの僕から、論文の探し方・読み方のTipsを伝授します! もちろん、研究分野によっても論文の書き方や特徴は変わってきます!基本的に普遍的なことを書くつもりですが、僕の専門であるコンピュータサイエンス・機械学習・コンピュータビジョン・自然言語処理の分野に依存した部分もたたあると思います!あくまで参考程度に、もし指導教員の話とコンフリクトしたら、そちら優先してマージしてください! この記事を読んでる人の中には、来年度から研
-
コンピュータシステムの理論と実装 第2版
- 334 users
- www.oreilly.co.jp
- テクノロジー
- 2024/11/05
コンピュータシステムをゼロから作って学ぶベストセラー書の改訂第2版。コンピュータを理解するための最善の方法はゼロからコンピュータを作ることです。コンピュータの構成要素は、ハードウェア、ソフトウェア、コンパイラ、OSに大別できます。本書では、これらコンピュータの構成要素をひとつずつ組み立てます。具体的には、NANDという電子素子からスタートし、論理ゲート、加算器、CPUを設計します。そして、アセンブラ、仮想マシン、コンパイラ、OSなどを実装しコンピュータを完成させて、最後にその上でアプリケーション(テトリスなど)を動作させます。 賞賛の声 訳者まえがき まえがき 第I部 ハードウェア I.1 Hello, World Below(こんにちは、低レイヤの世界) I.2 Nand to Tetris I.3 抽象化と実装 I.4 方法論 I.5 この先の展望 1章 ブール論理 1.1 ブール代数
-
「僕たちに証明できないですかね」数学好き高校生が常識破りの成果、海外誌に掲載|高校生新聞オンライン|高校生活と進路選択を応援するお役立ちメディア
- 333 users
- www.koukouseishinbun.jp
- 学び
- 2023/10/05
「大学で学ぶ知識がないと解けない」とされていた数学の証明問題。西宮市立西宮高校(兵庫)の3年生4人は約1年かけて、高校で学ぶ知識のみで証明してみせ、オーストラリアの数学専門誌に論文が掲載された。常識を覆した4人の熱意に迫る。(文・黒澤真紀、写真・学校提供) もともとは週に1度、「総合的な探究の時間」(現高2以降は「理数探究」)の授業で4人は円周率の新しい求め方を探していたが、うまくいかなかった。試行錯誤する中で「円に内接する多角形の中で、正多角形が一番大きな面積を持つということをなぜ言えるのか」と新たな疑問が浮かんだ。 非常勤講師の宮寺良平先生に質問すると「証明するには、大学の数学科1年生以上のレベルの知識が必要」と言われた。 「僕たちに証明できないですかね」。生徒たちは諦めなかった。「内容自体はシンプル。高校で習う範囲でも太刀打ちできるのではないか」という田中陸人さんの言葉に全員が同意。
-
僕は経済学研究科に所属する大学院生です。 ただし経済学の中でも特殊な領域を専攻しており、「どんな社会が”良い"社会か?」「”公平な"資源の配分とは何か?」など哲学的な問いを扱っています。 この記事では、初歩的な数学以外は前提知識なしに、社会的選択理論(経済学の一分野。社会についての哲学的な問いに対して数学でアプローチする)のイメージを共有してみたいと思います。具体的にはより細かいテーマとして最近取り組んでいるPopulation Ethicss(人口倫理)について取り上げます。 Population Ethicのモチベーションを紹介しながら、Ng(1989)によって示された不可能性定理を証明も含めて説明します。 「数学をこんな問題を考えるのに使っているんだ!」「経済学の中にはこういう領域もあるんだ」みたいなことを共有できたら嬉しいです。 長い旅にはなりますが、ぜひ経済学の中でも特殊な世界を
-
新型コロナウイルスによる日本の死者数は欧米に比べて少ない。だが感染者数と死亡者数を「対数グラフ」で分析すると、日本だけが異常な推移をたどっている。統計データ分析家の本川裕氏は、「他国のように収束へ向かう横ばい化への転換が認められず、増加ペースが落ちていない。そこには3つの理由が考えられる」という——。 世界中で日本だけ「コロナ感染のグラフがおかしい」 新型コロナウイルスは、海外でも日本でも「感染爆発」と呼ばれた一時期ほどの急拡大は見られなくなってきた。だが、それでもなお深刻な感染状況が続き、医療が対応しきれないこともあって各国で死者が増えている。 1月に中国・武漢ではじまった新型コロナの感染拡大は、その後、韓国、イラン、イタリアなどと広がり、また、さらに欧州各国や米国などを中心に全世界に拡大してきている。この4カ月余りを過ぎた時点で、地域によって感染拡大のテンポや規模がどのように違っている
-
ITスキルロードマップ roadmap.sh がすごい。AI and Data Scientist について対応する本をまとめた - Qiita
- 331 users
- qiita.com/aokikenichi
- テクノロジー
- 2024/04/09
ITスキルロードマップ roadmap.sh がすごい。AI and Data Scientist について対応する本をまとめた機械学習データ分析キャリアデータサイエンスデータサイエンティスト Developer Roadmapsというサイトがすごいです。ITエンジニアの分野別にスキルアップのロードマップが示されています。 言語、基盤、アプリ、かなり網羅されています。 その中のAI and Data Scientist Roadmapについての推薦図書まとめです。 雑感 これだけ学んでいれば「こいつ知ってるな」感がありますね。ただ気になる点としては ビジネス、ドメイン知識や分析目的定義などのスキルについて言及がないのは残念。 いきなり数学から入るコースになってますが、一旦は飛ばしてコード写経してから戻ってきても良いと思います。ここで挫折すると勿体無いので。 計量経済学重視の観点はいいですね
-
新型コロナウイルスの感染に関わる、せきなどの飛まつがどう広がるのか、最新のスーパーコンピューターで予測した動画を、神戸市の理化学研究所が公開しました。 この動画は、理化学研究所の坪倉誠チームリーダーなどのグループが、研究の中間報告として報道各社に公開しました。 予測には最新のスーパーコンピューター「富岳」が使われていて、机をはさんで人が対面しているケースでは、1人がマスクをせずにせきをした場合、口元を隠すくらいの高さの仕切りを間に置いていても、向かいにいる人の顔に飛まつがかかっています。 一方、頭の高さより高い仕切りであれば、飛まつをせき止めています。 また、時速80キロの電車が窓を開けて走行した場合でも、通勤ラッシュ時のような満員の状態だと、空気の流れが止まり、十分な換気ができないこともわかったということです。 坪倉チームリーダーは「『富岳』の計算能力によって、飛まつや空気の流れを細かく
-
はじめに マケデコというMarket APIを活用した投資を話しあうコミュニティでExcelを用いてファンダメンタル分析のために日本株全銘柄を無料でデータ取得する方法をマケデコがSBIネオトレード証券のスポンサーで開発し、セミナーで発表しました。 ダウンロード、使い方など細かい情報は上のページを参照してください。J-Quants APIのアカウント(無料からあります)を必要としますので、そこだけ注意が必要です。ネオトレAPI for Excelとも連携します。 使い方のセミナー動画はこちらですが、長いので今後10分程度にまとめようとおもいます。 各種機能のちら見せ 銘柄リストをダウンロードするとこんな感じ 主要な指数は全部自動で計算されて全銘柄の比較可能な主要なフファンダメンタルが並びます こんな感じで分布の分位を確認しながらスクリーニングができます(Excel 2019では動かないようで
-
歴史が苦手だったのは、こんな昔のイベントや用語を覚えて、いったい何になるんだ?と思ったからだった。 そして、個々の知識が細かすぎて、解くべき問題に結びつくまでが遥か遠い、とでも言うべき感覚が嫌だった。 知識をいくつも覚えて、それらを組み合わせてようやくたった一つの答えがわかる。 しかも、それも知ってるか否かだけ。私個人による創意工夫の余地も無い。端的に面白くない。 それらをもどかしく思っていたのだ。 まとめると、歴史は、覚えることのコスパが悪い知識であり、私個人を疎外する教科だと感じていた。 その点で、数学の知識、つまり、公式は一般性を持つので適用範囲が広いし、私の創意工夫も生かせる。 だから、数学は大好きだった。 公式はひとつ覚えれば、多くの問題に適用できるのだ。覚える個数としても、そんなに多くない。 だから、ビジネス書に書かれた格言が多くの応用と工夫の余地を期待されるように、 私も適用
-
論理的思考力っていったい、何のこと?
- 330 users
- blog.tinect.jp
- 学び
- 2024/11/13
論理的思考という言葉がある。 この言葉は、ビジネスでは大変な人気で、 「論理的思考力を鍛えよ」とか 「論理的思考力を身につけましょう」とか 「ビジネスパーソンに必須の素養」とか そんな言われ方をしている。 ところが、この「論理的思考」という言葉は、実は、最も説明の難しいことばの一つだ。 * もう10年以上前のことだが、コンサルティング会社に在籍していたとき、 「ロジカルシンキング」の研修テキストを作っていたことがある。 ロジカルシンキングとは、日本語では「論理的思考」と訳されるが、私が在籍していたコンサルティング会社では 「難解な用語は、中学生でもわかるくらいにかみ砕いて説明しなさい」 という方針があった。 そのため「論理的」という言葉の正確な定義について調べたのだった。 まずは当然、辞書を引いてみる。 すると、「論理の法則にかなっているさま」とあった。 そこで再度、「論理」について調べた
-
奇数と偶数の区別がつかない人 - Yakinik
- 329 users
- scrapbox.io/yakinik
- 学び
- 2021/01/25
-
宝くじの話なんだけど、「この売り場から高額当選が出ました」って売り場に書かれてることがあるじゃん? あれってよく考えたら、一度高額当選が出たら次は出にくいってことにならないか? 確率論で考えたら同じ売り場で何度も高額当選が出ないよな?当たりは偏らないはずだから。 だから逆に、高額当選が出てない売り場で買うべきでは? まあ売れてる枚数にもよるんだろうけどさ。 【追記】 例えばさ、宝くじが100枚あって1枚だけ当たりだとする。 それを宝くじ売り場AとBに50枚ずつ配る。 過去10回行って、Aでは7回、Bでは3回当たりが出たとする。 すると次の回は、売り場Bで当たりが出そうじゃない?違うの? 【さらに追記】 「ギャンブラーの誤謬」という言葉を知りました。 まだ理解はできてないけど、なんとなく分かった気がします。ありがとうございます
-
暗号研究者。既存暗号の安全性解析や共通鍵暗号の利用モード開発などに携わる。2018年に国際標準にもなっていた認証暗号技術の一つである「OCB2」について、暗号が提案されてから14年間気づかれていなかった安全性の欠陥があることを発見した。暗号研究を始めたきっかけは、興味のあった代数学を使い実社会に応用できる分野だったから。(撮影:日経クロステック) 数多くのデバイスがインターネットにつながるIoT(インターネット・オブ・シングズ)時代に、必要不可欠な技術がある。暗号技術だ。パソコンやスマートフォン、クレジットカード決済端末、生産設備に取り付けられたセンサーをはじめ、さまざまな端末の通信で暗号技術が使われている。暗号技術のおかげで、第三者に見られたり意図しない内容に改ざんされたりせずに、データを安全にやりとりできる。 暗号技術を支える研究者の一人が、NEC セキュアシステム研究所の井上明子だ。
-
「全数調査なら何でもわかる」という誤解 - 間違えがちな母集団とサンプリングそしてベイズ統計 - - ill-identified diary
- 326 users
- ill-identified.hatenablog.com
- 世の中
- 2020/10/21
この文章は pandoc-hateblo で tex ファイルから変換しています. PDF 版はこちら 2021/10/15 追記: 後半のベイジアンブートストラップに関する解説はこちらのほうがおそらく正確です ill-identified.hatenablog.com 概要挑発的なタイトルに見えるかも知れないが, 私はしらふだしこれから始めるのは真面目な話だ — 正直に言えばSEOとか気にしてもっと挑発的なタイトルにしようかなどと迷ったりはしたが. 「全数調査できれば標本抽出の誤差はなくなるのだから, 仮説検定は不要だ」という主張を見かけた. いろいろと調べた結果, この問題を厳密に説明しようとすると最近の教科書には載ってない話題や視点が必要なことが分かった. ネット上でも勘違いしている or よく分かってなさそうな人をこれまで何度か見かけたので, これを機に当初の質問の回答のみならず関
-
","naka5":"<!-- BFF501 PC記事下(中⑤企画)パーツ=1541 -->","naka6":"<!-- BFF486 PC記事下(中⑥デジ編)パーツ=8826 --><!-- /news/esi/ichikiji/c6/default.htm -->","naka6Sp":"<!-- BFF3053 SP記事下(中⑥デジ編)パーツ=8826 -->","adcreative72":"<!-- BFF920 広告枠)ADCREATIVE-72 こんな特集も -->\n<!-- Ad BGN -->\n<!-- dfptag PC誘導枠5行 ★ここから -->\n<div class=\"p_infeed_list_wrapper\" id=\"p_infeed_list1\">\n <div class=\"p_infeed_list\">\n <div class=\"
-
この技術が分からん2020 - laiso
- 325 users
- laiso.hatenablog.com
- テクノロジー
- 2020/12/19
2020年に作ったソフトウェアや開発技術をふりかえる で分かったことばかり書いたけど相変わらずなんべん勉強しても分からんな〜と思うことも多いのでそれもリストアップしてみることにした。 SQL 10年以上触っているはずだけど集合のイメージが頭に入ってこなくて全然文を組み立てられずにいる。ゆるふわORMを適当に使ってる。 CSS 10年以上触っているはずだけど制約のイメージが頭に入ってこなくて全然レイアウトを組み立てられずにいる。ゆるふわTailwindCSSを適当に使ってる。 Unity 何回もダウンロードして教材を買ってるんだけど。アセットを組み立てて何か意味のあるものを作るっている状態まで行かない。Flashは使いこなしていたはずなのになぜ UIデザイン 作る時に一定の理屈っぽいこだわりがあるんだけど、何か自分で作るというところまでいかない上に、深く理由を考えたことすらなかったので、こだ
-
神山 翼@お茶大・気象学 @kohyama_met こうやま・つばさ。お茶の水女子大学理学部・理学専攻の教員(情報科学)。主要業績: 月と降水(Kohyama and Wallace 2016, GRL)、ラニーニャ的温暖化(Kohyama et al. 2017, J Clim)、黒潮とメキシコ湾流の同期現象(Kohyama et al. 2021, Science) sites.google.com/site/tsubasako… リンク Wikipedia 円周率 円周率(えんしゅうりつ、英: Pi、独: Kreiszahl、中: 圓周率)とは、円の直径に対する円周の長さの比率のことをいい、数学定数の一つである。通常、円周率はギリシア文字である πに代表される。円の直径から円周の長さや円の面積を求めるときに用いる。また、数学をはじめ、物理学、工学といった科学の様々な理論の計算式にも出
-
-
三角関数や微積分の有用性に疑問を投げかける政治家の話があった。それに対して私のTwitterのタイムラインでは蜂の巣を突いたようにこれらの有用性や美しさを表明するツイートで溢れた。しかし同時に疑問を湧く、若者の時間は貴重だ。大学はその希少性を理解しているだろうか。 この難題を考えるために、ブライアン・カブランさんの本「教育反対の経済学」を読んだ。ちなみにこの本の価格が4800円と高いし、それに負けず中身もとてもボリューミーだ。 この本の中身を紹介する前に幾つかの前提をみなさんと共有しておきたい。経済学が前提のこの本で「役に立つ」というのはほとんどの場合は個人もしくは国家の収入が増えるという意味である。またこの本の著者及び私山本一成は大学というシステムで便益を受けている側であることも追記したい。 統計的に大学卒業者は高校卒業者より給料が高い。アメリカだとその傾向は先進国の中でもさらに顕著で最
-
可視化や統計でデータに『恣意的なストーリーを語らせる』16の闇の魔術【bad charts】 - Qiita
- 324 users
- qiita.com/Ringa_hyj
- テクノロジー
- 2020/12/03
闇の魔術に対する防衛術 Advent Calendar 2020の三日目 はじめに データの可視化は非常に難しい。 まずデータの抽出が難しい ・データソースごとの整合性が取れているか ・取得したデータとソースデータに欠損が生じていないか ・SQL文を実行したサマリの結果が部分的に抜け落ちていないか。 その確認は時間的にも精神的にも苦痛。 しかし、苦労して抽出したデータも使い方で全くの無駄になる その例として「可視化や統計」部分に着目してお話をしようと考えた。 データの背景を知らない人には、データ可視化が歩み寄る手段になるし、伝えたい事をインパクトを伴って伝えられるなど非常にメリットである。 ※ただし 「可視化」の使い方によっては誤った理解をさせることも可能。 伝えたい事だけを正しいように見せる方法もあり、 可視化に詳しくない人に誤解を与えて自分の主張を通すこともできるかもしれない。 これは
-
CSSの数学関数と言えば、calc()が便利ですよね。 しかし、便利な数学関数はcalc()だけではありません! 先月、Firefoxにサポートされたことにより、すべてのモダンブラウザにサポートされたCSSの比較関数「min()」「max()」「clamp()」の使い方を紹介します。 最大幅や最小幅を計算式で定義できる「min()」「max()」、フォントサイズの最小値と最大値をコの字のクランプのように計算式で定義できる「clamp()」、 これからのWebページやスマホアプリの実装にかなり役立つと思います。 Everything I Learned About min(), max(), clamp() In CSS by Ahmad Shadeed 下記は各ポイントを意訳したものです。 ※当ブログでの翻訳記事は、元サイト様にライセンスを得て翻訳しています。 はじめに CSSの比較関数の
-
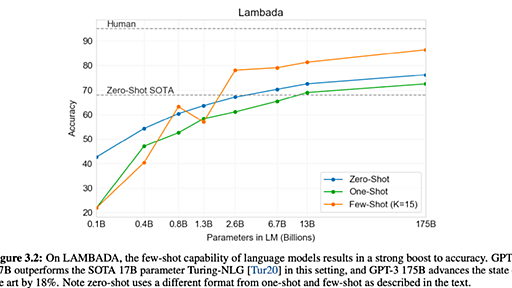
超巨大高性能モデルGPT-3の到達点とその限界. この記事では、超巨大言語モデルGPT-3の技術的な解説、GPT-3達成したことと… | by akira | Jul, 2020 | Medium
- 321 users
- medium.com/@akichan_f
- テクノロジー
- 2020/07/24
この記事についてこの記事ではGPT-3[1]の解説をします。内容のサマリは以下の通りです。 GPT-3の前身であるGPT-2では、巨大なデータセット+巨大なネットワークで言語モデルを構築し、各タスクで学習させなくても良い結果が得られた。GPT-3では、さらに巨大なデータセット+さらに巨大なネットワークで言語モデルを構築し、数十のサンプルを見せると凄く良い結果が得られた一方、様々なタスクに言語モデルのスケールアップのみで対応することへの限界が見えてきた。人種、性別、宗教などへの偏見の問題や、悪用に対する課題もある。この記事の流れは以下の通りです。 Transformer, GPT-2の説明GPT-3のコンセプトと技術的な解説GPT-3ので上手くいくタスクGPT-3で上手くいかないタスク偏見や悪用への見解 Transformerまず、GPT-3の前身となったGPT-2に入る前に、その中に使われ
-
統計学を哲学する « 名古屋大学出版会
- 319 users
- www.unp.or.jp
- 学び
- 2020/09/11
目 次 序 章 統計学を哲学する? 1 本書のねらい 2 本書の構成 第1章 現代統計学のパラダイム 1 記述統計 1-1 統計量 1-2 「思考の経済」としての記述統計 1-3 経験主義、実証主義と帰納の問題 2 推測統計 2-1 確率モデル 2-2 確率変数と確率分布 2-3 統計モデル 2-4 推測統計の世界観と「確率種」 第2章 ベイズ統計 1 ベイズ統計の意味論 2 ベイズ推定 2-1 仮説の確証と反証 2-2 パラメータ推定 2-3 予測 3 ベイズ統計の哲学的側面 3-1 帰納論理としてのベイズ統計 3-2 内在主義的認識論としてのベイズ統計 3-3 ベイズ主義の認識論的問題 3-4 小括:ベイズ統計の認識論的含意 第3章 古典統計 1 頻度主義の意味論 2 検定の考え方 2-1 蓋然的仮説の反証 2-2 仮説検定の考え方 2-3 検定の構成 2-4 サンプルサイズ 3 古典
-
数理最適化案件とAI/機械学習案件とのアナロジー 「やってみなければわからない」中で僕たちDSはどうするか本記事では表題に関して、脳筋系ゆるふわVTuberこと入社2年目DSの岡部がお送りいたします。(DS=データサイエンティスト) 発... ◆【理論・実践】(2021年時点で)オススメの参考書 最大のアップデートはこちらの2冊です。参考書は時代の流れに合わせていいものが出てくるものですね。もちろん過去の参考書にもいいものはたくさんありますが、日進月歩の分野である以上、新しいものに軍配が上がりやすい構図はあると思います。 しっかり学ぶ数理最適化 モデルからアルゴリズムまで Pythonではじめる数理最適化: ケーススタディでモデリングのスキルを身につけよう 以下それぞれの所感です 【理論】「最適化分野全般を知るための『最適解』」とも言われている教科書 僕が最適化にハマっていた当時は様々な本
-
みんな書いていないことを読み取りすぎ。 勝手に反語だと思ったり、脳内で補完していたり、単純に誤読していたり。 国語のテストで、書かれていることから正答を導き出す問題あるけど、あれってめっちゃ大事だったんだなぁって思う。 ちなみにうちの学校では国語ができないと英語の長文問題も、数学の文章題も読み解けないから、まずは国語を完璧にしろって言われていた。 「いや、普通に読めばわかるじゃん……」って思っていたけど、大事だったんだなぁ。 (追記) el-condor こういうことを主張している人が、ある政治勢力についてはその発言を徹底的に悪意に解釈しつつ反対勢力についてはその多数派の主張を無視してまで言葉通りに解釈しているのを見る時があって微笑ましい。 さっそく書いてないことを読み取る人が出てきたね。 (追記2) 「Aという主張をしている人は、Bという主張もする」は、Bと主張をしている文書への指摘じゃ
-
最適輸送の解き方
- 317 users
- www.slideshare.net/joisino
- テクノロジー
- 2021/06/17
最適輸送問題(Wasserstein 距離)を解く方法についてのさまざまなアプローチ・アルゴリズムを紹介します。 線形計画を使った定式化の基礎からはじめて、以下の五つのアルゴリズムを紹介します。 1. ネットワークシンプレックス法 2. ハンガリアン法 3. Sinkhorn アルゴリズム 4. ニューラルネットワークによる推定 5. スライス法 このスライドは第三回 0x-seminar https://sites.google.com/view/uda-0x-seminar/home/0x03 で使用したものです。自己完結するよう心がけたのでセミナーに参加していない人にも役立つスライドになっています。 『最適輸送の理論とアルゴリズム』好評発売中! https://www.amazon.co.jp/dp/4065305144 Speakerdeck にもアップロードしました: https
-
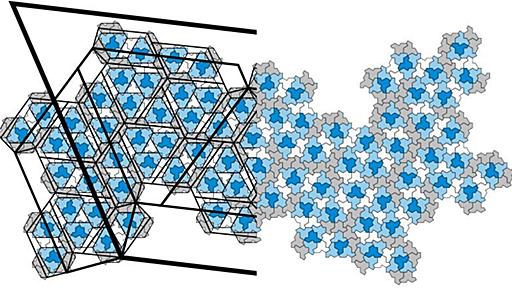
Innovative Tech: このコーナーでは、テクノロジーの最新研究を紹介するWebメディア「Seamless」を主宰する山下裕毅氏が執筆。新規性の高い科学論文を山下氏がピックアップし、解説する。Twitter: @shiropen2 英国の数学者らと、カナダのウォータールー大学と米アーカンソー大学に所属する研究者らが発表した論文「An aperiodic monotile」(プレプリント)は、繰り返しパターンを作らず、2次元の表面を無限に敷き詰めることができる単一のタイル形状を発見した研究報告である。 このような図形を非周期的なタイルと呼び、2次元の平面にタイルを隙間なく敷き詰めるが決して周期的ではない形状を指す。 非周期的なタイルの最初の集合は、1966年に発見された2万種類以上のタイルの組み合わせだった。その後、タイルの種類を減らす方向に研究が進んだ結果、最も有名な非周期的なタ
-
何でも微分する
- 313 users
- speakerdeck.com/joisino
- テクノロジー
- 2023/11/01
-
-
九九のドラマ性は異常
- 312 users
- anond.hatelabo.jp
- 学び
- 2021/11/16
-
-
超おもしろい古典制御の歴史。制御工学誕生のドラマとは!?
- 310 users
- controlabo.com
- エンタメ
- 2023/05/02
紀元前:水時計太古のフィードバック制御システムとして有名なのが、紀元前3世紀のギリシャで用いられていた水時計です。水時計は次のような機構で水を溜め、溜まった水の量で時間を計る装置です。 水が溜まるスピードを一定にするためには、1段目のタンクの水位を一定に保つ必要がありました。そのため三角錐型の「浮き」によって、下図のような機構で水の量が調整されていました。 この水時計、17世紀に振り子時計が登場するまでは、この世で最も精度のよい時計だったそうです。意外とすごいですね。 1788年:ワットの遠心調速機時は飛んで18世紀のイギリス。ここで制御工学の原点と言える装置が実用化されます。蒸気機関です。 蒸気機関は人類が初めて手にした原動機であり、産業革命をもたらしました。この蒸気機関の発展に多大な貢献をしたのが、ワット(Watt)です。 蒸気機関を産業利用するためには、生み出される回転の速度を一定に
-
アメリカ数学会で2人の10代の少女がピタゴラスの定理について新しい証明方法をプレゼンテーションしたことが話題になっています。応用数学の専門家であるキース・マクナルティ氏は「性別、民族、社会人口学的背景に関係なく、喜びと情熱があれば誰でも、研究分野での卓越性は達成可能であることを示す素晴らしい出来事」と評しているほか、その証明方法自体が波紋を呼んでいます。 Here’s How Two New Orleans Teenagers Found a New Proof of the Pythagorean Theorem | by Keith McNulty | Apr, 2023 | Medium https://keith-mcnulty.medium.com/heres-how-two-new-orleans-teenagers-found-a-new-proof-of-the-pytha
-
ピケティ『21世紀の資本』: r>g は格差の必要 or 十分条件か? - 山形浩生の「経済のトリセツ」
- 310 users
- cruel.hatenablog.com
- 政治と経済
- 2021/01/04
21世紀の資本 作者:トマ・ピケティ発売日: 2015/04/27メディア: Kindle版 新年仕事始め前の小ネタ。ツイッターでこんなのみかけたのよ。 このツイ主は、浅田論文を読んでおくことでどういう知見を得るべきなのか、ここで採りあげているネット番組の問題提起に対してそれがどう関係してくるのかは明記していない。けれど、文脈から判断して、これは日本で r>g が顕著になってきたことなんか重視すべきじゃない、それで格差なんか増えない、こんなんで騒ぐやつは煽りだ、と言いたいのだろうとぼくは判断する。 さて、この人がツイートないで言及している論文はこれだ。 core.ac.uk ちょっと待った、これ、COREか! ワタクシが座興で訳していたら「金払わないと訳しちゃダメ」と言ってそれを潰しやがった……まあいいや。勝手にやってたことだから仕方ないんだけど。が、閑話休題。 (なんか別物らしい。とばっ
新着記事
キーボードショートカット一覧
j次のブックマーク
k前のブックマーク
lあとで読む
eコメント一覧を開く
oページを開く