Descending, Lifting or Smoothing: Secrets of Robust Cost Optimization

Abstract

Robust cost optimization is the challenging task of fitting a large number of parameters to data points containing a significant and unknown fraction of outliers. In this work we identify three classes of deterministic second-order algorithms that are able to tackle this type of optimization problem: direct approaches that aim to optimize the robust cost directly with a second order method, lifting-based approaches that add so called lifting variables to embed the given robust cost function into a higher dimensional space, and graduated optimization methods that solve a sequence of smoothed cost functions. We study each of these classes of algorithms and propose improvements either to reduce their computational time or to make them find better local minima. Finally, we experimentally demonstrate the superiority of our improved graduated optimization method over the state of the art algorithms both on synthetic and real data for four different problems.

1 Introduction

Robust cost optimization aims to fit parameters to data containing outliers. This generic optimization problem arises in a large number of applications in computer vision such as bundle adjustment [23], optical flow [4], SLAM [8], registration of 3D surfaces [30], etc. In applications where the data contains a small number of outliers, using a convex kernel¹, such as the $L_1$ kernel or the Huber kernel, sufficiently reduces influence of outliers to obtain a good fit of the parameters to inlier data points. However, when the observations contain a large number of potentially gross outliers, a convex kernel is not “robust” enough and a quasi-convex kernel, such as Tukey’s biweight kernel, has to be employed. Optimizing over a sum of quasi-convex kernels produces a highly non-convex cost function with many local minima. In low-dimensional parameter problems poor local minima can be escaped using stochastic/sampling approaches, such as RANSAC [10] or simulated annealing [16]. Nevertheless, such methods are impractical for applications that have a large number of parameters and data points (such as bundle adjustment or optical flow). For these large scale problems deterministic second-order approaches are generally considered to be a good compromise between efficiency and accuracy. In return, special care must be taken to escape poor local minima.

Contributions: In this paper, we start with identifying three classes of such algorithms: direct approaches, lifting-based approaches and graduated optimization methods. Then, we study each of these classes of algorithms and propose improvements either to reduce their computational time or to make them find better local minima. More precisely, we make the following contributions: (i) We show that the direct approaches only differ in their quadratic approximation of the quasi-convex kernel. This analysis allows us to outline the limitations and numerical instabilities of some of these algorithms. (ii) We propose to use a convexified Newton approximation to implement lifting-based approaches and experimentally demonstrate that this modification leads to better local minima than the classical Gauss-Newton approximation. (iii) We design a novel stopping criterion that allows to significantly speed-up graduated optimization methods without harming their ability to avoir poor local minima. (iv) We experimentally demonstrate the superiority of our improved graduated optimization method over the state of the art algorithms both on synthetic and real data for three different problems.

Organization of the Paper: The rest of the paper is organized as follows: Sect. 2 discusses the related work and Sect. 3 introduces our notations as well as some fundamental definitions. Our contributions are gathered in Sects. 4, 5 and 6, where we study three different types of algorithms and make several recommendations to improve their performances. In Sect. 7 numerical evaluations of the methods discussed in the previous three sections are presented. A summary of our recommendations and future work are provided in Sect. 8.

2 Related Work

In this section, we describe the state of the art approaches for robust cost optimization (e.g. redescending m-estimation [15]) and how they are related to the novel method we propose in this paper. We focus on deterministic second-order methods because they are generally considered to be a good compromise between efficiency and accuracy for problems with large numbers of parameters and data points (such as bundle adjustment). In the following literature review we distinguish direct approaches, graduated optimization methods and lifting-based approaches².

Direct approaches aim to optimize the original robust objective, usually by utilizing a surrogate model suitable for a second-order method. IRLS [13], the Triggs correction [23] and “square rooting the kernel” [9] are well-known instances of this class of methods. Consequently, these approaches find the local minimum corresponding to the basin of convergence they were initialized in.

Graduated optimization is a meta-algorithm explicitly designed to avoid poor local minima by building a sequence of successively smoother (and therefore easier to optimize) approximations of the original objective. The optimization algorithm consists in successively optimizing the sequence of cost functions (e.g. by using one of the direct approaches), with the solution from the previous objective used as starting point for the next one. Homotopy optimization methods (e.g. [7]) and continuation methods (e.g. [20]) are other terms for the same meta-algorithm. Graduated non-convexity [5], multi-scale methods and Gaussian homotopies [19], and deterministic annealing (e.g. [21]) are specific constructions that belong to this family of methods. One drawback of graduated optimization is that they appear to be inefficient as an entire sequence of optimization problems has to be solved.

Instead of explicitly building a sequence of smoothed cost functions, lifting approaches³ [26, 29, 31] add so called lifting variables (which can be interpreted as confidence weights) to embed the original robust cost function into a higher dimensional space of unknowns. Initializing the lifting variables to a large value corresponds to smoothing the robust cost function while setting them to their optimal values produces the original robust cost function. The algorithm consists in jointly optimizing over the parameters of interest and the lifting variables. Lifting-based methods can be interpreted as “self-tuned” graduated optimization. One drawback of these methods is, that their performance significantly depends on the initialization of the lifting variables (as demonstrated in our numerical experiments).

3 Background and Notations

Robust cost optimization consists in minimizing functions of the form:

$$\begin{aligned} {\min _{\varvec{\theta }} \; \varPsi (\varvec{\theta })\qquad \text {with}\qquad \varPsi (\varvec{\theta })=\sum _{i=1}^{N}\psi (||\mathbf {f}_i(\varvec{\theta })||),} \end{aligned}$$

(1)

where $\varvec{\theta }\in \mathbb {R}^p$ are the parameters of interest, $\mathbf {f}_i(\varvec{\theta }):\mathbb {R}^p\rightarrow \mathbb {R}^d$ is the i-th vectorial residual function and $\psi \left( \cdot \right)$ is a robust kernel function (that will be formally defined hereinafter), that allows to reduce the influence of outlying data points. $||\cdot ||$ is the usual $L_2$-norm (leading to isotropic penalization of large residuals). The arguably simplest application of Eq. (1) arises when robustly fitting a “mean” vector $\varvec{\theta }$ to data points $\mathbf {y}_i\in \mathbb {R}^d$ which leads to the following problem: $\min _{\varvec{\theta }} \sum _{i=1}^{N}\psi \left( ||\mathbf {y}_i-\varvec{\theta }||\right)$. From a practical point of view, we would like a robust kernel function to convey the idea that large residuals should always have a smaller influence than smaller residuals when estimating the optimal parameters $\varvec{\theta }^*$. We will now translate this idea into formal properties of a robust kernel function: A robust kernel function $\psi : \mathbb {R} \rightarrow \mathbb {R}_0^+$ is a symmetric function sufficiently smooth near 0 with the following properties: (1) $\psi (0)=0$ and $\psi ''(0) = 1$. (2) The mapping $\phi : \mathbb {R}_0^+ \rightarrow \mathbb {R}_0^+$ with $\phi (z) := \psi (\sqrt{2z})$ (or $\phi (r^2/2) = \psi (r)$) is concave and monotonically increasing.

In robust cost functions such as Eq. 1 the robust kernel $\psi$ is applied only to non-negative arguments, but it is customary to extend its domain to the entire real line $\mathbb {R}$. The “normalization” property (property 1) allows to compare the robustness of different kernels. Concerning property 2, the fact that $\phi$ should be monotonically increasing is obvious but the necessity of its concavity requires some justification. To so do, we examine the weight function $\omega$ associated with a robust kernel $\psi$ that describes how $\psi$ weighs the influence of residuals⁴:

$$\begin{aligned} \omega (r)&:= \psi '(r)/r = \phi '(r^2/2). \end{aligned}$$

(2)

Since we aim for large residuals having a smaller influence than smaller residuals, $\omega (\cdot )$ should be monotonically decreasing in |r|, which is guaranteed by the concavity of $\phi$. Let us note that this definition of a robust kernel includes both convex and quasi-convex kernels. However, as stated in the introduction, in the experiments we will only consider quasi-convex kernels.

4 Direct Methods: IRLS, Triggs Correction, $\sqrt{\psi }$

In this section, we review the approaches that aim to (iteratively) minimize the objective $\varPsi (\varvec{\theta })$ (see Eq. 1) without explicitly modifying the objective, and we outline that each of these approaches can be interpreted as methods trying to locally approximate $\psi$ with a quadratic function. In order to be computationally efficient, these methods try to cast the original problem in a way that allows non-linear least-squares solvers, such as Gauss-Newton or Levenberg-Marquardt, to be employed. As a consequence, at each iteration these approaches perform the following steps:

• 1. perform a first order approximation of the vectorial residual function around the current value of the parameters $\varvec{\theta }=\bar{\varvec{\theta }}$: $\mathbf {f}_i(\bar{\varvec{\theta }}+\varDelta \varvec{\theta }) \approx \bar{\mathbf {f}}_i + \mathtt {J}_i \varDelta \varvec{\theta }$ where $\mathtt {J}_i$ is the Jacobian of $\mathbf {f}_i(\bar{\varvec{\theta }}+\varDelta \varvec{\theta })$ w.r.t. the increment $\varDelta \varvec{\theta }$ evaluated at $\varDelta \varvec{\theta }=\mathbf {0}$ and $\bar{\mathbf {f}}_i$ is a short hand notation for $\mathbf {f}_i(\bar{\varvec{\theta }})$,

• 2. approximate $\psi (||\bar{\mathbf {f}}_i\!+\!\mathtt {J}_i\varDelta \varvec{\theta })||)$ with a quadratic function $\breve{\psi }$ s.t. $\psi (|| \bar{\mathbf {f}}_i||)=\breve{\psi }(|| \bar{\mathbf {f}}_i||)$.

While step 1 is the same for all the approaches, step 2 turns out to be very different for each of them.

IRLS [13]: One way to derive the IRLS methods is to interpret it as instance of the majorize-minimize principle (e.g. [17]): given the current solution $\bar{\varvec{\theta }}$, IRLS uses a quadratic majorizer of $\psi$, i.e $\psi (r) \le \breve{\psi }_{\text {IRLS}}(r)$:

$$\begin{aligned} \breve{\psi }_{\text {IRLS}}(||\bar{\mathbf {f}}_i + \mathtt {J}_i\varDelta \varvec{\theta })||) = \omega (|| \bar{\mathbf {f}}_i||) \left( ||\bar{\mathbf {f}}_i + \mathtt {J}_i\varDelta \varvec{\theta })||^2/2 -||\bar{\mathbf {f}}_i||^2/2\right) + \psi (|| \mathbf {f}_i(\bar{\varvec{\theta }})||). \end{aligned}$$

(3)

Since robust kernels are by construction sub-quadratic, a non-degenerate quadratic majorizer always exists. The IRLS algorithm iteratively builds and minimizes the quadratic surrogates, which yields a sequence of solutions $\varvec{\theta }^{(k)}$ with monotonically decreasing costs $\varPsi (\varvec{\theta }^{(k)})$.

Triggs Correction [23]: Contrary to IRLS, the Triggs correction performs a second order expansion of $F_i(\varDelta \varvec{\theta }) := \phi (||\mathbf {f}_i + \mathtt {J}_i\varDelta \varvec{\theta }||^2/2)$ around $\varDelta \varvec{\theta }=\mathbf {0}$. The resulting approximation of $\psi$ is given by

$$\begin{aligned} \breve{\psi }_{\text {Triggs}}(||\bar{\mathbf {f}}_i + \mathtt {J}_i\varDelta \varvec{\theta })||) = \psi (|| \bar{\mathbf {f}}_i||) + \nabla _{\varDelta \varvec{\theta }} F_i(\mathbf {0})^\top \varDelta \varvec{\theta }+ \varDelta \varvec{\theta }^\top \mathtt {H}_{F_i}(\mathbf {0}) \varDelta \varvec{\theta } \end{aligned}$$

(4)

with the following expressions for the gradient and Hessian at $\varDelta \varvec{\theta }=\mathbf {0}$:

$$\begin{aligned} \nabla _{\varDelta \varvec{\theta }} F_i(\mathbf {0})&= \omega ({||\mathbf {f}_i||}) \mathtt {J}_i^\top \mathbf {f}_i&\mathtt {H}_{F_i}(\mathbf {0})&= \mathtt {J}_i^\top \left( \frac{\omega '(||\mathbf {f}_i||)}{||\mathbf {f}_i||} \mathbf {f}_i \mathbf {f}_i^\top + \omega (||\mathbf {f}_i||) \mathtt {I}\right) \mathtt {J}_i. \end{aligned}$$

where we used Eq. 2 as well as $\phi ''(z) = (\omega (\sqrt{2z}))' = \frac{\omega '(\sqrt{2z})}{\sqrt{2z}}$. Note that $\mathbf {f}_i$ is an eigenvector for $\frac{\omega '}{||\mathbf {f}_i||} \mathbf {f}_i \mathbf {f}_i^\top + \omega \mathtt {I}$ (omitting arguments to $\omega$ and $\omega '$):

$$\begin{aligned} \left( \frac{\omega '}{||\mathbf {f}_i||} \mathbf {f}_i \mathbf {f}_i^\top + \omega \mathtt {I}\right) \mathbf {f}_i&= \omega ' ||\mathbf {f}_i|| \mathbf {f}_i + \omega \mathbf {f}_i = (\omega ' ||\mathbf {f}_i|| + \omega ) \mathbf {f}_i. \end{aligned}$$

Hence, if $\omega + ||\mathbf {f}_i|| \omega ' < 0$, then $\mathtt {H}_{F_i}(\mathbf {0})$ is negative-definite and the Triggs correction approach cannot be applied. The popular Ceres solver [1], which supports the Triggs correction for robust cost optimization, reverts to IRLS for the current step in this case.

Square-Rooting $\psi$ [9]: A third option consists in square-rooting $\psi$ and performing a first order Taylor expansion of it around $\varDelta \varvec{\theta }=\mathbf {0}$. Defining $G_i(\varDelta \varvec{\theta }) := g(\bar{\mathbf {f}}_i + \mathtt {J}_i\varDelta \varvec{\theta })$ where $g(\mathbf {v}) = \sqrt{\psi (||\mathbf {v}||)} \cdot \mathbf {v}/||\mathbf {v}||$, we obtain:

$$\begin{aligned} \breve{\psi }_{\sqrt{\,}}(||\bar{\mathbf {f}}_i + \mathtt {J}_i\varDelta \varvec{\theta })||) = \left( g({\bar{\mathbf {f}}_i)} + J_{G_i}(\mathbf {0})\varDelta \varvec{\theta }\right) ^2 \end{aligned}$$

(5)

with

$$\begin{aligned} \mathtt {J}_{G_i}(\mathbf {0}) = \mathtt {J}_{g_i}(\bar{\mathbf {f}_i})\mathtt {J}_i \quad \text {and}\quad \mathtt {J}_{g_i}(\mathbf {v}) = \frac{\sqrt{\psi (||\mathbf {v}||)} ||\mathbf {v}||^2 I - \frac{\gamma (\omega (\mathbf {v}))}{\sqrt{\psi (||\mathbf {v}||)}} \mathbf {v} \mathbf {v}^\top }{||\mathbf {v}||^3}. \end{aligned}$$

where we defined $\gamma (\omega (\mathbf {v})) = \psi (\mathbf {v}) - \omega (\mathbf {v}) \frac{||\mathbf {v}||^2}{2}$ (more details about that function $\gamma$ will be provided in Sect. 5). Despite $||\mathbf {v}||$ appearing in the denominator, $g(\mathbf {v})$ is smoothly behaving near $\mathbf {0}$. The $\mathbf {v}/||\mathbf {v}||$ term cancels out the non-differentiability induced by the square root. Observe that $\sqrt{\psi (||\mathbf {v}||)}$ behaves like $||\mathbf {v}||/\sqrt{2}$ near $\mathbf {v}=\mathbf {0}$, hence $g(\mathbf {v}) \approx \mathbf {v}/\sqrt{2}$ for $\mathbf {v} \approx \mathbf {0}$. Consequently, $\lim _{\mathbf {v} \rightarrow \mathbf {0}} \mathtt {J}_{g_i}(\mathbf {v}) = \mathtt {I}/\sqrt{2}$.

In Fig. 1, we plot the different approximations of ${\psi (||\bar{\mathbf {f}}_i + J_i(\bar{\varvec{\theta }})\varDelta \varvec{\theta })||)}$ for the 1-D linear function $f_i(\theta )=\theta$ and $\bar{\theta }=1$. One can see that both “Square-rooting $\psi$” and the Triggs correction do not preserve the symmetry of $\psi$, whereas IRLS does. Moreover, the IRLS approximation is the only function that has its minimum at 0 whereas “Square-rooting $\psi$” has a tendency to overshoot with a minimum at $\approx -0.7$ and the Triggs correction produces a negative second-order derivative.

Contribution: Our analysis shows that the underlying quadratic models are very different and that the IRLS model has desirable properties which supports what is pointed out in [29]: the Triggs correction performs poorly and “Square-rooting $\psi$” is often inferior to IRLS. Nevertheless, the direct approaches have a major drawback: their limited ability to escape poor local minima. This leads us to studying fundamentally different approaches in the following sections.

Fig. 1.

Quadratic surrogate models used by direct approaches at $\bar{\theta }=1$ (the x-axis corresponds to $\theta =\bar{\theta }+\varDelta \theta$): IRLS (Eq. 3), second order expansion used in the Triggs correction (Eq. 4) (which is concave at $\bar{\theta }$) and “Square-rooting $\psi$” (Eq. 5). Observe that only the IRLS model preserves the symmetry of $\psi$ and has its minimum at the zero residual.

5 Half-Quadratic Lifting-Based Methods

In this section we review the lifting approach for robust cost minimization proposed in [29], and we unify the formulation with a convexified Newton approximation⁵. In analogy with half-quadratic lifting [11] the robust kernel $\psi$ is reformulated as point-wise minimum over a family of convex parabolas,

$$\begin{aligned} \psi (x)&= \min _{v \in [0,1]} v \frac{x^2}{2} + \gamma (v), \end{aligned}$$

(6)

where $\gamma :[0,1] \rightarrow \mathbb {R}_0^+$ is a convex and monotonically decreasing “bias” function in [0, 1]. For many interesting choices of $\psi$ the bias function $\gamma$ can be continuously extended to the domain $\mathbb {R}_0^+$ (see e.g. [26]). $\gamma$ is convex but generally increasing in $\mathbb {R}_{\ge 1}$. In order to avoid the constraint $v \in [0,1]$ (or $v \ge 0$, respectively) we reparametrize $v=w(u)$, where $w:\mathbb {R} \rightarrow [0,1]$ or $w:\mathbb {R} \rightarrow \mathbb {R}_0^+$. Three sensible choices for w are $w(u)=u^2$, $w(u)=e^u$ and $w=\mathrm {sigmoid}(u)$, where $\mathrm {sigmoid}$ is the sigmoid function, e.g. $\mathrm {sigmoid}(u) = 1/(1+e^{-u})$. Note that in the objective Eq. 1 one has to introduce an auxiliary unknowns $u_i$ for each term in the sum, but this only induces a moderate increase in run-time in a second order minimization method (e.g. by leveraging the Schur complement [29]).

Using Eq. 6 we can reformulate Eq. 1 as

$$\begin{aligned} \varPsi (\varvec{\theta })&= \min _{u_1, \cdots , u_N} \sum _i \left( w(u_i) \frac{||\mathbf {f}_i(\varvec{\theta })||^2}{2} + \gamma (w(u_i)) \right) =: \min _{u_1, \cdots , u_N} \tilde{\varPsi }(\varvec{\theta }, (u_i)_i) \end{aligned}$$

(7)

For notational brevity we will write $w_i$ for $w(u_i)$, $w_i'$ for $w'(u_i)$ etc. in the following.

Gauss-Newton: After linearizing the residual $\mathbf {f}_i(\bar{\varvec{\theta }}+\varDelta \varvec{\theta }) \approx \bar{\mathbf {f}}_i + \mathtt {J}_i \varDelta \varvec{\theta }$ we can rewrite each term of $\tilde{\varPsi }$ as

(8)

After taking first order derivatives we obtain the Gauss-Newton model for $\tilde{\varPsi }$,

$$\begin{aligned} \tilde{\varPsi }^{GN}(\varDelta \varvec{\theta }, (\varDelta u_i)_i)&= \frac{1}{2} \sum _i \begin{pmatrix} \varDelta \varvec{\theta }\\ \varDelta u_i \end{pmatrix}^\top \begin{pmatrix} w_i \mathtt {J}_i^\top \mathtt {J}_i &{} \frac{w_i'}{2} \mathtt {J}_i^\top \bar{\mathbf {f}}_i \\ \frac{w_i'}{2} \bar{\mathbf {f}}_i^\top \mathtt {J}_i &{} \frac{(w_i')^2}{4w_i} ||\bar{\mathbf {f}}_i||^2 + \frac{(w_i'\gamma _i')^2}{2\gamma _i} \end{pmatrix} \begin{pmatrix} \varDelta \varvec{\theta }\\ \varDelta u_i \end{pmatrix} \nonumber \\&+ \sum _i \begin{pmatrix} w_i \mathtt {J}_i^\top \bar{\mathbf {f}}_i \\ \frac{w_i'}{2} ||\bar{\mathbf {f}}_i||^2 + w_i' \gamma _i' \end{pmatrix}^\top \begin{pmatrix} \varDelta \varvec{\theta }\\ \varDelta u_i \end{pmatrix} + const. \end{aligned}$$

(9)

By construction the matrices

$$\begin{aligned} \begin{pmatrix} w_i \mathtt {J}_i^\top \mathtt {J}_i &{} \frac{w_i'}{2} \mathtt {J}_i^\top \bar{\mathbf {f}}_i \\ \frac{w_i'}{2} \bar{\mathbf {f}}_i^\top \mathtt {J}_i &{} \frac{(w_i')^2}{4w_i} ||\bar{\mathbf {f}}_i||^2 + \frac{(w_i'\gamma _i')^2}{2\gamma _i} \end{pmatrix} \end{aligned}$$

(10)

are positive semi-definite. The bottom right element has two problematic points: when $w_i\rightarrow 0$ (then $(w_i')^2/w_i$ is indeterminate) and when $w_i\rightarrow 1$ (in this case $(\gamma _i')^2/\gamma _i$ is indeterminate as $\gamma (1)=0$). It can be shown [27] that the first order Taylor expansions of $(w')^2/w$ and $(\gamma '(v))^2/\gamma (v)$ at the problematic points are given by

$$\begin{aligned} \frac{(w'(\varDelta u))^2}{w(\varDelta u)}&\approx 2w''(0) + \tfrac{4}{3} w'''(0) \varDelta u&\frac{(\gamma '(1+\varDelta v))^2}{\gamma (1+\varDelta v)}&\approx 2\gamma ''(1) + \tfrac{4}{3} \gamma '''(1) \varDelta v \end{aligned}$$

for $\varDelta u$ and $\varDelta v$ small. Consequently, a Gauss-Newton based method can be implemented generically by providing $\gamma$ and w and the corresponding derivatives.

Newton: The Newton approximation of $F_i$ (Eq. 8) around $\bar{\varvec{\theta }}$ and $u_i$ is given by

$$\begin{aligned} F_i^N(\varDelta \varvec{\theta }, \varDelta u_i)&\approx \frac{1}{2} \begin{pmatrix} \varDelta \varvec{\theta }\\ \varDelta u_i \end{pmatrix}^\top \begin{pmatrix} w_i \mathtt {J}_i^\top \mathtt {J}_i &{} w_i' \mathtt {J}_i^\top \bar{\mathbf {f}}_i \\ w_i' \bar{\mathbf {f}}_i^\top \mathtt {J}_i &{} \frac{w_i''}{2} ||\bar{\mathbf {f}}_i||^2 + w_i'' \gamma _i' + (w_i')^2 \gamma _i'' \end{pmatrix} \begin{pmatrix} \varDelta \varvec{\theta }\\ \varDelta u_i \end{pmatrix} \nonumber \\&+\,\begin{pmatrix} w_i \mathtt {J}_i^\top \bar{\mathbf {f}}_i \\ \frac{w_i'}{2} ||\bar{\mathbf {f}}_i||^2 + w_i' \gamma _i' \end{pmatrix} \begin{pmatrix} \varDelta \varvec{\theta }\\ \varDelta u_i \end{pmatrix} + const. \end{aligned}$$

(11)

In this case the Hessian matrices

$$\begin{aligned} A_i^N := \begin{pmatrix} w_i \mathtt {J}_i^\top \mathtt {J}_i &{} w_i' \mathtt {J}_i^\top \bar{\mathbf {f}}_i \\ w_i' \bar{\mathbf {f}}_i^\top \mathtt {J}_i &{} \frac{w_i''}{2} ||\bar{\mathbf {f}}_i||^2 + w_i'' \gamma _i' + (w_i')^2 \gamma _i'' \end{pmatrix} =: \begin{pmatrix} w_i \mathtt {J}_i^\top \mathtt {J}_i &{} w_i' \mathtt {J}_i^\top \bar{\mathbf {f}}_i \\ w_i' \bar{\mathbf {f}}_i^\top \mathtt {J}_i &{} \alpha _i \end{pmatrix} \end{aligned}$$

(12)

are not guaranteed to be p.s.d. We also denote the bottom right element of $A_i^N$ by $\alpha _i := \frac{w_i''}{2} ||\bar{\mathbf {f}}_i||^2 + w_i'' \gamma _i' + (w_i')^2 \gamma _i''$. Assuming that $w_i \mathtt {J}_i^\top \mathtt {J}_i$ is strictly positive definite (not just p.s.d. guaranteed by construction)⁶, we obtain via the Schur complement that $A_i^N$ is p.s.d. iff $\alpha _i - \frac{(w_i)'^2}{w_i} \bar{\mathbf {f}}_i^\top \mathtt {J}_i (\mathtt {J}_i^\top \mathtt {J}_i)^{-1} \mathtt {J}_i^\top \bar{\mathbf {f}}_i \ge 0$. In order to enforce that $A_i^N$ is p.s.d., we add a non-negative value $\delta _i$ to $\alpha _i$

$$\begin{aligned} \alpha _i + \delta _i - \frac{(w_i)'^2}{w_i} \bar{\mathbf {f}}_i^\top \mathtt {J}_i (\mathtt {J}_i^\top \mathtt {J}_i)^{-1} \mathtt {J}_i^\top \bar{\mathbf {f}}_i \ge 0. \end{aligned}$$

(13)

Since $\mathtt {J}_i (\mathtt {J}_i^\top \mathtt {J}_i)^{-1} \mathtt {J}_i^\top$ is a projection matrix into a respective subspace (the column space of $\mathtt {J}_i$), we deduce that $\bar{\mathbf {f}}_i^\top \mathtt {J}_i (\mathtt {J}_i^\top \mathtt {J}_i)^{-1} \mathtt {J}_i^\top \bar{\mathbf {f}}_i \le ||\bar{\mathbf {f}}_i||^2$. Hence, setting $\delta _i = \max \{ 0, \frac{(w_i)'^2}{w_i} ||\bar{\mathbf {f}}_i||^2 - \alpha _i \}$ is a sufficient condition for Eq. 13 to be satisfied. Note that $\alpha _i + \delta _i = \max \big \{ \alpha _i, \frac{(w_i)'^2}{w_i} ||\bar{\mathbf {f}}_i||^2 \big \}$ and therefore the convexified matrix $\breve{A}_i^N$ is given by

$$\begin{aligned} \breve{A}_i^N := \begin{pmatrix} w_i \mathtt {J}_i^\top \mathtt {J}_i &{} w_i' \mathtt {J}_i^\top \bar{\mathbf {f}}_i \\ w_i' \bar{\mathbf {f}}_i^\top \mathtt {J}_i &{} \;\max \left\{ \alpha _i, \frac{(w_i)'^2}{w_i} ||\bar{\mathbf {f}}_i||^2 \right\} \end{pmatrix}. \end{aligned}$$

(14)

Thus, the (convexified) Newton model for $\tilde{\varPsi }$ finally reads as

$$\begin{aligned} \tilde{\varPsi }^N(\varDelta \varvec{\theta }, (\varDelta u_i)_i)&= \frac{1}{2} \sum _i \begin{pmatrix} \varDelta \varvec{\theta }\\ \varDelta u_i \end{pmatrix}^\top \begin{pmatrix} w_i \mathtt {J}_i^\top \mathtt {J}_i &{} w_i' \mathtt {J}_i^\top \bar{\mathbf {f}}_i \\ w_i' \bar{\mathbf {f}}_i^\top \mathtt {J}_i &{} \;\max \left\{ \alpha _i, \frac{(w_i)'^2}{w_i} ||\bar{\mathbf {f}}_i||^2 \right\} \end{pmatrix} \begin{pmatrix} \varDelta \varvec{\theta }\\ \varDelta u_i \end{pmatrix} \nonumber \\&+ \sum _i \begin{pmatrix} w_i \mathtt {J}_i^\top \bar{\mathbf {f}}_i \\ \frac{w_i'}{2} ||\bar{\mathbf {f}}_i||^2 + w_i' \gamma _i' \end{pmatrix}^\top \begin{pmatrix} \varDelta \varvec{\theta }\\ \varDelta u_i \end{pmatrix} + const. \end{aligned}$$

(15)

Contribution: Our novel Newton-based approach (Eq. 15) suggests different updates for $\varDelta \varvec{\theta }$ and $(\varDelta u_i)_{i=1,\cdots ,N}$ than the Gauss-Newton approach (Eq. 9). This is due to the fact that our Newton-based solver leverages second order information. Thus one may expect it to reach better local minima than the Gauss-Newton based solver.

6 Graduated Optimization

Graduated optimization aims to avoid poor local minima usually returned by local optimization methods (such as the direct methods presented in Sect. 4) by iteratively optimizing successively better approximations of the original objective. It therefore relies on a sequence of objectives $(\varPsi ^0, \cdots , \varPsi ^{k_{\max }})$ such that $\varPsi ^0 = \varPsi$ and $\varPsi ^{k+1}$ is in some sense easier to optimize than $\varPsi ^k$. To our knowledge graduated optimization has not been explored much in the geometric computer vision literature (besides graduated non-convexity, which was specifically developed for a robust and edge-preserving image smoothing method), although it is frequently used in image matching (by leveraging a scale space or image pyramid e.g. [18, 24]). Algorithm 1 illustrates the basic graduated optimization method. The construction of $\varPsi ^k$ and the choices for a stopping criterion are left unspecified and will be described in the following.

Choice of $\varPsi ^k$: For robust costs the natural approach to construct the sequence $(\varPsi ^0, \cdots , \varPsi ^{k_{\max }})$ is by appropriate scaling of the kernels. Let $(s_k)_{k=0}^{k_{\max }}$ be a sequence of scaling parameters with $s_0 = 1$ and $s_k < s_{k+1}$. Define

$$\begin{aligned} \psi ^k(r) := s_k^2 \psi (r/s_k) \quad \qquad \text {and} \quad \qquad \varPsi ^k(\varvec{\theta }) := \sum \nolimits _i \psi ^k(||\mathbf {f}_i(\varvec{\theta })||). \end{aligned}$$

(16)

In most cases one will choose $s_k = \tau ^k$ for a user-specified value $\tau$ (a typical choice also used in our experiments is $\tau =2$). Due to the following lemma this construction of $(\varPsi ^k)_{k=0}^{k_{\max }}$ is not only natural, but also has a solid justification:

Lemma 1

Let $\psi$ be a robust kernel and $s \ge 1$. The following statements hold:

• 1. $\psi (r/s) \le \psi (r) \le s^2\psi (r/s)$ for all r.

• 2. Let $0 \le r' \le r$. Then we have inequality $\psi (r) - \psi (r') \le s^2\big ( \psi (r/s) - \psi (r'/s) \big )$.

Proof

$\psi (r/s) \le \psi (r)$ follows from monotonicity of $\psi$ and that $r/s \le r$ for $s \ge 1$, yielding one part of the first claim. Since $\psi$ is a robust kernel, then the associated mapping $\phi (z) = \psi (\sqrt{2z})$ is concave and monotonically increasing in its domain $\mathbb {R}_0^+$. Further, $\psi$ is normalized such that $\psi (0) = \phi (0) = 0$. From the concavity of $\phi$ we deduce that

$$\begin{aligned} \phi (\alpha z) = \phi \big ( \alpha z + (1-\alpha )\cdot 0 \big ) \ge \alpha \phi (z) + (1-\alpha ) \phi (0) = \alpha \phi (z) \end{aligned}$$

for all $\alpha \in [0,1]$. Now set $\alpha = 1/s^2$ for $s\ge 1$, and we obtain

$$\begin{aligned} \phi (z/s^2) = \psi (\sqrt{2z}/s) \ge \phi (z)/s^2 = \psi (\sqrt{2z})/s^2. \end{aligned}$$

Substituting $z=r^2/2$ (or $r = \sqrt{2z}$) yields $\psi (r/s) \ge \psi (r)/s^2$ or equivalently $s^2 \psi (r/s) \ge \psi (r)$. This proves the first claim.

The inequality in the second claim is equivalent to $s^2 \psi (r'/s) - \psi (r') \le s^2 \psi (r/s) - \psi (r)$. The function $d(r) := s^2 \psi (r/s) - \psi (r) \ge 0$ is monotonically increasing, since $d'(r) = s \psi '(r/s) - \psi '(r) = r (\omega (r/s) - \omega (r)) \ge 0$ (as $\omega$ is monotonically decreasing). This verifies the second claim.

The first statement implies that $\varPsi ^{k}(\varvec{\theta }) \le \varPsi ^{k+1}(\varvec{\theta })$ for all $\varvec{\theta }$, and optimizing $\varPsi ^k$ means that an upper bound of $\varPsi ^0 = \varPsi$ is minimized.⁷ The second statement in the lemma shows that $\varPsi ^k$ is in a certain sense easier than $\varPsi ^\ell$ for $\ell < k$: if $\bar{\varvec{\theta }}$ and $\varvec{\theta }^+$ are solutions such that $||\mathbf {f}_i(\varvec{\theta }^+)|| \le ||\mathbf {f}_i(\bar{\varvec{\theta }})||$ for all i (i.e. going from $\bar{\varvec{\theta }}$ to $\varvec{\theta }^+$ decreases all residuals), then $\varPsi ^\ell (\bar{\varvec{\theta }}) - \varPsi ^\ell (\varvec{\theta }^+) \le \varPsi ^k(\bar{\varvec{\theta }}) - \varPsi ^k(\varvec{\theta }^+)$. Thus, $\varPsi ^k$ is not only an upper bound of $\varPsi ^{k-1}$, but also tends to be steeper.

Stopping Criterion: We propose to utilize a relative stopping criterion. Let $\bar{\varvec{\theta }}$ be the current solution and $\varvec{\theta }^+ := \bar{\varvec{\theta }} + \varDelta \varvec{\theta }$ be a new solution. Define

$$\begin{aligned} \mathcal{I}_> := \left\{ i: \mathbf {f}_i(\varvec{\theta }^+) > \mathbf {f}_i(\bar{\varvec{\theta }}) \right\} , \end{aligned}$$

(17)

i.e. $\mathcal{I}_>$ indexes the strictly increasing residuals after updating the solution. Further, let

$$\begin{aligned} \varPsi ^k_>(\varvec{\theta }) := \sum \nolimits _{i \in \mathcal{I}_>} \psi ^k(\mathbf {f}_i(\varvec{\theta })) \qquad \qquad \varPsi ^k_\le (\varvec{\theta }) := \sum \nolimits _{i \notin \mathcal{I}_>} \psi ^k(\mathbf {f}_i(\varvec{\theta })) \end{aligned}$$

(18)

(analogously we introduce $\varPsi ^{k-1}_\le (\varvec{\theta })$ and $\varPsi ^{k-1}_>(\varvec{\theta })$). We have $\varPsi ^k(\varvec{\theta }) = \varPsi ^k_\le (\varvec{\theta }) + \varPsi ^k_>(\varvec{\theta })$ by construction, and $\varPsi ^\ell _>(\bar{\varvec{\theta }}) \le \varPsi ^\ell _>(\varvec{\theta }^+)$ and $\varPsi ^\ell _\le (\varvec{\theta }^+) \le \varPsi ^\ell _\le (\bar{\varvec{\theta }})$ for all $\ell \in \{0,\cdots , k_{\max }\}$. We also introduce

$$\begin{aligned} \varDelta ^\ell _\le := \varPsi ^\ell _\le (\bar{\varvec{\theta }}) - \varPsi ^\ell _\le (\varvec{\theta }^+) \ge 0 \quad \quad \text {and} \quad \quad \varDelta ^\ell _> := \varPsi ^\ell _>(\varvec{\theta }^+) - \varPsi ^\ell _>(\bar{\varvec{\theta }}) \ge 0 \end{aligned}$$

(19)

for all $\ell \in \{0,\cdots ,k_{\max }\}$ (note the different positions of $\bar{\varvec{\theta }}$ and $\varvec{\theta }^+$ in $\varDelta ^\ell _\le$ and $\varDelta ^\ell _>$). Now if $\bar{\varvec{\theta }}$ is close to a stationary point of $\varPsi ^k$, then $\varDelta ^k_\le \approx \varDelta ^k_>$. Since $\varvec{\theta }^+$ is assumed to improve $\varPsi ^k$, we read $\varDelta ^k_\le \ge \varDelta ^k_>0$ and therefore $\varDelta ^k_\le - \varDelta ^k_> \le \bar{\eta }$ (for a small value $\bar{\eta }> 0$) indicates that $\bar{\varvec{\theta }}$ is close to a stationary point. Since the functions $\varPsi ^k$ are scaled differently across the hierarchy, we suggest to use a relative stopping criterion,

$$\begin{aligned} \rho ^k_\varDelta := \frac{\varDelta ^k_\le - \varDelta ^k_>}{\varDelta ^k_\le + \varDelta ^k_>} = \frac{\varPsi ^k(\bar{\varvec{\theta }}) - \varPsi ^k(\varvec{\theta }^+)}{\varDelta ^k_\le + \varDelta ^k_>} \le \eta \end{aligned}$$

(20)

for a user-specified value of $\eta$. Due to Lemma 1 the denominator monotonically increases with k, hence the criterion becomes looser for larger k.

Contribution: The novel stopping criterion we derived (Eq. 20) allows to speed up particularly the early stages of graduated optimization. Interestingly, there is a connection between the above stopping criterion and the gain ratio

$$\begin{aligned} \rho ^k_\varPsi := \frac{\varPsi ^{k-1}(\bar{\varvec{\theta }})-\varPsi ^{k-1}(\varvec{\theta }^+)}{\varPsi ^{k}(\bar{\varvec{\theta }})-\varPsi ^{k}(\varvec{\theta }^+)}, \end{aligned}$$

(21)

that is commonly used in trust region methods (e.g. [25]) to evaluate the quality of a surrogate model (here $\varPsi ^k$) w.r.t. a target cost $(\varPsi ^{k-1})$:

Lemma 2

Let $\eta \in (0,1)$. If $\rho ^k_\varPsi \ge \frac{\eta +1}{2\eta } > 0$ or $\rho ^k_\varPsi \le \frac{\eta -1}{2\eta } < 0$ then $\rho ^k_\varDelta \le \eta$.

The lemma asserts that if $\varPsi ^{k-1}$ either increases or decreases sufficiently faster than $\varPsi ^k$, then we are near a stationary points of $\varPsi ^k$ (according to the stopping criterion Eq. 20). It is less relevant in practice, but tells us that $\varPsi ^k$ and $\varPsi ^{k-1}$ (or $\varPsi ^\ell$ for any $\ell < k$) cannot behave too different when far from a local minimum. The proof uses Lemma 1 and is given in [27].

7 Numerical Results

In this section we compare the performance of the different approaches for robust cost optimization, and we are mostly interested in the quality (i.e. achieved objective value) that is reached after a sensible amount of run-time.

Implementation Remarks: The core of our implementations is a sparse but direct Cholesky solver from the SuiteSparse libraries [6]. We apply Levenberg-type damping $\mathtt {J}^\top \mathtt {J}+ \lambda \mathtt {I}$ to (i) ensure the system matrix is sufficiently positive definite for a direct solver and (ii) to obtain a dampled Newton/Gauss-Newton method for non-linear problems. The damping parameter is adjusted using the classical $\times 10$/$\div 10$ rule. In the graduated optimization method we used 6 scale levels (i.e. $k_{\max }=5$), where the scale parameter is doubled at each level. The r.h.s. $\eta$ in the stopping criterion Eq. 20 is set to $\eta =1/5$. In the figures we abbreviate lifted Gauss-Newton and lifted Newton by l-G-N and l-Newton, respectively. GOM refers to graduated optimization with an uniform allocation of iterations at each level, and GOM+ leverages Eq. 20 as stopping criterion. We use IRLS as direct method inside GOM. We allow 100 iterations (i.e. 100 times solving the underlying system equation for the update $\varDelta \varvec{\theta }$) for each method, which results in rather similar wall-clock runtimes for all methods.

7.1 Synthetic Data: Robust Mean and Image Smoothing

Estimating the mode (i.e. robust mean) of data points is arguably the simplest robust optimization problem. We follow [26] and create Gaussian distributed inliers and uniformly distributed outliers in a $[-20,20]^D$ domain. The mean of the Gaussian inlier distribution is also uniformly sampled from the same domain, hence in most cases the outliers will not be symmetrically distributed around the inlier points. Let $(\mathbf {y}_1,\cdots ,\mathbf {y}_N)$ be the entire set of data points, then the task is to estimate $\varvec{\theta }^* = \arg \min _{\varvec{\theta }} \varPsi ^{\text {mean}}(\varvec{\theta }) = \arg \min _{\varvec{\theta }} \sum _i \psi (||\varvec{\theta }- \mathbf {y}_i||)$, where our choice of $\psi$ is the Welsch kernel, $\psi (r) = \tfrac{1}{2} (1 - e^{-r^2})$. The initial value $\varvec{\theta }^0$ provided to the optimization methods is uniformly sampled as well. We depict in Fig. 2 the average objective values (and corresponding standard deviation using 100 runs) reached by several methods for different choices of inlier ratios and $D=3$. The included methods are standard IRLS, the accelerated graduated optimization method (GOM+), the lifted Gauss-Newton and Newton methods parametrizing either $w(u)=u^2$ (l-G-N$^a$, l-Newton$^a$) or $w(u) = \mathrm {sigmoid}(u)$ (l-G-N$^b$, l-Newton$^b$). Graduated optimization (GOM+) is a clear winner, and the lifted Newton method dominates the corresponding lifted Gauss-Newton version. Using the sigmoid parametrization is clearly beneficial, and we will use this parametrization from now on in the lifting-based methods.

Fig. 2.

Final objective values for robust mean instances at varying inlier ratios.

Table 1. Final objective values for the weak membrane energy.

Since $\varvec{\theta }$ has very small dimension in the robust mean example, these types of low-parametric robust estimation problems are easily solved by random sampling methods such as RANSAC and variants (e.g. [10, 22]). Therefore we now consider a problem with a high dimensional vector of unknowns. We selected the weak membrane energy for image smoothing (e.g. [5]), which is a prototypical instance of a difficult low-level image processing problem. Given an observed image $\mathbf {u}$ the weak membrane energy is given by $\varPsi ^{\text {Membrane}}(\varvec{\theta }; \mathbf {u}) = \sum \nolimits _{i \in \mathcal V} \psi ^{\mathrm {data}}(\theta _i - u_i) + \sum \nolimits _{(i,j) \in \mathcal{E}} \psi ^{\mathrm {smooth}}(\theta _i - \theta _j)$. The node set $\mathcal V$ corresponds to pixels, and the edge set $\mathcal E$ is induced by the 4-neighborhood. $\psi ^{\mathrm {data}}$ and $\psi ^{\mathrm {smooth}}$ are based on the smooth truncated kernel (see [27]). Table 1 lists the reached average objectives (and standard deviation over 25 runs) for the different methods for the $256\times 256$ “Lena” image. The initial guesses $\varvec{\theta }^0$ are uniformly sampled images from $[0,1]^{|\mathcal{V}|}$. Only IRLS falls clearly behind in terms of reported optimal value. More interesting is the evolution of objective values shown in Fig. 3, that allows to make two observations: the lifted Gauss-Newton method is the fastest to achieve a near optimal value, and the stopping criterion leveraged in GOM+ significantly accelerates convergence of graduated optimization. Further (also visual) results are provided in [27].

Fig. 3.

Evolution of $\varPsi ^{\text {Membrane}}$ w.r.t. the number of iterations. For the lifting based methods we plot the original cost $\varPsi$ and lifted one $\tilde{\varPsi }$ (Eq. 7).

Fig. 4.

Objective values (normalized w.r.t. the number of image measurements) reached by the different methods for linearized BA.

7.2 Real Data: Robust Bundle Adjustment

One of the main applications of robust cost minimization in computer vision is bundle adjustment (BA). We took 10 problem instances (the list is provided in [27]) from the “bundle adjustment in the large collection” [2]. The robust bundle objective is given by

$$\begin{aligned} \varPsi ^{\text {BA}}(\{\mathtt {R}_i\}, \{ \mathbf {t}_i\}, \{ \mathbf {X}_j\}) := \sum \nolimits _{i,j} \psi \big (|| \pi (\mathtt {R}_i \mathbf {X}_j + \mathbf {t}_i) - \mathbf {q}_{ij}|| \big ), \end{aligned}$$

(22)

where $\mathbf {q}_{ij} \in \mathbb {R}^2$ is the observed image observation of the j-th 3D point $\mathbf {X}_j \in \mathbb {R}^3$ point in the i-th image (which has associated parameters $\mathtt {R}_i \in SO(3)$ and $\mathbf {t}_i \in \mathbb {R}^3$). $\pi (X) = X/X_3$ is the projection function of a pinhole camera model. $\mathbf {q}_{ij}$ is measured on the image plane, i.e. the original pixel coordinates are premultiplied by the (provided) inverse calibration matrix. $\psi$ is chosen to be the smooth truncated kernel with parameter , i.e. $\psi (r) = \frac{1}{16} \left( 1-[1-4r^2]_+^2 \right)$. This choice makes the problem instances sufficiently difficult, as the initial inlier ratio of image observations ranges between 14% and 50% (depending on the dataset). The inlier ratios obtained after robust cost minimization cluster around 60% for the best obtained local minima.

Fig. 5.

Evolution of $\varPsi ^{\text {BA}}$ w.r.t. the number of iterations for the Venice-427 instance.

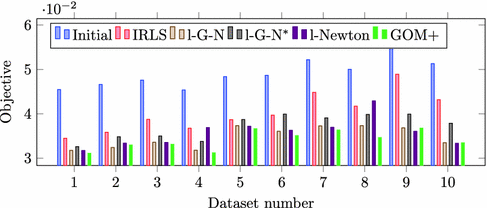
First, we focus on a linearized version of bundle adjustment, where the residuals $\mathbf {f}_{ij} = \pi (\mathtt {R}_i \mathbf {X}_j + \mathbf {t}_i) - \mathbf {q}_{ij}$ are replaced by their linearized versions w.r.t. the provided initial values. The non-robust objective is therefore convex, and the performance differences depicted in Fig. 4 indicate how well each method escapes poor local minima. In order to obtain similar objective values regardless of the dataset size, the objective values are normalized w.r.t. the number of image measurements. The unnormalized BA objective values Eq. 22 are approximately between 6000 and 60000 (depending on the dataset and method). Thus, none of the methods is in its respective comfort zone. IRLS is clearly inferior to the other methods, and GOM+ is slightly ahead of the lifted formulations. l-G-N$^*$ is the lifted Gauss-Newton method, but the lifted parameters $u_i$ are initialized to their optimal value (given the initial values $\varvec{\theta }^0$). The resulting performance is between IRLS and l-G-N. If we take a closer look on the evolution of objectives (Fig. 5), then the lifted Gauss-Newton method reduces the actual cost $\varPsi ^{\text {BA}}$ very quickly, although graduated optimization eventually reaches a better minimum.

Fig. 6.

Objective values (normalized w.r.t. the number of image measurements) reached by the different methods for metric BA.

Figure 6 illustrates the reached objectives (normalized w.r.t. the number of image measurements) by the different methods for non-linear metric bundle adjustment. Due to the additional non-linearity introduced by the non-robust objective, the results are more diverse than the ones in Fig. 4. In particular, the lifted Newton method shows an unstable behavior. Details and results for dense disparity estimation are provided in [27].

8 Conclusion and Future Work

In this work we first unified several direct and lifting-based methods for robust cost minimization. We also demonstrated that a graduated optimization method has very competitive performance in terms of the reached objective values and in terms of speed of convergence. Hence, our recommendation is as follows: a lifted Gauss-Newton method is a very strong candidate when very fast decrease of objectives is desired, and the proposed graduated optimization approach is the method of choice when reaching the best objective is the main interest—especially when the quality of the initial solution is unknown.

The fact that the best performing methods “forget” to a large extend the given initial solution is not very satisfactory. Future work will investigate whether methods adapting to the quality of the provided starting point result in faster overall convergence.