Abstract
Predicting student’s successful completion of academic programs and the features that influence their performance can have a significant effect on improving students’ completion, and graduation rates and reduce attrition rates. Therefore, identifying students are at risk, and the courses where improvements in content, delivery mode, pedagogy, and assessment activities can improve students’ learning experience and completion rates. In this work, we have developed a prediction and explanatory model using adaptive neuro-fuzzy inference system (ANFIS) methodology to predict the grade point average (GPA), at graduation time, of students enrolled in the information technology program at Ajman University. The approach adopted uses students’ grades in introductory and fundamental IT courses and high school grade point average (HSGPA) as predictors. Sensitivity analysis was performed on the model to quantify the relative significance of each predictor in explaining variations in graduation GPA. Our findings indicate HSGPA is the most influential factor in predicting graduation GPA, with data structures, operating systems, and software engineering coming closely in second place. On the explanatory side, we have found that discrete mathematics was the most influential course causing variations in graduation GPA, followed by software engineering, information security, and HSGPA. When we ran the model on the testing data, 77% of the predicted values fell within one root mean square error (0.29) of the actual GPA, which has a maximum of four. We have also shown that the ANFIS approach has better predictive accuracy than commonly used techniques such as multilinear regression. We recommend that IT programs at other institutions conduct comparable studies and shed some light on our findings.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
The National Center for Education Statistics of the United States (2019) shows that students need about six years to graduate in academic institutions awarding a 4-year bachelor’s degree. In institutions with flexible admission policy, the same statistics indicate that only 31% of students completed graduation requirements after six years compared to 87% for institutions with a more selective admission policy. Therefore, to increase the number of students graduating in a timely manner, it is important to identify under-performing students who may fail to meet graduation requirements.
Developing data-driven decision models and applications can support academic advisors’ efforts in providing a focused supervision and raise graduation rates. To achieve this aim, researchers have proposed many different categories of attributes as predictors of students’ academic achievements (Zollanvari et al., 2017). These features can be grouped into three areas: (1) traditional factors affecting academic performance that include standardized test scores and high school grade point average (HSGPA) (Dent & Koenka, 2016; Furnham et al., 2003); (2) student demographic features such as age, gender, and socioeconomic factors that contribute to student success (Voyer & Voyer, 2014); and (3) psychological factors that include personality, self-discipline, and motivation (Richardson et al., 2012).
Early identification of struggling students can substantially improve completion, and graduation rates and reduce attrition rates. It is difficult for advisors to allocate sufficient time for each student to identify those who are struggling academically and provide proper academic guidance based on informed judgment; however, predictive modelling using machine learning algorithms can provide institutions and educators with indicators of student performance levels based on their performance in introductory and fundamental courses in the curriculum. Evans & Simkin (1989) investigated predicting students’ computer competency to learn computing skills and concepts. The main objective was to find and motivate prospective computer information systems students to advance their knowledge and skills further to enhance their employability. They also stated other objectives for their work: selecting suitable candidate for computing programs, student advising, finding competent programmers, detecting those who need extra supervision, improving course delivery, measuring predictors’ importance, and understanding the association between programming skills and other mental processes.
Machine learning and data mining techniques have enabled academics to analyze educational data and extract useful information that can assist academic advisors in comprehending students’ learning processes and advance their knowledge and skills. Classification is an essential data-mining technique that is widely used for prediction purposes. Classification algorithms learn patterns from a set of observations presented to the algorithm during the training phase. Once the learning algorithm converges to an acceptable accuracy, it can assign classes to unlabeled instances. The majority of classification techniques use supervised learning where the features of the different classes present in the data are learnt; this allows the algorithm to assign a class label to unidentified future observations. There are many methods that are used for classification: logistic regression, multilinear regression, naïve Bayes, stochastic gradient descent, k-nearest neighbors, classification trees, regression trees, random forest, support vector machine, neural networks, and deep learning.
This work aims to build a model using an adaptive neuro-fuzzy inference system (ANFIS) that predicts a student’s graduation grade point average (GPA) as an indicator of the student’s success. Students’ grades in core (introductory and fundamental) computing courses of a 4-year information technology (IT) program and HSGPA were used as predictors; the courses chosen are prerequisites for the more advanced in the program. The objective of the model was two-fold: first, to identify students who are struggling in core courses that may benefit from additional guidance. Second, to identify the most critical courses in explaining variations in students’ graduation GPA so that the program can review course content, delivery, learning resources, and assessment activities to improve student performance in these courses. ANFIS methodology has achieved better predictive accuracy than other techniques because of its hybrid architecture, which combines the learning abilities of a neural network and the reasoning capabilities of fuzzy logic to increase predictive power (Jang, 1993). Thus, ANFIS modelling is more systematic and less dependent on prior knowledge of the functional relationship between the dependent variable and its predictors (Jang, 1993). An attempt was made in this work to use ANFIS and to compare results with other methodologies, such as multiple linear regression (MLR) and particle swarm optimization (PSO) (Eberhart & Kennedy, 1995).
The remainder of this paper is structured as follows: Section two presents a review of related literature, Section three describes the adopted research methodology. The results, discussion, and limitations are presented in Sect. 4, and Sect. 5 presents the conclusions.
2 Related work
Research in educational data mining (EDM) has been conducted with three main objectives: (1) developing, or evaluating algorithms that predict student performance, (2) determining the features used to make predictions, and (3) quantify aspects of student performance at the, course, or program level. Hellas et al., (2018) analyzed 589 articles published in this area since 2010 and classified the features used into a number of categories, namely: family background; demographic information; working environment; educational background; major or course data; student incentives; and psychological, affective, and learning scales. They reported that the prediction methods used included supervised and unsupervised learning, discovering frequent patterns, feature extraction, and statistical algorithms such as correlation, regression, and t-testing. Overall, they found that GPA is the preferred summative performance metric for measuring student success at the program level. However, researchers have also used other metrics, such as student retention and dropout rates. Related research conducted in field of EDM is presented in the paragraphs below.
Do & Chen (2013) presented a neuro-fuzzy method for categorizing students into different groups (good, average, and poor) on academic performance and other socioeconomic factors. In particular, the inputs to the model were university entrance examination scores (three subjects), the overall average grade of high-school graduation examination, time until university admission after high-school graduation, student’s school location, whether private or public school attended, and student’s gender. They reported that a comparison of the model’s results with those obtained from traditional approaches that include support vector machine, naive Bayes, neural networks, and decision trees, indicated that the neuro-fuzzy method performed better than the others. In a subsequent study (Chen & Do, 2014), they refined their model by proposing a “hierarchical adaptive neuro-fuzzy inference system” (HANFIS) with an embedded Cuckoo search algorithm to manage the curse-of-dimensionality problem. The Cuckoo algorithm was used to build the rule base by optimizing the clustering parameters. The role ANFIS was to optimize the parameters of the antecedent and consequent parts of each sub-model. They reported that their model performed better in terms of accuracy, reliability was accurate, reliable, and performed better than artificial neural networks, HANFIS, and GA-HANFIS (the combination of genetic algorithm and HANFIS) models. They suggested that their work can support student admission procedures and strengthen educational institutions’ services.
Al Hammadi and Milne (2004) developed a neuro-fuzzy classification algorithm to predict student success in an engineering college. The primary function of the classifier is to discover the rules that explain students’ achievement and group them into three non-overlapping categories based on anticipated performance. They indicated that their work could support admission filtering procedures by assessing and predicting student academic ability before being accepted as well as assessing the appropriateness of entry examinations. They reported that not all entry examinations were found to be good predictors of applicants’ academic attributes and expected future performance.
Liao et al., (2019) investigated the predictive power of different data sources, the effect of combining multiple data sources on prediction performance, and whether course context matters. Cross-term predictions where generated using logistic regression and “prerequisite course grades”, “clicker correctness”, “assignment grades”, and “online quiz grades” as input into the model. They found that “prerequisite course grades” is the most significant feature in predicting student achievement, followed by “clicker data”, “assignments”, and “online quizzes” in that order. They also found that very often adding assignments and quizzes as predictors does not always enhance the accuracy of the model further in the presence of prerequisite and clicker data. They reported that, in general, their findings were consistent across five different computing courses, that include a combination of lower and upper level courses collected from two institutions. Their conclusion is that instructors should examine “prerequisite course grades” and “clicker questions” in order to identify under-performing students.
Liao et al., (2019) proposed a modelling methodology based on a support vector machine binary classifier. They used clicker data gathered for instructors when using peer instructor pedagogy to predict students’ final examination grades in the third week of the term; the model was trained on one term’s course data to predict outcomes in the following term. The model was applied to five different computing courses taught by three instructors at another two institutions and achieved comparable levels of accuracy with other methods. However, they reported that the strength of their model is that it requires only a “light source” of student data, allowing for the early identification of low-performing students. They demonstrated that their methodology could effectively predict students’ performance over various semesters of the same course at different institutions, run by other instructors, and covering the computer science curriculum.
Ahadi et al., (2015) explored different algorithms for identifying under-performing students. The objective is to allow instructors to target their efforts towards under-performing students early on and set more thought-provoking and motivating academic activities for high-performing students. In addition, students who passed an introductory programming course with minimal grades can be supervised more carefully in subsequent courses. They reported that applying machine learning algorithms to snapshots of source code data from programming assignments can identify under-performing students to a high accuracy, even if taken after the first week of the course. They experimented with nine classifiers chosen from Bayesian, rule-based, and decision tree-based family of classifiers. Two different validation processes were used: (1) a k-fold cross-validation where k is 10 and, (2) per centage split with two-thirds of the dataset used for training and cross-validating the model and the remaining third for model evaluation. Their findings indicated that, overall, decision trees performed better in terms of accuracy than the other two families of classifiers. Within the decision trees family, the random forest performed best with 86%, 90%, and 90% accuracy for predicting the “Exam question”, “Final grade”, and the mixture of both.
Pérez et al., (2018) investigated the critical factors of undergraduate student non-completion rates in a system engineering program of a private Columbian university and the data mining technique most appropriate for identifying these key factors. To achieve this, they modelled student dropout using data from 762 students collected from educational databases between 2004 and 2010 for the first, second, third, and final semester after admission. The data collected covered admission demographic information: gender, birth date, and marital status; graduation data: graduation date, the academic program, academic records that included the courses taken and corresponding scores, and the cumulative GPA. They experimented with a number of data mining algorithms that included decision trees, logistic regression, naive Bayes, and random forests. Evaluation of the selected models in terms of receiver operating characteristic (ROC) curve analysis showed that the level of performance in systems engineering courses correlates with physics and mathematics grades. The area under the curve (AUC) value indicated that the Random Forest technique produced the most accurate results. They reported that the value of AUC increased from 0.91 for the third semester to 0.97 for the last semester. The authors found four features necessary for this accuracy: the number of semesters since student enrollment, the average grade in systems engineering courses, the number of times a student fails a system engineering course, and GPA. They concluded that courses related to systems engineering had the most significant impact on dropout prediction.
Araque et al., (2009) studied the key variables that appeared to be behind students dropping out in different degree programs. The study covered three degree-awarding programs with 10,844 students from the software engineering faculty, 19 degree-program with 39,241 students from Humanities faculty, and five degree-awarding programs with 25,745 students from the Economics Sciences faculty. They developed personalized models for each degree program to compute the risk of a student dropping out and analyzed the profile for undergraduates who dropped out of their degree programs. They built a logistic regression model for each faculty based on data from 1992 onwards. Their results indicate specific variables that repeatedly have significant importance in explaining dropout rates in the three faculties. These variables are enrollment age, parents’ academic background, academic performance, psychological profile, persistence, GPA, degree type, and admission form, and course failures count in some cases. They also reported that students with low academic performance are at a high risk of dropout are those with no sound educational strategies and lack the will to achieve their objectives in life. They also found that the profile of students who tended to dropout depended on the subject studied. Therefore, they proposed a generic method based on a data warehouse approach that stores the standard data provided by students when enrolled in a program and their grades while they are registered in that program. They suggested that a software system capable of cleaning, transforming, and processing the data can determine the probability of dropout for each student and summarize his academic record. The institution can then provide appropriate supervision to any high-risk student identified to reduce attrition rates.
In a case study, Dekker et al., (2009) used a group of machine learning methods to identify students at risk, those who may be successful but require extra guidance or specific individual attention to complete the Electrical Engineering program successfully at Eindhoven University. They used features obtained from student pre-university academic records and first-semester grades. Decision trees generated results with an accuracy ranging from 75 to 80% indicating that simple and intuitive classifiers can provide useful results. Their findings also revealed that linear algebra was the strongest predictor of a student completing the program or not which was not considered as a critical course.
Hutt et al., (2018) applied a random forest methodology to successfully predict a 4-year completion period for 71.4% of the students using data from 41,359 applicants’ records. The dataset consisted of 166 attributes representing socio-demographic attributes, completion rates, academic performance, standardized test scores, participation in extramural events, work experiences, instructor ratings, and high-school supervision. They also used a probabilistic hill-climbing features selection procedure to maintain the prediction accuracy achieved, but with a reduced set of 37 features; these features evenly cover socio-demographic, cognitive, and non-cognitive attributes. They concluded that completing a college degree on time does not simply depends on a student’s situation, such as previous achievements, and experiences; instead, academic performance is significantly influenced by what students learn and practice in a college setting. However, their model has no explanatory power for the relative importance of the features used in the predictions.
Hirokawa (2018) assessed the role of “behavioral, demographic, academic background, and parent participation” features in predicting student academic performance using feature selection with support vector machine predictor. The model produced an accuracy of 81% with an F-measure of 66%. Using all likely groupings of the four features, he reported that all single, pair, and triple combinations of features, that includes behavioral characteristics, achieved an accuracy of almost 80%. His conclusions were that the behavioral attribute is a crucial attribute in predicting academic achievement, giving an accuracy of 79.22% and an F-measure of 60.22% when used on its own. The demographic attribute ranked second in significance with an accuracy of 62.5% and an F-measure of 30% when used as a single predictor. The parent attribute was shown to be the least important, with an accuracy of 31.78% when used as a single input predictor.
Cortez & Silva (2008) analyzed data from two secondary schools in Portugal. The purpose was to predict students’ grades in two secondary school core courses; namely, mathematics and Portuguese, by using past school grades (first and second periods), demographic, social, and other school-related data. The data were run on four data mining techniques: decision trees, random forests, neural networks, and support vector machines. They experimented with different input selections, including or excluding past grades as an example, and reported high predictive accuracy can be achieved provided that school grades are known for at least one previous period. The predictive models have shown that in some cases there are other pertinent features, such as those related to school: frequency of absenteeism, purpose behind school choice, and extra school educational support; demographic; and social attributes that can influence student performance in these two subjects. They proposed that more research is required to understand why and how some of these attributes affect student performance.
Koutina & Kermanidis (2011) experimented with number of machine learning algorithms to determine the most accurate algorithm for predicting the final grade of postgraduate students in an informatics program at Ionian University. They selected five courses in addition to demographic, in-term, and in-class behavioral predictors. They showed that naïve Bayes and 1-nearest neighbor produced the most accurate prediction results. They also investigated the influence of these attributes as predictors of final grade. Their conclusions were that the most important features influencing final grade were the presence in class and possession of a bachelor’s degree in Informatics; they also showed that students’ professional experience and having a second master’s degree do not contribute to the algorithm’s accuracy.
Wei & Burrows (2016) investigated the relationship between a series of computer programming courses and the impact of an introductory programming class on subsequent advanced programming courses for 195 students over an eight-semester period using correlation. Their analyses indicated that in a series of programming courses, student performance in the introductory programming class can predict their level of achievement in a data structure course, but not to the same degree of accuracy as in the advanced level programming course.
Okubo et al., (2017) predicted students’ final grades using a recurrent neural network. They used data of 108 student relating to academic activities performed through a learning management system. The model achieved 93% accuracy data from the first six weeks. They also stated that the predictions obtained from the recurrent neural network-model outperformed those obtained from a multilinear regression algorithm which achieved an accuracy of 63% in predicting the final grades based on the same data.
Amazona & Hernandez (2019) used data from an information systems program gathered over a six-semester period to predict students’ academic performance. The experimented with three methodologies, namely; naïve Bayes, decision trees, and deep learning neural networks. Their findings indicated the deep learning network performed better than the other two methods, with a 95% prediction accuracy; however, decision trees had a better recall performance metric.
Sekeroglu et al., (2019) used two datasets to evaluate the performance of five machine learning algorithms to predict and classify student performance. In particular, they used back-propagation (BP), support vector regression (SVR), and long short-term memory (LSTM) for prediction and BP, support vector machine (SVM), and gradient boosting classifier (GBC) for classification. They observed that SVR performed the best (R2 = 0.827) in prediction, while BP was the best classifier of student performance (87.7%), even though it performed worst in prediction (R2 = 0.708). They concluded that machine learning algorithms are appropriate for predicting or classifying educational data. They also indicated that by considering a variety of feature selection techniques, preprocessing raw data, and machine learning algorithms, the results could be improved.
Boetticher et al., (2005) built a model using genetic algorithms to predict students’ grades in a data structures course at beginning of the semester. Their primary aim was to provide faculty with a tool that can be used to identify students who lack adequate preparation for the course; this can help faculty direct their efforts and dedicate more attention to such students or advise them to take a suitable foundation course. They designed a preassessment examination where they grouped the questions into knowledge areas essential to successfully completing this course. The examination results were fed as input into the model to predict student expected performance. They stated that 79 per cent of students who lack satisfactory background for such a course were identified. They also used the results to identify areas in the data structure course, where a review of relevant background concepts can improve performance. The model was also used to identify students who may need registering in one or more foundation courses, changing study behaviors, or may even transfer to another major.
Pardo et al. (2016) designed a model using “recursive partitioning” algorithm to assist instructors in identifying groups of students who may need certain consideration or arrangements. Their primary aim was to provide instructors with a data-driven pedagogical interventions and tailored feedback for different student groups. They showed that the model was capable of categorizing students according to their predicted exam grades in the midterm and the final examination based on quantitative measurements derived from students’ online activities. The model was applied to a large number of students of a first-year course. They reported that the error in predicting exam grades based on a root mean square error (RMSE) criterion ranges from 15% to 20 per cent for the midterm. However, the model’s performance improved when final exam grades were used with a RMSE of less than 14.2 per cent.
Chaudhury et al., (2016) examined student success using a combination of various preprocessing techniques and machine learning algorithms. They developed a group of classifiers based on: support vector machine (SVM), decision tree C4.5, and naïve Bayes techniques using a UCI dataset with 33 attributes and 678 instances. Preprocessing was performed on the data using discretization, class balancing, and the elimination of spurious entries. The RMSE and operating characteristics curve (ROC) were used to measure the performance of the three classifiers. The authors characterized students into four nonoverlapping class types based on student success level, with the first class representing low-performing students. Their results showed that no single classifier outclassed the other two, with SVM having slightly better performance than the others when class balancing was carried out using oversampling; with under balancing, the performance of naïve Bayes improved and out-performed the others. Their results also showed that without preprocessing, the SVM classifier had a low true positive rate of 43% for low-performing students; but this rate improved significantly to 94.8 per cent with data preprocessing. The corresponding true positive rates for the other two classifiers were 93.8 per cent and 89.6 per cent for the naïve Bayes and C4.5 decision tree classifiers, respectively.
Rustia et al., (2018) built a classification model to detect students who will probably fail the “Licensure Examination for Teachers” and help them improve their performance and preparedness to reduce the dropout rate. They experimented with neural networks, support vector machines, C4.5 decision trees, naïve Bayes, and logistic regression to build their model. The dataset used was constructed from 446 student academic records that underwent the licensure examination. Initially, they identified ten features as the predictive variables. Subsequently, they used genetic programming to optimally select performance in “English, science, theories and concepts, methods and strategies, special topics, and core subjects” as the relevant predictive variables. The attributes represent the weighted average performance of students in each of the five subject areas selected, with the class label being a pass or fail. Their results showed that C4.5 Decision Tree is the best classifier for their model with an accuracy of 73.1% for identifying students who are expected to fail the “Licensure Examination for Teachers.”
Manrique et al., (2019) built dropout prediction models for students. For this purpose, they created three different feature sets and implemented four different classification algorithms. They constructed three datasets based on different feature sets: (a) global feature-based representation for any degree program, (b) local feature-based representation for specific degree programs, and (c) student data as a multivariate time-series. They constructed the datasets using academic records excluding demographic data of 2,175 students at a Brazilian university registered in two different degree programs. They implemented four traditional binary classifiers: naïve Bayes, support vector machine, random forest, and gradient boosting tree. They concluded that the local feature-based dataset produced better dropout predictions than the other two datasets; dropout can be predicted accurately using grades of a few fundamental courses without having to use sophisticated feature extraction process. They also showed that involving the temporal aspects of the data increases the computational cost as the model complexity increases; but does not seem to improve the model’s prediction accuracy. They also found that naive Bayes is the least suitable of all the approaches because the strong independence assumption does not apply to the global-based feature set. The best results were obtained using the random forest and gradient boosting tree ensemble models.
Lagman et al., (2019) explored the use of the Naïve Bayes algorithm to build a classifier that predicts and identifies students who may not complete the program on time so that proper corrective actions and students’ retaining policies can be implemented by institutions in the Philippines at an early stage in the student’s program. The dataset consists of graduation status as a binary target variable with fifteen input predictors. These input predictors include: student’s gender; student’s location; financial assistance given by the school; four entrance examination results comprised of four sections: Abstract, Verbal, Numeric and Science; first year first term grades of five subjects comprising: Algebra, IT Fundamentals, Programming, English, Education Values, and Physical Education. Logistical regression techniques were employed to reduce the number of predictors to the eight most significant features. These predictors were “gender, scholarship, verbal section of entrance examination result, abstract section of entrance examination result, algebra, IT fundamentals, programming, and educational values.” The model’s accuracy rate in predicting student graduation status was reported to be 85.22%.
The literature review indicates that he main interest of researchers in EDM has been to evaluate the effectiveness of specific algorithms, techniques, and features and not to conduct further analysis that can aid evidence-based educational decision making at the course or program level. This view is supported by Papadogiannis et al., (2020) in their extensive review of EDM research when concluded that “A limited application of data mining methods has been found to support educational policy-making and institutional decision-making. We believe that the development of research aimed at their own application in the daily teaching process but also in support of decision making at the level of educational policy, should be an alternative.”
In this work, we aim to build an EDM model based on ANFIS to predict student graduation GPA. The ANFIS architecture has the ability to capture the underlying structural relationship between the input features and the performance measure without any predetermined assumptions about the form of this relationship. In addition to predicting student’s graduation GPA at an early stage in the program, the model is also used to conduct further analysis that identify the courses causing most variations in graduation GPA to aid academic administrators in taking appropriate actions to improve students’ performance as measured by their graduation GPA. Another distinguishing feature of our model is the reliance on data readily available in students’ records. In particular, it requires student HSGPA and his performance in a small set of core introductory courses that act as prerequisites to more advanced courses in the program.
3 Research methodology
ANFIS is a hybrid analytical methodology that combines the strengths of neural networks and fuzzy logic systems in its prediction mechanism. Neural networks control the representation of information and the physical architecture of the model. In comparison, fuzzy inference systems emulate human reasoning and strengthen the model’s ability to manage uncertainty within the system (Eberhart & Kennedy, 1995; Negnevitsky, 2017). ANFIS learns the features of a particular pattern through the examples presented to the system and iteratively modifies the system parameters to converge towards the system’s specified error criterion and improves the prediction. Thus, we developed an ANFIS-based GPA prediction model to avoid making any pre-assumptions that may not hold concerning the complexity, uncertainty, and linearity, or otherwise of the cause-effect relationship between the graduation GPA and its determinants. On the other hand, classical techniques such as MLR require a predetermined functional form of the causal relationship between the input predictors and output (Pal & Bharati, 2019).
Models that use fuzzy inference in its reasoning process fall into two groups, which differ primarily in representing different information types. The first group includes “linguistic models” also known as Mamdani fuzzy models. These are based on sets of if-then rules with imprecise predicates and use fuzzy reasoning (Mamdani, 1974; Dubois et al., 1997). In these models, fuzzy variables are assigned linguistic labels that are described by fuzzy membership functions; thus, a fuzzy model is essentially a qualitative representation of the underlying fundamental system (Tanaka & Sugeno, 1998). The other category of fuzzy models is based on the Takagi-Sugeno inference process (Terano et al., 1994; Filev & Yager, 1994; Sproule et al., 2002). These models have logical rules with a fuzzy premises and functional consequents. Fuzzy models based on the Takagi-Sugeno method of reasoning assimilate the capability of linguistic models for qualitative and quantitative information representation (Rutkowski, 2004).
Functionally, the basic difference between the Mamdani and the Sugeno fuzzy systems is that a Sugeno output membership functions have either linear or constant functional form. A Sugeno fuzzy inference system (FIS) performs better than a Mamdani FIS in terms of computational efficiency, predictive precision, and robustness in processing noisy input data. The adaptive techniques used to determine the parameters of the membership functions in a Sugeno system ensures the continuity of the output function and are more appropriate to quantitative analysis (Subhedar & Birajdar, 2012; Hamam & Georganas, 2012). As a result, this study uses the ANFIS methodology based on a Sugeno FIS model to predict graduation GPA. The following subsections describe the structure and learning mechanisms of the model.
3.1 Adaptive Neural-Network-Based Fuzzy Inference System
Fuzzy logic systems lack the learning capability and adaptability of neural networks; thus, their parameters must be determined and modified by an external object. On the other hand, neural networks are black boxes; they can learn from data, but their reasoning is encoded in the connection weights of their neurons’ connections (Mitra & Hayashi, 2000; Jang, 1993) has proposed an intelligent system architecture by integrating fuzzy inference systems and neural networks where the strength of each system complement the other; this intelligent system structure is a neural network that is functionally equivalent to a Sugeno fuzzy inference model called the adaptive neural-based fuzzy inference system (ANFIS). The neural network component’s task is to learn, from the input-output examples, the fuzzy rules’ membership functions’ parameters, while the inference system’s role is to generate the approximated output (Jang, 1993; Negnevitsky, 2005).
3.2 ANFIS Architecture
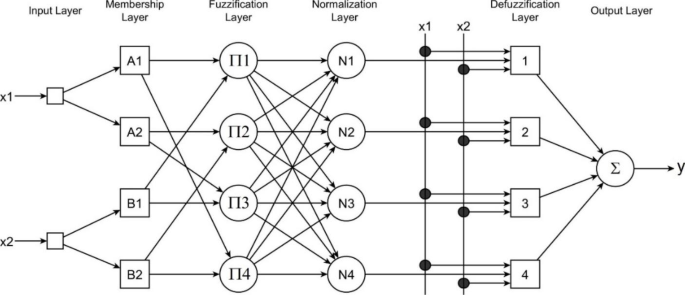
A six-layer ANFIS structure corresponding to a first-order Sugeno fuzzy model with two inputs and two membership functions per input is shown in Fig. 1 (Negnevitsky, 2005). The network has fixed and adaptive neuron types. Fixed neurons are represented as circles, and adaptive ones are depicted as squares.
The following description is based on (Negnevitsky, 2005). For a first-order Sugeno fuzzy model, the rule base is expressed as follows:
Gaussian, triangular, sigmoidal, and S-shaped, among other membership functions, can be used with an ANFIS. The Sugeno neuro-fuzzy learning mechanism provides better estimates for Gaussian membership functions. For Gaussian functions, the learning algorithm can exploit all the information imbedded in the training set to calculate each rule consequence compared with triangular membership functions (Jain, and Martin, 1998). Sambariya & Prasad (2017) found that a Gaussian membership function performs best when the range of an input’s values are covered by three of five membership functions.
Assume that the membership functions of fuzzy sets Ai and Bi for i = 1 and 2 are two Gaussian membership functions µAi and µBj, respectively. A product T-norm, a logical and operator, is used to evaluate the rules’ conditional parts which results in:
Evaluating the rule’s implication and consequents give:
Leaving the arguments out:
The above equation can be rewritten as:
where,
3.3 ANFIS Learning
With ANFIS, a least-squares error criterion and a gradient descent algorithm are used to learn the parameters of the membership functions (Jang, 1993). Initially, each neuron’s membership function is assigned an activation function such that the centers of the membership functions are set such that the widths and slopes adequate overlapping of the individual functions and equally cover the entire input range (Negnevitsky, 2005). For each epoch, training is performed in two steps: a forward pass and a backward pass. In the forward pass, each rule’s consequent parameters are estimated using a least squares algorithm. When the rule’s consequent parameters are determined, the network can compute the output error. The errors are propagated back as inputs into the backward pass, and the parameters of the membership functions are modified using the back-propagation learning algorithm (Negnevitsky, 2005). In Jang’s learning algorithm (Jang, 1993), both the antecedent and consequent parameters are optimized through the learning process. The consequent parameters are adjusted in the forward pass, while those of the antecedent remain fixed. On the other hand, the antecedent parameters are modified in the backward pass, whereas the consequent parameters remain fixed. Membership functions and their parameters can also be set by a human expert and kept fixed during the training process particularly when the input-output dataset is relatively small (Negnevitsky, 2005).
3.4 Programming Environment
The Sugeno-type neuro-fuzzy system was implemented using MATLAB functions (MathWorks, 2021a, b):
-
1.
fismat = genfis(trnDataInput, trnDataOutput, optGenfis), the genfis() function uses a fuzzy c-means clustering algorithm to extract a set of fuzzy rules the fits the data pattern to create a fuzzy inference system. The embedded function fcm( ) determine the number of rules and corresponding membership functions for the antecedents and consequents. The arguments for genfis() are described below (MathWorks, 2021a):
-
trnDataInput: a matrix in which each row contains the input values of a single observation. The matrix trnDataInput has one column per input.
-
trnDataOutput: a matrix in which each row contains the output values of a single observation. In this work, each input vector has one output, GPA, and thus, trnDataOutput is a column vector.
-
optGenfis = genfisOptions(clusteringType) creates a default option set for generating a fuzzy inference system structure using genfis(). In this study, we used subtractive clustering to identify cluster centers. Dot notation can be used to override default values, such as the number of membership functions and the input membership function type.
-
2.
The model was rebuilt using k-fold cross-validation data (k = 5) to build a fuzzy inference system. To enforce the use of validation data, the AnfisOptions function was used to set the ValidationData option:
optAnfis = anfisOptions(‘InitialFIS’,fismat, ‘ValidationData’, valData);
-
3.
fismat1 = anfis(trainingData, optAnfis), which fine-tunes a Sugeno-type fuzzy inference system, fismat, using training data and optAnfis generated by anfisOptions(). These options provide the user with the means to assume an initial FIS object to tune, validation data to prevent overfitting to training data, and training algorithm options such as EpochNumber, ErrorGoal, InitialStepSize, StepSizeDecreaseRate, StepSizeIncreaseRate, OptimizationMethod, among others (MathWorks, 2021b). The default values were used for the remaining options.
-
4.
predictedOutput = evalfis(inputData, fismat1) uses the fuzzy inference system fismat1 and test data as input data to predict the graduation GPA.
3.5 The Information Technology Program Composition and Structure
The IT program, which started in September 2010, was developed based on the ACM curriculum guidelines for information technology programs, emphasizing networking and security. The number of students registered in the program in the last three years has risen from 72 to 287, of which 65% are from 24 nationalities, mainly from Middle Eastern countries. Students are admitted to the program if they have obtained a high school certificate, scientific section, with a minimum school grade average of 70% or equivalent. The courses taught in the scientific section are information technology, mathematics, physics, biology, chemistry, Arabic, English, and Islamic studies.
The courses comprising our 4-year IT program are categorized as follows: general education, core (introductory and fundamental), advanced, and selected elective courses where the number of courses is 10, 16, 9, and 4 in each group, respectively. In addition, students have to present a design project and complete an eight-week internship experience. The core, advanced, and selected elective courses of the program are listed in Table 1.
In this work, we chose seven IT core courses, as depicted in Table 2, together with HSGPA to predict final student graduation GPA. These courses were chosen because they provide the necessary background for students to progress successfully through the advanced courses of the program. Hirokawa (2018) assessed the significance of behavioral, demographic, academic background, and parent involvement features in predicting student academic performance using a support vector machine and feature selection. He tested all possible single, pair, and triple combinations. His findings indicated that the behavioral attribute is vital in predicting student academic achievement, with the demographic characteristic being the second most important. Therefore, to account for non-academic factors, we have chosen HSGPA as a proxy for representing academic aptitude, sociodemographic, and behavioral factors.
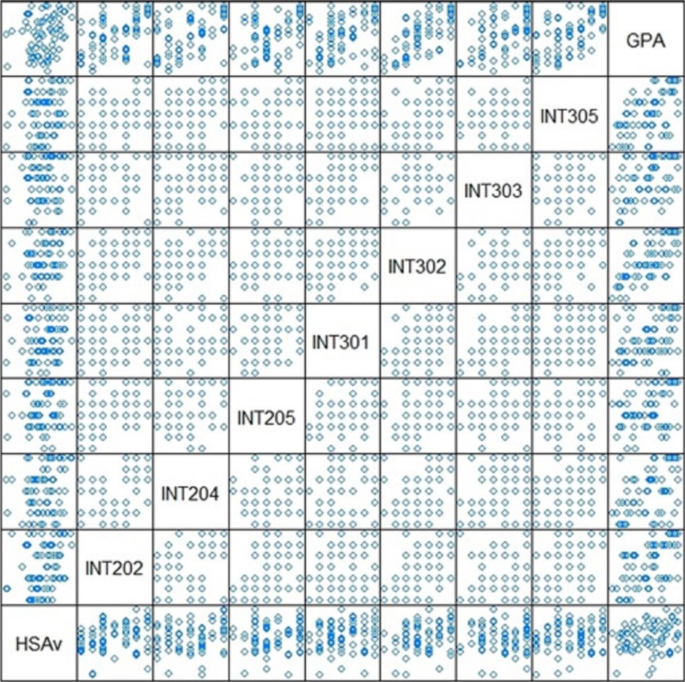
Algorithms and problem-solving, object-oriented programming, and data structures are highly correlated, and each is a prerequisite for the following course in a given order. Thus, only the data structure course was selected as a measure of programming knowledge and skills. The scatterplot matrix shown in Fig. 2 indicates that there is no significant correlation between any two predictors.
Student GPA is calculated according to the formulae:
Where,
α: Course credit hours, α = 3 for all 41 IT program courses.
Gi
grade point score of course i, i = 1, …, 41; see Table 3.
Total credit hours
123 for the IT Program.
3.6 Datasets
The IT dataset was prepared from transcripts of 100 students who had graduated from the program with a bachelor’s degree in IT since August 2014 and their admission HSGPA. Data from students who completed the program successfully were used to train, validate, and test the model. Data of students who are currently enrolled or dropped out cannot be considered as the goal of the model is to forecast the final graduation GPA. Seventy records were allocated for training using k-fold cross-validation (k = 5), and the remaining records were used for testing.
In addition, we have also used two other datasets for comparison and evaluation purposes. The first dataset is the HSC Level Student’s GPA dataset from Kaggle, which is a publicly available dataset that contains the grades of 526 students in seven different high school subjects and their corresponding GPA on a scale of 0–5 (Kaggle, 2021). The other dataset used is for the Computer Engineering program constructed from the records of 84 students attending the same sections of the IT courses used in the study over the same period.
3.7 Predictive and Explanatory Model Performance
Predictive modelling is defined as the process of developing and applying a numerical model or a data-mining algorithm to a dataset for forecasting new or future observations. The primary aim is to predict a new observation’s output given its input values (Gkisser, 2017). On the other hand, the explanatory aspect of the model provides information about the strength of the underlying causal relationship between the input and output variables and does not imply its predictive power (Shmueli, 2010). There is no need in predictive modelling to determine the role of each input variable in the underlying causal structure as the focus is on the association rather than causality between the input variable and the dependent variable (Shmueli, 2010). A main difference between explanatory and predictive performance measurement metrics is the source of data used in their computation (Stone, 1974; Geisser, 1975). In general, metrics computed from the data on which the model was trained and built tend to be over-optimistic in terms of their prediction accuracy. Thus, the testing data subset serves as a more realistic context for evaluating a model’s predictive ability (Mosteller & Tukey, 1977). In predictive modelling, model performance is measured by metrics such as RMSE on testing data that were not used in model building. On the other hand, the explanatory power of individual input variables is assessed using metrics computed by rerunning the model on the training dataset (Stone, 1974; Geisser, 1975).
4 Results and discussion
The following subsections discuss the effectiveness of the model as a tool for predicting and explaining variations in student graduation GPA for the IT program. In addition, the results from applying the model to two other datasets were examined for consistency. The model predictions were also compared to those obtained using a simple average of the predictors, MLR, and PSO.
4.1 Model Performance
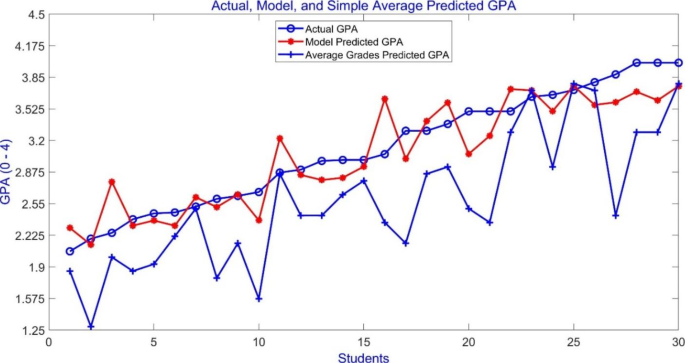
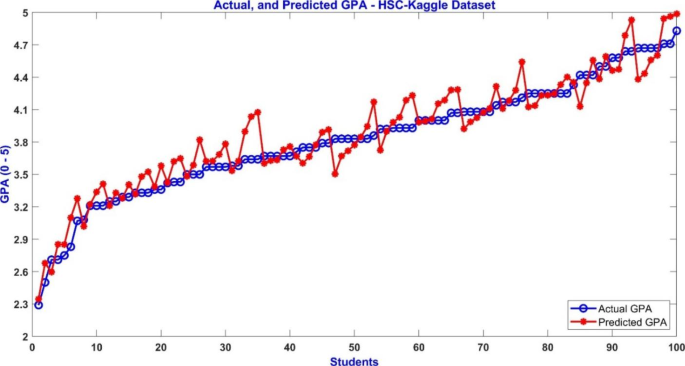
The IT dataset was divided into two disjoint subsets: training and testing with 70 and 30 records, respectively. The model was trained using k-fold cross-validation with k = 5 to reduce overfitting. The RMSE of the model predictions obtained using the test data was 0.28. The model’s prediction performance was compared to that obtained simply by computing the average grades of the courses used as predictors; the RMSE obtained using the average of core courses as a predictor was 0.650, indicating a more accurate prediction by the model. Figure 3 shows the actual GPA, model-predicted GPA, and average grade of the predictor courses for each student in the testing dataset. Figure 3 also indicates that the simple average consistently underestimates the graduation GPA.
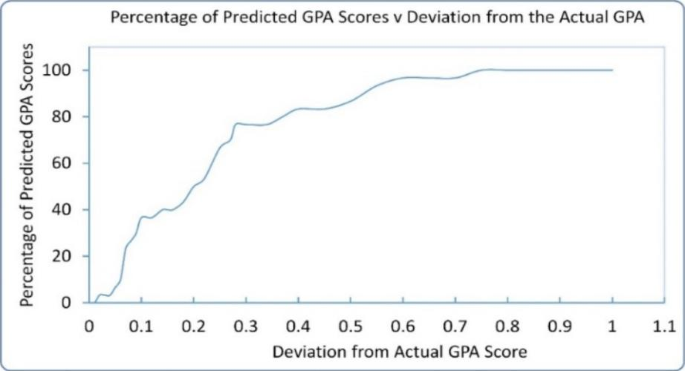
The percentage of predicted values within one RMSE (0.29) of the true respective GPA values was 77%. Figure 4 shows the percentage of GPA scores predicted with as a function of the deviations from the true GPA. It can be seen that all predictions fall within 0.75 of the real GPA. Thus, the model can provide sufficiently close estimates of the expected final GPA, giving both struggling students and advisors the opportunity to take appropriate actions and react in time so that they may be better prepared for advanced courses.
The accuracy of the predictions was also compared to those obtained from the MLR and PSO algorithms using the same IT dataset. Table 4 lists the RMSE values of the four approaches using the testing set. Table 4 indicates that the neuro-fuzzy model performed better than the other techniques to varying degrees. As explained previously in Sect. 3.3, ANFIS models can learn the underlying relationship (linear or otherwise) between the predictors and output from the data rather than assuming a predetermined relationship, as is the case with MLR and PSO, where the objective is to estimate the parameters of the relationship (Pal & Bharati, 2019).
4.2 Model Applicability
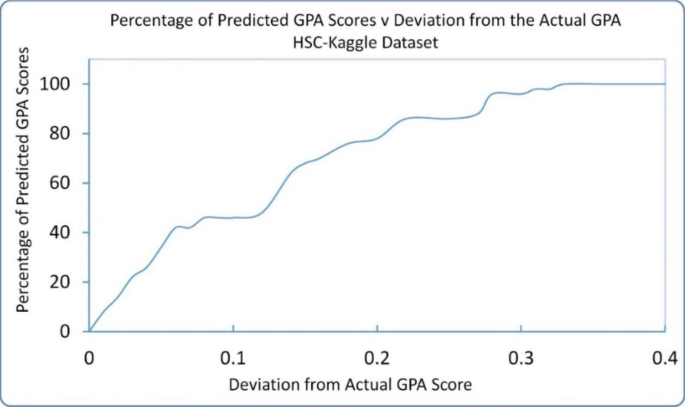
The model was also tested on the HSC Level Student’s GPA dataset from Kaggle. One hundred records were used as hold out testing data, while the remaining were used for training and model validation using k-fold (k = 5) cross-validation. The RMSE resulting from running the model on the test data was 0.15. Figure 5 displays the real GPA and model calculated GPA. Figure 6 illustrates the performance of the model in terms of the predicted GPA scores with respect to deviations from the actual GPA. The model forecasted 71% of the GPA values within one RMSE (0.15), and all GPA scores fall within 0.35 of the actual GPA. The accuracy of the model has improved considerably using the Kaggle dataset because the size of the Kaggle dataset is more than five times that of the IT dataset. The RMSE when using MLR on the HSC Kaggle dataset was 0.163, indicating that the accuracy of ANFIS was slightly better than the MLR approach even though the GPA in the HSC dataset is calculated as a linear combination of the seven grades used as predictors, making it most suitable for the MLR approach.
We also examined the behavior of the model when the same GPA predictors for the IT program were used as predictors of graduation GPA for computer engineering students at our institution. The core IT courses used in this study are part of the courses required for the CE program. However, the CE program requires the completion of 140 credit hours compared with 123 for the IT program. Moreover, the IT courses used as predictors are not prerequisites for more advanced courses in the CE curriculum. The CE dataset was constructed from the data of 84 students attending the same sections of the IT courses used in the study over the same period. When applied to the testing data, the RMSE of the model was 0.645. The conclusion drawn from these results is that programs with different curriculum designs have different sets of courses that act as predictors depending on how they influence performance in subsequent courses in the curriculum. This is where our model can be useful in identifying the courses that are most important in predicting student GPA for any program.
4.3 Predictive Importance of Input Variables
One of the common techniques for measuring the relative predictability strength of an input variable is backward elimination (Kohavi & John, 1997). Initially, the ANFIS model was trained using all input variables, and the corresponding RMSE was computed using the testing data that were held out. Next, the model was retrained by removing each input variable one at a time and examining the change in the RMSE when the model was run on the same testing data. The higher the resulting change in the RMSE due to the removal of a particular input predictor, the higher the relative predictive influence of that variable (Kohavi & John, 1997). The RMSE resulting from dropping one course at a time, as a predictor, is indicated in Fig. 7 by the value on the corresponding horizontal bar and should be compared with the RMSE value on the bottom bar (all input variables used). The difference, which represents how much the RMSE has increased as a result of dropping that course, gives an indication of the strength of that course as a predictor. Therefore, Fig. 7 shows that HSGPA is the most significant single predictor of graduation GPA. This is consistent with findings in other extensive studies that both standardized test scores and high-school GPA predict college success and that the latter is a much stronger predictor (Stumpf & Stanley, 2002; Waugh et al., 1994). It also gives credence to the conception that most high-performing students at school continue to be so at post-high school education and the idea that the best predictor of future behavior is past behavior (Hutt et al., 2018). The courses: data structures, operating systems, and software engineering come second, with the networking course being the least effective predictor. However, all input variables contributed in varying degrees to the GPA prediction. The lack of data availability for similarly designed IT programs has prevented the generalization of these findings to other programs.
4.4 Model Explanatory Performance
We performed a sensitivity analysis to determine the causal importance of each input variable. Many methods have been proposed for neural network-based sensitivity analyses (Cao et al., 2016). The partial derivative algorithm (Dimopoulos et al., 1995) and the input perturbation algorithm (Zeng & Yeung, 2003) have been shown to perform better than other algorithms (Gedeon, 1997; Wang et al., 2000). However, two major weaknesses are observed in the partial derivative technique. First, the method cannot be used to analyze neural networks with a non-differentiable activation function; second, the magnitude effect of the input variable on the output as a result of a perturbation in a given imput variable cannot be assessed properly (Cheng & Yeung, 1999).
In this work, we chose the perturbation method for the reasons cited above. This method perturbs a given input variable by adding noise while keeping all other inputs unchanged. The change ratio of the output variable with respect to perturbation in the input variable was calculated. This process was repeated for different noise levels. The input variable with the highest change ratio has the strongest explanatory effect on the output of the system being analyzed (Lamy, 1996). However, the crucial issues are: (i) selecting an appropriate index for computing the change in the output and (ii) the range of input perturbation levels. Bai et al. (2011) investigated several approaches to neural network sensitivity and showed that the formula given by Reddy et al. (2006) described in Eq. (9) measures both the direction and magnitude of the sensitivity of a neural network output with regard to a perturbation in a particular input variable value:
where,
,
Sj is a sensitivity index of the output with respect to input j,
N is the number of input training record, and \(\widehat{y}, and y\) measures the network output with and without perturbation using the training data, and
\({\widehat{u}}_{i}, and {u}_{i}\)are input variable i with and without noise, respectively.
The optimum range of the input perturbation ratio should be determined in order to accurately assess the sensitivity to perturbations in the input variables (Bai et al., 2011). The sensitivity spectra can be clipped if the perturbation is significant. Generally, results become less reliable the further a pignal; it has been found that the sensitivity measurements of input perturbation ratio are relatively stable within [-20%, 20%] variations in the input variables (Bai et al., 2011).
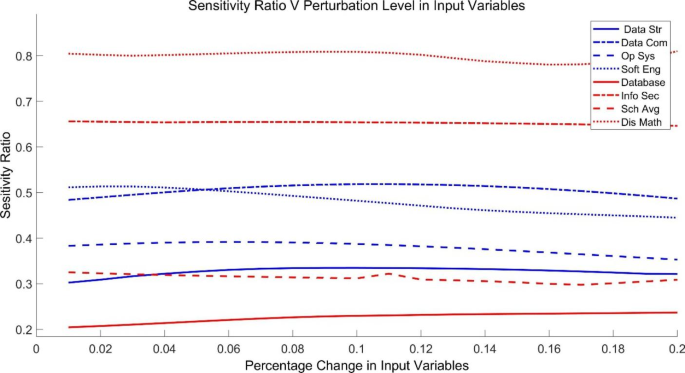
After the neuro-fuzzy model training had been completed, the sensitivity spectra values at increasing levels of input perturbation levels ranging from 0 to 20 per cent were calculated in steps of 0.01 according to formula (9), using training data. Figure 8 shows the sensitivity index of the model’s output for each input variable, which indicates that the discrete mathematics course is the most significant factor in explaining variations in graduation GPA. This is followed by software engineering and information security. The results also indicate that HSGPA have a considerable influence in explaining variations in graduation GPA Networking, and database courses seem to have less impact than other courses. The database management system course appears to have no role as an explanatory variable. Again, we hope that similar research in other institutions may shed light on whether these findings can be generalized.
4.5 Model Contribution
A review by Hellas et al., (2018) has shown that many models have been developed in the literature to predict students’ graduation success based on academic, social, economic, behavioral, and demographic attributes. However, very few attempts have been made to measure the predictive power or explain the sources of variation in students’ GPA scores so that actionable measures can be taken. A distinctive characteristic of our model is that, in addition to predicting students’ GPA and the predictive importance of these courses, it also identifies the courses that explain variations in students’ GPA so that these courses are redesigned with regard to the suitability of the content, delivery mode, pedagogy, assessment tools, and instructor domain. Another important feature of the model is its dependence on students’ grades, which are readily available, unlike other attributes that are difficult to obtain and quantify. The model can be used for any academic program to identify a set of core courses that act as predictors of student success in terms of graduation GPA. The model’s predictive performance was shown to be more accurate than that of the traditional MLR model.
4.6 Limitations and Model Validity
Although the model provides good predictive results, there are a number of issues that may adversely affect the model performance. Tomkin et al., (2018) reported that grades could be influenced by different grading standards and styles, as well as differences in the accepted grades’ distribution of instructors. Thus, a high turnout of faculty teaching courses used as predictors can have an adverse effect on the model’s predictive and explanatory power. However, all courses used as predictors in our study were taught by the same faculty over the time span covered by the dataset. Second, as a result of academic programs reviews, changes in courses’ content, teaching methodology, and assessment methods can cause deviations in grades that affect students’ GPA. In their investigation of the effects of curriculum modifications of first-year introductory computer programming courses, e Silva et al., (2003), have found that the sequence and selection of taught courses, students’ class-time load, balance of lectures, and practical sessions were some of the factors contributing to students’ academic performance. Third, GPA is viewed as measure of academic competency; as such, students tend to choose elective courses where high grades can be obtained to raise their GPA and improve their prospects of a rewarding professional career or enrollment in a graduate program. The wider the choice of elective courses in the curriculum, the higher the variation in students’ GPA as a result of students selecting diverse electives (Tomkin et al., 2018). Finally, in this work, we have used HSGPA as a substitute for attributes such as academic ability, students’ socio-economic status, behavioral characteristics, and demographic attributes. Researchers have shown that these are key features in predicting student academic performance (Hellas et al., 2018; Hirokawa, 2018); accordingly, changes in these characteristics over the program’s period may result in a biased estimate of student’s GPA if they are not explicitly included in the model as predictors.
4.7 Limitations and Model Validity
Although the model provides good predictive results, there are a number of issues that may adversely affect the model performance. Tomkin et al., (2018) reported that grades could be influenced by different grading standards and styles, as well as differences in the accepted grades’ distribution of instructors. Thus, a high turnout of faculty teaching courses used as predictors can have an adverse effect on the model’s predictive and explanatory power. However, all courses used as predictors in our study were taught by the same faculty over the time span covered by the dataset. Second, as a result of academic programs reviews, changes in courses’ content, teaching methodology, and assessment methods can cause deviations in grades that affect students’ GPA. In their investigation of the effects of curriculum modifications of first-year introductory computer programming courses, e Silva et al., (2003), have found that the sequence and selection of taught courses, students’ class-time load, balance of lectures, and practical sessions were some of the factors contributing to students’ academic performance. Third, GPA is viewed as measure of academic competency; as such, students tend to choose elective courses where high grades can be obtained to raise their GPA and improve their prospects of a rewarding professional career or enrollment in a graduate program. The wider the choice of elective courses in the curriculum, the higher the variation in students’ GPA as a result of students selecting diverse electives (Tomkin et al., 2018). Finally, in this work, we have used HSGPA as a substitute for attributes such as academic ability, students’ socio-economic status, behavioral characteristics, and demographic attributes. Researchers have shown that these are key features in predicting student academic performance (Hellas et al., 2018; Hirokawa, 2018); accordingly, changes in these characteristics over the program’s period may result in a biased estimate of student’s GPA if they are not explicitly included in the model as predictors.
5 Conclusions
In this study, we have built a prediction and explanatory model based on the ANFIS methodology to predict the final GPA of students registered in the IT program at Ajman University. The developed tool can be used for any academic program where fundamental and introductory courses affect student performance in subsequent higher-level courses. In our case, students’ grades in core IT courses and HSGPA were used as predictors. For the IT program at our institution, HSGPA has been found to be the most significant predictor of graduation GPA; the courses, data structures, operating systems, and software engineering come second, with the networking course being the least effective predictor. However, all input variables contributed in varying degrees to the predicted GPA. Sensitivity analysis was incorporated into the model to identify the relative importance of each course used as an explanatory input variable of variations in the final GPA. Our results indicate that discrete mathematics is the most influential course causing variations in GPA graduation. This is followed by software engineering, information security, and HSGPA as input variables as a source of GPA variations. In summary, our model can provide insight into which students require academic guidance and the core courses that have the strongest influence on student achievement levels so that appropriate actions can be taken to maintain a strong and successful undergraduate IT program. We have also shown that the ANFIS methodology can produce improved results compared to traditional MLR technique based on a comparative analysis of three datasets of different programs. This superior performance can be attributed to ANFIS’s capability of learning the underlying relationship (linear or otherwise) between the predictors and output from the data. The lack of access to datasets for similar IT programs at other institutions has prevented us from concluding whether our results are general in nature. It is hoped that similar IT programs at other institutions may conduct comparable studies and shed some light on our findings.
Data Availability
Two datasets that support the findings of this study are available from Ajman University but restrictions apply to the availability of these data, which were used after approval for the current study, and so are not publicly available. Data are however available from the authors upon reasonable request and with permission of Ajman University. The other dataset analyzed during the current study is available in the Kaggle repository: HSC Level Student’s GPA Dataset. This dataset was derived from the following public domain resources: https://www.kaggle.com/tahamidulislamsamin/final-training-data-project-gpa?select=test+data+rank.csv
References
Ahadi, A., Lister, R., Haapala, H., & Vihavainen, A. (2015). Exploring machine learning methods to automatically identify students in need of assistance. In Proceedings of the eleventh annual international conference on international computing education research (pp. 121–130)
Al-Hammadi, A. S., & Milne, R. H. (2004). A neuro-fuzzy classification approach to the assessment of student performance. In 2004 IEEE International Conference on Fuzzy Systems (IEEE Cat. No. 04CH37542) (Vol. 2, pp. 837–841). IEEE
Amazona, M. V., & Hernandez, A. A. (2019). Modelling student performance using data mining techniques: Inputs for academic program development. In Proceedings of the 2019 5th International Conference on Computing and Data Engineering (pp. 36–40)
Araque, F., Roldán, C., & Salguero, A. (2009). Factors influencing university drop out rates. Computers & Education, 53(3), 563–574
Bai, R., Jia, H., & Cao, P. (2011). Factor Sensitivity Analysis with Neural Network Simulation based on Perturbation System. J Comput, 6(7), 1402–1407
Boetticher, G. D., Ding, W., Moen, C., & Yue, K. B. (2005). Using a pre-assessment exam to construct an effective concept-based genetic program for predicting course success. ACM SIGCSE Bulletin, 37(1), 500–504
Cao, M., Alkayem, N. F., Pan, L., Novák, D., & Rosa, J. L. G. (2016). Advanced methods in neural networks-based sensitivity analysis with their applications in civil engineering. Artificial neural networks: models and applications, Rijeka, Croatia, IntechOpen, 335–353
Chaudhury, P., Mishra, S., Tripathy, H. K., & Kishore, B. (2016). Enhancing the capabilities of student result prediction system. In Proceedings of the Second International Conference on Information and Communication Technology for Competitive Strategies (pp. 1–6)
Chen, J. F., & Do, Q. H. (2014). A cooperative cuckoo search–hierarchical adaptive neuro-fuzzy inference system approach for predicting student academic performance. Journal of Intelligent & Fuzzy Systems, 27(5), 2551–2561
Cheng, A. Y., & Yeung, D. S. (1999). Sensitivity analysis of neocognitron. IEEE Transactions on Systems Man and Cybernetics Part C (Applications and Reviews), 29(2), 238–249
Cortez, P., & Silva, A. M. G. (2008). Using data mining to predict secondary school student performance
Dekker, G. W., Pechenizkiy, M., & Vleeshouwers, J. M. (2009). Predicting Students Drop Out: A Case Study. International Working Group on Educational Data Mining
Dent, A. L., & Koenka, A. C. (2016). The relation between self-regulated learning and academic achievement across childhood and adolescence: A meta-analysis. Educational Psychology Review, 28(3), 425–474
Dimopoulos, Y., Bourret, P., & Lek, S. (1995). Use of some sensitivity criteria for choosing networks with good generalization ability. Neural Processing Letters, 2(6), 1–4
Do, Q. H., & Chen, J. F. (2013). A neuro-fuzzy approach in the classification of students’ academic performance. Computational intelligence and neuroscience, 2013. https://doi.org/10.1155/2013/179097
Dubois, D., Prade, H., & Yager, R. R. (Eds.). (1997). Fuzzy information engineering: a guided tour of applications. John Wiley & Sons, Inc.
Eberhart, R., & Kennedy, J. (1995). A new optimizer using particle swarm theory. In MHS’95. Proceedings of the sixth international symposium on micro machine and human science (pp. 39–43). Ieee
Evans, G. E., & Simkin, M. G. (1989). What best predicts computer proficiency? Communications of the ACM, 32(11), 1322–1327
Filev, D., & Yager, R. R. (1994). Essentials of fuzzy modeling and control. Sigart Bulletin, 6(4), 22
Furnham, A., Chamorro-Premuzic, T., & McDougall, F. (2003). Personality, cognitive ability, and beliefs about intelligence as predictors of academic performance. Learning and individual Differences, 14(1), 47–64
Gedeon, T. D. (1997). Data mining of inputs: analysing magnitude and functional measures. International Journal of Neural Systems, 8(02), 209–218
Geisser, S. (1975). The predictive sample reuse method with applications. Journal of the American statistical Association, 70(350), 320–328
Gkisser, S. (2017). Predictive inference: an introduction. Chapman and Hall/CRC
Hamam, A., & Georganas, N. D. (2008). A comparison of Mamdani and Sugeno fuzzy inference systems for evaluating the quality of experience of Hapto-Audio-Visual applications. In 2008 IEEE International Workshop on Haptic Audio visual Environments and Games (pp. 87–92). IEEE
Hellas, A., Ihantola, P., Petersen, A., Ajanovski, V. V., Gutica, M., Hynninen, T. … Liao, S. N. (2018). Predicting academic performance: a systematic literature review. In Proceedings companion of the 23rd annual ACM conference on innovation and technology in computer science education (pp. 175–199). https://doi.org/10.1145/3293881.3295783
Hirokawa, S. (2018). Key attribute for predicting student academic performance. In Proceedings of the 10th International Conference on Education Technology and Computers (pp. 308–313)
Hutt, S., Gardener, M., Kamentz, D., Duckworth, A. L., & D’Mello, S. K. (2018). Prospectively predicting 4-year college graduation from student applications. In Proceedings of the 8th international conference on learning analytics and knowledge (pp. 280–289)
Jang, J. S. (1993). ANFIS: adaptive-network-based fuzzy inference system. IEEE transactions on systems man and cybernetics, 23(3), 665–685
Jain, L. C., & Martin, N. M. (Eds.). (1998). Fusion of neural networks, fuzzy systems and genetic algorithms: industrial applications (4 vol.). CRC press
Kaggle (2021). HSC Level Student’s GPA Dataset. https://www.kaggle.com/tahamidulislamsamin/final-training-data-project-gpa?select=test+data+rank.csv
Kohavi, R., & John, G. H. (1997). Wrappers for feature subset selection. Artificial intelligence, 97(1–2), 273–324
Koutina, M., & Kermanidis, K. L. (2011). Predicting postgraduate students’ performance using machine learning techniques. Artificial intelligence applications and innovations (pp. 159–168). Berlin, Heidelberg: Springer
Lagman, A. C., Calleja, J. Q., Fernando, C. G., Gonzales, J. G., Legaspi, J. B., Ortega, J. H. J. C. … Santos, R. C. (2019). Embedding naïve Bayes algorithm data model in predicting student graduation. In Proceedings of the 3rd international conference on telecommunications and communication engineering (pp. 51–56)
Lamy, D. (1996). Modeling and sensitivity analysis of neural networks. Mathematics and computers in simulation, 40(5–6), 535–548
Liao, S. N., Zingaro, D., Alvarado, C., Griswold, W. G., & Porter, L. (2019). Exploring the value of different data sources for predicting student performance in multiple cs courses. In Proceedings of the 50th ACM Technical Symposium on Computer Science Education (pp. 112–118). https://doi.org/10.1145/3287324.3287407
Liao, S. N., Zingaro, D., Thai, K., Alvarado, C., Griswold, W. G., & Porter, L. (2019). A robust machine learning technique to predict low-performing students. ACM transactions on computing education (TOCE), 19(3), 1–19. https://doi.org/10.1145/3277569
Mamdani, E. H. (1974). Application of fuzzy algorithms for control of simple dynamic plant. In Proceedings of the institution of electrical engineers (Vol. 121, No. 12, pp. 1585–1588). IET
Manrique, R., Nunes, B. P., Marino, O., Casanova, M. A., & Nurmikko-Fuller, T. (2019). An analysis of student representation, representative features and classification algorithms to predict degree dropout. In Proceedings of the 9th International Conference on Learning Analytics & Knowledge (pp. 401–410)
MathWorks (2021a). Documentation. https://www.mathworks.com/help/fuzzy/genfis.html
MathWorks (2021b). Documentation. https://www.mathworks.com/help/fuzzy/anfis.html?s_tid=srchtitle.
Mitra, S., & Hayashi, Y. (2000). Neuro-fuzzy rule generation: survey in soft computing framework. IEEE transactions on neural networks, 11(3), 748–768
Mosteller, F., & Tukey, J. W. (1977). Data Analysis and Regression. Reading, MA: Addison-Wesley
National Center for Education Statistics of the United States (2019). The Condition of Education 2019 (NCES 2019 – 144), Undergraduate Retention and Graduation Rates. https://nces.ed.gov/fastfacts/display.asp?id=40
Negnevitsky, M. (2005). Artificial Intelligence: A guide to intelligent systems. Addison Wesley.
Negnevitsky, M. (2017). Artificial Intelligence: A guide to intelligent systems. Addison Wesley
Okubo, F., Yamashita, T., Shimada, A., & Ogata, H. (2017). A neural network approach for students’ performance prediction. In Proceedings of the seventh international learning analytics & knowledge conference (pp. 598–599)
Pal, M., & Bharati, P. (2019). Introduction to correlation and linear regression analysis. Applications of Regression Techniques (pp. 1–18). Singapore: Springer
Papadogiannis, I., Poulopoulos, V., & Wallace, M. (2020). What has been done, what has been learnt and what remains to be seen. International Journal of Educational Research Review, 5(4), 353–372. A Critical Review of Data Mining for Education:
Pardo, A., Mirriahi, N., Martinez-Maldonado, R., Jovanovic, J., Dawson, S., & Gašević, D. (2016l). Generating actionable predictive models of academic performance. In Proceedings of the sixth international conference on learning analytics & knowledge (pp. 474–478)
Pérez, B., Castellanos, C., & Correal, D. (2018). Predicting student drop-out rates using data mining techniques: A case study. In IEEE Colombian Conference on Applications in Computational Intelligence (pp. 111–125). Springer, Cham. https://doi.org/10.1007/978-3-030-03023-0_10
Reddy, N. S., Lee, C. S., Kim, J. H., & Semiatin, S. L. (2006). Determination of the beta-approach curve and beta-transus temperature for titanium alloys using sensitivity analysis of a trained neural network. Materials Science and Engineering: A, 434(1–2), 218–226
Richardson, M., Abraham, C., & Bond, R. (2012). Psychological correlates of university students’ academic performance: a systematic review and meta-analysis. Psychological bulletin, 138(2), 353
Runbo, B., Jia, H. & Cao, P. (2011) Factor Sensitivity Analysis with Neural Network Simulation based on Perturbation System. Journal of Computers, 6(7), 1402-1407. 10.4304/jcp.6.7.1402-1407
Rustia, R. A., Cruz, M. M. A., Burac, M. A. P., & Palaoag, T. D. (2018). Predicting Student’s Board Examination Performance using Classification Algorithms. In Proceedings of the 2018 7th International Conference on Software and Computer Applications (pp. 233–237)
Rutkowski, L. (2004). Fuzzy Inference Systems. Flexible Neuro-Fuzzy Systems: Structures, Learning and Performance Evaluation (771 vol.). Boston, MA: Springer. The International Series in Engineering and Computer Science
Sekeroglu, B., Dimililer, K., & Tuncal, K. (2019). Student performance prediction and classification using machine learning algorithms. In Proceedings of the 2019 8th International Conference on Educational and Information Technology (pp. 7–11)
e Silva, I. H., Pacheco, O., & Tavares, J. (2003). Effects of curriculum adjustments on first-year programming courses: students’ performance and achievement. In Frontiers in Education Conference (Vol. 1, pp. T4C-10). STIPES
Sproule, B. A., Naranjo, C. A., & Türksen, I. B. (2002). Fuzzy pharmacology: theory and applications. Trends in Pharmacological Sciences, 23(9), 412–417
Sambariya, D. K., & Prasad, R. (2017). Selection of membership functions based on fuzzy rules to design an efficient power system stabilizer. International Journal of Fuzzy Systems, 19(3), 813–828
Shmueli, G. (2010). To explain or to predict? Statistical science, 25(3), 289–310
Stone, M. (1974). Cross-validatory choice and assessment of statistical predictions. Journal of the royal statistical society: Series B (Methodological), 36(2), 111–133
Stumpf, H., & Stanley, J. C. (2002). Group data on high school grade point averages and scores on academic aptitude tests as predictors of institutional graduation rates. Educational and Psychological Measurement, 62(6), 1042–1052
Subhedar, M., & Birajdar, G. (2013). Comparison of mamdani and sugeno inference systems for dynamic spectrum allocation in cognitive radio networks. Wireless personal communications, 71(2), 805–819
Tanaka, K., & Sugeno, M. (1998). Introduction to fuzzy modelling, in Fuzzy Systems: Modeling and Control, H. T. Nguyen and M. Sugeno, Eds. Kluwe
Terano, T., Asai, K., & Sugeno, M. (1994). Applied Fuzzy Systems. AP Professional
Tomkin, J. H., West, M., & Herman, G. L. (2018). An improved grade point average, with applications to CS undergraduate education analytics. ACM Transactions on Computing Education (TOCE), 18(4), 1–16
Voyer, D., & Voyer, S. D. (2014). Gender differences in scholastic achievement: a meta-analysis. Psychological bulletin, 140(4), 1174
Wang, W., Jones, P., & Partridge, D. (2000). Assessing the impact of input features in a feedforward neural network. Neural Computing & Applications, 9(2), 101–112
Waugh, G., Micceri, T., & Takalkar, P. (1994). Using Ethnicity, SAT/ACT Scores, and High School GPA To Predict Retention and Graduation Rates
Wei, D., & Burrows, A. N. (2016). Tracking students’ performance to assess correlations among computer science programming series courses. Journal of Computing Sciences in Colleges, 32(1), 9–16
Zeng, X., & Yeung, D. S. (2003). A quantified sensitivity measure for multilayer perceptron to input perturbation. Neural Computation, 15(1), 183–212
Zollanvari, A., Kizilirmak, R. C., Kho, Y. H., & Hernández-Torrano, D. (2017). Predicting students’ GPA and developing intervention strategies based on self-regulatory learning behaviors. Ieee Access : Practical Innovations, Open Solutions, 5, 23792–23802
Acknowledgements
The authors would like thank the College of Engineering and Information Technology for permitting the authors to use the datasets of the information technology and the computer engineering programs to conduct this work.
Funding
The authors have no relevant financial or non-financial interests to disclose.
Author information
Authors and Affiliations
Contributions
All authors contributed to the study conception and design. Material preparation, data collection and analysis were performed by Riyadh Mehdi, and Mirna Nachouki. The first draft of the manuscript was written by Riyadh Mehdi and all authors commented on previous versions of the manuscript. All authors read and approved the final manuscript.
Corresponding authors
Ethics declarations
Competing Interests
The authors have no competing interests to declare that are relevant to the content of this article.
Ethics approval
This work does not involve humans and/or animals.
Informed consent
This work does not involve human participants.
Animal Welfare
This work does not involve animals.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Mehdi, R., Nachouki, M. A neuro-fuzzy model for predicting and analyzing student graduation performance in computing programs. Educ Inf Technol 28, 2455–2484 (2023). https://doi.org/10.1007/s10639-022-11205-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10639-022-11205-2