Location via proxy:   [ UP ]  
[Report a bug]   [Manage cookies]                
  • Open Access

Quantum Gravity in the Lab. II. Teleportation by Size and Traversable Wormholes

Sepehr Nezami, Henry W. Lin, Adam R. Brown, Hrant Gharibyan, Stefan Leichenauer, Grant Salton, Leonard Susskind, Brian Swingle, and Michael Walter
PRX Quantum 4, 010321 – Published 27 February 2023
PDFHTMLExport Citation
Abstract
Corrections
Authors
Popular Summary
See Also
Article Text
  • INTRODUCTION
  • EXAMPLE SYSTEMS
  • THE HOLOGRAPHIC INTERPRETATION
  • DISCUSSION AND OUTLOOK
  • ACKNOWLEDGMENTS
  • APPENDICES
    • References

    Abstract

    In Brown et al. [PRX Quantum, 4, 010321 (2023)], we discuss how holographic quantum gravity may be simulated using quantum devices and we give a specific proposal—teleportation by size and the phenomenon of size winding. Here, we elaborate on what it means to do quantum gravity in the lab and how size winding connects to bulk gravitational physics and traversable wormholes. Perfect size winding is a remarkable fine-grained property of the size wave function of an operator; we show from a bulk calculation that this property must hold for quantum systems with a nearly AdS2 bulk. We then examine in detail teleportation by size in three systems—the Sachdev-Ye-Kitaev model, random matrices, and spin chains—and discuss prospects for realizing these phenomena in near-term quantum devices.

    • Figure
    • Figure
    • Figure
    • Figure
    • Figure
    • Figure
    • Figure
    7 More
    • Received 24 October 2021
    • Revised 2 November 2022
    • Accepted 23 December 2022
    • Corrected 17 May 2023

    DOI:https://doi.org/10.1103/PRXQuantum.4.010321

    Published by the American Physical Society under the terms of the Creative Commons Attribution 4.0 International license. Further distribution of this work must maintain attribution to the author(s) and the published article's title, journal citation, and DOI.

    Published by the American Physical Society

    Physics Subject Headings (PhySH)

    1. Research Areas
    Quantum algorithmsQuantum entanglementQuantum gravityQuantum teleportation
    Quantum Information, Science & TechnologyGravitation, Cosmology & Astrophysics

    Corrections

    17 May 2023

    Correction: The source information for the companion paper in the first sentence of the abstract was inserted incorrectly during the proof cycle and has been set right.

    Authors & Affiliations

    Sepehr Nezami1,2,3, Henry W. Lin2,4, Adam R. Brown2,3,5, Hrant Gharibyan1,*, Stefan Leichenauer2,6, Grant Salton7,8,1,3, Leonard Susskind3,2,5, Brian Swingle9,10, and Michael Walter11,12

    • 1Institute for Quantum Information and Matter, Caltech, Pasadena, California 91125, USA
    • 2Google, Mountain View, California 94043, USA
    • 3Department of Physics, Stanford University, Stanford, California 94305, USA
    • 4Physics Department, Princeton University, Princeton, New Jersey 08540, USA
    • 5Blueshift, Alphabet, Mountain View, California 94043, USA
    • 6Sandbox@Alphabet, Mountain View, California 94043, USA
    • 7Amazon Quantum Solutions Lab, Seattle, Washington 98170, USA
    • 8Amazon Web Services (AWS) Center for Quantum Computing, Pasadena, California 91125, USA
    • 9Brandeis University, Waltham, Massachusetts 02453, USA
    • 10University of Maryland, College Park, Maryland 20742, USA
    • 11Faculty of Computer Science, Ruhr University Bochum, D-44801 Bochum, Germany
    • 12Korteweg–de Vries Institute for Mathematics, Institute for Theoretical Physics, Institute for Logic, Language and Computation & QuSoft, University of Amsterdam, 1090 GE Amsterdam, Kingdom of the Netherlands

    • *hrant@caltech.edu

    Popular Summary

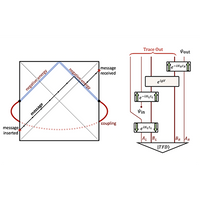
    In a companion work, we discuss how quantum gravity may be simulated using quantum devices and we introduce a specific proposal called teleportation by size that can be implemented with near-term quantum devices. Teleportation by size is a form of quantum teleportation inspired by particles traveling through a traversable wormhole in holographic theories of quantum gravity known as the anti–de Sitter – conformal field theory (AdS-CFT) correspondence.

    Here, we elaborate further on what it means to do “quantum gravity in the lab” and we demonstrate the teleportation-by-size protocol for systems with scrambling dynamics. We also discuss how the quantum dynamics of the protocol connect to bulk gravitational physics and traversable wormholes through a surprising link between the “size” of operators in the quantum system and the momentum of infalling particles in the dual gravitational theory. We examine in detail teleportation by size in three systems: the Sachdev-Ye-Kitaev (SYK) model, random matrices, and spin chains. We also provide further clarifications on the prospects for realizing these phenomena in near-term quantum devices.

    Key Image

    See Also

    Quantum Gravity in the Lab. I. Teleportation by Size and Traversable Wormholes

    Adam R. Brown, Hrant Gharibyan, Stefan Leichenauer, Henry W. Lin, Sepehr Nezami, Grant Salton, Leonard Susskind, Brian Swingle, and Michael Walter
    PRX Quantum 4, 010320 (2023)

    Article Text

    Click to Expand

    References

    Click to Expand
    Issue

    Vol. 4, Iss. 1 — February - April 2023

    Reuse & Permissions
    Author publication services for translation and copyediting assistance advertisement

    Authorization Required

    Log In
    Other Options
    ×

    Images

    • Figure 1
      Figure 1

      The refinement of size-momentum duality to the level of wave functions. If the expansion of the time-evolved thermal Pauli (or fermion) is ρβ1/2P(t)=∑cPP (or ρβ1/2ψ(t)=∑cuΨu), then one can define the winding size distribution q(l)=∑|P|=lcp2 (or q(l)=∑|u|=lcu2), in contrast to the conventional size distribution ∑|P|=l|cp|2. We argue that the ql is the boundary analog of the bulk momentum wave function. The plot is the schematic drawing of the winding size distribution in the SYK model, near, but slightly before, the scrambling time. This is the regime where the width of the distribution is of order n. One can observe that the Fourier transform of the winding size distribution mimics the behavior of the position of the infalling particle (measured, e.g., from the black-hole horizon). Top center: the magnitude and phase of the winding size distribution. Bottom center: the Fourier transform (or bulk location) is near the origin. Top left: the magnitude and phase of the winding size distribution at a slightly earlier time. The size distribution is smaller and winds faster. Bottom left: the Fourier transform (or bulk location) is further from the origin. Top right: the size distribution after acting by eigV, with the proper value of g. The distribution is now winding in the opposite direction. Bottom right: the Fourier transform shows that the particle is on the other side of the origin, a manifestation of the fact that the infalling particle has moved from one side of the horizon to the other side.

      Reuse & Permissions
    • Figure 2
      Figure 2

      A short summary of teleportation by size, discussing different systems, different patterns of operator growth, and the consequence of each growth pattern for signal transmission. (a) Operator growth, late time, most quantum systems: teleports one qubit through state-transfer mechanism; sgn(g) independent; infinite temperature. (b) Operator growth, intermediate time: chaotic spin chains, random circuits; teleports many qubits through state-transfer mechanism; sgn(g) independent; infinite temperature. (c) Size winding (damped), low temperature: teleports through state-transfer mechanism; weak sgn(g) dependence; works weakly for “operator transfer.” (d) Perfect size winding (not damped), low temperature: could teleport through state-transfer mechanism; strong sgn(g) dependence but limited fidelity; works perfectly for “operator transfer” slightly before scrambling time; strong signature of a geometrical wormhole. Blue, initial operator-size distribution; red, operator-size distribution of the time-evolved operator.

      Reuse & Permissions
    • Figure 3
      Figure 3

      The Penrose diagram of wormholes. Left: without the coupling, a message or particle inserted at early times on the left passes through the left horizon and hits the singularity (the top line of the diagram). Right: in the presence of the left-right coupling, the message hits the negative-energy shock wave (the thick blue line) created by the coupling. The effect of the collision is to rescue the message from behind the right horizon.

      Reuse & Permissions
    • Figure 4
      Figure 4

      The circuits considered in this paper, with HL=HRT. Downward arrows indicate acting with the inverse of the time-evolution operator. In both protocols, the goal is to transmit information from the left to the right. (a) The state-transfer protocol calls for us to discard the left message qubits (AL) and replace them with our message Ψin. The output state on the right then defines a channel applied to the input state. (b) The operator-transfer protocol calls for the operator O to be applied to AL. Based on the choice of operator, the output state on the right is modified, similar to a perturbation-response experiment.

      Reuse & Permissions
    • Figure 5
      Figure 5

      Traversing the wormhole from the boundary point of view. (a) An operator O inserted at negative time t into the left boundary. (b) The (winding) size distribution of the thermal operator O(t)ρβ1/2, which is winding in the clockwise direction. (c) The size distribution after the application of LR coupling. The coupling applies a linear phase to the size distribution of the thermal operator in (b), unwinds it, and winds it in the opposite direction. In this way, we obtain a counterclockwise size distribution corresponding to the thermal operator ρβ1/2O(t). (d) As we see in Ref. [4], winding in the opposite direction corresponds to the operator inserted on the other boundary at a positive time. Thus, the coupling maps the operator O on the left to operator OT on the right.

      Reuse & Permissions
    • Figure 6
      Figure 6

      Analytical results for the infinite-temperature state-transfer protocol for sending one qubit (m=1), when the Hamiltonian is coming from the GOE and at g=π. The average channel always has the form of a depolarizing channel with parameter λ, conjugated by Pauli Y (see Eq. (3) in Ref. [4]). A small λ corresponds to a degraded signal, while λ=1 indicates perfect transmission. Top left: the plot of λ when the sending time −tL is the same as the probing time tR. Top right: the plot of λ as a function of the probing time tR, when −tL=−1. A weak signal comes out at tR≃2. Bottom left: the plot of λ as a function of the probing time tR, when −tL=−3. A strong signal is observed at tR=3. Bottom right: the plot of λ as a function of the probing time tR, when −tL=−7. After the scrambling time, the probed signal is maximized at tR=tL.

      Reuse & Permissions
    • Figure 7
      Figure 7

      A teleportation channel with a random Hamiltonian at β=20. Top left: the GOE Hamiltonian depolarizing parameter λ. It clearly shows an improvement in the fidelity and quality of the channel for positive g. Top right: |q~(g)| for the GUE Hamiltonian [recall that q~(g)≈e−ig⟨T|PR(t)eigVPLT(−t)|T⟩; see Eq. (12) of Ref. [4] ]. The phenomenon of size winding modifies the value of the two-point function |q~(g)| for early times in a sign(g)-dependent way. Bottom left: the imaginary part of C=⟨e−igVϕL(−t)eigVϕR(t)⟩. ImC is the value of the commutator of left and right, an indicator of the causal signal. Bottom right: |q~(g)| as a function of g at t=1. It shows a clear asymmetry around g=0 at low temperatures.

      Reuse & Permissions
    • Figure 8
      Figure 8

      (a) A snapshot of the time evolution of a one-dimensional random local circuit. (b) The circuit scrambles the degrees of freedom locally and, intuitively, it looks like a stack of parallel random unitaries (the green boxes), with the length scale given by the size of the light cone. Teleportation by size for random unitaries teaches us that we can use each individual random unitary as a resource teleporting exactly one qubit (teleporting qubits indicated by dark green circles, while the ZZ coupling acts on other qubits). (c) As time passes, the random boxes start to grow and recombine. Hence, the number of available boxes, and consequently the number of teleported qubits, will decrease.

      Reuse & Permissions
    • Figure 9
      Figure 9

      An analytical evaluation of the size distribution of 2-local Brownian circuits on n=400 qubits. The operator starts small and its evolved size is plotted for a different range of times. At t=1, the operator size is still small. Then, it becomes wider until t≃1.6 and starts to reconcentrate to the final value afterward. The final width is a function of n and the peak is sharper for larger n (this is because at late times the time-evolved Pauli looks like a random string of single-qubit Pauli operators.). However, the width of the size distribution at the intermediate times only weakly depends on n (for evidence, see Fig. 14).

      Reuse & Permissions
    • Figure 10
      Figure 10

      The action of P+ (left) and P− (right) in AdS2. These generators act by shifting Poincare time. The particle in the right diagram would experience a null shift when leaving the Poincare patch (shaded in pink). We also indicate in the right diagram the horizon (dotted black line) and the nearly AdS2 boundaries (solid black segments). Note that with our conventions, physical future-directed quanta satisfy P+<0, P−<0. Here, we are thinking of P+ and P− as being generated by operators at tL=tR=0. By boosting these operators, we can obtain generators that act at tR=−tL=t. For large values of t, this gives us the null generators at the horizon.

      Reuse & Permissions
    • Figure 11
      Figure 11

      Teleportation at the end of the world. In this modified protocol, we insert a particle on the left at some time tL=−t. Unlike the protocol in Ref. [5], t could be arbitrarily close to zero. The green trajectories show the standard evolution by HL+HR. A particle (wavy gray line) inserted on the left does not make it to the green boundary on the right. If we instead evolve with the symmetry generator P+~, the boundary particle on the right follows a trajectory of constant Poincare distance (dark red). The particle will then intersect the trajectory. Note that the point on the left indicated by the blue circle is a fixed point of the Poincare symmetry. When we evolve by P+, the interpretation is that the left boundary is fixed at this space-time point. Alternatively, we may project onto an eigenbasis of the Pauli Zi operators by performing a complete measurement on the left-hand side. This inserts an EoW brane [37].

      Reuse & Permissions
    • Figure 12
      Figure 12

      The entanglement wedge of the garbage is displayed in blue. The entanglement wedge of the right system plus m qubits on the left is displayed in pink. Left: when m=0, the garbage contains the whole left side, so the quantum extremal surface is just the horizon. Center: as we decrease the size of the garbage, the island shrinks. Right: m=n. The entanglement wedge of the pink region extends all the way to the left boundary.

      Reuse & Permissions
    • Figure 13
      Figure 13

      A plot of the teleportation signal λ(t,t) as defined in Eq. (C3), for a Hamiltonian coming from the GOE. This is plotted for g=π.

      Reuse & Permissions
    • Figure 14
      Figure 14

      The Brownian-circuit operator growth as function of the number of qubits and the initial time.

      Reuse & Permissions
    ×

    Sign up to receive regular email alerts from PRX Quantum

    Reuse & Permissions

    It is not necessary to obtain permission to reuse this article or its components as it is available under the terms of the Creative Commons Attribution 4.0 International license. This license permits unrestricted use, distribution, and reproduction in any medium, provided attribution to the author(s) and the published article's title, journal citation, and DOI are maintained. Please note that some figures may have been included with permission from other third parties. It is your responsibility to obtain the proper permission from the rights holder directly for these figures.

    ×

    Log In

    Cancel
    ×

    Search

    Article Lookup

    Paste a citation or DOI
    Enter a citation
    ×