Location via proxy:   [ UP ]  
[Report a bug]   [Manage cookies]                
  • Open Access

Quantum Fourier Transform Has Small Entanglement

Jielun Chen (陈捷伦), E.M. Stoudenmire, and Steven R. White
PRX Quantum 4, 040318 – Published 27 October 2023
PDFHTMLExport Citation
Abstract
Authors
Popular Summary
Article Text
  • INTRODUCTION
  • EXPONENTIAL DECAY OF THE QFT’S SCHMIDT…
  • MATRIX PRODUCT OPERATOR FORM OF THE QFT
  • APPLICATION: QFT VERSUS THE FFT
  • CONCLUSION
  • ACKNOWLEDGMENTS
  • APPENDICES
    • References

    Abstract

    The quantum Fourier transform (QFT) is a key component of many important quantum algorithms, most famously being the essential ingredient in Shor’s algorithm for factoring products of primes. Given its remarkable capability, one would think it can introduce large entanglement to qubit systems and would be difficult to simulate classically. While early results showed the QFT indeed has maximal operator entanglement, we show that this is entirely due to the bit reversal in the QFT. The core part of the QFT has Schmidt coefficients decaying exponentially quickly, and thus it can generate only a constant amount of entanglement regardless of the number of qubits. In addition, we show the entangling power of the QFT is the same as the time evolution of a Hamiltonian with exponentially decaying interactions, and thus a variant of the area law for dynamics can be used to understand the low entanglement intuitively. Using the low entanglement property of the QFT, we show that classical simulations of the QFT on a matrix product state with low bond dimension take time linear in the number of qubits, providing a potential speedup over the classical fast Fourier transform on many classes of functions. We demonstrate this speedup in test calculations on some simple functions. For data vectors of length 106–108, the speedup can be a few orders of magnitude.

    • Figure
    • Figure
    • Figure
    • Figure
    • Figure
    • Figure
    • Figure
    2 More
    • Received 2 January 2023
    • Accepted 25 September 2023

    DOI:https://doi.org/10.1103/PRXQuantum.4.040318

    Published by the American Physical Society under the terms of the Creative Commons Attribution 4.0 International license. Further distribution of this work must maintain attribution to the author(s) and the published article's title, journal citation, and DOI.

    Published by the American Physical Society

    Physics Subject Headings (PhySH)

    1. Research Areas
    Entanglement entropyEntanglement measuresEntanglement productionQuantum algorithms & computationQuantum circuitsQuantum computationQuantum correlations in quantum informationQuantum correlations, foundations & formalismQuantum entanglementQuantum information theory
    1. Techniques
    Matrix product statesTensor network methods
    Quantum Information, Science & TechnologyEnergy Science & Technology

    Authors & Affiliations

    Jielun Chen (陈捷伦)1,2,*, E.M. Stoudenmire3, and Steven R. White1

    • 1Department of Physics and Astronomy, University of California, Irvine, California 92697-4575, USA
    • 2Department of Physics, California Institute of Technology, Pasadena, California 91125, USA
    • 3Center for Computational Quantum Physics, Flatiron Institute, 162 Fifth Avenue, New York, New York 10010, USA

    • *jchen9@caltech.edu

    Popular Summary

    The quantum Fourier transform (QFT) is a cornerstone quantum algorithmic primitive. Quantum algorithms employing the QFT (for example, Shor’s algorithm) are likely exponentially faster than their classical counterparts. Given the QFT’s ability, it is likely that it generates large quantum entanglement and is hard to simulate classically. Surprisingly, we show that, with certain qubit ordering, the QFT has small entanglement and compresses into an efficient classical representation. We can even use this property to build a “quantum-inspired” classical algorithm to accelerate the fast Fourier transform (FFT) in certain situations.

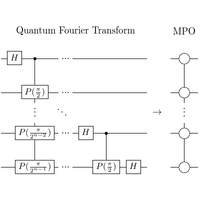
    In particular, we investigate the QFT’s entanglement through Schmidt decomposition. We show that, if the input and output have reversed qubit ordering, its Schmidt coefficients are bounded by exponentially small numbers, implying its compressibility into a matrix product operator (MPO). We prove the bound by mapping to a well-studied problem in signal processing, and we provide an intuitive explanation through connections to dynamical area laws. We then show that using the MPO framework, one can achieve speedup compared to FFT in certain regimes, even when the input is an exponentially long vector.

    Our result could potentially lead to novel classical Fourier transform algorithms, better implementation of the QFT on a quantum computer, as well as new theoretical understandings of quantum algorithms and quantum information.

    Key Image

    Article Text

    Click to Expand

    References

    Click to Expand
    Issue

    Vol. 4, Iss. 4 — October - December 2023

    Reuse & Permissions
    Author publication services for translation and copyediting assistance advertisement

    Authorization Required

    Log In
    Other Options
    ×

    Images

    • Figure 1
      Figure 1

      A 4-qubit example of the QFT circuit, i.e., Fn with n=4, consisting of two parts, Qn and the bit-reversal operation Rn. Qn can be decomposed into Hadamard gates and controlled phase gates, with definitions of each given at the bottom.

      Reuse & Permissions
    • Figure 2
      Figure 2

      A 4-qubit example of the generalized recursive circuit of Qn, i.e., Ωn,j sandwiched by two smaller QFT circuits, Qj and Qn−j. While in this example we choose j=n/2=2, this decomposition works for any j.

      Reuse & Permissions
    • Figure 3
      Figure 3

      Contracting a 4-qubit QFTTN into a QFT MPO. In step 1, we contract the first two phase MPOs by doing a series of SVDs and we truncate small singular values or keep χ of them. Since site 1 is isometric already by contraction of the H tensor and the copy tensor, we stop at site 2, and thus the orthogonality center at the end is at site 2. In step 2, we do a series of SVDs to push the orthogonality center to the last site, and again we truncate singular values or keep χ singular values. In step 3, we repeat the contraction for our current MPO and the next phase MPO. During the steps, we also contract any H tensors encountered. The final MPO has the orthogonality center at site 3.

      Reuse & Permissions
    • Figure 4
      Figure 4

      Time to compute the discrete Fourier transform with use of either the FFT algorithm for data of size 2n or the QFT MPO acting on various functions represented as an MPS with n sites (qubits). Dashed curves include the time to convert the data to the MPS format with use of a randomized SVD (RSVD) algorithm plus the application of the QFT, while solid curves represent the time of the QFT step only. Timings were performed with a 2021 ten-core MacBook Pro with an M1 Max processor with use of fftw and ITensor [41].

      Reuse & Permissions
    • Figure 5
      Figure 5

      The orthogonal property of a QFTTN. By our treating each sequence of tensors acting on the same qubit as a single tensor, the QFTTN corresponds to a right-canonical MPO with bond dimension unoptimized (here “right” means “down” in the orientation of the quantum circuit). In this 4-qubit example, the orthogonal property of U3 is shown, and U1 and U2 obey the same identity, but T4 does not and thus it is the orthogonality center.

      Reuse & Permissions
    • Figure 6
      Figure 6

      (a) Example of partitioning a 6-qubit QFTTN at the center into two sets of tensors A and B. (b) Simplifying the calculation of Schmidt coefficients. MA and MB represent tensors in panels A and B, respectively, in (a). Since all tensors in MA are isometric, singular values can be calculated only from MB.

      Reuse & Permissions
    • Figure 7
      Figure 7

      Simplifying matrix elements of MBMB†, with MB shown in Fig. 6. The first diagram to the second diagram is due to all H gates and phase gates being unitaries. The second diagram to the third diagram uses Eqs. (F11) and (F12). The third diagram to the fourth diagram uses Eq. (F8). The fourth diagram to the last diagram uses Eq. (F8) again and writes x=22x1+2x2+x3 and y=22y1+2y2+y3.

      Reuse & Permissions
    • Figure 8
      Figure 8

      Example of simpliying MBMB† to 2nFn,jFn,j† with n=6 and j=3. The diagram on the left comes from step 2 in Fig. 7.

      Reuse & Permissions
    • Figure 9
      Figure 9

      Diagrammatic illustration on how emax(Dn,jχ) are related for different n and j. The horizontal lines denote that the error on bond j has an upper bound independent of n, which is evident from Eq. (J16). The diagonal lines arise from the symmetry of the QFT, i.e., the Schmidt coefficients are identical at cuts j and n−j. Therefore, one can form a path between two bonds at any n and j; thus, the upper bound on emax(Dn,jχ) is also independent of j.

      Reuse & Permissions
    ×

    Sign up to receive regular email alerts from PRX Quantum

    Reuse & Permissions

    It is not necessary to obtain permission to reuse this article or its components as it is available under the terms of the Creative Commons Attribution 4.0 International license. This license permits unrestricted use, distribution, and reproduction in any medium, provided attribution to the author(s) and the published article's title, journal citation, and DOI are maintained. Please note that some figures may have been included with permission from other third parties. It is your responsibility to obtain the proper permission from the rights holder directly for these figures.

    ×

    Log In

    Cancel
    ×

    Search

    Article Lookup

    Paste a citation or DOI
    Enter a citation
    ×