Location via proxy:   [ UP ]  
[Report a bug]   [Manage cookies]                
  • Open Access

Universal Geometric Path to a Robust Majorana Magic Gate

Torsten Karzig, Yuval Oreg, Gil Refael, and Michael H. Freedman
Phys. Rev. X 6, 031019 – Published 8 August 2016
PDFHTMLExport Citation
Abstract
Authors
Popular Summary
Article Text
  • INTRODUCTION AND MAIN RESULTS
  • π/8 GATE IN AN IDEALIZED SYSTEM
  • SYSTEMATIC ERROR ELIMINATION USING…
  • DYNAMICAL PHASE ERROR AND ITS…
  • RETARDATION EFFECTS ELIMINATION USING…
  • NUMERICAL SIMULATION OF THE π/8 GATE
  • SUMMARY AND DISCUSSION
  • ACKNOWLEDGMENTS
  • APPENDICES
    • References

    Abstract

    A universal quantum computer requires a full set of basic quantum gates. With Majorana bound states one can form all necessary quantum gates in a topologically protected way, bar one. In this paper, we present a scheme that achieves the missing, so-called, π/8 magic phase gate without the need of fine-tuning for distinct physical realizations. The scheme is based on the manipulation of geometric phases described by a universal protocol and converges exponentially with the number of steps in the geometric path. Furthermore, our magic gate proposal relies on the most basic hardware previously suggested for topologically protected gates, and can be extended to an any-phase gate, where π/8 is substituted by any α.

    • Figure
    • Figure
    • Figure
    • Figure
    • Figure
    • Figure
    • Figure
    1 More
    • Received 16 December 2015

    DOI:https://doi.org/10.1103/PhysRevX.6.031019

    This article is available under the terms of the Creative Commons Attribution 3.0 License. Further distribution of this work must maintain attribution to the author(s) and the published article’s title, journal citation, and DOI.

    Published by the American Physical Society

    Physics Subject Headings (PhySH)

    1. Research Areas
    Majorana fermionsQuantum computationTopological quantum computing
    Quantum Information, Science & Technology

    Authors & Affiliations

    Torsten Karzig1,2,3, Yuval Oreg4, Gil Refael1,2, and Michael H. Freedman3,5

    • 1Walter Burke Institute for Theoretical Physics and Institute for Quantum Information and Matter, California Institute of Technology, Pasadena, California 91125, USA
    • 2Department of Physics, California Institute of Technology, Pasadena, California 91125, USA
    • 3Station Q, Microsoft Research, Santa Barbara, California 93106-6105, USA
    • 4Department of Condensed Matter Physics, Weizmann Institute of Science, Rehovot, 76100 Israel
    • 5Department of Mathematics, University of California, Santa Barbara, California 93106, USA

    Popular Summary

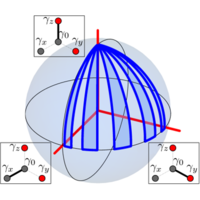
    The vision behind topological quantum computation involves employing simple braiding operations of non-Abelian quasiparticles in two-dimensional systems in order to carry out quantum gates. The resulting quantum information will then be protected since it will be encoded in the topological properties of the quantum state in a way that is spread out over an entire system and inaccessible to any local disturbance or measurement. Majorana bound states are by far the simplest, non-Abelian quasiparticles known, and they have already been realized experimentally. Unfortunately, the braiding operations of Majorana states are not enough to build a full-fledged quantum computer. The remaining ingredient that would unlock full quantum universality is a so-called magic gate (or π/8 gate) that corresponds to an exact superposition of doing and not doing an exchange between two Majoranas. Not being able to carry out this gate in a protected way is a major hindrance to topological quantum computing. Here, we offer a resolution for this problem and explain how to perform a magic gate without any fine-tuning.

    We consider a setup of four Majoranas and show that such a magic gate results from combining noise-canceling methods of quantum control with the underlying topological protection of Majorana states. Our scheme requires no special hardware beyond what is expected for all other necessary gates. By sweeping back and forth in the (geometric) parameter space that defines the gate operation, errors due to experimental imperfections drop exponentially in the number of sweeps. This “geometric decoupling” significantly enhances the quantum-control toolbox of Majoranas, providing novel pathways for exponentially and universally protected gates.

    We expect that our findings will pave the way for magic-gate schemes that can be realized for many types of environmental noise.

    Key Image

    Article Text

    Click to Expand

    References

    Click to Expand
    Issue

    Vol. 6, Iss. 3 — July - September 2016

    Subject Areas
    Reuse & Permissions
    Author publication services for translation and copyediting assistance advertisement

    Authorization Required

    Log In
    Other Options
    ×

    Images

    • Figure 1
      Figure 1

      The Y-junction system. Lines and labels indicate the model Hamiltonian of four coupled Majoranas γi, while the background shows a possible realization using wires (gray) proximity coupled to s-wave superconductors (green). We assume that couplings at the arms are determined through external imprecise controls. The true couplings are Δ→=δ→+f→(δ→). It is indeed beneficial to think of the coupling to the x, y, and z arms as geometric objects, namely, vectors in a three-dimensional space. In addition to the couplings along the arms, any physical system will also exhibit couplings between the tips (dashed blue lines). These unavoidable couplings introduce a parity-dependent dynamical phase, and, along with the control uncertainty, are leading sources of error.

      Reuse & Permissions
    • Figure 2
      Figure 2

      A visualization of the exchange process as the turning arm of a clock. First, Δz≫Δx,Δy, to indicate that the line presenting the coupling between γ0 and γz is bold. Then, Δy≫Δx,Δz, then Δx≫Δy,Δz, and finally, Δz≫Δx,Δy again, so that the arm of the clock completes a full turn. This process can also be visualized as a line covering an octant on a unit sphere. The Berry phase difference of the two parity sectors accumulated in this process is equal to the covered solid angle, −π/2. We show in the text (see Appendix pp1) that this gives rise to a −π/4 phase gate, meaning a phase ∓π/4 for each fusion channel. (The minus sign appears due to the clockwise orientation of the trajectory and the convention we chose.) Since we can make one of the coupling constants exponentially smaller than the other two, the trajectory in the parameter space is glued to the edges of the octant making the accumulated Berry phase difference equal to −π/2 with exponential accuracy.

      Reuse & Permissions
    • Figure 3
      Figure 3

      The sequence for a π/8 gate in the ideal Y-junction system. This trajectory is not protected as we have to keep Δx=Δy while modifying Δz; small fluctuations will yield a different phase. This trajectory corresponds to a split of one of the Majoranas to two and an exchange of the position of another Majorana with only half of the split Majorana.

      Reuse & Permissions
    • Figure 4
      Figure 4

      The vertical snake contour. A proper choice of the turning point ϕnN yields a trajectory covering a solid angle of π/4 with an exponentially small error. Here, we plot the contour for the Chebyshev polynomials with N=5 and ϕnN=(π/2)xnN, and xnN,n=1,…,2N, are given in Eq. (15).

      Reuse & Permissions
    • Figure 5
      Figure 5

      Numerical demonstration of the robustness of the π/8 gate. (a) Systematic deviation of the angle Φ from its perfect implementation ϕ (dashed black line). The corresponding modified contour for N=4 (solid blue line) is depicted in (b) and shows clear variations from the perfect implementation (dashed black line). (c) The relative error in the phase gate angle δα, which decays exponentially with the number of turns N. (The dashed red line shows the exponential fit.) (d),(e) Effect of a finite outer coupling [ϵ=0.001, cf. Eq. (17)] without and with an accompanying parity echo (see Sec. 4). (f) An imperfect echo implementation where ϵ changes by δϵ=0.01ϵ between the echo sequences.

      Reuse & Permissions
    • Figure 6
      Figure 6

      The horizontal snake contour. A proper choice of the turning point θnN yields a solid angle of π/4 with an exponentially small error. Here, we show the contour based on Chebyshev polynomials with N=4 and cosθnN=xnN, and xnN,n=1,…,2N, are given in Eq. (15).

      Reuse & Permissions
    • Figure 7
      Figure 7

      Underlying substructure of the setup in Fig. 1. The central Majorana mode γ0 emerges from the low-energy subspace of three strongly coupled Majoranas γ˜i.

      Reuse & Permissions
    • Figure 8
      Figure 8

      Effect of cross-correlations between Φ and θ on the geometric decoupling scheme. (a) The modified protocol (solid blue) described by the error model [Eq. (g2)] in comparison to the perfect implementation (dashed black). (b) Decay of the phase error in terms of the number of turns N. The red dashed line shows an exponential fit starting at N=5.

      Reuse & Permissions
    ×

    Sign up to receive regular email alerts from Physical Review X

    Reuse & Permissions

    It is not necessary to obtain permission to reuse this article or its components as it is available under the terms of the Creative Commons Attribution 3.0 License. This license permits unrestricted use, distribution, and reproduction in any medium, provided attribution to the author(s) and the published article's title, journal citation, and DOI are maintained. Please note that some figures may have been included with permission from other third parties. It is your responsibility to obtain the proper permission from the rights holder directly for these figures.

    ×

    Log In

    Cancel
    ×

    Search

    Article Lookup

    Paste a citation or DOI
    Enter a citation
    ×