Wellenlängenoptimierung bei Heterodyn-Phasenschiebeverfahren

1 Einleitung

Zur flächenhaften Erfassung von Werkstückoberflächen kommen heute oftmals optisch antastende Systeme zum Einsatz, bei welchen das Werkstück von einer oder mehreren elektronischen Kameras aufgezeichnet wird. Abhängig vom Messprinzip ist es hierbei erforderlich, eine optische Ortskodierung im Objektraum vorzunehmen. Prominenteste Beispiele entsprechender Systeme sind die sogenannten Streifenprojektionssensoren, bei welchen die zu erfassende Oberfläche mittels strukturierter Beleuchtung optisch kodiert wird, um in der Folge homologe Bildpunkte identifizieren und die Oberfläche mittels Triangulation rekonstruieren zu können [1]. Hinsichtlich der angewendeten Grundtechniken verwandt ist der Streifenprojektion die phasenmessende Deflektometrie, bei welcher jedoch nicht das Werkstück selbst, sondern eine im Raum verkörperte Referenzstruktur mit einer optischen Kodierung beaufschlagt wird [2], [3].

Zur flächenhaften optischen Kodierung können grundsätzlich die unterschiedlichsten Muster eingesetzt werden, jedoch erweist sich als die verbreitetste, weil potentiell genaueste Technik die Kodierung mittels Phasenschiebeverfahren unter Verwendung sinusförmiger Streifenmuster [1]. Aufgrund der Periodizität dieser Streifenmuster ist jedoch allein mit einer Phasenschiebeauswertung noch keine im gesamten Messbereich eindeutige Ortskodierung möglich, sondern der Eindeutigkeitsbereich der Phasenmessung erstreckt sich zunächst nur über eine Periode des zugrunde liegenden Sinusmusters. Um diese Mehrdeutigkeit aufzulösen, muss ein geeignetes Entfaltungsverfahren angewendet werden. Im Bereich der strukturierten Beleuchtung kommen meist zeitliche Entfaltungsverfahren zur Anwendung, die auf der Aufzeichnung zusätzlicher Mustersequenzen basieren. Einen in der Gesamtheit seiner Eigenschaften besonders vorteilhaften Ansatz hierzu stellt das sogenannte Heterodynverfahren dar, welches auf der sequenziellen Aufzeichnung mehrerer Phasenschiebesequenzen leicht unterschiedlicher Periodenlänge basiert [4].

Bei der praktischen Umsetzung des Heterodynverfahrens stellt sich unweigerlich die Frage, wie die Wellenlängen der verwendeten Sinusmuster gewählt werden sollten, um möglichst zuverlässige Ergebnisse zu erzielen. Gegenstand des vorliegenden Beitrags ist es, hierzu mathematisch fundierte aber zugleich anwendungsnahe Kriterien zu formulieren, die geeignet sind, sowohl die Robustheit des Verfahrens im Sinne der Vermeidung von Entfaltungsfehlern zu optimieren, als auch die statistische Unsicherheit der resultierenden Ortskodierung zu minimieren. Hierzu wird in Abschnitt 2 zunächst allgemein auf die Grundlagen von Phasenschiebe- und Entfaltungsverfahren eingegangen, bevor in Abschnitt 3 eine für die weiteren Betrachtungen zugrunde gelegte, vorteilhafte Ausführungsform des Heterodynverfahrens vorgestellt wird, wie sie insbesondere für die Streifenprojektion oder die phasenmessende Deflektometrie angewendet werden kann. Aufbauend hierauf erfolgt in Abschnitt 4 eine kurze Beschreibung der auftretenden Entfaltungsfehler, ehe in Abschnitt 5 eine detaillierte statistische Analyse des Entfaltungsprozesses durchgeführt wird und Kriterien zur Minimierung der Auftretenswahrscheinlichkeit der unterschiedlichen Arten von Entfaltungsfehlern formuliert werden. Ergänzend hierzu wird in Abschnitt 6 eine experimentelle Methode zur aufgabenspezifischen Bestimmung der hinsichtlich der statistischen Unsicherheit der Ortskodierung optimalen Basiswellenlänge vorgestellt.

2 Phasenschiebe- und Entfaltungsverfahren

Die Orts- oder Abstandskodierung unter Verwendung sinusförmig modulierter Signale ist ein in vielen Bereichen der Messtechnik etabliertes Verfahren, welches abhängig vom eingesetzten Messprinzip unterschiedliche Erscheinungsformen aufweist. Im verbreiteten Fall flächenhaft antastender optischer Messverfahren wie der Formprüfinterferometrie, der Streifenprojektion oder der phasenmessenden Deflektometrie registrieren elektronische Kameras zunächst Bilder sinusförmiger Streifenmuster, deren geometrische Verzerrung Rückschlüsse auf die Form des Prüflings zulässt. Als eigentliche Kodierung dient dabei stets der Phasenwinkel φ innerhalb des periodischen Sinusmusters. Da jedoch die beobachtbare lokale Intensität I innerhalb des Sinusmusters gemäß Gleichung (1) nicht nur von dem gesuchten Phasenwinkel φ abhängt, sondern auch von den lokal variierenden Größen Modulation M und Hintergrundintensität I0, werden meist mehrere um jeweils definierte Phasenoffsets Δφ verschobene Muster nacheinander aufgezeichnet. Hinsichtlich der konkreten Ausgestaltung von Anzahl und Betrag der Phasenoffsets sind vielfältige Ausführungsformen bekannt, wobei zumindest auf dem Gebiet der geometrisch-optischen Messtechnik die Klasse der symmetrischen M-Schritt Algorithmen dominiert. Allen voran aufgrund seiner einfachen Implementierung der bekannte symmetrische 4-Schritt Algorithmus mit vier um jeweils 90° zueinander verschobenen Mustern.

Dieses als Phasenschiebeauswertung bezeichnete Vorgehen führt zu einer Ortskodierung in Gestalt der relativen Phase φ, deren Eindeutigkeitsbereich lediglich eine Periode des zugrundeliegenden Sinusmusters umfasst. Es kann also zunächst nicht entschieden werden, zu welcher Periode des Sinusmusters der jeweils betrachtete Bildpunkt gehört. Die Auflösung dieser Mehrdeutigkeit ist Gegenstand der sogenannten Entfaltungsverfahren, welche im Ergebnis den Übergang von der mehrdeutigen relativen Phase φ zu der innerhalb des Messbereichs eindeutigen absoluten Phase Φ bewerkstelligen.

Die bekannten Entfaltungsverfahren lassen sich in zwei grundsätzlich unterschiedliche Verfahrensklassen unterteilen, nämlich einerseits räumliche und andererseits zeitliche Ansätze. Die räumlichen Entfaltungsverfahren basieren auf der Auswertung von Nachbarschaftsbeziehungen in der zu entfaltenden relativen Phase und setzen dabei die Annahme einer zumindest abschnittsweisen Stetigkeit der kodierten Oberfläche voraus. Räumliche Entfaltungsverfahren sind insbesondere im Bereich der Formprüfinterferometrie weit verbreitet, da dort die Prüflinge meist eine global stetige Topografie aufweisen.

Die zeitlichen Entfaltungsverfahren ermöglichen hingegen eine robuste und zudem hinsichtlich der absoluten Streifenordnung eindeutige Phasenentfaltung auch an unstetigen Oberflächen, da sie prinzipbedingt für jeden einzelnen Bildpunkt – also insbesondere ohne Betrachtung seiner Nachbarschaft – die Berechnung der absoluten Phase zulassen. Allen zeitlichen Entfaltungsverfahren ist gemein, dass sie die Aufzeichnung zusätzlicher Bilder über die reine Phasenschiebesequenz hinaus erfordern und damit die für den Messvorgang benötigte Zeitdauer erhöhen. Dennoch sind insbesondere bei den auch für die Erfassung komplexer Werkstücke geeigneten Streifenprojektionssensoren die zeitlichen Entfaltungsverfahren nahezu konkurrenzlos und auch auf dem angrenzenden Gebiet der phasenmessenden Deflektometrie sind diese weit verbreitet.

Erhebliche Unterschiede zwischen den verschiedenen Ansätzen der zeitlichen Phasenentfaltung sind hinsichtlich Art und Anzahl der zusätzlich erforderlichen Muster sowie deren algorithmischer Auswertung zu verzeichnen. Das vielleicht einfachste und zumindest auf dem Gebiet der strukturierten Beleuchtung früheste Verfahren stellt die Nutzung binärer Streifenmuster in Gestalt einer Graycode-Sequenz dar [5], [6]. Als nachteilig erweist sich bei diesem Ansatz seine Fehleranfälligkeit, welche insbesondere bei Defokussierung oder schmaler werdenden Streifen stark zunimmt, da dann im Bereich der unscharf abgebildeten Kantenübergänge vermehrt Fehlentscheidungen auftreten [7].

Als leistungsfähiger erweist sich die Klasse jener zeitlicher Entfaltungsverfahren, welche auf der Kombination mehrerer Phasenschiebesequenzen unterschiedlicher Periodenlängen basieren. Durch rechnerische Bestimmung synthetischer Wellenlängen ermöglichen diese Verfahren eine vergleichsweise robuste Entfaltung und werden aufgrund der ausschließlichen Nutzung sinusförmiger Streifenmuster von Unschärfeeffekten im Bild typischerweise nur unwesentlichen beeinträchtigt. Im Wesentlichen fallen drei konkrete Ansätze in diese Verfahrensklasse: Das hierarchische Mehrfrequenzverfahren [8], das Heterodynverfahren [4] und ein zahlentheoretischer Ansatz auf Basis teilerfremder Periodenlängen [9]. Sowohl das Mehrfrequenzverfahren als auch der zahlentheoretischen Ansatz basieren auf der Auswertung von Streifenmustern mit deutlich unterschiedlicher Periodenlänge. Dabei ist eine kurze Basiswellenlänge für die Erzielung einer hohen Ortsauflösung der Phasenkodierung zuständig, während die zusätzlich erfassten, deutlich größeren Wellenlängen hauptsächlich der Entfaltung dienen. Das Heterodynverfahren basiert hingegen auf der Nutzung mehrerer, vergleichsweise dicht benachbarter Wellenlängen. Auch hierbei wird durch Berechnung synthetischer Schwebungssignale eine robuste Entfaltung der Eingangssignale ermöglicht. Zusätzlich stellt jedoch auch jedes der kurzwelligen Signale eine hochaufgelöste Ortsinformation bereit. Durch gewichtete Mittelung der typischerweise drei unabhängigen Phasensignale kann das Rauschniveau folglich ohne Mehraufwand um nahezu den Faktor 3 reduziert werden.

Der von Zuo et al. [7] für einen vereinfachten Fall angestellte direkte Vergleich der drei genannten, auf Phasensignalen unterschiedlicher Periodenlänge basierenden Entfaltungsverfahren zeigt, dass das Heterodynverfahren hinsichtlich seiner Robustheit unter ansonsten gleichen Randbedingungen den beiden anderen Verfahren etwas unterlegen ist. Aufgrund der beschriebenen Möglichkeit der Mittelung mehrere Phasensignale weist es jedoch zugleich einen besseren Informationswirkungsgrad auf, da die zusätzlichen Phasensequenzen nicht nur zur Entfaltung selbst herangezogen werden, sondern zugleich die statistische Unsicherheit der Phasenkodierung reduzieren. Das Heterodynverfahren erscheint daher trotz seiner etwas geringeren Robustheit als das für viele Anwendungsfälle vorteilhafteste Entfaltungsverfahren.

Die von Zuo et al. [7] angenommene Vereinfachung gegenüber praxisnahen Implementierungen besteht konkret in der Nutzung lediglich zweier unterschiedlicher Periodenlängen. Eine an realen Betriebsbedingungen orientierte Analyse des Entfaltungsprozesses führt jedoch zu der Feststellung, dass in der Praxis typischerweise drei unterschiedliche Wellenlängen erforderlich sind, um die gewünschten Eindeutigkeitsbereiche mit hinreichender Robustheit kodieren zu können [3], [4]. Sofern für einen konkreten Anwendungsfall die Basiswellenlänge sowie der gewünschte Eindeutigkeitsbereich definiert sind, existieren offensichtlich unterschiedlichste Kombinationen weiterer Periodenlängen, die allesamt grundsätzlich geeignet sind, eine Entfaltung der Phasensignale auszuführen. Diese Uneindeutigkeit hinsichtlich der zu kombinierenden Periodenlängen führt unweigerlich zu der Fragestellung, ob Kombinationen existieren, die sich als besonders vorteilhaft im Sinne einer optimierten Robustheit erweisen und nach welchen Kriterien sich diese vorteilhaften Kombinationen ermitteln lassen.

Für das Mehrfrequenzverfahren wurden entsprechende statistische Betrachtungen von Towers et al. [10] angestellt. Für das hier betrachtete Heterodynverfahren sind entsprechende Analysen bislang hingegen nicht bekannt. Obgleich es im Einzelfall also vergleichsweise trivial ist, grundsätzlich geeignete Wellenlängenkombinationen zu identifizieren, ist bislang nicht untersucht worden, wie stark sich unterschiedliche Wellenlängensets hinsichtlich ihrer Robustheit unterscheiden und für welche Kombination ein optimales Ergebnis zu erwarten ist. Der vorliegende Beitrag hat zum Gegenstand, diese Lücke zu schließen, indem für eine vorteilhafte, praxisnahe Implementierung des Heterodynverfahrens, mathematisch fundierte Kriterien zur Bestimmung einer optimalen Kombination von Wellenlängen formuliert werden.

3 Grundlagen des Heterodynverfahres

Bei Messverfahren, die auf der Registrierung periodischer Signale basieren, kann der Eindeutigkeitsbereich der Messung deutlich gesteigert werden, indem mehrere Signale unterschiedlicher Wellenlänge λ simultan oder sequenziell beobachtet werden. Der hierdurch nutzbare Effekt besteht in der bei Überlagerung zweier solcher Signale entstehenden Überstruktur. Dieses als Schwebung bezeichnete Signal weist eine gegenüber den Einzelsignalen erhöhte Wellenlänge Λ12 auf, welche sich aus den Wellenlängen λ1 und λ2 der Einzelsignale gemäß folgendem Zusammenhang ergibt:

Um dieses Prinzip auf das Problem der absoluten Ortskodierung mittels strukturierter Beleuchtung anzuwenden, wird die Phasenschiebeauswertung nicht nur mit einer einzelnen Sequenz von gegeneinander phasenverschobenen Sinussignalen durchgeführt, sondern es wird mindestens eine weitere Sinussequenz ausgewertet, deren Wellenlänge sich von jener der ersten geringfügig unterscheidet [4]. An beiden Musterfolgen wird zunächst unabhängig voneinander eine Phasenschiebeauswertung durchgeführt, was – wie in Abb. 1 veranschaulich – zu zwei sägezahnförmigen Phasensignalen φ1(x) und φ2(x) führt.

Die Periodenlänge dieser relativen Phaseninformation ist jeweils identisch mit jener der zugrundeliegenden Sinussignale. Durch rechnerische Überlagerung beider Signale kann daher ein ebenfalls sägezahnförmiges Schwebungssignal mit gemäß Gleichung (2) erhöhter Wellenlänge ermittelt werden. Das dafür anwendbare Auswerteverfahren wird als phasenrichtige Subtraktion bezeichnet und ist in Abb. 1 anschaulich dargestellt.

Abb. 1

Prinzip der phasenrichtigen Subtraktion.

Subtrahiert man die beiden periodischen Phasensignale mit Wellenlängen λ1 und λ2 sowie gemeinsamem Werteintervall [0,A] voneinander, so resultiert ein zunächst unstetiges Signal, mit Werten im Intervall [−A,A]. Wie an Abb. 1 nachvollziehbar, muss die resultierende Schwebung φ12(x) jedoch ebenso wie die Eingangssignale Werte im Intervall [0,A] aufweisen. Der Übergang vom reinen Differenzsignal φ1(x)−φ2(x) zum phasenrichtigen Schwebungssignal φ12(x) erfordert daher einen Entfaltungsvorgang, welcher gemäß Gleichung (3) einfach dadurch erfolgen kann, dass die Amplitude A addiert wird, sofern das reine Differenzsignal kleiner Null ist.

Theoretisch wäre die so berechnete Schwebung direkt als absolute Phasenlage eines Punktes innerhalb des Eindeutigkeitsbereichs der Länge Λ12 nutzbar. Jedoch führt die phasenrichtige Subtraktion nicht nur zu einer Vergrößerung des Eindeutigkeitsbereichs, sondern hat auch eine Erhöhung des Rauschens zur Folge. Zur Erzielung eines guten Signal-Rausch-Verhältnisses ist es daher erforderlich, unter Nutzung des im gesamten Messbereich eindeutigen Schwebungssignals φ12(x) die periodischen und damit mehrdeutigen Ursprungssignale φ1(x) und φ2(x) zu entfalten, wie im Folgenden anhand von Abb. 2 erläutert.

Abb. 2

Prinzip der Phasenentfaltung beim Heterodynverfahren.

Betrachtet man das zu entfaltende periodische Phasensignal φ(x), so sind darin in unterschiedlichen Perioden auftretende Orte gleicher relativer Phase φ1 dadurch gekennzeichnet, dass ihnen in einem als Schwebung berechneten absoluten Phasensignal Φ(x) jeweils unterschiedliche Phasenwerte zuzuordnen sind. Exemplarisch sei in Abb. 2 dem an der Position x1 zu beobachtenden Phasenwert φ1 der Wert Φ1 des Schwebungssignals zuzuordnen. Die Auswertung dieser Zuordnung gemäß nachfolgender Gleichungen (4) bis (7) ermöglicht die Bestimmung der absoluten Streifenordnung Oφ(x) innerhalb des zu entfaltenden Phasensignals φ(x). Hierzu sind zunächst das zu entfaltende Signal sowie das Schwebungssignal auf eine gemeinsame Steigung zu normieren. Mit Kenntnis der jeweiligen Steigungen gemäß Gleichungen (5) und (6) kann das absolute Phasensignal Φ(x) entsprechend Gleichung (4) in ein der Steigung von φ(x) entsprechendes Signal Φ′(x) umgerechnet werden.

mit:

Im Fall abweichungsfreier Eingangssignale enthielte die so ermittelte Ordnungsfunktion Oφ(x) nur Werte aus der Menge der natürlichen Zahlen. Aufgrund des Rauschens realer Phasenmessungen sind die gemäß Gleichung (7) berechneten Funktionswerte in der Praxis jedoch zunächst auf ganze Zahlen zu runden, ehe schließlich das periodische Phasensignal φ(x) durch Summenbildung gemäß Gleichung (8) in ein absolutes, entfaltetes Phasensignal φabs(x) überführt werden kann.

Da wie erwähnt Abweichungen der Eingangssignale φ(x) und Φ(x) zu Abweichungen der Ordnungsfunktion Oφ(x) führen, besteht grundsätzlich die Möglichkeit, dass eine fehlerhafte Ordnungsbestimmung erfolgt. Ausgehend von Gleichung (7) tritt eine Fehlbestimmung der Ordnung dann auf, wenn die Abweichungen ΔΦ′(x) und Δφ(x) die Bedingung aus Gleichung (9) erfüllen.

Für die korrekte Interpretation von Gleichung (9) sowie noch folgender Ausführungen in Abschnitt 5 ist an dieser Stelle hervorzuheben, dass es sich bei den mit der Voranstellung Δ gekennzeichneten Quantitäten nicht um statistische Unsicherheiten handelt und somit Gleichung (9) nicht als der Versuch einer klassischen Abweichungsfortpflanzung zu verstehen ist. Vielmehr wird hier für konkrete Einzelmesswerte eine Zerlegung in den richtigen Wert und in einen vorzeichenbehafteten Abweichungsanteil vorgenommen. In diesem Sinne kennzeichnet etwa der Ausdruck Δφ(x) in Gleichung (9) in allgemeiner Form die Abweichung eines einzelnen Messwertes von seinem richtigen Wert φ(x).

In Abb. 2 ist, bezogen auf die nicht normierten Signale, die Schwelle aus Gleichung (9) als maximal zulässigen Abweichung Emax eingetragen. Da das Phasensignal Φ′(x) nach Gleichung (4) aus einer Skalierung von Φ(x) mit dem Verhältnis der Periodenlängen λΦ und λφ hervorgeht, werden die Phasenabweichungen von Φ(x) ebenfalls um den Faktor λΦ/λφ verstärkt. Bei gegebenem Signal-Rausch-Verhältnis sind daher dem zuverlässig auswertbaren Wellenlängenverhältnis λΦ/λφ Grenzen gesetzt.

Im Hinblick auf eine absolute Ortskodierung unter Einsatz einer möglichst kurzen Mustersequenz wäre es wünschenswert, die Sinuswellenlängen λ1 und λ2 so zu wählen, dass die Wellenlänge Λ12 der resultierenden Schwebung den gesamten Messbereich umfasst. Zugleich sollten die Wellenlängen λ1 und λ2 klein genug sein, um eine hinreichende Ortsauflösung erreichen zu können. Wie in [3] gezeigt, ist für hinsichtlich Wellenlänge, Eindeutigkeitsbereich und Signal-Rausch-Verhältnis typische Szenarien durch Einsatz nur zweier Wellenlängen λ1 und λ2 keine robuste Entfaltung realisierbar.

Bei Kombination von insgesamt drei Sinussignalen unterschiedlicher Wellenlänge kann hingegen unter gängigen Randbedingungen eine korrekte Entfaltung erreicht werden, wenn die Entfaltung in mehreren Schritten vorgenommen wird. Es wird daher für nachfolgende Betrachtungen der Einsatz dreier Wellenlängen λ0.1, λ0.2 und λ0.3 zugrunde gelegt, wobei gilt:

Durch das beschriebene Verfahren der phasenrichtigen Subtraktion werden somit – wie in Abb. 3 veranschaulicht – zunächst aus den durch Phasenschiebeauswertung direkt gewonnenen Signalen zu den Wellenlängen λ0.1, λ0.2 und λ0.3 die Schwebungssignale der ersten Stufe mit den Wellenlängen λ1.1 und λ1.2 berechnet. Aus diesen wird in der Folge das Schwebungssignal der zweiten Stufe mit der Wellenlänge λ2.1 ermittelt.

Abb. 3

Prinzip der sequenziellen Berechnung der Schwebungssignale aus den Eingangssignalen.

Abb. 4

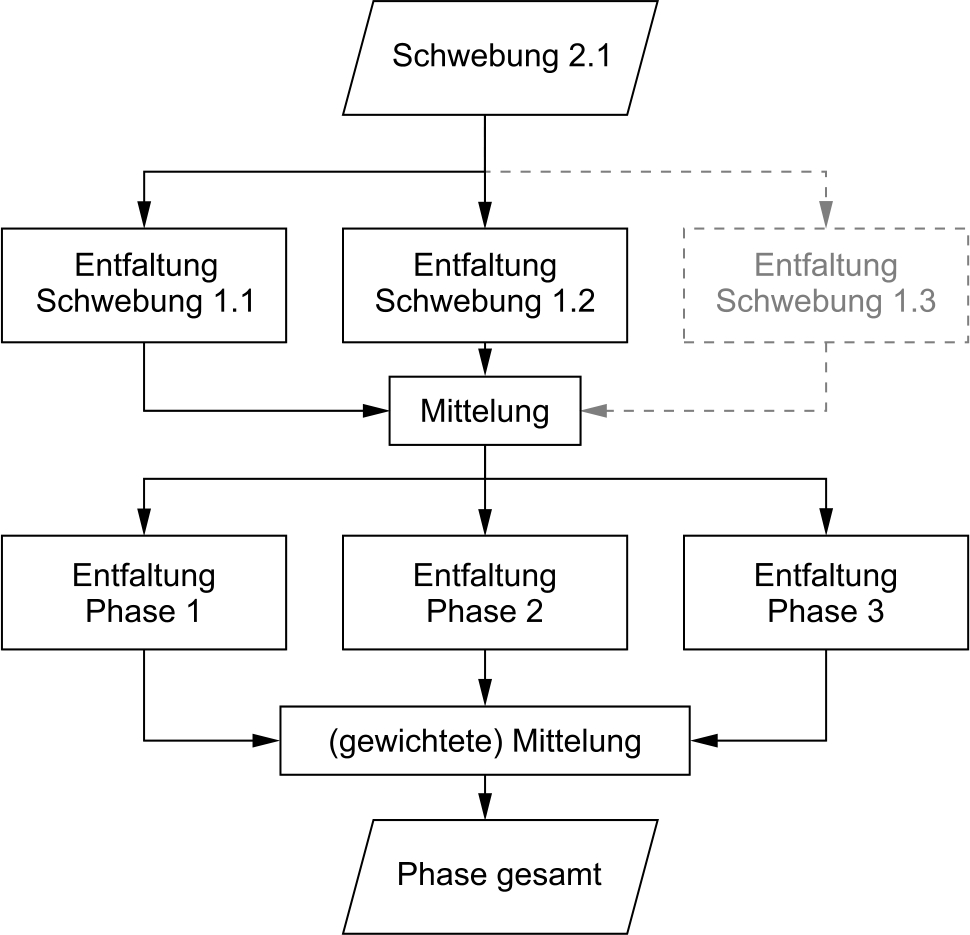
Prinzip der hierarchischen Entfaltung der Schwebungssignale sowie der Eingangssignale.

Abb. 5

Exemplarische Simulation der Phasenfehler in einem Bild von 2000×1500px2, verursacht durch Fehlentscheidungen im Entfaltungsprozess.

Die so erzeugten langwelligen Schwebungssignale der ersten und zweiten Stufe werden im Weiteren für die hierarchische Entfaltung der jeweils vorangegangenen Stufe genutzt. Wie in Abb. 4 dargestellt, werden mittels der im gesamten Auswertebereich eindeutigen Schwebung der zweiten Stufe die Schwebungssignale der ersten Stufe entfaltet. Diese entfalteten Schwebungssignale der ersten Stufe werden beispielsweise durch Mittelwertbildung miteinander fusioniert und das so resultierende Signal kann schließlich zur Entfaltung der drei Eingangssignale genutzt werden, deren – gegebenenfalls gewichteter – Mittelwert das finale Ergebnis der Phasenmessung darstellt.

4 Entfaltungsfehler

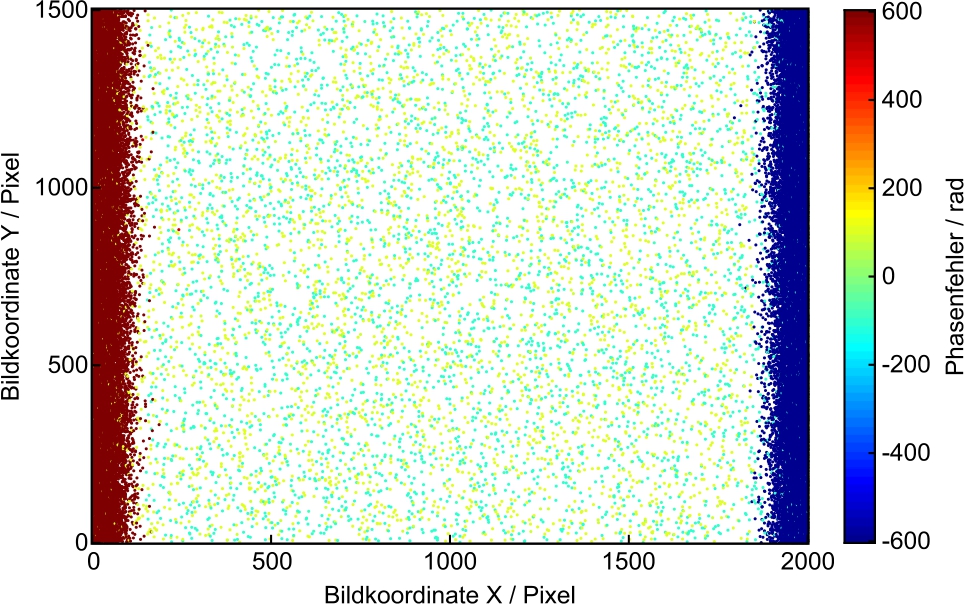
Um die bei der Entfaltung auftretenden Fehlentscheidungen zu veranschaulichen, ist in Abb. 5 das Ergebnis einer simulierten horizontalen Phasenkodierung gemäß des in Abschnitt 3 beschriebenen Berechnungsverfahren in einem virtuellen Bildbereich von 2000×1500px2 dargestellt. Die drei Wellenlängen λ0.1≈20px, λ0.2≈21,581px und λ0.3≈23,162px sind dabei so bestimmt, dass der Eindeutigkeitsbereich mit 2000px gerade der Bildfeldbreite entspricht. Das normalverteilte Phasenrauschen der Eingangssignale wurde mit einer Standardabweichung von σ=π/50 (entsprechend einem relativen Phasenfehler von 1/100) größer als bei einer typischen Messung gewählt, so dass eine erhebliche Anzahl von Fehlstellen auftritt. In Abb. 5 sind nur diese Fehlstellen eingetragen, also solche Punkte, an denen infolge von Entfaltungsfehlern große Abweichungen der entfalteten Phasenwerte auftreten. Darüber hinaus weist natürlich eine rauschbehaftete Phasenmessung in jedem Bildpunkt statistische Abweichungen von der idealen Phase auf, welche im Rahmen dieses Beitrags jedoch erst in Abschnitt 6 näher betrachtet werden. Zunächst werden nur die im Vergleich mit den statistischen Abweichungen großen Phasenfehler infolge von Fehlentscheidungen im Entfaltungsprozess betrachtet.

Wie aus Abb. 5 zu ersehen, sind offensichtlich unterschiedliche Typen von Entfaltungsfehlern zu verzeichnen. Am auffälligsten sind zunächst die Zonen entlang des linken und rechten Randes des Auswertebereichs, in welchen eine sehr hohe Anzahl von Fehlstellen mit betragsmäßig sehr großer Amplitude festzustellen ist. Diese Fehlstellen – im Folgenden als Fehlertyp 1 bezeichnet – resultieren aus der Berechnung der zweiten Schwebungsstufe mittels phasenrichtiger Subtraktion und treten prinzipbedingt in der Umgebung der Unstetigkeitsstelle der Phasenfunktion, hier also an den Enden des Eindeutigkeitsbereichs, auf [7]. Darüber hinaus sind Fehlstellen zu erkennen, die gleichmäßig im gesamten Auswertebereich verteilt sind und deutlich geringere betragsmäßige Amplituden aufweisen. Diese im Weiteren als Fehlertyp 2 bezeichneten Fehlstellen resultieren aus der Entfaltung der Signale der ersten Schwebungsstufe sowie der Entfaltung der Eingangssignale. Ihre Amplitude hängt zum einen davon ab, in welcher Entfaltungsstufe die zugehörige Fehlentscheidung aufgetreten ist und ob gegebenenfalls mehrere Fehlentscheidungen gleichzeitig – in derselben oder auch in unterschiedlichen Entfaltungsstufen – aufgetreten sind. Die statistische Analyse des Entfaltungsvorgangs im Hinblick auf die Entstehung der gezeigten Entfaltungsfehler, sowie die Formulierung von Kriterien zur Minimierung der Auftretenswahrscheinlichkeiten derselben sind Gegenstand des nachfolgenden Abschnitts 5.

5 Statistische Analyse des Entfaltungsvorgangs

Ausgehend von den vorangegangenen Beschreibungen des Entfaltungsprozesses mittels Heterodynverfahren sowie den aufgezeigten Fehlertypen wird im Folgenden eine detaillierte statistische Analyse des gesamten Auswertevorgangs durchgeführt, beginnend mit den drei rauschbehafteten Eingangsphasen φ0.1, φ0.2 und φ0.3 über die Schwebungsstufen 1 und 2 sowie die anschließende Entfaltung der Signale der Schwebungsstufe 1 und schließlich der Eingangsphasen. Zunächst stehen dabei die Entstehung von Fehlertyp 2 (vergleiche Abschnitt 4) sowie die Minimierung der Wahrscheinlichkeit für ein Auftreten desselben im Vordergrund. Im Anschluss werden Aussagen zur Auftretenswahrscheinlichkeit und zur Vermeidung des Fehlertyps 1 getroffen.

Die Schwebungssignale 1.1, 1.2 und 2.1 entstehen durch phasenrichtige Subtraktion aus den Eingangsphasen φ0.1, φ0.2 und φ0.3 wie folgt:

Die Ordnungsfunktion Oφ1.1 zur Entfaltung des ersten Schwebungssignals der ersten Stufe φ1.1 unter Berücksichtigung des Schwebungssignals der zweiten Stufe φ2.1 ergibt sich gemäß Gleichungen (4) und (7) sowie mit Gleichungen (11), (13) und (14) zu:

Für das zweite Schwebungssignal der ersten Stufe φ1.2 folgt analog zu Gleichung (15):

Für die Abweichungen von Oφ1.1 und Oφ1.2 aufgrund der statistischen Abweichungen der Phasenwerte gilt ausgehend von Gleichungen (15) und (16) damit:

Da zur Entfaltung der Signale die Ordnungsfunktion mathematisch auf die nächstliegende ganze Zahl gerundet wird, muss zur Vermeidung einer Fehlbestimmung der Ordnung allgemein gelten:

Zur sich anschließenden Entfaltung der Eingangssignale φ0.1, φ0.2 und φ0.3 wird der arithmetische Mittelwert Φ1.avg der bereits entfalteten Schwebungssignale Φ1.1 und Φ1.2 herangezogen, für die jeweils gilt:

Der Mittelwert der mit Hilfe des Wellenlängenverhältnisses aufeinander skalierten Schwebungssignale beträgt damit:

Da das Produkt aus ganzzahliger, gerundeter Streifenordnung und konstanter Amplitude A in den entfalteten absoluten Phasen Φ1.1 und Φ1.2 gemäß Gleichungen (20) und (21) keinen Beitrag zur statistischen Abweichung des Schwebungssignals liefert, sind nur die darin enthaltenen relativen Phasenanteile φ1.1 und φ1.2 entscheidend für die weitere Unsicherheitsbetrachtung. Deren Mittelwert kann ausgehend von Gleichung (22) unter Hinzuziehung der Gleichungen (20) und (21) wie folgt auf die Eingangssignale φ0.1, φ0.2 und φ0.3 zurückgeführt werden:

Die Ordnungsfunktion zur Entfaltung des Phasensignals φ0.1, wiederum mit normierten Eingangsphasen, ergibt sich zu:

Da wie ausgeführt die in Φn1.avg enthaltenen Beiträge der Ordnungsfunktionen nicht zur statistischen Unsicherheit von (24) beitragen, kann die Abweichung von Oφ0.1 ausgehend von Gleichung (23) wie folgt notiert werden:

Mit analoger Herleitung ergibt sich für die Abweichungen der Ordnungsfunktionen Oφ0.2 und Oφ0.3:

Maßgeblich für das Auftreten von Entfaltungsfehlern sind letztlich jedoch nicht direkt die Korrelationen auf Ebene der Abweichungen der Ordnungsfunktionen, sondern jene auf Ebene der Fehlentscheidungen, also der Verletzung der Bedingung aus Gleichung (19). Es müssen also im Weiteren daher jene Signale betrachtet werden, die aus den Abweichungen der Ordnungsfunktionen durch die Auswertung der Bedingung für eine Fehlentscheidung hervorgehen. Diese Funktion kann geschrieben werden als:

Auf Ebene dieser Fehlerfunktion E für die einzelnen Entfaltungsvorgänge zeigt sich, dass nahezu alle in den Signalen Φ0.2 und Φ0.3 auftretenden Fehler auch in Φ0.1 enthalten sind. Ebenso sind nahezu alle in Φ1.2 enthaltenen Fehler bereits in Φ1.1 enthalten. Zwischen den beiden Entfaltungsstufen besteht für niedrige Fehlerwahrscheinlichkeiten hingegen quasi keinerlei Überdeckung der Fehlstellen. Die Koinzidenzmatrix in Tab. 2 gibt die Zusammenhänge für die Tab. 1 zugrunde liegenden Daten quantitativ wieder. Die Einträge in den Zeilen sind dabei als die vorhersagende Größe zu verstehen, während die Einträge in den Spalten die vorhergesagten Größen darstellen.

Tab. 2

Koinzidenzmatrix der Fehlentscheidungen bei Auswertung der Ordnungsfunktionen, ermittelt mit Parametern wie in Tab. 1. Ablesebeispiel: Von den in Eφ0.2 enthaltenen Fehlstellen sind 93,95 % auch in Eφ0.1 enthalten. Umgekehrt sind jedoch nur 75,09 % der in Eφ0.1 auftretenden Fehlstellen in Eφ0.2 enthalten.

		vorhergesagte Größe
		Eφ0.1	Eφ0.2	Eφ0.3	Eφ1.1	Eφ1.2
	Eφ0.1	1	0,9395	0,9925	0,0109	0,0048
	Eφ0.2	0,7509	1	0,7931	0,004	0,0018
	Eφ0.3	0,9486	0,9484	1	0,0093	0,004
	Eφ1.1	0,0109	0,0051	0,0097	1	0,9688
	Eφ1.2	0,0025	0,0012	0,0021	0,5022	1

Aufgrund dieser Korrelationen entspricht die Fehlerrate in einer Entfaltungsstufe in sehr guter Näherung der maximalen Einzelwahrscheinlichkeit in dieser Stufe, da aufgrund des binären Entscheidungscharakters sich die Fehlerraten bei Korrelation gerade nicht addieren. Es können daher die Abweichungen ΔOφ0.1 und ΔOφ1.1, die aufgrund der Forderung aus Gleichung (10) die jeweiligen Maximalwerte innerhalb ihrer Entfaltungsstufen darstellen, herangezogen werden um die Gesamtfehlerwahrscheinlichkeit zu berechnen. Um im Weiteren statistisch optimale Werte für die drei Basiswellenlängen λ0.1, λ0.2 und λ0.3 ermitteln zu können, werden ausgehend von den Gleichungen (17) und (25) zunächst die statistischen Unsicherheiten uOφ0.1 und uOφ1.1 formuliert. Da die Wellenlängen λ0.1, λ0.2 und λ0.3 nahe beieinander liegen, sind die resultierenden relativen Unsicherheiten der drei zugehörigen Phasensignale typischerweise in guter Näherung gleich groß, so dass folgende vereinfachende Annahme zweckmäßig und gerechtfertigt erscheint:

Unter Annahme von (29) kann für die maßgeblichen Unsicherheiten der Ordnungsfunktionen Oφ0.1 und Oφ1.1 daher geschrieben werden:

Hierin steht P für die Summenfunktion der Standardisierten Normalverteilung. Als relevante Unsicherheiten uOφi.j werden hier wie oben ausgeführt die jeweiligen Unsicherheiten uOφ0.1 sowie uOφ1.1 angesetzt. Der Vorfaktor 2 ist zu berücksichtigen, da die Fehlentscheidung entsprechend der Betragsstriche in Gleichung (19) mit derselben Wahrscheinlichkeit nach oben und nach unter erfolgen kann.

Die Fehlentscheidungen in den Stufen 0 und 1 entsprechen jeweils einer Binomialverteilung mit den Einzelwahrscheinlichkeiten p0.1 und p1.1. Die Kombination pges dieser beiden Einzelwahrscheinlichkeiten ergibt sich zu:

Der subtraktive Anteil p0.1·p1.1 tritt auf, da mit zunehmenden Einzelwahrscheinlichkeiten Entfaltungsfehler in beiden Stufen an denselben Stellen auftreten. Somit verringert sich die Gesamtfehlerzahl, da ein in beiden Stufen an derselben Stelle auftretender Fehler sich aufgrund des binären Entscheidungscharakters nur als ein Fehler auswirkt.

Wenn die Basiswellenlänge λ0.1 sowie der hier mit R bezeichnete Eindeutigkeitsbereich gewählt und die Unsicherheiten uφn0.j – oder mit Gleichung (29) vereinfachend uφn – der Phasensignale bekannt sind, können die statistisch optimalen Wellenlängen λ0.2 und λ0.3 durch Lösung des folgenden Optimierungsproblems ermittelt werden.

Dabei sind als zusätzliche Nebenbedingungen anzusetzen:

Da das vorgenannte Optimierungsproblem sich in der Umsetzung als vergleichsweise anspruchsvoll erweist und zudem die Unsicherheit uφn der Phasensignale infolge der Beleuchtungsverhältnisse ohnehin innerhalb des Bildfeldes lokal variiert, wird im Weiteren ein Näherungskriterium abgeleitet, welches unter praxisrelevanten Randbedingungen vergleichbare Ergebnisse liefert.

So konnte beobachtet werden, dass für kleine Phasenunsicherheiten – und damit kleine Fehlerraten – die optimale Lösung gemäß Gleichung (34) zugleich dadurch gekennzeichnet ist, dass gilt:

Für größere Fehlerraten kann die optimale Lösung gemäß Gleichung (34) zwar zu einem hiervon abweichenden Verhältnis von uOφ0.1 und uOφ1.1 führen, jedoch erscheinen Fälle mit großer Fehlerrate nicht praxisrelevant, da sie keinen zuverlässigen Messprozess ermöglichen. Für anwendungsrelevante Fälle mit Fehlerraten unter 1 % liegen die optimale Lösung nach Gleichung (34) sowie die Näherungslösung nach Gleichung (37) so nahe beieinander, dass eine Unterscheidung nicht zweckmäßig erscheint. Die direkt auf Ebene der Empfindlichkeitskoeffizienten in Gleichungen (30) und (31) anwendbare Optimierung erscheint daher als die vorteilhaftere Variante. Dies gilt auch für den Fall unterschiedlicher Unsicherheiten von φ0.1, φ0.2 und φ0.3, also wenn die Annahme gemäß Gleichung (29) nicht gilt.

Unter Annahme der Gültigkeit von Gleichung (29) sind die Wellenlängen λ0.1, λ0.2 und λ0.3 also so zu wählen, dass folgende, aus den Gleichungen (30) und (31) abgeleitete Bedingung gilt:

Auch hierbei sind wiederum die Nebenbedingungen gemäß Gleichungen (35) und (36) zu berücksichtigen.

Um die Auswirkungen eines gemäß Gleichungen (34) oder (38) optimierten Wellenlängenverhältnisses aufzuzeigen, wurden Monte-Carlo-Simulationen durchgeführt, in deren Zuge die Fehlerwahrscheinlichkeit in Abhängigkeit des relativen Phasenrauschens der Eingangssignale für unterschiedliche Wellenlängenverhältnisse verglichen wurde. Hierzu wurden zwei einfache, aber naheliegende Alternativansätze zur Bestimmung der Wellenlängen λ0.2 und λ0.3 bei gegebener Basiswellenlänge λ0.1 und jeweils der Berücksichtigung der Nebenbedingungen gemäß Gleichungen (35) und (36) betrachtet. Dies sind erstens ein im Folgenden als „äquidistant“ bezeichneter Ansatz mit konstantem Inkrement Iλ, so dass gilt λ0.2=λ0.1+Iλ und λ0.3=λ0.1+2·Iλ sowie zweitens ein im Folgenden als „äquifaktoriell“ bezeichneter Ansatz mit konstantem Faktor Fλ, so dass gilt λ0.2=Fλ·λ0.1 und λ0.3=Fλ2·λ0.1. In Abb. 6 sind für eine Basiswellenlänge von λ0.1=20px und einen Eindeutigkeitsbereich von R=2000px die Wahrscheinlichkeiten für Entfaltungsfehler vom Typ 2 in Abhängigkeit des relativen Phasenrauschens der Eingangssignale gegenübergestellt, wobei die optimierten Wellenlängen mittels des Näherungskriteriums gemäß Gleichung (38) ermittelt wurden. Die Gegenüberstellung zeigt, dass sich trotz der ähnlichen Wellenlängen hinsichtlich der erzielbaren Fehlerwahrscheinlichkeiten Unterschiede von mehreren Größenordnungen einstellen. Bemerkenswert ist zudem, dass die relative Verbesserung durch Nutzung eines optimierten Ansatzes mit geringer werdendem Rauschen der Eingangssignale sogar deutlich zunimmt. Um die Absolutwerte der Fehlerwahrscheinlichkeiten angemessen zu interpretieren, ist zudem zu bedenken, dass bei Nutzung hochauflösender elektronischer Kameras in der Regel mehrere Millionen Pixel pro Einzelmessung kodiert werden.

Abb. 6

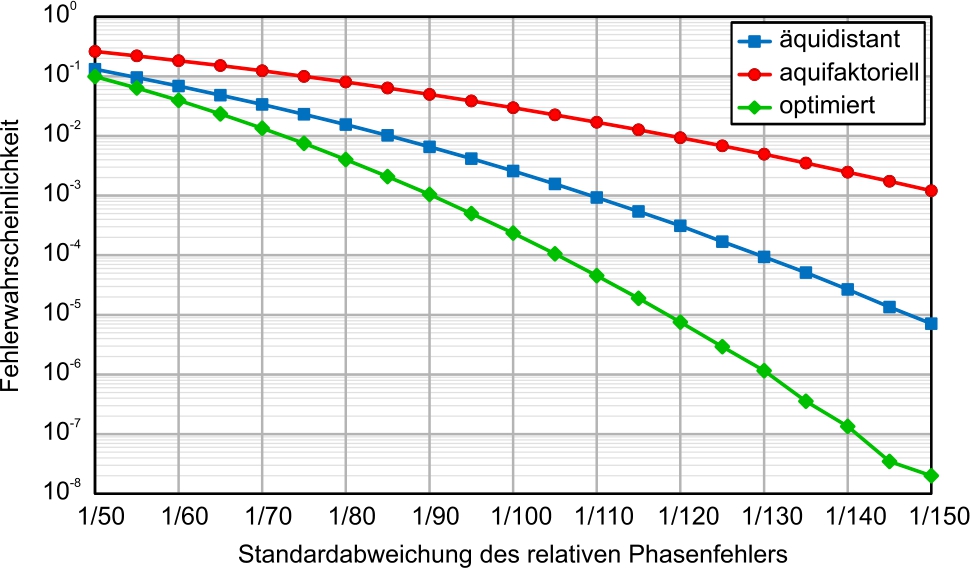
Erhöhung der Robustheit durch Optimierung des Wellenlängenverhältnisses, hier Ergebnisse einer Monte-Carlo-Simulation. Alle drei Wellenlängensets weisen eine Basiswellenlänge von λ0.1=20px auf und ermöglichen einen Eindeutigkeitsbereich von 2000px. Im Modus „äquidistant“ gilt λ0.2≈21,5809px und λ0.3≈23,1618px; im Modus „äquifaktoriell“ gilt λ0.2≈22,2222px und λ0.3≈24,6914px; im Modus „optimiert“ gilt λ0.2≈21,2327px und λ0.3≈22,3742px.

Ausgehend von den oben angestellten statistischen Betrachtungen des Entfaltungsvorgangs können neben den formulierten Optimalitätskriterien gemäß Gleichungen (34) und (38) weitere nutzbringende Schlussfolgerungen bezüglich der vorteilhaften Ausgestaltung des Entfaltungsvorgangs abgeleitet werden. So zeigen die beobachteten hohen Korrelationen innerhalb der einzelnen Stufen (vgl. Tab. 2) auf, weshalb der naheliegende Versuch einer Fehlerkorrektur durch Vergleich der vermeintlich redundanten entfalteten Phasensignale Φ0.1, Φ0.2 und Φ0.3 nahezu keinerlei Nutzen hat. Falls nämlich Entfaltungsfehler auftreten, dann treten sie mit hoher Wahrscheinlichkeit in mehr als nur einem der drei Signale auf. Entsprechende algorithmische Korrekturversuche sind somit zwar theoretisch vorteilhaft, führen praktisch jedoch nur zu einer marginalen Reduzierung der Fehlerrate. Im Interesse einer Minimierung der benötigten Rechenzeit kann auf diesen Korrekturschritt daher gut verzichtet werden.

Eine ähnliche Schlussfolgerung ist im Hinblick auf die Signale der ersten Schwebungsstufe möglich. In [3] wurde noch nahegelegt, zusätzlich zu den Schwebungssignalen φ1.1 und φ1.2 auch das dritte Schwebungssignal φ1.3 zu berechnen (vgl. Abb. 3 und Abb. 4) und zur Fehlererkennung und -korrektur einzusetzen. Dieses Vorgehen kann auf Grundlage der hier vorgenommenen Untersuchungen nicht mehr als zielführend empfohlen werden. Aufgrund der vergleichsweise kurzen Wellenlänge des Schwebungssignals φ1.3 und des damit in Relation zum Schwebungssignal der zweiten Stufe φ2.1 größeren Wellenlängenverhältnis ergibt sich für die Entfaltung von φ1.3 eine deutlich höhere Empfindlichkeit gegenüber den Unsicherheiten der Eingangssignale. Dies hat zur Folge, dass durch Berücksichtigung des entsprechenden entfalteten Signals Φ1.3 eine hohe Zahl von Fehlstellen eingebracht wird, welche in der Folge auf Grundlage der im Vergleich deutlich robusteren Signale Φ1.1 und Φ1.2 korrigiert werden müssen. Der umgekehrte Fall, dass ein Fehler nur in Φ1.1 oder Φ1.2 auftritt und mit Hilfe von Φ1.3 erfolgreich korrigiert werden kann, tritt aufgrund der hohen Korrelation zwischen Φ1.1 und Φ1.2 sowie der geringen Robustheit von Φ1.3 quasi nicht auf, weswegen der zusätzliche Rechenaufwand vermieden werden sollte.

Für ein besseres Verständnis des in Abschnitt 4 aufgezeigten Fehlertyps 1 entlang der Ränder des Kodierungsbereichs sind die allgemeine Gleichung (3) sowie die für die Schwebung der zweiten Stufe gültige Gleichung (13) heranzuziehen. Da das aus der Subtraktion resultierende Rohsignal gemäß Gleichung (3) erforderlichenfalls durch Addition der Amplitude von A=2π in das Intervall [0,2π] überführt wird, kommt es bedingt durch das überlagerte Rauschen zu Fehlern bei der Entscheidung, ob diese Addition überhaupt erforderlich ist. Problematisch ist diese Entscheidung in jenen Zonen des Auswertebereichs, in welchen die tatsächliche Phase in der Nähe von Null oder 2π liegt, was gerade in den Randbereichen der Fall ist. So kommt es wie in Abb. 7 veranschaulicht am linken Rand zu einer fehlerhaften Addition von A, sofern das Differenzsignal infolge des Rauschens den Wert Null unterschreitet. Am rechten Rand, an welchem die tatsächliche Phase gegen 2π strebt, wird unter Umständen fälschlich A nicht addiert, da das Differenzsignal rauschbedingt gerade oberhalb von Null liegt.

Abb. 7

Exemplarisches Ergebnis der phasenrichtigen Subtraktion entlang einer Zeile des Auswertebereichs mit rauschbedingten Fehlentscheidungen.

Der Fehler vom Typ 1 beträgt auf Ebene des Schwebungssignals folglich stets 2π. Im resultierenden Gesamtergebnis wird dieser Fehler noch um das Wellenlängenverhältnis λ2.1/λ0.1 hochskaliert und beträgt daher unter den hier betrachteten Randbedingungen wie in Abb. 5 dargestellt 200π. In den meisten phasenmessenden Systemen wie den photogrammetrischen Streifenprojektionssensoren oder auch der phasenmessenden Deflektometrie stehen Vorkenntnisse hinsichtlich der Systemgeometrie zur Verfügung, die genutzt werden können, um diese Fehlstellen zu identifizieren und rechnerisch zu korrigieren. Soll das Auftreten von Fehlern dieses Typs hingegen vermieden werden, so ist dies nur möglich, wenn die entsprechenden Randbereiche bei der Phasenkodierung ungenutzt bleiben. In diesem Fall wäre also der Eindeutigkeitsbereich R des Hetereodynverfahrens größer zu wählen, als der tatsächlich benötigte Kodierungsbereich und die Streifenmuster wären auf dem Projektor oder Bildschirm so darzustellen, dass die entsprechenden Überlappbereiche an beiden Rändern nicht zur Anzeige kommen.

Die Abschätzung des abhängig vom vorhandenen Rauschniveau der Eingangsphasen zu verwendenden Überlappbereichs kann durch eine statistische Betrachtung ausgehend von Gleichung (13) erfolgen. Unter der Annahme gleicher relativer Unsicherheiten der drei Eingangsphasen φn0.1, φn0.2 und φn0.3 gemäß Gleichung (29) gilt für die Unsicherheit von φn2.1:

Für die Bestimmung des benötigten Überlappbereichs muss die Unsicherheit gemäß Gleichung (39) in Verhältnis zur Steigung des Phasensignals φn2.1 gesetzt werden, welche aufgrund der Normierung 1/λ2.1 beträgt. Zur Festlegung der Wahrscheinlichkeit des Auftretens von Fehlentscheidungen des Typs 1 ist ein geeigneter Erweiterungsfaktor k zu berücksichtigen. Zweckmäßigerweise erfolgt zudem die Angabe des Überlapps nicht in Pixel, sondern in Vielfachen der Basiswellenlänge λ0.1, so dass der auf beiden Seiten des Auswertebereich zu berücksichtigende, auf die Basiswellenlänge bezogene Überlapp Lλ wie folgt bestimmt werden kann:

Bei gegebener Schwebungswellenlänge λ2.1 betrüge der effektiv nutzbare Messbereich M somit:

Für den oben exemplarisch betrachteten Fall einer Schwebungswellenlänge von λ2.1=2000px wäre bei einem relativen Phasenrauschen mit einer Standardunsicherheit von 1/400 und einem Erweiterungsfaktor von k=3 demnach ein Messbereich von ungefähr 1926,5px nutzbar, was zur Kodierung der Breite eines Full-HD-Displays oder -Projektors ausreichend wäre. Bei Eingangssignalen mit deutlich größeren Unsicherheiten können die erforderlichen Überlappbereiche für eine hinreichend sichere Vermeidung von Fehlstellen hingegen vergleichsweise große Werte annehmen, so dass in diesen Fällen die rechnerische Korrektur der Fehlstellen unter Einbeziehung von Vorkenntnissen die attraktivere Vorgehensweise sein kann.

6 Minimierung der statistischen Unsicherheit der Ortskodierung

Sowohl bei der Streifenprojektion – bei welcher das zur Kodierung verwendete Streifenmuster auf das Objekt projiziert und diffus zurückgestreut wird – als auch bei der Deflektometrie – bei welcher das Streifenmuster am Prüfling reflektiert wird – hängt das von der Kamera registrierte Erscheinungsbild der Streifenmuster in hohem Maße von der Geometrie und den Rückstreueigenschaften der zu erfassenden Oberfläche ab. Insbesondere hat eine Verringerung des wahrnehmbaren Streifenkontrasts eine Erhöhung der statistischen Unsicherheit bei der Auswertung von Phasenschiebesequenzen zur Folge. In einer konkreten Messsituation stellt sich daher die Frage, bei welcher Streifenperiode die statistisch besten Ergebnisse der Ortskodierung erzielt werden können.

Für die Bestimmung der Unsicherheit der Ortskodierung sind zum einen die Unsicherheiten der Phasenmessung selbst und zum anderen die als Bezugslänge wirkende Streifenperiode maßgeblich. Zur Vorhersage des Phasenrauschens kommt nachfolgend das von Fischer et al. [11], [12] formulierte und verifizierte Phasenrauschmodell zur Anwendung, welches auf dem linearen Kamerarauschmodell der EMVA 1288 [13] aufsetzt. Hierin wird die im Verlauf einer Phasenschiebesequenz in einem Pixel beobachtbare Intensität Ii gemäß Gleichung (42) ausgedrückt.

Dabei ist φ der zu bestimmende Phasenwinkel, ψi die wählbare Phasenverschiebung des entsprechenden Musters und M die Gesamtanzahl der verwendeten Muster. Der als Belichtung bezeichnete Parameter β sowie der als Sichtbarkeit bezeichnete Parameter γ kennzeichnen die Beleuchtungs- und Kontrastverhältnisse in normierten Koordinaten, so dass die Sättigungskapazität Isat als einzige kameraspezifische Kenngröße verbleibt. Das Streifenmuster im Hintergrund der Abb. 9 stellt eine Visualisierung des durch die Größen β und γ aufgespannten Parameterraums dar.

Zur Vorhersage des absoluten Phasenrauschens formuliert Fischer einen Ausdruck, welcher ausschließlich von EMVA-konformen Kamerakenngrößen sowie den während einer Phasenschiebesequenz registrierten Intensitäten abhängt. Für den hier angenommenen Sonderfall eines symmetrischen 4-Schritt Phasenschiebealgorithmus ergibt sich der Schätzwert des Phasenrauschens zu:

Bei dem darin enthaltenen Faktor K handelt es sich um die Systemverstärkung der Kamera gemäß EMVA 1288. Die Parameter σd und μd stehen für die Standardabweichung und den Erwartungswert des Dunkelrauschens, gemäß EMVA 1288 jeweils in der Einheit e−. Diese Kennwerte können entweder direkt einem EMVA-konformen Datenblatt des Kameraherstellers entnommen oder wie in der EMVA 1288 beschrieben vom Anwender experimentell ermittelt werden. Die Intensitäten y1 bis y4 gehen aus den von der Kamera registrierten Intensitäten Ii hervor, indem erforderlichenfalls der Erwartungswert des Dunkelrauschens μy.dark (hier in digitalen Grauwerten) subtrahiert wird. Da die meisten elektronischen Kameras heute über eine automatische Dunkelrauschkorrektur verfügen, kann dieser Schritt jedoch meist übersprungen werden.

Um die so ermittelte Standardabweichung des absoluten Phasenrauschens in eine geometrische Länge zu überführen, ist die Wellenlänge im Ort mit heranzuziehen. Hierzu wird gemäß Gleichung (44) durch Normierung auf die Periode von 2π die Abweichung der absoluten Phase in eine relative Phasenabweichung umgerechnet und mit der räumlich verkörperten Periodenlänge λ gewichtet.

In Abb. 8 ist exemplarisch das Resultat einer experimentellen Bestimmung der statistisch optimalen Streifenbreite dargestellt, wobei hier eine Kamera direkt auf einen Flüssigkristallbildschirm blickt, welcher mit den Streifenmustern einer symmetrischen 4-Schritt Phasensequenz beaufschlagt wird. Als geometrische Bezugslänge wird dabei die Streifenperiode in der Einheit Bildschirmpixel angesetzt. Mit dem bekannten Pixelpitch wäre jedoch auch die direkte Angabe einer metrischen Länge möglich.

Es ist zu erkennen, dass die Phasenabweichung ausgehend von der kürzesten Wellenlänge von hier 9 Pixel zu größeren Wellenlänge hin rasch abfällt, wobei die Kurve im weiteren Verlauf stark abflacht, so dass jenseits von 25 Pixel kaum mehr eine Reduzierung des Phasenrauschens zu verzeichnen ist. Dies kann so interpretiert werden kann, dass der Streifenkontrast ab dort nahezu vollständig ausgeprägt ist. Die unter Berücksichtigung der jeweiligen Wellenlänge ermittelte Positionsabweichung hingegen fällt zu Beginn ebenso deutlich ab, erreicht dann jedoch rasch ein Minimum und steigt hin zu größeren Wellenlängen wieder an. Die minimale Abweichung der Ortskodierung ergibt sich in dieser konkreten Messanordnung demnach für eine Wellenlänge von etwa 17 Pixel.

Abb. 8

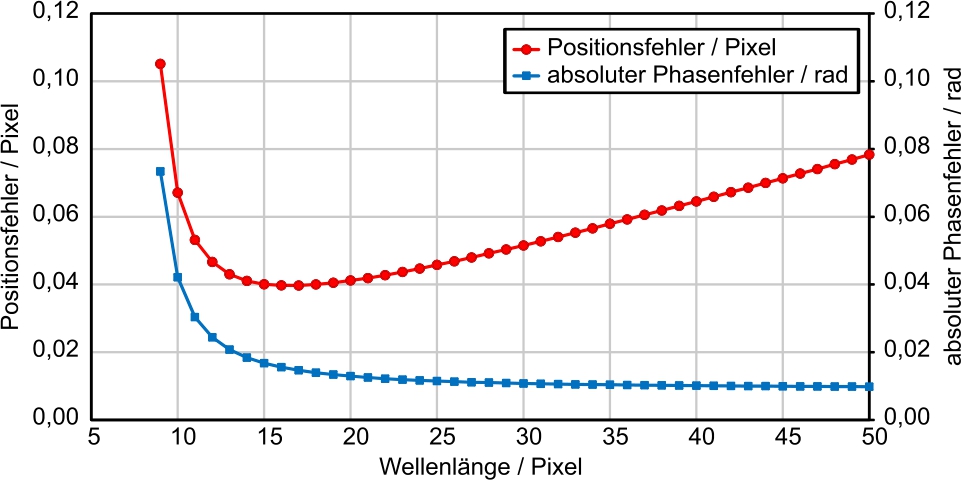
Experimentell ermittelte Minimierung der statistischen Positionsabweichung für eine gegebene Messsituation durch Bestimmung der optimalen Streifenbreite.

Aufschlussreich ist es, die von der Kamera bei den jeweiligen Wellenlängen registrierten Beleuchtungs- und Kontrastverhältnisse des Streifenmusters näher zu betrachten. In Abb. 9 sind hierzu in den oben erläuterten, von Belichtung β und Sichtbarkeit γ aufgespannten Parameterraum die zugehörigen Werte der Messreihe aus Abb. 8 eingetragen. Es ist zu erkennen, dass die Belichtung β wie zu erwarten keinerlei Abhängigkeit von der Wellenlänge zeigt, dass jedoch die Sichtbarkeit γ mit steigender Wellenlänge deutlich zunimmt. Das statistische Optimium bei einer Wellenlänge von 17 Pixel ist jedoch bemerkenswerter Weise von einer Sichtbarkeit von γopt≈0,6 gekennzeichnet, während die erzielten Maximalwerte für größere Wellenlängen bei γmax≈0,9 liegen. Dem menschlichen Betrachter stellt sich der Streifenkontrast bei der statistisch optimalen Streifenbreite daher als eher flau dar, weswegen bei rein intuitiver Einstellung der Streifenbreite eher zu große Werte gewählt werden und es somit zu einer vermeidbaren Zunahme der Unsicherheit der Ortskodierung kommt.

Abb. 9

Parameterraum von Belichtung und Sichtbarkeit, grüne Kreise: Verbesserung der Sichtbarkeit bei zunehmender Wellenlänge, rotes Quadrat: Sichtbarkeit mit minimaler statistischer Positionsabweichung bei Wellenlänge von 17 Pixel (vgl. Abb. 8).

7 Zusammenfassung

In dem vorliegenden Beitrag wird mit Blick auf geometrisch-optische Messverfahren mit strukturierter Beleuchtung, wie insbesondere der Streifenprojektion und der phasenmessenden Deflektometrie, eine vorteilhafte Ausführungsform des Heterodyn-Phasenschiebeverfahrens vorgestellt und hinsichtlich ihrer statistischen Eigenschaften analysiert. Im Mittelpunkt dieser Betrachtung stehen die Genese von Entfaltungsfehlern sowie deren mathematische Beschreibung. Im Ergebnis werden mathematisch fundierte Kriterien zur Bestimmung der beim Heterodynverfahren idealerweise zu verwendenden Wellenlängen formuliert und es wird aufgezeigt, dass bei Verwendung entsprechend optimierter Muster die Robustheit des Entfaltungsvorgangs gegenüber nicht optimierten Ansätzen um mehrere Größenordnungen gesteigert werden kann. Darüber hinaus wird eine auf dem linearen Kamerarauschmodell der EMVA 1288 basierende experimentelle Methodik vorgestellt, welche es ermöglicht, in einer konkreten Aufnahmesituation die im Hinblick auf die erzielbare statistische Unsicherheit der Ortskodierung optimale Basiswellenlänge zu ermitteln.