Crystal structure prediction using neural network potential and age-fitness Pareto genetic algorithm

Sadman Sadeed Omee; Lai Wei; Ming Hu; Jianjun Hu

doi:10.20517/jmi.2023.33

Download PDF

Research Article | Open Access | 1 Mar 2024

Crystal structure prediction using neural network potential and age-fitness Pareto genetic algorithm

Views: 861 | Downloads: 234 | Cited:

3

Sadman Sadeed Omee¹

,

Lai Wei¹

, ...

Jianjun Hu^*,1

J Mater Inf 2024;4:2.

10.20517/jmi.2023.33 | © The Author(s) 2024.

Author Information

Article Notes

Cite This Article

Abstract

While crystal structure prediction (CSP) remains a longstanding challenge, we introduce ParetoCSP, a novel algorithm for CSP, which combines a multi-objective genetic algorithm (GA) with a neural network inter-atomic potential model to find energetically optimal crystal structures given chemical compositions. We enhance the updated multi-objective GA (NSGA-III) by incorporating the genotypic age as an independent optimization criterion and employ the M3GNet universal inter-atomic potential to guide the GA search. Compared to GN-OA, a state-of-the-art neural potential-based CSP algorithm, ParetoCSP demonstrated significantly better predictive capabilities, outperforming by a factor of 2.562 across 55 diverse benchmark structures, as evaluated by seven performance metrics. Trajectory analysis of the traversed structures of all algorithms shows that ParetoCSP generated more valid structures than other algorithms, which helped guide the GA to search more effectively for the optimal structures. Our implementation code is available at https://github.com/sadmanomee/ParetoCSP.

Keywords

Neural network potential, genetic algorithm, age-fitness, Pareto optimization, crystal structure prediction

Download PDF 0 4

INTRODUCTION

Crystal structure prediction (CSP) is the problem of predicting the most energetically stable structure of a crystal given its chemical composition. Knowing the atomic structure is the most crucial aspect of comprehending crystalline materials. With the structural information of the material, advanced quantum-mechanical methods such as Density Functional Theory (DFT) can be utilized to calculate numerous physical characteristics of the crystal^[1]. As the physical and chemical characteristics of a crystal are dictated by the arrangement and composition of its atoms, CSP is critical to finding new materials that possess the needed properties such as high thermal conductivity, high compressing strength, high electrical conductivity, or low refractive index. CSP-based computational materials discovery is significant and has the potential to revolutionize a range of industries, such as those involving electric vehicles, Li batteries, building construction, energy storage, and quantum computing hardware ^[2–6]. For this reason, CSP, along with machine learning (ML)-based inverse design ^[5,7–10], has emerged as one of the most potential methods for finding novel materials.

Although there have been notable advancements in the field of CSP, the scientific community has yet to solve this fundamental challenge that has persisted for decades. CSP presents a significant challenge due to the requirement to search through an extensive range of potential configurations to identify the most stable arrangement of atoms of a crystal in a high-dimensional space. The complexity of CSP stems from the combinatorial nature of the optimization challenge, where the number of potential configurations grows exponentially with the number of atoms present in the crystal ^[1]. Additionally, the prediction of the most stable structure relies on several factors, including temperature, pressure, and chemical composition, further increasing the intricacy of the problem. Historically, the main method for determining crystal structures was through experimental X-ray diffraction (XRD) ^[11], which is time-consuming, expensive, and sometimes impossible, particularly for materials that are difficult to synthesize.

Computational approaches for CSP provide a faster and more affordable alternative than experimental methods. A typical strategy involves searching for the crystal's lowest energy atomic arrangement by optimizing its potential energy surface (PES) using different search algorithms. However, in some cases, simpler metrics such as the cohesive energy or the formation energy of the structures can be used instead ^[4]. The highly non-convex nature of the PES, which can contain a vast number of local minima, reduces the efficiency of the search algorithms. Moreover, finding the global minimum of a PES is categorized as an NP-hard problem ^[12]. Most research on the CSP problem concentrates on ab initio techniques, which involve exploring the atomic configuration space to locate the most stable structure based on the first-principles calculations of the free energy of possible structures ^[13–15]. Although these methods are highly accurate, the scalability and the applicability of these ab initio algorithms for predicting crystal structures remain a challenge. These methods are severely constrained because they rely on expensive first-principles DFT calculations ^[16,17] to determine the free energy of candidate structures. Furthermore, these methods are only applicable for predicting structures of comparatively small systems (< 10-20 atoms in the unit cell). Although there are inexpensive models available to estimate the free energy, they tend to have a poor correlation with reality, which can result in an inaccurate search ^[14]. For example, state-of-the-art (SOTA) graph neural networks (GNNs) have demonstrated the capability to accurately predict the formation energy of candidate structures ^[18–23], their performance on predicting non-stable or meta-stable structures is significantly lower as they are usually trained with stable crystals.

Several search algorithms have been applied to the CSP problem, including random sampling ^[12], simulated annealing ^[24–26], meta-dynamics ^[27,28], basin hopping ^[29,30], minima hopping ^[31], genetic algorithm (GA) ^[14,32–34], particle swarm optimization (PSO) ^[15], Bayesian optimization (BO) ^[35,36], and deep learning (DL) ^[37,38]. Among them, the USPEX (Universal Structure Predictor: Evolutionary Xtallography) algorithm, developed by Glass et al., is a prominent CSP algorithm based on evolutionary principles, using natural selection and reproduction to generate new crystal structures ^[14]. It incorporates a combination of three operators - heredity, mutation, and permutation to explore the configuration space. To evaluate candidate structures, they use ab initio free energy calculation using tools such as VASP ^[39] and SIESTA ^[40] which are highly accurate but extremely time-consuming. Another important CSP algorithm named CALYPSO (Crystal structure AnaLYsis by Particle Swarm Optimization) was devised by Wang et al., which employs a PSO algorithm to explore the energy landscape of crystal structures and identify the lowest energy structures ^[15]. To accomplish this, they developed a special strategy for removing comparable structures and applied symmetry-breaking restrictions to boost search effectiveness. Both USPEX and CALYPSO methods have been successfully applied to predict the crystal structures of diverse materials, including those under high-pressure conditions, complex oxides, alloys, etc. The random sampling-based CSP algorithms have also demonstrated their effectiveness. For example, AIRSS (Ab Initio Random Structure Searching) presented by Pickard et al. describes a scheme that generates diverse random crystal structures for various types of crystals and conducts DFT calculations on them to determine the most stable one^[12]. Another genre of CSP methods are template-based approaches ^[41–43], which involves finding an existing crystal structure as the template using some heuristic methods, or the ML method, etc., which has a similar chemical formula and then replacing some of its atoms with different elements. However, the accuracy of these models is constrained by the diversity and availability of the templates and the complexity of the target compound. Inspired by the recent success of DL-based methods in protein structure prediction ^[44–46], a DL-based algorithm, AlphaCrystal ^[38], has been designed to predict the contact map of a target crystal and then reconstruct its structure via a GA. However, the effectiveness of this model is constrained because its performance relies on the accuracy of the predicted space group, lattice parameters, and distance matrices. Moreover, it ultimately depends on the optimization algorithm for reconstructing the final structure from the contact map as it is unable to provide end-to-end prediction akin to DeepMind's AlphaFold$$ 2 $$^[45].

Compared to previous DFT-based CSP algorithms such as USPEX and CALYPSO, a major progress in CSP is to use ML potential models to replace the costly first-principle energy calculation. Cheng et al. developed a CSP framework named GN-OA, in which a GNN model was first trained to predict the formation energy and then an optimization algorithm was then used to search for the crystal structure with the minimum formation energy, guided by the GNN energy model ^[36]. They show that the BO search algorithm produces the best results among all optimization algorithms. However, predicting formation energy using GNNs has its drawbacks as its performance largely depends on the dataset it is trained on. A structure search trajectory analysis ^[47] also showed that current BO and PSO in GN-OA tend to generate too many invalid structures, which deteriorates its performance. While both USPEX and CALYPSO have been combined with ML potentials for CSP before GN-OA, they were only applicable to small crystal systems such as Carbon structures, Sodium under pressure, and Boron clusters ^[48,49] due to the limitation of their ML potential models. Recently, significant progress has been achieved in ML potentials for crystals ^[50–54] that can work with multi-element crystals and larger crystals systems. This will bring unprecedented opportunities and promise for modern CSP research and materials discovery. For example, recent advancement in deep neural network-based energy potential [M3GNet IAP (inter-atomic potential)]^[53] has shown its capability to cover $$ 89 $$ elements of the periodic table while the CHGNet ^[54] model was pre-trained on the energies, forces, stresses, and magnetic moments from the Materials Project Trajectory Dataset, consisting of ~1.5 million unstable and stable inorganic structures. It is intriguing to explore how well modern CSP algorithms based on these ML potentials can perform. Inspired by this progress, we propose the ParetoCSP algorithm for CSP, which combines the M3GNet potential with the age-fitness pareto GAs for efficient structure search. In this algorithm, candidate structures in the GA population are compared based on both the genotypic age and the formation energy, predicted by a neural network potential such as M3GNet or CHGNet. Compared to previous GN-OAs, we showed that the significant global search capability of our ParetoCSP allows it to achieve much better prediction performance.

Our contribution in this paper can be summarized as follows:

● We develop an efficient ParetoCSP for CSP, which combines an updated multi-objective GA (NSGA-III) by the inclusion of the age fitness Pareto optimization criterion and a neural network potential (M3GNet IAP), utilized to correlate crystal structures to their final energy.

● Our systematic evaluations on 55 benchmark crystals show that ParetoCSP outperforms GN-OA by a factor of 2.562 in terms of prediction accuracy.

● We reinforce GN-OA by replacing its formation energy predictor MEGNet (MatErials Graph Network) ^[19] with the M3GNet IAP final energy model and show that it improves the default GN-OA by a factor of 1.5 in terms of prediction accuracy. We further demonstrated the significant improvement in the search capability of ParetoCSP by showing that ParetoCSP outperforms the updated GN-OA by a factor of 1.71 in terms of prediction accuracy.

● We provide a quantitative analysis of the structures generated by ParetoCSP using seven performance metrics and empirically show that ParetoCSP found better quality structures for the test formulas than those by GN-OA.

● We perform a trajectory analysis of the generated structures by all evaluated CSP algorithms and show that ParetoCSP generates a significantly greater number of valid solutions than the GN-OA algorithm, which may have contributed to ParetoCSP's better performance in predicting the crystal structures.

METHOD

ParetoCSP: algorithm description

The input of our algorithm (ParetoCSP) is the elemental composition of a crystal $$ \{c_i\} $$, where $$ i $$ is the index of an atom and $$ c_i $$ is the element of the $$ i $$-th atom in the unit cell. A periodic crystal structure can be described by its lattice parameters ($$ L $$) $$ a, b, c $$ (representing the unit cell size), and $$ \alpha, \beta, \gamma $$ (representing angles in the unit cell), the space group, and the atomic coordinates at unique Wyckoff positions.

Our algorithm is based on the idea of the GN-OA algorithm ^[36] with two major upgrades, including the multi-objective GA search algorithm and the use of M3GNet potential for energy calculation. GN-OA has been proven from previous research that incorporating symmetry constraint expedites CSP ^[36,55]. Similar to the GN-OA approach, our method also considers CSP with symmetry constraints. We incorporate two additional structural features, namely crystal symmetry $$ S $$ and the occupancy of Wyckoff position $$ W_i $$ for each atom $$ i $$. These features are selected from a collection of $$ 229 $$ space groups and associated $$ 1506 $$ Wyckoff positions ^[56]. The method begins by selecting a symmetry $$ S $$ from the range of $$ P2 $$ to $$ P230 $$, followed by generating lattice parameters $$ L $$ within the chosen symmetry. Next, a combination of Wyckoff positions $$ \{W_i\} $$ is selected to fulfill the specified number of atoms in the cell. The atomic coordinates $$ \{R_i\} $$ are then determined based on the chosen Wyckoff positions $$ \{W_i\} $$ and lattice parameters $$ L $$. To generate crystal structures, we need to tune the $$ S $$, $$ \{W_i\} $$, $$ L $$, and $$ \{R_i\} $$ variables.

By selecting different combinations of $$ S $$, $$ {W_i} $$, $$ L $$, and $$ {R_i} $$, we can generate a comprehensive array of possible crystal structures for the given $$ {c_i} $$. In theory, determining the energy of these various structures and selecting the one with the least energy should be the optimal crystal arrangement. However, exhaustively enumerating all these structures becomes practically infeasible due to the staggering number of potential combinations. To address this complexity, a more practical approach involves iteratively sampling candidate structures from the design space, under the assumption that one of the sampled structures will emerge as the most stable and optimal solution. Consequently, we adopt an optimization strategy to guide this search process towards identifying the structure with the lowest energy. In particular, we utilize a GA, NSGA-III ^[57,58], improved by incorporating age-fitness Pareto optimization (AFPO) ^[59] to enhance its performance and robustness.

First, we generate $$ n $$ initial random structures. We then assign them an age of 1 and convert them into crystal graphs. There are multiple approaches to encode crystals as graphs ^{[18,19,60–62]}. In short, we can consider each atom of the crystal as nodes of the graph, and interactions between them (e.g., bonds) can be encoded as edges. Interactions can be limited to a certain cutoff range to define more realistic graphs. Each node and edge need to be assigned feature vectors for the DNN to learn the specific property. After generating the initial structures, we predict their final energy/atom using the M3GNet universal IAP ^[53]. Next, we calculate fitness considering both energy and age of the generated crystals (two independent dimensions in the Pareto front). After that, we check whether the total number of generations is less than a certain threshold $$ \mathcal{G} $$. If yes, we increase the age of all individuals by 1. This follows the Pareto tournament selection, which selects the parents among the individual structures for the next generation. We usually set the tournament size to 2 which selects half of the population as parents.

Next, we perform the genetic operations - crossover and mutation. After crossover, we update the age of each individual by inheriting the maximum age of corresponding parents. Similarly, after mutation, individual ages are updated by inheriting the age of their respective parents. These operations result in a new population of $$ n $$ individuals for the next generation. The concept of age ensures a diverse population by containing both old and young individuals and effectively prevents from converging into local optima ^[59]. We then increase the generation number and repeat the whole process by calculating the final energy/atom of each structure until the generation number $$ \leq $$ the threshold $$ \mathcal{G} $$. After finishing $$ \mathcal{G} $$. generations, we obtain a set of $$ \mathcal{F} $$ non-dominated solutions on the Pareto front. We select the solution with the lowest final energy per atom as the optimal solution. We further relax the structure using the structure relaxation method of M3GNet IAP, which produces a more refined structure with lower final energy per atom. Finally, we perform a symmetrization operation to symmetrize the structure to output the final structure. Figure 1 shows the flowchart of our ParetoCSP algorithm.

Crystal structure prediction using neural network potential and age-fitness Pareto genetic algorithm

Figure 1. The flowchart of ParetoCSP algorithm. It starts by generating $$ n $$ random crystals and assigning them an age of $$ 1 $$, where $$ n $$ denotes the population size. One complete generation then goes through the following steps: calculating energy of the structures and fitness, selecting parents, performing genetic operations, and updating the age. After a certain threshold of $$ \mathcal{G} $$ generations, the lowest energy structure from the multi-dimensional Pareto front is chosen and further relaxed and symmetrized to obtain the final optimal structure. The genetic encoding is shown in the lower right corner of the flowchart. It contains lattice parameters $$ a $$, $$ b $$, $$ c $$, $$ \alpha $$, $$ \beta $$, and $$ \gamma $$, the space group $$ S $$, the wyckoff position combination $$ W_i $$, and the atomic coordinates $$ R_i $$ of atom indexed by $$ i $$.

AFPO

One of the key requirements for a GA to achieve a robust global search is to maintain the diversity of the population. Here, we employed the multi-objective GA, AFPO by Schmidt and Lipson ^[59], to achieve this goal. The AFPO algorithm is inspired by the idea of age-layered population structure (ALPS) ^[63,64], which divides the evolving population into layers based on how long the genetic material has been present in the population so that competitions happen at different fitness levels, avoiding the occurrence of premature convergence. The age of an individual is defined as how long the oldest part of its genotype has been present in the population ^[65]. Instead of partitioning the population into layers as done in the Hierarchical Fair Competition (HFC) algorithm ^[63], AFPO uses age as an explicit optimization criterion (an independent dimension in a multi-objective Pareto front). A solution is considered optimal if it has both higher fitness and lower age compared to others. This enables the algorithm to maintain diversity in the population, avoid premature convergence to local optima, and find better solutions at faster convergence speed ^[59]. The AFPO algorithm starts by initializing a population of $$ N $$ individuals randomly and assigns an age of one to all of them. The fitness of an individual is evaluated by calculating its performance for all objectives. The fitness values are then used to rank the individuals based on their Pareto dominance. The algorithm then updates and assigns the age for each individual. The age of an individual is increased by one with each generation. When crossover or mutation occurs, the individual's age is set to the maximum age of its parents. The algorithm uses a parameter called the tournament size $$ K $$ which determines the number of individuals that compete for selection. Specifically, $$ K $$ individuals are selected at random. It then forms the Pareto front among them, eliminating any dominated individuals. After that, crossovers and mutations are applied to the parents to generate offspring. The objective function values for each offspring are evaluated and the updated ages are assigned to each offspring. The newly generated offspring replace some of the older individuals in the population based on their age and fitness values. To avoid premature convergence towards sub-optimal solutions, a few new random individuals are added to the population in each generation to maintain diversity. The algorithm continues to iterate through the above steps until a stopping criterion is met, such as a maximum number of generations or a desired level of convergence. For more details, the readers are referred to the ref ^[65].

NSGA-III: multi-objective GA

We use the NSGA-III ^[57] algorithm to implement the age-fitness-based GA AFPO. NSGA-III is an improved version of the popular multi-objective evolutionary algorithm NSGA-II ^[66]. Here, we describe the NSGA-III framework as defined in reference ^[57,58]. The NSGA-III algorithm begins with defining a group of reference points. To create an offspring population $$ Q_i $$ at generation $$ i $$, the current parent population $$ P_i $$ undergoes genetic operations. The resulting population, $$ P_i \cup Q_i $$, is then sorted based on their nondomination levels ($$ F_1, F_2, $$, and so on). The algorithm saves all members up to the last fully accommodated level, $$ F_k $$ (considering all solutions from level ($$ k + 1 $$) onward are rejected) in a set called $$ \delta_i $$. The individuals from $$ \delta_i\setminus F_k $$ have already been chosen for the next set of candidates, while the remaining spots are filled by individuals from $$ F_k $$.

The selection process of NSGA-III is substantially altered from the approach used in NSGA-II. First, the objective values and reference points are normalized. Second, each member in $$ \delta_i $$ is assigned a reference point based on its distance to the individual with a reference line formed by connecting the ideal point to the reference point. This method enables the determination of the number and positions of population members linked to each supplied reference point in $$ \delta\setminus F_k $$. Next, a niching technique is applied to pick individuals from $$ F_k $$ who are underrepresented in $$ \delta_i\setminus F_k $$ based on the results of the association process explained earlier. Reference points with the fewest number of associations in the $$ \delta\setminus F_k $$ population are identified and corresponding points in the $$ F_k $$ set are searched. These selected members from $$ F_k $$ are then added to the population, one by one, until the required population size is achieved. Thus, NSGA-III utilizes a different approach in contrast to NSGA-II to sustain diversity among population members by incorporating a set of well-distributed reference points that are provided initially and updated adaptively during the algorithm's execution ^[58]. More implementation details can be found in ref ^[67].

M3GNet inter-atomic potential

Energy potential is one of the key components of modern CSP algorithms. Here, we use M3GNet ^[53], which is a GNN-based ML potential model that explicitly incorporates $$ 3 $$-body interactions. This model combines the graph-based DL inter-atomic potential (IAP) and the many-body features found in traditional IAPs with the flexible graph material representations. One notable distinction of M3GNet from previous material graph implementations is the inclusion of atom coordinates and the 3 × 3 lattice matrix in crystals. These additions are essential for obtaining tensorial quantities such as forces and stresses through the use of auto-differentiation.

In the M3GNet model, position-included graphs serve as inputs. Graph features include embedded atomic numbers of elements and pair bond distances. Similar to traditional GNNs, the node and the edge features are updated via the graph convolution operations. Architecturally, there are several differences between M3GNet and MEGNet. For example, M3GNet utilizes angle information between bonds, but MEGNet does not. Unlike MEGNet, M3GNet has the many-body computation module that was proven essential for its excellent performance. Additionally, M3GNet uses gated multi-layer perceptron (MLP) for obtaining atomic energy in contrast to MEGNet. Our M3GNet potential was trained using both stable and unstable structures so that it can well capture the difference between these two. For details about the training, we refer the readers to the M3GNet paper ^[53]. The dataset used for training the M3GNet model is much larger than that for the MEGNet model, and it contains both stable and unstable structures which makes M3GNet more specialized in predicting energies of the intermediate unstable structures of crystals. The precise and efficient relaxation of diverse crystal structures and the accurate energy prediction achieved by the M3GNet-based relaxation algorithm make it well-suited for large-scale and fast CSP.

Evaluation criteria

Many earlier studies ^[12,14,15] have depended on manual structural examination and ab initio formation energy comparison to assess the performance of a CSP algorithm. However, these metrics do not address the situation that an algorithm may not find the exact solution for a crystal, and it is not clear how much the generated structure deviates from the ground truth structure. Usually, previous works did not quantitatively report how good or bad a solution is. Also, if two algorithms fail to generate the exact crystal structure, these metrics do not describe which one is closer to finding the optimal solution. Recently, Wei et al. proposed a set of performance metrics to measure CSP performance which alleviated this issue greatly ^[47]. We used seven performance metrics from that work to measure the performance of our CSP algorithm and the baselines. The required data are the crystallographic information file (CIF) of both the optimized and relaxed final structure generated by the CSP algorithm and its corresponding ground truth stable structure. Details about these performance metrics can be found in ref^[47]. They are shortly listed below:

1. Energy distance (ED)

2. Wyckoff position fraction coordinate root mean squared error distance (W$$ _{rmse} $$)

3. Wyckoff position fraction coordinate root mean absolute error (W$$ _{mae} $$)

4. Sinkhorn distance (SD)

5. Chamfer distance (CD)

6. Hausdorff distance (HD)

7. Crystal fingerprint distance (FP)

RESULTS

Our objective is to demonstrate the effectiveness of ParetoCSP for CSP by showing that the multi-objective AFPO GA enables a much more effective structure search method than the BO and PSO and that M3GNet IAP is a more powerful crystal energy predictor than the previous MEGNet model.

Benchmark set description

We selected a diverse set of $$ 55 $$ stable structures available in the Materials Project database ^[68] with no more than $$ 20 $$ atoms. Among them, $$ 20 $$ are binary crystals, $$ 20 $$ are ternary crystals, and $$ 15 $$ are quarternary crystals. We chose the benchmark set based on multiple factors such as diversity of elements, diversity of space groups, special types of materials (e.g., perovskites), usage in previous CSP literature, etc. Supplementary Figure 1A shows the diversity of the elements used in the benchmark set. Table 1 shows the detailed information about the $$ 55 $$ chosen test crystals used in this work.

Table 1

Details of the $$ 55 $$ benchmark crystals used in this work

Composition	No. ofatoms	Space group	Formation energy(eV/atom)	Final energy(eV/atom)	M3GNet final energy(eV/atom)
The first $$20$$ crystals are binary, the second $$20$$ crystals are ternary, and the last $$15$$ crystals are quarternary, and each of these types of crystals is separated by single horizontal lines. We can see that the ground truth final energies and the predicted final energies by M3GNet IAP are very close, demonstrating the effectiveness of M3GNet as an energy predictor.
TiCo	$$ 2 $$	$$ Pm-3m $$	$$ -0.401 $$	$$ -7.9003 $$	$$ -7.8986 $$
CrPd$$ _3 $$	$$ 4 $$	$$ Pm-3m $$	$$ -0.074 $$	$$ -6.3722 $$	$$ -6.4341 $$
GaNi$$ _3 $$	$$ 4 $$	$$ Pm-3m $$	$$ -0.291 $$	$$ -5.3813 $$	$$ -5.3806 $$
ZrSe$$ _2 $$	$$ 3 $$	$$ P-3m1 $$	$$ -1.581 $$	$$ -6.5087 $$	$$ -6.5077 $$
MnAl	$$ 2 $$	$$ Pm-3m $$	$$ -0.225 $$	$$ -6.6784 $$	$$ -6.7503 $$
NiS$$ _2 $$	$$ 6 $$	$$ P6_3/mmc $$	$$ -0.4 $$	$$ -4.7493 $$	$$ -4.9189 $$
TiO$$ _2 $$	$$ 6 $$	$$ P4_2/mnm $$	$$ -3.312 $$	$$ -8.9369 $$	$$ -8.9290 $$
NiCl	$$ 4 $$	$$ P6_3mc $$	$$ -0.362 $$	$$ -3.8391 $$	$$ -3.8899 $$
AlNi$$ _3 $$	$$ 4 $$	$$ Pm-3m $$	$$ -0.426 $$	$$ -5.7047 $$	$$ -5.6909 $$
CuBr	$$ 4 $$	$$ P6_3/mmc $$	$$ -0.519 $$	$$ -3.0777 $$	$$ -3.0908 $$
VPt$$ _3 $$	$$ 8 $$	$$ I4/mmm $$	$$ -0.443 $$	$$ -7.2678 $$	$$ -7.2638 $$
MnCo	$$ 2 $$	$$ Pm-3m $$	$$ -0.0259 $$	$$ -7.6954 $$	$$ -7.6963 $$
BN	$$ 4 $$	$$ P6_3/mmc $$	$$ -1.411 $$	$$ -8.7853 $$	$$ -8.7551 $$
GeMo$$ _3 $$	$$ 8 $$	$$ Pm-3n $$	$$ -0.15 $$	$$ -9.4398 $$	$$ -9.3588 $$
Ca$$ _3 $$V	$$ 8 $$	$$ I4/mmm $$	$$ 0.481 $$	$$ -3.2942 $$	$$ -3.1638 $$
Ga$$ _2 $$Te$$ _3 $$	$$ 20 $$	$$ Cc $$	$$ -0.575 $$	$$ -3.4181 $$	$$ -3.4160 $$
CoAs$$ _2 $$	$$ 12 $$	$$ P2_1/c $$	$$ -0.29 $$	$$ -5.8013 $$	$$ -5.7964 $$
Li$$ _2 $$Al	$$ 12 $$	$$ Cmcm $$	$$ -0.163 $$	$$ -2.6841 $$	$$ -2.6623 $$
VS	$$ 4 $$	$$ P6_3/mmc $$	$$ -0.797 $$	$$ -7.1557 $$	$$ -7.3701 $$
Ba$$ _2 $$Hg	$$ 6 $$	$$ I4/mmm $$	$$ -0.384 $$	$$ -1.7645 $$	$$ -1.7582 $$
SrTiO$$ _3 $$	$$ 5 $$	$$ Pm-3m $$	$$ -3.552 $$	$$ -8.0249 $$	$$ -8.0168 $$
Al$$ _2 $$FeCo	$$ 4 $$	$$ P4/mmm $$	$$ -0.472 $$	$$ -6.2398 $$	$$ -6.2462 $$
GaBN$$ _2 $$	$$ 4 $$	$$ P-4m2 $$	$$ -0.675 $$	$$ -7.0893 $$	$$ -7.0918 $$
AcMnO$$ _3 $$	$$ 5 $$	$$ Pm-3m $$	$$ -2.971 $$	$$ -7.1651 $$	$$ -7.8733 $$
PaTlO$$ _3 $$	$$ 5 $$	$$ Pm-3m $$	$$ -2.995 $$	$$ -8.1070 $$	$$ -8.1012 $$
CdCuN	$$ 3 $$	$$ P-6m2 $$	$$ 0.249 $$	$$ -4.0807 $$	$$ -4.0228 $$
HoHSe	$$ 3 $$	$$ P-6m2 $$	$$ -1.65 $$	$$ -5.2538 $$	$$ -5.2245 $$
Li$$ _2 $$ZnSi	$$ 8 $$	$$ P6_3/mmc $$	$$ 0.0512 $$	$$ -2.5923 $$	$$ -2.6308 $$
Cd$$ _2 $$AgPt	$$ 16 $$	$$ Fm-3m $$	$$ -0.195 $$	$$ -2.8829 $$	$$ -2.8415 $$
AlCrFe$$ _2 $$	$$ 4 $$	$$ P4/mmm $$	$$ -0.157 $$	$$ -7.7417 $$	$$ -7.6908 $$
ZnCdPt$$ _2 $$	$$ 4 $$	$$ P4/mmm $$	$$ -0.444 $$	$$ -4.0253 $$	$$ -4.0164 $$
EuAlSi	$$ 3 $$	$$ P-6m2 $$	$$ -0.475 $$	$$ -6.9741 $$	$$ -6.9345 $$
Sc$$ _3 $$TlC	$$ 5 $$	$$ Pm-3m $$	$$ -0.622 $$	$$ -6.7381 $$	$$ -6.7419 $$
GaSeCl	$$ 12 $$	$$ Pnnm $$	$$ -1.216 $$	$$ -3.6174 $$	$$ -3.6262 $$
CaAgN	$$ 3 $$	$$ P-6m2 $$	$$ -0.278 $$	$$ -4.5501 $$	$$ -4.7050 $$
BaAlGe	$$ 3 $$	$$ P-6m2 $$	$$ -0.476 $$	$$ -3.9051 $$	$$ -3.9051 $$
K$$ _2 $$PdS$$ _2 $$	$$ 10 $$	$$ Immm $$	$$ -1.103 $$	$$ -4.0349 $$	$$ -4.0066 $$
KCrO$$ _2 $$	$$ 8 $$	$$ P6_3/mmc $$	$$ -2.117 $$	$$ -6.4452 $$	$$ -6.4248 $$
TiZnCu$$ _2 $$	$$ 4 $$	$$ P4/mmm $$	$$ -0.0774 $$	$$ -4.4119 $$	$$ -4.4876 $$
Ta$$ _2 $$N$$ _3 $$O	$$ 6 $$	$$ P6/mmm $$	$$ -0.723 $$	$$ -9.3783 $$	$$ -9.3848 $$
AgBiSeS	$$ 4 $$	$$ P4/mmm $$	$$ -0.404 $$	$$ -3.7363 $$	$$ -3.8289 $$
ZrTaNO	$$ 4 $$	$$ P-6m2 $$	$$ -1.381 $$	$$ -9.5450 $$	$$ -9.5429 $$
MnAlCuPd	$$ 4 $$	$$ P4mm $$	$$ -0.3 $$	$$ -5.8467 $$	$$ -5.8774 $$
CsNaICl	$$ 4 $$	$$ P4/mmm $$	$$ -1.79 $$	$$ -2.9280 $$	$$ -2.9448 $$
DyThCN	$$ 4 $$	$$ P4/mmm $$	$$ -1.03 $$	$$ -8.3316 $$	$$ -8.3510 $$
Li$$ _2 $$MgCdP$$ _2 $$	$$ 6 $$	$$ P-4m2 $$	$$ -0.61 $$	$$ -3.4699 $$	$$ -3.4514 $$
SrWNO$$ _2 $$	$$ 5 $$	$$ P4/mmm $$	$$ -1.88 $$	$$ -7.2188 $$	$$ -7.0886 $$
Sr$$ _2 $$BBrN$$ _2 $$	$$ 18 $$	$$ R-3m $$	$$ -1.639 $$	$$ -6.1437 $$	$$ -6.1501 $$
ZrCuSiAs	$$ 8 $$	$$ P4/nmm $$	$$ -0.592 $$	$$ -6.2924 $$	$$ -6.2853 $$
NdNiSnH$$ _2 $$	$$ 10 $$	$$ P6_3/mmc $$	$$ -0.599 $$	$$ -4.7970 $$	$$ -4.8101 $$
MnCoSnRh	$$ 12 $$	$$ F-43m $$	$$ -0.25 $$	$$ -7.1676 $$	$$ -7.1093 $$
Mg$$ _2 $$ZnB$$ _2 $$Ir$$ _5 $$	$$ 20 $$	$$ P4/mbm $$	$$ -0.454 $$	$$ -6.6614 $$	$$ -6.6577 $$
AlCr$$ _4 $$GaC$$ _2 $$	$$ 8 $$	$$ P-6m2 $$	$$ -0.151 $$	$$ -8.1314 $$	$$ -8.1246 $$
Y$$ _3 $$Al$$ _3 $$NiGe$$ _2 $$	$$ 9 $$	$$ P-62m $$	$$ -0.735 $$	$$ -5.8214 $$	$$ -5.8305 $$
Ba$$ _2 $$CeTaO$$ _6 $$	$$ 20 $$	$$ C2/m $$	$$ -3.49 $$	$$ -8.2048 $$	$$ -8.2384 $$

Performance analysis of ParetoCSP

The default version of ParetoCSP uses M3GNet universal IAP as the final energy evaluator for the candidate structures to guide the AFPO-based GA in identifying the most stable structure with the minimum energy. Our algorithm ParetoCSP predicted the exact structures for $$ 17 $$ out $$ 20 $$ binary crystals ($$ 85\% $$), $$ 16 $$ out of $$ 20 $$ ternary crystals ($$ 80\% $$), and $$ 8 $$ out of $$ 15 $$ quarternary crystals ($$ 53.333\% $$) [Table 2]. Overall, ParetoCSP achieved an accuracy of $$ 74.55\% $$ among all $$ 55 $$ test crystals for this research, which is the highest among all evaluated algorithms ($$ \approx 1.71\times $$ the next best algorithm). Details on comparison with other algorithms and energy methods are discussed in Subsections 3.3 and 3.4. The exact accuracy results for all algorithms are presented in Table 2. All the structures were assigned ✔ (exact) or ✘ (non-exact) based on manual inspection which was predominantly done in the majority of the past literature ^[15,36].

Table 2

Performance comparison of ParetoCSP with baseline algorithms

Composition	ParetoCSPwith M3GNet (Default)	ParetoCSPwith MEGNet	GN-OAwith M3GNet	GN-OAwith MEGNet (Default)
Successful and failed predictions via manual inspection are denoted by a ✔ and ✘, respectively. ParetoCSP with M3GNet achieved the highest success rate in finding the exact structures of these crystals; GN-OA with M3GNet achieved the second best success rate. ParetoCSP with MEGNet performed as the third-best, while GN-OA with MEGNet performed the poorest. These results highlight the significant impact of using M3GNet IAP as a crystal final energy predictor and structure relaxer and the effectiveness of the AFPO-based GA as a structure search function.AFPO: age-fitness Pareto optimization.
TiCo	✔	✔	✔	✘
CrPd$$_3$$	✔	✔	✘	✘
GaNi$$_3$$	✔	✔	✔	✔
ZrSe$$_2$$	✔	✔	✔	✔
MnAl	✔	✔	✔	✔
NiS$$_2$$	✔	✘	✔	✔
TiO$$_2$$	✔	✔	✔	✔
NiCl	✔	✘	✘	✘
AlNi$$_3$$	✔	✔	✔	✔
CuBr	✔	✘	✘	✘
VPt$$_3$$	✔	✔	✔	✔
MnCo	✔	✔	✔	✔
BN	✔	✔	✔	✔
GeMo$$_3$$	✔	✔	✔	✔
Ca$$_3$$V	✔	✔	✘	✘
Ga$$_2$$Te$$_3$$	✘	✘	✘	✘
CoAs$$_2$$	✔	✘	✘	✘
Li$$_2$$Al	✘	✘	✘	✘
VS	✔	✘	✔	✘
Ba$$_2$$Hg	✘	✘	✘	✘
SrTiO$$_3$$	✔	✔	✔	✔
Al$$_2$$FeCo	✔	✔	✘	✘
GaBN$$_2$$	✔	✔	✘	✘
AcMnO$$_3$$	✔	✔	✔	✔
PaTlO$$_3$$	✔	✔	✔	✔
CdCuN	✔	✘	✘	✘
HoHSe	✔	✘	✔	✘
Li$$_2$$ZnSi	✘	✘	✘	✘
Cd$$_2$$AgPt	✘	✘	✘	✘
AlCrFe$$_2$$	✔	✘	✘	✘
ZnCdPt$$_2$$	✔	✘	✘	✘
EuAlSi	✔	✘	✔	✔
Sc$$_3$$TlC	✔	✔	✔	✔
GaSeCl	✘	✘	✘	✘
CaAgN	✔	✘	✔	✘
BaAlGe	✔	✔	✔	✘
K$$_2$$PdS$$_2$$	✘	✘	✘	✘
KCrO$$_2$$	✔	✘	✘	✘
TiZnCu$$_2$$	✔	✔	✔	✔
Ta$$_2$$N$$_3$$O	✔	✘	✘	✘
AgBiSeS	✔	✔	✘	✘
ZrTaNO	✔	✘	✔	✘
MnAlCuPd	✔	✘	✘	✘
CsNaICl	✔	✘	✔	✘
DyThCN	✔	✘	✔	✘
Li$$_2$$MgCdP$$_2$$	✘	✘	✘	✘
SrWNO$$_2$$	✔	✘	✘	✘
Sr$$_2$$BBrN$$_2$$	✘	✘	✘	✘
ZrCuSiAs	✘	✘	✘	✘
NdNiSnH$$_2$$	✘	✘	✘	✘
MnCoSnRh	✘	✘	✘	✘
Mg$$_2$$ZnB$$_2$$Ir$$_5$$	✘	✘	✘	✘
AlCr$$_4$$GaC$$_2$$	✔	✔	✘	✘
Y$$_3$$Al$$_3$$NiGe$$_2$$	✔	✘	✘	✘
Ba$$_2$$CeTaO$$_6$$	✘	✘	✘	✘
Accuracy	Overall: $$74.55\%$$	Overall: $$40\%$$	Overall: $$43.636\%$$	Overall: $$29.091\%$$
	Binary: $$85\%$$	Binary: $$60\%$$	Binary: $$60\%$$	Binary: $$50\%$$
	Ternary: $$80\%$$	Ternary: $$40\%$$	Ternary: $$45\%$$	Ternary: $$30\%$$
	Quarternary: $$53.333\%$$	Quarternary: $$13.333\%$$	Quarternary: $$20\%$$	Quarternary: $$0\%$$

We observed that ParetoCSP successfully found the most stable structures of all cubic and hexagonal binary crystals and most tetragonal binary crystals in the benchmark dataset. The three unsuccessful binary crystals that ParetoCSP failed to identify their exact structures are Ga$$ _2 $$Te$$ _3 $$ (monoclinic), Li$$ _2 $$Al (orthorhombic), and Ba$$ _2 $$Hg (tetragonal). For ternary crystals, ParetoCSP successfully determined the exact stable structures for all tetragonal crystals and most cubic and hexagonal crystals. However, there were four instances where the prediction failed, namely for Li$$ _2 $$ZnSi (hexagonal), Cd$$ _2 $$AgPt (cubic), GaSeCl (orthorhombic), and K$$ _2 $$PdS$$ _2 $$ (orthorhombic). In the case of quarternary crystals, ParetoCSP achieved dominance over most hexagonal and tetragonal structures. Li$$ _2 $$MgCdP$$ _2 $$ (tetragonal), Sr$$ _2 $$BBrN$$ _2 $$ (trigonal), ZrCuSiAs (tetragonal), NdNiSnH$$ _2 $$ (hexagonal), MnCoSnRh (cubic), Mg$$ _2 $$ZnB$$ _2 $$Ir$$ _5 $$ (tetragonal), Ba$$ _2 $$CeTaO$$ _6 $$ (monoclinic) are the seven quarternary failure cases for ParetoCSP in terms of finding exact structures. Based on these observations, we can claim that ParetoCSP combined with M3GNet IAP demonstrated notable efficacy in predicting cubic, hexagonal, and tetragonal crystalline materials. However, its performance in predicting monoclinic and orthorhombic crystals is comparatively less successful. This can be accounted for due to the higher number of degrees of freedom of monoclinic and orthorhombic crystal systems compared to simpler crystal systems such as cubic or hexagonal. Also, monoclinic and orthorhombic crystals have a varied range of complex structural motifs, which makes it difficult for CSP algorithms to predict their exact structures. However, this does not diminish the claim that our algorithm is the best among the four ML potential-based CSP algorithms evaluated here. Later, we demonstrated that the other CSP algorithms also faced similar challenges. Ground truth and predicted structures of sample crystals are shown in Figure 2 using the VESTA tool, which contains examples of both successful and unsuccessful predictions.

Figure 2. Sample structure prediction by ParetoCSP. Every ground truth structure is followed by the predicted structure. (A- P) show that the structures of MnAl, ZrSe$$ _2 $$, GeMo$$ _3 $$, SrTiO$$ _3 $$, Ta$$ _2 $$N$$ _3 $$O, and GaBN$$ _2 $$ were successfully predicted, while (Q - T) show that ParetoCSP was unable to predict the structures of GaSeCl, and NdNiSnH$$ _2 $$. All the structures were visualized using VESTA. For better visualization, we set the fractional coordinate ranges of all axes to a maximum of $$ 3 $$ for Ta$$ _2 $$N$$ _3 $$O, GaBN$$ _2 $$, and GaSeCl, and we used the space-filling style for Ta$$ _2 $$N$$ _3 $$O, and GaSeCl. Besides these, we set the fractional coordinate ranges of all axes to a maximum of $$ 1 $$ for all structures and used the ball-and-stick style.

Now, we analyze the performance of ParetoCSP in terms of the quantitative performance metrics. As mentioned before, we used a set of seven performance metrics to evaluate the prediction performance of different CSP algorithms. The values of each performance metric for all $$ 55 $$ chosen crystals are shown in Table 3. Ideally, all the performance metric values should be zero if the predicted structure and the ground truth structure are exactly the same. We identified the values of the failure cases which indicate the poor quality of the predictions. The process for determining them involved identifying the highest value for each performance metric among all successful predictions (we name them satisfactory values) and then selecting the values that exceeded those for the failed predictions. We have highlighted these values in bold letters in Table 3. We noticed that with the exception of K$$ _2 $$PdS$$ _2 $$ and ZrCuSiAs, all but $$ 12 $$ of the failed cases demonstrated higher energy distance values compared to the satisfactory energy distance value ($$ 0.7301 $$ eV/atom), indicating non-optimal predicted structures. Similarly, for Sinkhorn distance (SD), apart from ZrCuSiAs, the remaining $$ 13 $$ unsuccessful predictions exhibited significantly higher values than the satisfactory SD value ($$ 5.6727 $$ Å), suggesting poor prediction quality. For W$$ _{rmse} $$ and W$$ _{mae} $$, we assigned a cross ($$ \times $$) to indicate if the predicted structure and the target structure do not have similar wyckoff position configurations in the symmetrized structures, and thus, they cannot be calculated. We observed that $$ 11 $$ out of $$ 14 $$ failed predictions (symmetrized) do not have a similar wyckoff position compared to the ground truth symmetrized structure, indicating unsuccessful predictions. However, for the Chamfer distance (CD) metric, only $$ 6 $$ out of $$ 14 $$ failed predictions displayed higher quantities than the satisfactory CD value ($$ 3.8432 $$ Å), indicating that CD was not the most suitable metric for measuring prediction quality in crystal structures for our algorithm. In contrast, Hausdorff distance (HD) showed that $$ 10 $$ out of $$ 14 $$ failed predictions had higher values than the satisfactory HD value ($$ 3.7665 $$ Å). Notably, the only performance metric that consistently distinguished between optimal and non-optimal structures across all failed predictions is the crystal fingerprint (FP) metric (satisfactory value: $$ 0.9943 $$), demonstrating its effectiveness in capturing the differences between these structures. In conclusion, all the metrics provided strong evidence of the non-optimal nature of the $$ 14 $$ failed structures.

Table 3

Quantitative performance metrics of ParetoCSP with M3GNet for the $$ 55 $$ benchmark crystals evaluated in this work

Crystal	ED	$$ W_{rmse} $$	$$ W_{mae} $$	SD	CD	HD	FP
For each metric and each failure case, the values, which are greater than the range of exact predictions, are denoted by bold letters to mark as high values that quantitatively shows their non-optimality. Binary, ternary, and quarternary crystals are separated by single horizontal lines.
TiCo	$$ 0.0009 $$	$$ 0.0 $$	$$ 0.0 $$	$$ 0.007 $$	$$ 0.007 $$	$$ 0.007 $$	$$ 0.0 $$
CrPd$$ _3 $$	$$ 0.0071 $$	$$ 0.0 $$	$$ 0.0 $$	$$ 0.0408 $$	$$ 0.0204 $$	$$ 0.0136 $$	$$ 0.0 $$
GaNi$$ _3 $$	$$ 0.0355 $$	$$ 0.0 $$	$$ 0.0 $$	$$ 0.0839 $$	$$ 0.042 $$	$$ 0.028 $$	$$ 0.0 $$
ZrSe$$ _2 $$	$$ 0.0206 $$	$$ 0.0062 $$	$$ 0.0025 $$	$$ 0.6353 $$	$$ 0.4235 $$	$$ 0.5848 $$	$$ 0.3243 $$
MnAl	$$ 0.0 $$	$$ 0.0 $$	$$ 0.0 $$	$$ 0.0002 $$	$$ 0.0002 $$	$$ 0.0002 $$	$$ 0.0 $$
NiS$$ _2 $$	$$ 0.2016 $$	$$ 0.2889 $$	$$ 0.2303 $$	$$ 5.6727 $$	$$ 3.8432 $$	$$ 3.7665 $$	$$ 0.269 $$
TiO$$ _2 $$	$$ 0.6931 $$	$$ 0.2304 $$	$$ 0.1431 $$	$$ 4.209 $$	$$ 2.8535 $$	$$ 1.8551 $$	$$ 0.9793 $$
NiCl	$$ 0.3284 $$	$$ 0.2562 $$	$$ 0.1723 $$	$$ 1.3811 $$	$$ 2.3407 $$	$$ 1.1495 $$	$$ 0.6431 $$
AlNi$$ _3 $$	$$ 0.0234 $$	$$ 0.0 $$	$$ 0.0 $$	$$ 0.0727 $$	$$ 0.0363 $$	$$ 0.0242 $$	$$ 0.0 $$
CuBr	$$ 0.3225 $$	$$ 0.2521 $$	$$ 0.1784 $$	$$ 1.8724 $$	$$ 2.5043 $$	$$ 1.0065 $$	$$ 0.3054 $$
VPt$$ _3 $$	$$ 0.2415 $$	$$ 0.3235 $$	$$ 0.2411 $$	$$ 1.3424 $$	$$ 0.2395 $$	$$ 0.2805 $$	$$ 0.1772 $$
MnCo	$$ 0.0 $$	$$ 0.0 $$	$$ 0.0 $$	$$ 0.0001 $$	$$ 0.0001 $$	$$ 0.0001 $$	$$ 0.0 $$
BN	$$ 0.3643 $$	$$ 0.4026 $$	$$ 0.2454 $$	$$ 2.513 $$	$$ 1.947 $$	$$ 2.608 $$	$$ 0.8948 $$
GeMo$$ _3 $$	$$ 0.0401 $$	$$ 0.0 $$	$$ 0.0 $$	$$ 0.1894 $$	$$ 0.0473 $$	$$ 0.0325 $$	$$ 0.0 $$
Ca$$ _3 $$V	$$ 0.4592 $$	$$ 0.2048 $$	$$ 0.1149 $$	$$ 3.3111 $$	$$ 2.8356 $$	$$ 3.6542 $$	$$ 0.019 $$
Ga$$ _2 $$Te$$ _3 $$	$$ 2.0112 $$	$$ \times $$	$$ \times $$	$$ 53.3896 $$	$$ 4.6825 $$	$$ 4.8998 $$	$$ 1.7875 $$
CoAs$$ _2 $$	$$ 0.4629 $$	$$ 0.4389 $$	$$ 0.2684 $$	$$ 5.3617 $$	$$ 2.8407 $$	$$ 2.9208 $$	$$ 0.9943 $$
Li$$ _2 $$Al	$$ 30.7051 $$	$$ \times $$	$$ \times $$	$$ 61.9154 $$	$$ 3.9575 $$	$$ 4.8314 $$	$$ 2.1345 $$
VS	$$ 0.4204 $$	$$ 0.2477 $$	$$ 0.1806 $$	$$ 1.9372 $$	$$ 1.3665 $$	$$ 1.8303 $$	$$ 0.9189 $$
Ba$$ _2 $$Hg	$$ 5.206 $$	$$ \times $$	$$ \times $$	$$ 8.7511 $$	$$ 4.9936 $$	$$ 7.3342 $$	$$ 1.2468 $$
SrTiO$$ _3 $$	$$ 0.0185 $$	$$ 0.0 $$	$$ 0.0 $$	$$ 0.0934 $$	$$ 0.0374 $$	$$ 0.0271 $$	$$ 0.0 $$
Al$$ _2 $$FeCo	$$ 0.0098 $$	$$ 0.2357 $$	$$ 0.112 $$	$$ 0.137 $$	$$ 0.0685 $$	$$ 0.0658 $$	$$ 0.1755 $$
GaBN$$ _2 $$	$$ 0.0041 $$	$$ 0.3889 $$	$$ 0.289 $$	$$ 2.1663 $$	$$ 1.5589 $$	$$ 1.9171 $$	$$ 0.0455 $$
AcMnO$$ _3 $$	$$ 0.0385 $$	$$ 0.0 $$	$$ 0.0 $$	$$ 0.116 $$	$$ 0.0464 $$	$$ 0.0336 $$	$$ 0.0 $$
PaTlO$$ _3 $$	$$ 0.0136 $$	$$ 0.0 $$	$$ 0.0 $$	$$ 0.0924 $$	$$ 0.037 $$	$$ 0.0268 $$	$$ 0.0 $$
CdCuN	$$ 0.0031 $$	$$ 0.441 $$	$$ 0.4259 $$	$$ 2.7337 $$	$$ 2.9172 $$	$$ 2.2949 $$	$$ 0.0397 $$
HoHSe	$$ 0.0033 $$	$$ 0.3643 $$	$$ 0.3148 $$	$$ 2.859 $$	$$ 1.906 $$	$$ 1.9716 $$	$$ 0.0575 $$
Li$$ _2 $$ZnSi	$$ 25.3593 $$	$$ \times $$	$$ \times $$	$$ 34.3079 $$	$$ 2.9587 $$	$$ 4.104 $$	$$ 1.8731 $$
Cd$$ _2 $$AgPt	$$ 22.5447 $$	$$ \times $$	$$ \times $$	$$ 16.9997 $$	$$ 3.5895 $$	$$ 4.2417 $$	$$ 2.4137 $$
AlCrFe$$ _2 $$	$$ 0.6621 $$	$$ 0.2486 $$	$$ 0.1507 $$	$$ 3.6931 $$	$$ 2.2245 $$	$$ 2.2518 $$	$$ 0.7886 $$
ZnCdPt$$ _2 $$	$$ 0.0384 $$	$$ 0.4717 $$	$$ 0.4503 $$	$$ 3.2733 $$	$$ 3.5537 $$	$$ 2.0384 $$	$$ 0.0643 $$
EuAlSi	$$ 0.0495 $$	$$ 0.3849 $$	$$ 0.2963 $$	$$ 4.5051 $$	$$ 3.0034 $$	$$ 2.2451 $$	$$ 0.3419 $$
Sc$$ _3 $$TlC	$$ 0.0026 $$	$$ 0.0 $$	$$ 0.0 $$	$$ 0.0431 $$	$$ 0.0173 $$	$$ 0.0125 $$	$$ 0.0 $$
GaSeCl	$$ 23.3337 $$	$$ \times $$	$$ \times $$	$$ 38.0257 $$	$$ 8.615 $$	$$ 11.7449 $$	$$ 2.0172 $$
CaAgN	$$ 0.0064 $$	$$ 0.441 $$	$$ 0.4259 $$	$$ 3.6479 $$	$$ 3.1055 $$	$$ 2.4023 $$	$$ 0.0483 $$
BaAlGe	$$ 0.002 $$	$$ 0.4547 $$	$$ 0.3889 $$	$$ 3.0476 $$	$$ 1.6942 $$	$$ 2.5291 $$	$$ 0.0326 $$
K$$ _2 $$PdS$$ _2 $$	$$ 0.5466 $$	$$ 0.2467 $$	$$ 0.1377 $$	$$ 22.0109 $$	$$ 3.7687 $$	$$ 3.5226 $$	$$ 1.3316 $$
KCrO$$ _2 $$	$$ 0.0342 $$	$$ 0.2740 $$	$$ 0.1934 $$	$$ 2.5233 $$	$$ 1.9562 $$	$$ 1.8946 $$	$$ 0.6105 $$
TiZnCu$$ _2 $$	$$ 0.0188 $$	$$ 0.4083 $$	$$ 0.3344 $$	$$ 3.8363 $$	$$ 2.83 $$	$$ 1.609 $$	$$ 0.6861 $$
Ta$$ _2 $$N$$ _3 $$O	$$ 0.4603 $$	$$ 0.2357 $$	$$ 0.1111 $$	$$ 3.144 $$	$$ 2.3813 $$	$$ 1.4458 $$	$$ 0.7499 $$
AgBiSeS	$$ 0.0154 $$	$$ 0.0 $$	$$ 0.0 $$	$$ 0.1914 $$	$$ 0.0957 $$	$$ 0.0808 $$	$$ 0.1298 $$
ZrTaNO	$$ 0.0935 $$	$$ 0.5182 $$	$$ 0.5 $$	$$ 0.4704 $$	$$ 0.2352 $$	$$ 0.2191 $$	$$ 0.4131 $$
MnAlCuPd	$$ 0.0187 $$	$$ 0.1719 $$	$$ 0.0865 $$	$$ 3.3567 $$	$$ 2.3023 $$	$$ 2.219 $$	$$ 0.7371 $$
CsNaICl	$$ 0.0046 $$	$$ 0.5 $$	$$ 0.5 $$	$$ 0.1822 $$	$$ 0.0911 $$	$$ 0.0848 $$	$$ 0.1639 $$
DyThCN	$$ 0.0322 $$	$$ 0.4082 $$	$$ 0.3333 $$	$$ 0.1057 $$	$$ 0.0529 $$	$$ 0.0451 $$	$$ 0.0216 $$
Li$$ _2 $$MgCdP$$ _2 $$	$$ 39.8356 $$	$$ \times $$	$$ \times $$	$$ 36.702 $$	$$ 3.4202 $$	$$ 4.3517 $$	$$ 1.8915 $$
SrWNO$$ _2 $$	$$ 0.0378 $$	$$ 0.0 $$	$$ 0.0 $$	$$ 0.2707 $$	$$ 0.1083 $$	$$ 0.1001 $$	$$ 0.0867 $$
Sr$$ _2 $$BBrN$$ _2 $$	$$ 10.728 $$	$$ \times $$	$$ \times $$	$$ 34.7446 $$	$$ 2.9484 $$	$$ 4.7848 $$	$$ 1.0966 $$
ZrCuSiAs	$$ 0.1566 $$	$$ 0.2459 $$	$$ 0.1411 $$	$$ 5.63 $$	$$ 1.4075 $$	$$ 1.5158 $$	$$ 1.7131 $$
NdNiSnH$$ _2 $$	$$ 24.8101 $$	$$ 0.4252 $$	$$ 0.2993 $$	$$ 10.3403 $$	$$ 3.4393 $$	$$ 3.6793 $$	$$ 1.945 $$
MnCoSnRh	$$ 56.8397 $$	$$ \times $$	$$ \times $$	$$ 12.3179 $$	$$ 3.0676 $$	$$ 3.5955 $$	$$ 1.2971 $$
Mg$$ _2 $$ZnB$$ _2 $$Ir$$ _5 $$	$$ 6.8128 $$	$$ \times $$	$$ \times $$	$$ 60.6003 $$	$$ 6.7022 $$	$$ 7.5961 $$	$$ 1.5616 $$
AlCr4GaC2	$$ 0.0234 $$	$$ 0.5563 $$	$$ 0.3984 $$	$$ 4.9214 $$	$$ 2.4287 $$	$$ 1.7347 $$	$$ 0.0986 $$
Y$$ _3 $$Al$$ _3 $$NiGe$$ _2 $$	$$ 0.7301 $$	$$ 0.1035 $$	$$ 0.057 $$	$$ 4.0638 $$	$$ 3.1641 $$	$$ 2.9705 $$	$$ 0.5302 $$
Ba$$ _2 $$CeTaO$$ _6 $$	$$ 52.5924 $$	$$ \times $$	$$ \times $$	$$ 78.9662 $$	$$ 5.3529 $$	$$ 6.8904 $$	$$ 1.9963 $$

Performance comparison with GN-OA

As reported in ref^[36], the GN-OA algorithm achieved the highest performance when utilizing BO^[69] as the optimization algorithm and the MEGNet neural network model as the formation energy predictor to guide the optimization process (default GN-OA). Based on the data presented in Table 2, we observed that GN-OA showed a significantly lower success rate than that of ParetoCSP. In comparison to ParetoCSP, GN-OA achieved an accuracy of only $$ 50\% $$ ($$ 10 $$ out of $$ 20 $$ crystals) in predicting structures of binary crystals, whereas ParetoCSP achieved $$ 85\% $$ accuracy. For ternary crystals, GN-OA achieved a success rate of $$ 30\% $$ ($$ 6 $$ out of $$ 20 $$ crystals) compared to ParetoCSP's $$ 80\% $$. In the case of quarternary crystals, GN-OA did not achieve a single success, whereas ParetoCSP achieved a success rate of $$ 53.333\% $$. Overall, the success rate of GN-OA was only $$ 29.091\% $$, which is approximately $$ 2.562 $$ times lower than the accuracy achieved by ParetoCSP. Moreover, GN-OA could not predict any structure that ParetoCSP could not predict. These clearly establish the dominance of ParetoCSP over GN-OA, highlighting the higher quality of structure searching provided by AFPO-based GA compared to BO and the effectiveness of M3GNet IAP-based final energy prediction compared to MEGNet's formation energy prediction.

To understand the deteriorated performance of GN-OA in our benchmark study, firstly, we found that the CSP experiments conducted in the original study of GN-OA^[36] primarily focused on small binary crystals, particularly those with a $$ 1 $$: $$ 1 $$ atoms ratio. Secondly, a majority of these binary crystals belonged to four groups, namely oxide, sulfide, chloride, and fluoride, which demonstrates the lack of diversity in the GN-OA's benchmark set [Supplementary Figure 1B]. Moreover, most of the crystals examined had the cubic crystal system (mostly belonging to the $$ Fm-3m $$ space group). It merely explored other crystal systems or space groups. This choice of test structures for experimentation was insufficient in terms of CSP where only a few crystals possess all these specific properties. A more thorough exploration of diverse crystal systems and space groups was necessary to demonstrate the CSP performance of GN-OA. Our study effectively demonstrated that the optimization algorithms used in GN-OA are inadequate for predicting more complex crystals (such as quarternary crystals). Furthermore, our empirical findings highlighted the shortcomings of using MEGNet as a formation energy predictor in guiding the optimization algorithm toward the optimal crystal structures. In summary, we established that ParetoCSP outperformed GN-OA by achieving a staggering $$ 256.2\% $$ higher performance in terms of success rates than that of GN-OA, and the AFPO-based multi-objective GA proved to be a much better structure search algorithm than BO. Additionally, M3GNet IAP provided more accurate energy estimations for effective CSP compared to the MEGNet used in GN-OA. ParetoCSP also performs a further structure refinement using M3GNet IAP after obtaining the final optimized structure from the GA, which contributed to its higher accuracy compared to GN-OA where this is entirely absent.

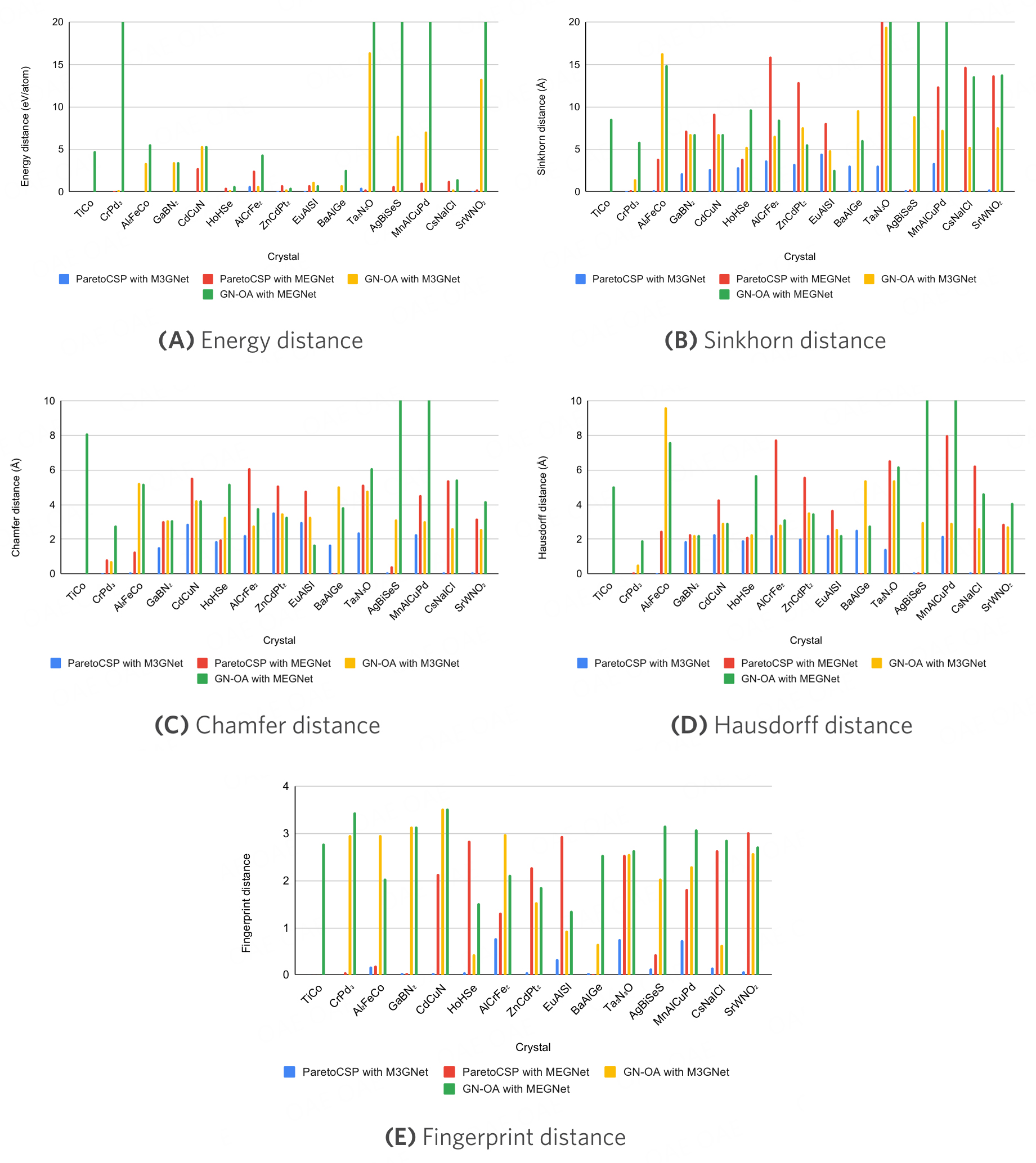
Figure 3 shows a performance metric value comparison for some sample crystals. For better visualization, we limited the $$ y $$-axis values to $$ 20 $$ for Figure 3A and B, and to $$ 10 $$ for Figure 3C and D. We found that the default ParetoCSP with M3GNet achieved lower (better) performance metric values for all the chosen sample crystals in terms of the metrics of ED, HD, and FP and for the majority of the cases for SD, and CD, compared to the default GN-OA. For some crystals (e.g., Ta$$ _2 $$N$$ _3 $$O, AgBiSeS, MnAlCuPd, SrWNO$$ _2 $$), the differences in the performance metric quantities are huge, indicating ParetoCSP's strong dominance over the default GN-OA.

Figure 3. Performance metric comparison of different CSP algorithms evaluated over the sample benchmark crystals. The metric values of ParetoCSP with M3GNet are much smaller (better) than those of other baseline algorithms, which quantitatively shows its superiority. In most cases, GN-OA with MEGNet's metric values is the highest (worst) which is aligned with the observation that it demonstrated the poorest performance among all CSP algorithms.

As discussed in the previous section, M3GNet universal IAP proved to be a better energy predictor than MEGNet. To fairly and objectively evaluate and compare our algorithm's performance, we replaced ParetoCSP's final energy calculator (M3GNet) with the MEGNet GNN for formation energy evaluation. Subsequently, we also replace MEGNet with M3GNet in GN-OA to show that the M3GNet IAP performs better than MEGNet for predicting the most stable energy for CSP. As a result, we ran experiments on four algorithms - ParetoCSP with M3GNet (default ParetoCSP), ParetoCSP with MEGNet, GN-OA with MEGNet (default GN-OA), and GN-OA with M3GNet.

The results of ParetoCSP with M3GNet have been discussed in detail in Section 3.2. ParetoCSP with MEGNet outperformed the default GN-OA by a factor of $$ \approx 1.31 $$ in terms of exact structure prediction accuracy. Individually, ParetoCSP with MEGNet achieved $$ 60\% $$ ($$ 12 $$ out of $$ 20 $$), $$ 40\% $$ ($$ 8 $$ out of $$ 20 $$), and $$ 13.333\% $$ ($$ 2 $$ out of $$ 15 $$) accuracy in predicting structures of binary, ternary, and quarternary crystals, respectively. In comparison, GN-OA with MEGNet achieved accuracies of $$ 50\% $$, $$ 30\% $$, and $$ 0\% $$ for binary, ternary, and quarternary crystals, respectively. This comparison clearly demonstrated that the AFPO-based GA is a more effective structure search method than BO. NiS$$ _2 $$ and EuAlSi are the only two crystals (both hexagonal) that GN-OA with MEGNet could predict the exact structures of but ParetoCSP with MEGNet could not. However, the opposite is true for $$ 8 $$ crystals including GaNi$$ _3 $$, GaBN$$ _2 $$, BaAlGe, AgBiSeS, etc., predominantly belonging to the tetragonal crystal system. Additionally, ParetoCSP with MEGNet was not successful in predicting any structure that ParetoCSP with M3GNet could not, strongly indicating the necessity for M3GNet as the energy predicting function (outperformed ParetoCSP with MEGNet by a factor of $$ \approx 1.86 $$). From Figure 3, we can see that ParetoCSP with M3GNet achieved much lower performance metric values than ParetoCSP with MEGNet for the majority of the cases, indicating its better prediction caliber.

Performance comparison of CSP algorithms with different energy models

As discussed in the previous section, M3GNet universal IAP proved to be a better energy predictor than MEGNet. To fairly and objectively evaluate and compare our algorithm's performance, we replaced ParetoCSP's final energy calculator (M3GNet) with the MEGNet GNN for formation energy evaluation. Subsequently, we also replace MEGNet with M3GNet in GN-OA to show that the M3GNet IAP performs better than MEGNet for predicting the most stable energy for CSP. As a result, we ran experiments on four algorithms - ParetoCSP with M3GNet (default ParetoCSP), ParetoCSP with MEGNet, GN-OA with MEGNet (default GN-OA), and GN-OA with M3GNet.

The results of ParetoCSP with M3GNet have been discussed in detail in Section 3.2. ParetoCSP with MEGNet outperformed the default GN-OA by a factor of $$ \approx 1.31 $$ in terms of exact structure prediction accuracy. Individually, ParetoCSP with MEGNet achieved $$ 60\% $$ ($$ 12 $$ out of $$ 20 $$), $$ 40\% $$ ($$ 8 $$ out of $$ 20 $$), and $$ 13.333\% $$ ($$ 2 $$ out of $$ 15 $$) accuracy in predicting structures of binary, ternary, and quarternary crystals, respectively. In comparison, GN-OA with MEGNet achieved accuracies of $$ 50\% $$, $$ 30\% $$, and $$ 0\% $$ for binary, ternary, and quarternary crystals, respectively. This comparison clearly demonstrated that the AFPO-based GA is a more effective structure search method than BO. NiS$$ _2 $$ and EuAlSi are the only two crystals (both hexagonal) that GN-OA with MEGNet could predict the exact structures of but ParetoCSP with MEGNet could not. However, the opposite is true for $$ 8 $$ crystals including GaNi$$ _3 $$, GaBN$$ _2 $$, BaAlGe, AgBiSeS, etc., predominantly belonging to the tetragonal crystal system. Additionally, ParetoCSP with MEGNet was not successful in predicting any structure that ParetoCSP with M3GNet could not, strongly indicating the necessity for M3GNet as the energy predicting function (outperformed ParetoCSP with MEGNet by a factor of $$ \approx 1.86 $$). From Figure 3, we can see that ParetoCSP with M3GNet achieved much lower performance metric values than ParetoCSP with MEGNet for the majority of the cases, indicating its better prediction caliber.

Based on the analysis conducted so far, two hypotheses were formulated: firstly, that GN-OA with M3GNet would outperform the default GN-OA, and secondly, that ParetoCSP with M3GNet would outperform GN-OA with M3GNet. As anticipated, GN-OA with M3GNet outperformed the default GN-OA (by a factor of $$ \approx 1.5 $$), again demonstrating M3GNet IAP as a much better energy model than MEGNet. For binary, ternary, and quarternary crystals, respectively, GN-OA with M3GNet (GN-OA with MEGNet) achieved $$ 60\% $$ ($$ 50\% $$), $$ 35\% $$ ($$ 30\% $$), and $$ 13.333\% $$ ($$ 0\% $$), respectively. Moreover, the default GN-OA did not achieve superiority over GN-OA with MEGNet on any chosen crystal, but the opposite is true for $$ 8 $$ crystals including TiCo, VS, HoHSe, CsNaICl, etc., and a majority of them belongs to the hexagonal crystal system. However, despite the improved performance of GN-OA with M3GNet, its efficiency still fell short in comparison to ParetoCSP with M3GNet due to the more effective structure search function of the latter, proving both hypotheses true. ParetoCSP with M3GNet outperformed GN-OA with M3GNet by a factor of $$ \approx 1.71 $$. Furthermore, the default ParetoCSP accurately predicted every structure that GN-OA with M3GNet successfully predicted. Again, from Figure 3, we can see that ParetoCSP with M3GNet achieved smaller performance metric values than GN-OA with M3GNet for the majority of the crystals. In fact, for some crystals such as Al$$ _2 $$FeCo, Ta$$ _2 $$N$$ _3 $$O, AgBiSeS, and SrWNO$$ _2 $$, the differences of metric values are enormous. To report the final outcomes, ParetoCSP with M3GNet outperformed all algorithms ($$ \approx 1.71\times $$ the second best, and $$ \approx 1.86\times $$ the third best). GN-OA with M3GNet ranked second best, exceeding the performance of the third best ParetoCSP with MEGNet by a small margin (by a factor of $$ \approx 1.09 $$). The default GN-OA demonstrated the lowest performance compared to all other algorithms.

Parametric study of ParetoCSP

As a multi-objective GA, several hyper-parameters are set before running our ParetoCSP algorithm for CSP. Here, we conducted experiments with our ParetoCSP algorithm with different parameter settings to evaluate their effect. We selected eight crystals for this study containing both successful and unsuccessful predictions, namely TiCo, Ba$$ _2 $$Hg, HoHSe, Cd$$ _2 $$AgPt, SrTiO$$ _3 $$, GaBN$$ _2 $$, MnAlCuPd, and AgBiSeS. The hyper-parameters chosen for the study include population size, crossover probability, mutation probability, and total number of generations used. The default parameter set is mentioned in Supplementary Note 1. All the performance results are presented in Table 4.

Table 4

Performance results with different hyper-parameters of ParetoCSP with M3GNet

	TiCo	Ba$$ _2 $$Hg	HoHSe	Cd$$ _2 $$AgPt	SrTiO$$ _3 $$	GaBN$$ _2 $$	MnAlCuPd	AgBiSeS
Pop, CP, MP, and Gen denote population size, crossover probability, mutation probability, and total number of generations, respectively. The best results are achieved for a population size of $$100$$, a crossover probability of $$0.8$$, a mutation probability of $$0.01$$, and a generation number $$\geq 1, 000$$. ParetoCSP failed to identify exact structures of Ba$$_2$$Hg and Cd$$_2$$AgPt for all parameter settings tested in this experiment. Pop: Population; CP: crossover probability; MP: mutation probability.
Pop $$ 30 $$	✘	✘	✘	✘	✔	✘	✘	✘
Pop $$ 60 $$	✔	✘	✔	✘	✔	✘	✘	✔
Pop $$ 100 $$	✔	✘	✔	✘	✔	✔	✔	✔
Pop $$ 200 $$	✔	✘	✔	✘	✔	✘	✘	✔
Pop $$ 300 $$	✔	✘	✔	✘	✔	✘	✔	✘
CP $$ 0.1 $$	✔	✘	✔	✘	✔	✘	✘	✘
CP $$ 0.2 $$	✔	✘	✔	✘	✔	✘	✘	✔
CP $$ 0.4 $$	✔	✘	✔	✘	✔	✘	✘	✔
CP $$ 0.6 $$	✔	✘	✔	✘	✔	✔	✘	✔
CP $$ 0.8 $$	✔	✘	✔	✘	✔	✔	✔	✔
MP $$ 0.0001 $$	✔	✘	✔	✘	✔	✘	✘	✘
MP $$ 0.001 $$	✔	✘	✔	✘	✔	✘	✘	✘
MP $$ 0.01 $$	✔	✘	✔	✘	✔	✔	✔	✔
MP $$ 0.1 $$	✔	✘	✔	✘	✔	✔	✘	✘
MP $$ 0.5 $$	✔	✘	✔	✘	✔	✔	✘	✘
Gen $$ 250 $$	✔	✘	✔	✘	✔	✘	✔	✘
Gen $$ 500 $$	✔	✘	✔	✘	✔	✔	✔	✘
Gen $$ 1, 000 $$	✔	✘	✔	✘	✔	✔	✔	✔
Gen $$ 2, 000 $$	✔	✘	✔	✘	✔	✔	✔	✔
Gen $$ 5, 000 $$	✔	✘	✔	✘	✔	✔	✔	✔

First, we examined the effect of different population sizes on the selected crystals. We ran the experiments with five different population sizes. The results in Table 4 show that our algorithm performed best with a population size of $$ 100 $$. Conversely, it could not accurately predict the structures of any crystal with a population size of $$ 30 $$, except for SrTiO$$ _3 $$. ParetoCSP consistently performed poorly for Ba$$ _2 $$Hg and Cd$$ _2 $$AgPt with every population size, while the results of SrTiO$$ _3 $$ showed the opposite trend.

Second, we analyzed the performance of our algorithm with varying crossover probabilities. The results indicated that the best performance was achieved with a probability of $$ 0.8 $$, and this was the only probability for which ParetoCSP identified the exact structure of MnAlCuPd. Except for GaBN$$ _2 $$ and AgBiSeS, for all five other crystals, ParetoCSP showed consistent performance with other crossover probabilities. We observed that our algorithm performed well with higher crossover probabilities for GaBN$$ _2 $$ and poorly for AgBiSeS with probability $$ < 0.2 $$.

Next, we evaluated ParetoCSP's performance with different mutation probabilities and observed that ParetoCSP performed best with a mutation probability of $$ 0.01 $$. Only MnAlCuPd and AgBiSeS had their exact structure successfully predicted with this mutation probability, while for other crystals except GaBN$$ _2 $$, ParetoCSP performed consistently with other probabilities. Our algorithm successfully predicted the structure of GaBN$$ _2 $$ for mutation probabilities $$ \geq 0.01 $$.

Finally, we ran experiments with different generations to investigate the impact on algorithm performance. In ref^[36], all experiments were run for $$ 5000 $$ steps for the BO. However, our results from Table 4 showed that $$ 1, 000 $$ generations were sufficient for ParetoCSP to achieve the optimal results for all $$ 8 $$ crystals. Except for GaBN$$ _2 $$ and AgBiSeS, for all five other crystals, ParetoCSP achieved optimal solutions within $$ 250 $$ generations. We would like to mention that we did not evaluate for $$ < 250 $$ generations, so it is possible that ParetoCSP could perform optimally for these crystals even with a smaller number of generations. None of the above-mentioned hyper-parameters could accurately predict the ground truth structures of Ba$$ _2 $$Hg and Cd$$ _2 $$AgPt.

Failure case study

ParetoCSP successfully predicted the structures for $$ 41 $$ out of $$ 55 $$ benchmark crystals in this research. Here, we conducted a further thorough investigation of the $$ 14 $$ unsuccessful predictions. For this, we calculated performance metric values of these $$ 14 $$ structures for all four algorithms discussed in this paper and then experimentally showed the output quality of each algorithm. We excluded the W$$ _{rmse} $$ and W$$ _{mae} $$ for this study as all four algorithms failed to predict these structures accurately. The results are presented in Figure 4 (only two of them are shown here in the main text, and the rest are shown in the Supplementary Materials).

Figure 4. Performance metric comparison of structure prediction of different algorithms for the 14 failure cases of ParetoCSP with M3GNet. Despite being inaccurate, ParetoCSP with M3GNet generated structures closer to the corresponding ground truth structures than any other algorithms.

The comparison results for energy distance metric (ED) are presented in Supplementary Figure 2A. We limited the $$ y $$-axis value to $$ 80 $$ for better visualization. ParetoCSP with M3GNet dominated all other algorithms for ED, achieving the lowest errors for $$ 9 $$ out of $$ 14 $$ crystals. ED is related to the final energy difference between the ground truth and the predicted structure, indicating that predicted structures by ParetoCSP are energetically closer to the energy of target structures than those by other algorithms. The only failure case where the ParetoCSP had the highest ED value among all algorithms was Li$$ _2 $$Al. The three performance metrics, SD, CD, and HD, are all related to the atomic sites of the ground truth and predicted crystal. ParetoCSP with M3GNet again outperformed all other algorithms, achieving the lowest distance scores for a majority of the failure cases, suggesting that the structures predicted by the ParetoCSP algorithms have the closest atomic site configurations compared to the target structures among all algorithms. We presented the results in Supplementary Figure 2B and C, and Figure 4A, respectively, with the $$ y $$-axis of Supplementary Figure 2B limited to $$ 200 $$ for visualization purposes. Finally, for the FP metric, which is related to the crystal atomic site FP, ParetoCSP with M3GNet achieved the lowest distance errors for $$ 11 $$ out of $$ 14 $$ crystals among all algorithms, proving better atomic site prediction quality. The results are shown in Figure 4B. Li$$ _2 $$Al again is the only crystal where the default ParetoCSP's FP value is the highest among all.

The observation that Li$$ _2 $$Al had the highest ED and FP values for ParetoCSP suggests that the combination of AFPO-based GA and M3GNet might not be the optimal choice for predicting this crystal. On the contrary, ParetoCSP with M3GNet achieved $$ 4 $$ out of $$ 5 $$, or $$ 5 $$ out of $$ 5 $$ lowest performance metric values for Ga$$ _2 $$Te$$ _3 $$, K$$ _2 $$PdS$$ _2 $$, Sr$$ _2 $$BBrN$$ _2 $$, ZrCuSiAs, MnCoSnRh, and Ba$$ _2 $$CeTaO$$ _6 $$, indicating that we are on the right track to predict structures of these crystals. In summary, each of the performance metrics is related to some specific features of the ground truth crystals, and ParetoCSP with M3GNet outperforms all other algorithms, which indicates that it predicts structures with better quality (closer to the ground truth structures) than other algorithms despite none of them are exact solutions.

Structures of the failed predictions are presented in Supplementary Figure 7. Taking a closer look at the predicted structures, we can clearly notice that, with the exception of some crystals, all of the predictions have the wrong crystal system. Moreover, none of the predicted crystals have the same space group as their corresponding ground truth space group. Furthermore, all the predicted structures deviate significantly from any unstable phase of the same crystal which indicates that the trajectories of the predicted structures by our algorithm did not lead to the right track to find the ground truth crystal, and methods to detect these wrong trajectories in advance needs to be added for better prediction quality.

Trajectory study

To further understand why ParetoCSP works better than GN-OA algorithm, we utilized the multi-dimensional performance metrics of CSP ^[47] to examine the search patterns of both optimization algorithms employed in ParetoCSP and GN-OA. For most of the crystals, the number of valid structures generated by ParetoCSP is enormous. For better visualization, we selected six crystals for this study which had a comparatively smaller number of valid structures: SrTiO$$ _3 $$, MnAlCuPd, GaNi$$ _3 $$, Al$$ _2 $$FeCo, Sc$$ _3 $$TlC, and SrWNO$$ _2 $$. ParetoCSP predicted exact structures of all these crystals, whereas GN-OA failed to predict the structures of MnAlCuPd, Al$$ _2 $$FeCo, and SrWNO$$ _2 $$. We used a population size of $$ 100 $$ and a total of $$ 250 $$ generations for ParetoCSP. For comparing fairly, we ran a total of $$ 15, 000 $$ steps with both GN-OA with MEGNet and M3GNet (GN-OA stopped making progress after $$ 5, 000 $$ steps for all of our targets). To analyze the structure search process, we computed the distance metrics between the valid structures and the ground truth structure. These distance features were then mapped into two-dimensional points using t-SNE ^[70]. The purpose of t-SNE is to map data points from a higher-dimensional space to a lower-dimensional space, typically 2D or 3D, while preserving the pairwise distances between the points. The intuition is that data points that are closer to each other in the higher dimension will remain close to each other after the mapping to the lower dimension. Subsequently, we visualized the trajectories of the structures during the search by connecting consecutive points if the latter structure had a lower energy than the former one. We presented the trajectories for SrTiO$$ _3 $$ and MnAlCuPd in Figure 5, and the rest are shown in Supplemental Figure 3 (see Supplementary Figures 4 and 5 for trajectory figures without arrows for better visualization of structure mapping). The initial points are represented by green triangles, while the ground truth structures are denoted by red stars. First, the distributions of the generated valid structures over the search by ParetoCSP and GN-OA are very different (Figure 5A and Dvs. Figure 5B and C, E and F). Distributions of ParetoCSP are much more diverse while the generated structures of GN-OA tend to be located in a shallow region [Figure 5G], indicating that the algorithm can only generate valid structures in a focused path. This is presumably due to the single point search characteristic of the BO algorithm. While a focused search is good when the direction is correct, it runs a high risk of getting trapped in the channeled path and thus loses its structure search capability. These assumptions become more visible from closely looking at Figures 5 G and H where t-SNE for all three algorithms are drawn in the same figure (see Supplementary Figure 6 for combined t-SNE for other chosen crystals). We can see that points generated by ParetoCSP are more spread out and have more diverse search directions than other algorithms, which ensures its higher structure search performance. This may explain ParetoCSP's success and GN-OA's failure in predicting structures of MnAlCuPd, Al$$ _2 $$FeCo, and SrWNO$$ _2 $$.

Figure 5. Trajectories of the traversed structure during the search of different CSP algorithms. (A-C) show the trajectory for SrTiO$$ _3 $$; and (D-F) show the trajectory for MnAlCuPd. The trajectories were drawn by calculating the distance metrics for the valid structures during the search and mapping them into $$ 2 $$D space using t-distributed stochastic neighbor embedding (t-SNE). Two consecutive points were connected if the latter structure had a lower energy than the former one; (G) and (H) show the t-SNE for all three algorithms in the same figure for SrTiO$$ _3 $$ and MnAlCuPd, respectively. The initial and optimal structures for all algorithms are marked with various colors and shapes. The points in ParetoCSP's trajectory are more spread out and have more diverse search directions than the other algorithms.

Another way to understand the structure search efficiency of ParetoCSP and GN-OA is to check the number of valid structures during the search process. ParetoCSP generated $$ 2, 492 $$, $$ 1, 518 $$, $$ 2, 248 $$, $$ 2, 873 $$, $$ 1, 843 $$, and $$ 1, 633 $$ valid structures in predicting SrTiO$$ _3 $$, MnAlCuPd, GaNi$$ _3 $$, Al$$ _2 $$FeCo, Sc$$ _3 $$TlC, and SrWNO$$ _2 $$, respectively, while the original GN-OA with MEGNet generated only $$ 1, 003 $$, $$ 681 $$, $$ 1, 701 $$, $$ 1, 350 $$, $$ 1, 499 $$, and $$ 1, 066 $$ valid structures for the same three targets, respectively. GN-OA with M3GNet, instead, generated a little bit more valid structures for SrTiO$$ _3 $$ (1, 049), GaNi$$ _3 $$ (2, 044), and Al$$ _2 $$FeCo (1, 475) but fewer for MnAlCuPd ($$ 569 $$), Sc$$ _3 $$TlC ($$ 1, 165 $$), and SrWNO$$ _2 $$ ($$ 955 $$). The number of valid structures generated by both GN-OA algorithms is significantly smaller compared to those of our ParetoCSP, indicating that the superiority of ParetoCSP may lie in its capability to make effective searches by generating more valid structures. The findings of ref^[36] showed that our ParetoCSP's AFPO-based GA search function performed much better than BO. Overall, GN-OA struggled to generate valid structures during the search process and wasted a majority of the search dealing with invalid structures. Moreover, the higher percentage of valid structures generated and more diverse search functions of ParetoCSP may have contributed to its higher probability of finding the exact structures.

DISCUSSION

We present ParetoCSP, a CSP algorithm that combines an AFPO enhanced multi-objective GA as an effective structure search function and M3GNet universal IAP as a constructive final energy predictor to achieve efficient structure search for CSP. The objective is to effectively capture the complex relationships between atomic configurations and their corresponding energies. Firstly, ParetoCSP uses the age of a population as a separate optimization criterion. This leads the algorithm to treat the age as a separate dimension in the multi-objective Pareto front where the GA aims to generate structures to minimize the final energy per atom, as well as having low genotypic age. The finding of ref^[59] provides a more extensive search process which enables the NSGA-III to perform better as shown in the trajectory results in Section 3.7, where we see that ParetoCSP generated a lot more valid structures during the search process than other evaluated CSP algorithms. This demonstrates the effective exploration of the crystal structure space by ParetoCSP and the efficient identification of the most stable structures.

Overall, we found that ParetoCSP remarkably outperforms the GN-OA algorithm by a factor of $$ 2.562 $$ and overall achieved $$ 74.55\% $$ accuracy. The comprehensive experimentation was carried out on $$ 55 $$ benchmark sets consisting of diverse space groups, which shows that the algorithm can efficiently handle a wide range of crystal systems, including complex ternary and quarternary compounds, whereas GN-OA performed poorly on the quarternary crystals, and most of the ternary crystals. Moreover, a majority of them belongs to the cubic crystals system, proving GN-OA's lack of capability of exploring the structure space of diverse crystal systems. However, all the algorithms show poor performance for crystals belonging to the orthorhombic and monoclinic crystal systems. This performance limits of ParetoCSP can be attributed to either the optimization algorithm or the ML potential.

First, we found that for both ParetoCSP and GN-OA, the search process tends to generate a majority of invalid structures even though ParetoCSP works much better than GN-OA. These invalid structures are a waste of search time. Better algorithms that consider crystal symmetry or data-driven generative models may be developed to improve the percentage of valid structures and increase the search efficiency during the search process. In ParetoCSP, the M3GNet IAP is used as the final energy predictor during the search process and structure relaxer after finishing the search process. Compared to MEGNet, M3GNet IAP is proven to be a better choice since after replacing GN-OA's MEGNet with M3GNet IAP, its performance can be improved by a factor of $$ 1.5 $$. Overall, our results suggest the importance of developing stronger universal ML potentials in modern CSP algorithm development. Other IAP models such as TeaNet ^[50] can be experimented with to check whether better performance can be achieved with ParetoCSP and can be compared to the results with M3GNet. Unlike GN-OA, ParetoCSP performs a further refinement of the output structure which helped generate exact structures. We used M3GNet IAP for the structure relaxation. More advanced structure relaxation methods can be tested instead to get better performance.

For the first time, we have used a set of seven quantitative performance metrics to compare and investigate algorithm performances of ParetoCSP and the baselines. We can see from Table 3 that each of the unsuccessful predictions had at least one of the performance metrics value larger than the ground truth value. Additionally, Figure 3 shows that ParetoCSP with M3GNet generated better solutions than any other baseline CSP algorithms as they had much lower performance metric distances (errors) than others. Furthermore, the performance metrics also show that even though ParetoCSP was unable to predict $$ 14 $$ crystal structures, it still produced better quality structures compared to other CSP algorithms. These metrics can also be used to show, for a specific crystal, whether the algorithm is on the right track to predict its structure or not.

Inspired by the great success of AlphaFold2 ^[45] for protein structure prediction, which does not rely on first-principles calculations, we believe that data-driven CSP algorithms based on ML deep neural network energy models have big potential and can reach the same level as AlphaFold2. For this reason, we have focused on the performance comparison with the SOTA GN-OA, a ML potential-based CSP algorithm, and we did not compare our results with CALYPSO ^[15] and USPEX ^[14], despite the fact that USPEX also utilizes evolutionary algorithms similar to ours. These algorithms are extremely slow and are not scalable to complex crystals as they depend on ab initio energy calculations, which are computationally very expensive and slow. Currently, they can only deal with simple chemical systems or relatively small crystals ($$ < 10 $$ atoms in the unit cell) which is a major disadvantage.

CONCLUSION

We have introduced an innovative CSP algorithm named ParetoCSP, which synergizes two key components: the multi-objective GA employing AFPO and the M3GNet IAP, for predicting the most stable crystalline material structures. The AFPO-based GA effectively functions as a structure search algorithm, complemented by the role of M3GNet IAP as an efficient final energy predictor that guides the search process. Through comprehensive experimentation involving $$ 55 $$ benchmark crystals, the potency of our algorithm has been demonstrated, notably surpassing GN-OA with MEGNet and GN-OA with M3GNet by substantial factors of $$ 2.562 $$ and $$ 1.71 $$, respectively. Utilizing benchmark performance metrics, we have provided an in-depth analysis of the quality of structures generated by our algorithm. Furthermore, we have quantitatively depicted deviations from the ground truth structure for failure cases across all algorithms, highlighting the superior performance of ParetoCSP in this aspect as well. By means of a trajectory analysis of the generated structures, we have established that ParetoCSP produces a greater percentage of valid structures compared to GN-OA during the search process due to its enhanced search algorithm. Given these significant advancements, we believe that ML potential-based CSP algorithms such as ParetoCSP hold immense promise for advancing the boundaries of CSP and facilitating the discovery of novel materials with desired properties.

DECLARATIONS

Authors' contributions

Conceptualization, resources, supervision, funding acquisition: Hu J

Methodology, writing - original draft preparation: Omee SS, Hu J, Wei L

Software: Omee SS, Hu J

Writing - review and editing: Omee SS, Hu J, Wei L, Hu M

Visualization: Omee SS

Availability of data and materials

The data that support the findings of this study are openly downloadable from the Materials Project database at https://www.materialsproject.org. The source code of our work is freely accessible at https://github.com/sadmanomee/ParetoCSP.

Financial support and sponsorship

The research reported in this work was supported in part by National Science Foundation under the grants 2110033, OAC-2311203, and 2320292. The views, perspectives, and content do not necessarily represent the official views of the NSF.

Conflicts of interest

All authors declared that there are no conflicts of interest.

Ethical approval and consent to participate

Not applicable.

Consent for publication

Not applicable.

Copyright

REFERENCES

1. Oganov AR, Glass CW. Crystal structure prediction using ab initio evolutionary techniques: principles and applications. J Chem Phys 2006;124:244704.

2. Oganov AR, Pickard CJ, Zhu Q, Needs RJ. Structure prediction drives materials discovery. Nat Rev Mater 2019;4:331-48.

3. Hu J, Yang W, Dong R, et al. Contact map based crystal structure prediction using global optimization. CrystEngComm 2021;23:1765-76.

4. Yin X, Gounaris CE. Search methods for inorganic materials crystal structure prediction. Curr Opin Chem Eng 2022;35:100726.

5. Brown N, Ertl P, Lewis R, Luksch T, Reker D, Schneider N. Artificial intelligence in chemistry and drug design. J Comput Aided Mol Des 2020;34:709-15.

6. Kvashnin AG, Allahyari Z, Oganov AR. Computational discovery of hard and superhard materials. J Appl Phys 2019;126:040901.

7. Noh J, Kim J, Stein HS, et al. Inverse design of solid-state materials via a continuous representation. Matter 2019;1:1370-84.

8. Kim B, Lee S, Kim J. Inverse design of porous materials using artificial neural networks. Sci Adv 2020;6:eaax9324.

9. Dan Y, Zhao Y, Li X, Li S, Hu M, Hu J. Generative adversarial networks (GAN) based efficient sampling of chemical composition space for inverse design of inorganic materials. npj Comput Mater 2020;6:84.

10. Long T, Fortunato NM, Opahle I, et al. Constrained crystals deep convolutional generative adversarial network for the inverse design of crystal structures. npj Comput Mater 2021;7:66.

11. Oviedo F, Ren Z, Sun S, et al. Fast and interpretable classification of small X-ray diffraction datasets using data augmentation and deep neural networks. npj Comput Mater 2019;5:60.

12. Pickard CJ, Needs RJ. Ab initio random structure searching. J Phys Condens Matter 2011;23:053201.

13. Woodley SM, Catlow R. Crystal structure prediction from first principles. Nat Mater 2008;7:937-46.

14. Glass CW, Oganov AR, Hansen N. USPEX - evolutionary crystal structure prediction. Comput Phys Commun 2006;175:713-20.

15. Wang Y, Lv J, Zhu L, Ma Y. CALYPSO: a method for crystal structure prediction. Comput Phys Commun 2012;183:2063-70.

16. Hohenberg P, Kohn W. Inhomogeneous electron gas. Phys Rev 1964;136:B864-71.

17. Sham LJ, Kohn W. One-particle properties of an inhomogeneous interacting electron gas. Phys Rev 1966;145:561-7.

18. Xie T, Grossman JC. Crystal graph convolutional neural networks for an accurate and interpretable prediction of material properties. Phys Rev Lett 2018;120:145301.

19. Chen C, Ye W, Zuo Y, Zheng C, Ong SP. Graph networks as a universal machine learning framework for molecules and crystals. Chem Mater 2019;31:3564-72.

20. Schütt KT, Sauceda HE, Kindermans PJ, Tkatchenko A, Müller KR. SchNet - a deep learning architecture for molecules and materials. J Chem Phys 2018;148:241722.

21. Park CW, Wolverton C. Developing an improved crystal graph convolutional neural network framework for accelerated materials discovery. Phys Rev Mater 2020;4:063801.

22. Omee SS, Louis SY, Fu N, et al. Scalable deeper graph neural networks for high-performance materials property prediction. Patterns 2022;3:100491.

23. Choudhary K, Decost B. Atomistic Line Graph Neural Network for improved materials property predictions. npj Comput Mater 2021;7:185.

24. Kirkpatrick S, Gelatt CD Jr, Vecchi MP. Optimization by simulated annealing. Science 1983;220:671-80.

25. Pannetier J, Bassas-Alsina J, Rodriguez-Carvajal J, Caignaert V. Prediction of crystal structures fromcrystal chemistry rules by simulated annealing. Nature 1990;346:343-5.

26. Schön JC, Jansen M. First step towards planning of syntheses in solid‐state chemistry: determination of promising structure candidates by global optimization. Angew Chem Int Ed Engl 1996;35:1286-304.

27. Ma Y, Eremets M, Oganov AR, et al. Transparent dense sodium. Nature 2009;458:182-5.

28. Martoňák R, Laio A, Bernasconi M, et al. Simulation of structural phase transitions by metadynamics. Z für Krist Cryst Mater 2009;458:182-5.

29. Wales DJ, Doye JPK. Global optimization by basin-hopping and the lowest energy structures of lennard-jones clusters containing up to 110 atoms. J Phys Chem A 1997;101:5111-6.

30. Wales DJ, Scheraga HA. Global optimization of clusters, crystals, and biomolecules. Science 1999;285:1368-72.

31. Goedecker S. Minima hopping: an efficient search method for the global minimum of the potential energy surface of complex molecular systems. J Chem Phys 2004;120:9911-7.

32. Smith RW. Energy minimization in binary alloy models via genetic algorithms. Phys Commun 1992;71:134-46.

33. Woodley SM, Battle PD, Gale JD, Catlow CRA. The prediction of inorganic crystal structures using a genetic algorithm and energy minimisation. Phys Chem Chem Phys 1999;1:2535-42.

34. Lyakhov AO, Oganov AR, Stokes HT, Zhu Q. New developments in evolutionary structure prediction algorithm USPEX. Comput Phys Commun 2013;184:1172-82.

35. Yamashita T, Sato N, Kino H, Miyake T, Tsuda K, Oguchi T. Crystal structure prediction accelerated by Bayesian optimization. Phys Rev Mater 2018;2:013803.

36. Cheng G, Gong XG, Yin WJ. Crystal structure prediction by combining graph network and optimization algorithm. Nat Commun 2022;13:1492.

37. Ryan K, Lengyel J, Shatruk M. Crystal structure prediction via deep learning. J Am Chem Soc 2018;140:10158-68.

38. Hu J, Zhao Y, Li Q, et al. Deep learning-based prediction of contact maps and crystal structures of inorganic materials. ACS Omega 2023;8:26170-9.

39. Kresse G, Furthmüller J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput Mater Sci 1996;6:15-50.

40. Soler JM, Artacho E, Gale JD, et al. The SIESTA method for ab initio order- N materials simulation. J Phys Condens Matter 2002;14:2745.

41. Hautier G, Fischer C, Ehrlacher V, Jain A, Ceder G. Data mined ionic substitutions for the discovery of new compounds. Inorg Chem 2011;50:656-63.

42. Wei L, Fu N, Siriwardane EMD, et al. TCSP: a template-based crystal structure prediction algorithm for materials discovery. Inorg Chem 2022;61:8431-9.

43. Kusaba M, Liu C, Yoshida R. Crystal structure prediction with machine learning-based element substitution. Comput Mater Sci 2022;211:111496.

44. Senior AW, Evans R, Jumper J, et al. Improved protein structure prediction using potentials from deep learning. Nature 2020;577:706-10.

45. Jumper J, Evans R, Pritzel A, et al. Highly accurate protein structure prediction with AlphaFold. Nature 2021;596:583-9.

46. Baek M, DiMaio F, Anishchenko I, et al. Accurate prediction of protein structures and interactions using a three-track neural network. Science 2021;373:871-6.

47. Wei L, Li Q, Omee SS, Hu J. Towards quantitative evaluation of crystal structure prediction performance. Comput Mater Sci 2024;235:112802.

48. Podryabinkin EV, Tikhonov EV, Shapeev AV, Oganov AR. Accelerating crystal structure prediction by machine-learning interatomic potentials with active learning. Phys Rev B 2019;99:064114.

49. Tong Q, Xue L, Lv J, Wang Y, Ma Y. Accelerating CALYPSO structure prediction by data-driven learning of a potential energy surface. Faraday Discuss 2018;211:31-43.

50. Takamoto S, Izumi S, Li J. TeaNet: Universal neural network interatomic potential inspired by iterative electronic relaxations. Comput Mater Sci 2022;207:111280.

51. Takamoto S, Shinagawa C, Motoki D, et al. Towards universal neural network potential for material discovery applicable to arbitrary combination of 45 elements. Nat Commun 2022;13:2991.

52. Choudhary K, Decost B, Major L, Butler K, Thiyagalingam J, Tavazza F. Unified graph neural network force-field for the periodic table: solid state applications. Digit Discov 2023;2:346-55.

53. Chen C, Ong SP. A universal graph deep learning interatomic potential for the periodic table. Nat Comput Sci 2022;2:718-28.

54. Deng B, Zhong P, Jun K, et al. CHGNet as a pretrained universal neural network potential for charge-informed atomistic modelling. Nat Mach Intell 2023;5:1031-41.

55. Shao X, Lv J, Liu P, et al. A symmetry-orientated divide-and-conquer method for crystal structure prediction. J Chem Phys 2022;156:014105.

56. Hahn T, Shmueli U, Arthur JCW. International tables for crystallography. 1983. Available from: https://it.iucr.org/. [Last accessed on 22 Feb 2024].

57. Deb K, Jain H. An evolutionary many-objective optimization algorithm using reference-point-based nondominated sorting approach, part Ⅰ: solving problems with box constraints. IEEE Trans Evol Computat 2014;18:577-601.

58. Jain H, Deb K. An evolutionary many-objective optimization algorithm using reference-point based nondominated sorting approach, part Ⅱ: handling constraints and extending to an adaptive approach. IEEE Trans Evol Computat 2014;18:602-22.

59. Schmidt MD, Lipson H. Age-fitness pareto optimization. In: Proceedings of the 12th Annual Conference on Genetic and Evolutionary Computation. New York, NY, USA: Association for Computing Machinery; 2010. pp. 543-4.

60. Isayev O, Oses C, Toher C, Gossett E, Curtarolo S, Tropsha A. Universal fragment descriptors for predicting properties of inorganic crystals. Nat Commun 2017;8:15679.

61. Cheng J, Zhang C, Dong L. A geometric-information-enhanced crystal graph network for predicting properties of materials. Commun Mater 2021;2:92.

62. Yan K, Liu Y, Lin Y, Ji S. Periodic graph transformers for crystal material property prediction. arXiv. [Preprint. ] Sep 23, 2022[accessed 2024 Feb 22]. Available from: https://arxiv.org/abs/2209.11807.

63. Hu J, Goodman E, Seo K, Fan Z, Rosenberg R. The hierarchical fair competition (HFC) framework for sustainable evolutionary algorithms. Evol Comput 2005;13:241-77.

64. Hornby GS. ALPS: the age-layered population structure for reducing the problem of premature convergence. In: Proceedings of the 8th Annual Conference on Genetic and Evolutionary Computation. New York, NY, USA: Association for Computing Machinery; 2006; pp. 815-22. 2006.

65. Schmidt M, Lipson H. Age-fitness pareto optimization. In: Riolo R, Mcconaghy T, Vladislavleva E, editors. Genetic programming theory and practice VⅢ. New York, NY, USA: Springer; 2011. pp. 129-46.

66. Deb K, Pratap A, Agarwal S, Meyarivan T. A fast and elitist multiobjective genetic algorithm: Nsga-Ⅱ. IEEE Trans Evol Comput 2002;6:182-97.

67. Blank J, Deb K, Roy PC. Investigating the normalization procedure of NSGA-Ⅲ. Available from: https://www.egr.msu.edu/~kdeb/papers/c2018009.pdf. [Last accessed on 25 Mar 2024]

68. Jain A, Ong SP, Hautier G, et al. Commentary: The materials project: a materials genome approach to accelerating materials innovation. APL Mater 2013;1:011002.

69. Bergstra J, Yamins D, Cox D. Making a science of model search: hyperparameter optimization in hundreds of dimensions for vision architectures. In: Proceedings of the 30th International Conference on Machine Learning. Atlanta, Georgia, USA: PMLR; 2013. pp. 115-23. Available from: https://proceedings.mlr.press/v28/bergstra13.html. [Last accessed on 22 Feb 2024].

70. van der Maaten L, Hinton G. Visualizing data using t-SNE. 2008. Available from: https://www.jmlr.org/papers/volume9/vandermaaten08a/vandermaaten08a.pdf. [Last accessed on 22 Feb 2024].

Cite This Article

Research Article

Open Access

Crystal structure prediction using neural network potential and age-fitness Pareto genetic algorithm

Sadman Sadeed Omee, ... Jianjun Hu

How to Cite

Omee, S. S.; Wei, L.; Hu, M.; Hu, J. Crystal structure prediction using neural network potential and age-fitness Pareto genetic algorithm. J. Mater. Inf. 2024, 4, 2. http://dx.doi.org/10.20517/jmi.2023.33

Download Citation

If you have the appropriate software installed, you can download article citation data to the citation manager of your choice. Simply select your manager software from the list below and click on download.

Export Citation File:

RIS BibTeX EndNote

Type of Import

Direct Import Indirect Import

Tips on Downloading Citation

This feature enables you to download the bibliographic information (also called citation data, header data, or metadata) for the articles on our site.

Citation Manager File Format

Use the radio buttons to choose how to format the bibliographic data you're harvesting. Several citation manager formats are available, including EndNote and BibTex.

Type of Import

If you have citation management software installed on your computer your Web browser should be able to import metadata directly into your reference database.

Direct Import: When the Direct Import option is selected (the default state), a dialogue box will give you the option to Save or Open the downloaded citation data. Choosing Open will either launch your citation manager or give you a choice of applications with which to use the metadata. The Save option saves the file locally for later use.

Indirect Import: When the Indirect Import option is selected, the metadata is displayed and may be copied and pasted as needed.

About This Article

Special Issue

This article belongs to the Special Issue Application of Machine Learning to Crystal Structure Prediction

Copyright

© The Author(s) 2024. Open Access This article is licensed under a Creative Commons Attribution 4.0 International License (https://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, sharing, adaptation, distribution and reproduction in any medium or format, for any purpose, even commercially, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.

Data & Comments

Data

Views

861

Downloads

234

Citations

3

Comments

0

4

Comments

Comments must be written in English. Spam, offensive content, impersonation, and private information will not be permitted. If any comment is reported and identified as inappropriate content by OAE staff, the comment will be removed without notice. If you have any queries or need any help, please contact us at support@oaepublish.com.

⁰

Download PDF

Download XML 5 downloads

Cite This Article 8 clicks

Export Citation 10 clicks

Like This Article 4 likes

Share This Article

https://www.oaepublish.com/articles/jmi.2023.33

Scan the QR code for reading!

See Updates

Contents

Figures

Crystal structure prediction using neural network potential and age-fitness Pareto genetic algorithm

Abstract

Keywords

INTRODUCTION

METHOD

ParetoCSP: algorithm description

AFPO

NSGA-III: multi-objective GA

M3GNet inter-atomic potential

Evaluation criteria

RESULTS

Benchmark set description

Performance analysis of ParetoCSP

Performance comparison with GN-OA

Performance comparison of CSP algorithms with different energy models

Parametric study of ParetoCSP

Failure case study

Trajectory study

DISCUSSION

CONCLUSION

DECLARATIONS

Authors' contributions

Availability of data and materials

Financial support and sponsorship

Conflicts of interest

Ethical approval and consent to participate

Consent for publication

Copyright

REFERENCES

Cite This Article

How to Cite

Download Citation

Export Citation File:

Type of Import

Tips on Downloading Citation

Citation Manager File Format

Type of Import

About This Article

Special Issue

Copyright

Data & Comments

Data

Comments

Share This Article

See Updates

Committee on Publication Ethics

Portico

Committee on Publication Ethics

Portico