Evolution of prehension ability in an anthropomorphic neurorobotic arm

In this paper, we show how a simulated anthropomorphic robotic arm controlled by an artificial neural network can develop effective reaching and grasping behaviour through a trial and error process in which the free parameters encode the control rules which regulate the fine-grained interaction between the robot and the environment and variations of the free parameters are retained or discarded on the basis of their effects at the level of the global behaviour exhibited by the robot situated in the environment. The obtained results demonstrate how the proposed methodology allows the robot to produce effective behaviours thanks to its ability to exploit the morphological properties of the robot's body (i.e. its anthropomorphic shape, the elastic properties of its muscle-like actuators and the compliance of its actuated joints) and the properties which arise from the physical interaction between the robot and the environment mediated by appropriate control rules.

Introduction

The control of arm and hand movements in human and nonhuman primates is a fundamental research topic in cognitive sciences, neurosciences and robotics. Within arm and hand control, reaching and grasping behaviours represent key abilities as they constitute a prerequisite for complex object manipulation and use. In cognitive sciences, experimental and modelling studies have demonstrated the strict interdependence between action control and other cognitive functions such as language (Cangelosi et al., 2005 ; Pulvermuller, 2005 ). For example, some theories of language evolution have focused on the relationship between hand use, tool making and language evolution (Corballis, 2003 ). In neuroscience, numerous studies have demonstrated the fundamental role of the mirror neuron systems for motor control and in general for cognitive processing (Gallese and Lakoff, 2005 ; Rizzolatti and Arbib, 1998 ). In robotics, the motor control of arm and hand is a paradigmatic example of the difficulties that arise in the reverse engineering problem and the use of bio-inspired techniques in intelligent systems design (Schaal, 2002 ).

Despite the importance of the topic, the large body of available behavioural and neuroscientific data, and the vast number of studies done, the issues of how primates and humans learn to display reaching and grasping behaviour still remains highly controversial (Schaal, 2002 ; Shadmehr, 2002 ). Moreover, whilst many of the aspects that make these problems difficult have been identified, experimental research based on different techniques does not seem to converge towards the identification of a general methodology for developing robots able to display effective reaching and grasping abilities.

In this respect, one of the most controversial contraposition is between internal models (Kawato, 2002 ; Wolpert and Flanagan, 2002 ) and equilibrium point approaches (Shadmehr, 2002 ). The former approach is based on the assumption that our brain possess an internal model which allow us to: (a) predict how our limb will move and the sensations which will arise given the current sensory state and given a certain motor command which is going to be executed (direct mapping, and (b) transform a desired sensory state into the corresponding motor command which will achieve it (inverse mapping). In contrast, the latter approach is based on the assumption that muscles and associated spinal reflex circuitry confer to our limbs the ability to passively settle into stable position (i.e. equilibrium points) independently from their previous position. According to this hypothesis, the role of the central nervous system simply consists in the modification of the current equilibrium point.

In this paper, we will show how a simulated anthropomorphic arm can develop reaching and grasping skills through an adaptive evolutionary process (Nolfi and Floreano, 2000a ) in which the free parameters regulate the fine-grained interactions between the robot and the environment and in which variations of free parameters are retained or discarded on the basis of their effects on the overall ability of the robot to reach and grasp objects. The analysis of the obtained results confirms the importance of dynamics resulting robot∕environmental interactions and from the use of muscle-like actuators. Moreover, the results obtained demonstrate that effective reaching and grasping skills can be developed without relying on internal models performing direct and inverse mappings.

We will first review current work on reaching, with a brief discussion of the main research issues in this field and a review of current literature on the adaptive design of arm control behaviour in cognitive robots. The robotic model experimental setup will be described in section Materials and Methods. Subsequently in section Results we describe the results obtained. Finally, in Discussion the significance of the results obtained and our plans for the future.

Research issues in reaching and grasping in primates and humans

The primate arms consist of three main segments: arm, forearm and hand. These are attached to previous segments (the shoulder) through three actuated joints: shoulder, elbow and wrist joints. Roughly speaking, human arms have seven limited degrees of freedom (DOFs): three in the shoulder, one at the elbow and three at the wrist (Jones and Lederman, 2006 ).

Anthropomorphic robotic arms typically consist of three segments connected through motorized joints. Some models use all the seven DOFs listed above, others may include only part of them. From the point of view of the control system, reaching consists in producing the appropriate sequence of motor actions (i.e. setting the appropriate torque force for each actuated joint) that, given the current state of the arm and given the current desired target point, will bring the endpoint of the arm in the current desired target position.

Various issues have been identified in the study of reaching behaviour in primates and humans. The main research questions related to robotics research include (i) the role of the redundancy of DOFs; (ii) the nonlinear relationship between joint movement and hand∕target position; (iii) the role of gravity and inertia in suspended arms; (iv) the effects of speed and noise in motor control signals. First, we need to consider that when the number of DOFs is redundant, as in the case of primate arms, there is an infinite number of trajectories and of final postures for reaching any given target point. This redundancy potentially allows anthropomorphic arms to reach a target point by circumventing obstacles or by overcoming problems due to the limits of the DOFs. However, the redundancy of DOFs also implies that the space to be searched during learning is rather vast, making learning very difficult.

The second issue regards the fact that anthropomorphic arms are highly nonlinear systems. Small variations in some of the joints might have a huge impact on the end-position of the arm. At the same time, significant variations of other joints might not have any impact. In addition, due to the limits on the joints DOFs and due to the interactions between joints, similar target positions might require rather different trajectories and final postures. At the same time, rather different target positions might require similar trajectories and final postures.

Gravity and physics dynamics also have a fundamental role in arm control. In articulated and suspended structures such as an anthropomorphic arm, gravity and inertia play a key role. In primate arms, muscles and associated spinal reflex circuitry appear to confer to the arm the ability to passively settle into a stable position (i.e. an equilibrium point) independently from its previous position. If this hypothesis is correct, the contribution of the central nervous system would simply consists in the modification of the current equilibrium point (Shadmehr, 2002 ).

Finally, the fact that sensors and actuators might be slow and noisy greatly affects the development of robotic arm. For instance, in humans the visual and proprioceptive information encoding changes of joints positions is available with a delay up to 100 ms. Motor commands issued by the central nervous system may take up to 50 ms to initiate muscle contraction (Mial, 2002 ). Moreover, sensors might provide only incomplete information (e.g. the target point might be partially or totally occluded by obstacles and by the arm).

Evolutionary robotics and neural network models of arm control

Evolutionary robotics consists on the autonomous design of the controller of robots through the use of evolutionary computation methods such as genetic algorithms (Nolfi and Floreano, 2000b ). Typically in evolutionary robotic experiments the researcher defines the body of a robot (joints, limbs, sensors) and the surrounding environment (objects, obstacles, physics dynamics) with which it will interact. The robot control system consists of artificial neural network which has to learn to map input signals into motor responses. Learning is achieved through the evolution of the neural network parameters (connection weights and∕or network topology).

Artificial neural networks have been typically used in robotics research to learn the correct mapping between two different spaces (e.g. joints, actuators, workspace; see (Torras, 2002 )) as in inverse dynamics methods based on internal model approaches. Instead in the evolutionary approach the neural controller is seen as an internal dynamical system that interacts with the environments via the agentquotidns body. There are not explicit mappings between spaces, but this emerges from minute continuous controller-body–environment interactions. From this point of view, the agentquotidns behaviour is an emergent property of those tiny interactions. The evolutionary process is able to exploit the potential of simple architectures via dynamical interaction and is likely to lead to complex adaptive behaviour starting from minimal agents.

Notwithstanding the fact that evolution process leads to the selection and design of neural networks able to accomplish some task, this process is not a correlation-learning procedure, neither error-miniziming learning, nor a reinforcement-based procedure. Evolutionary robotics directly deals with some of the weakness of inverse dynamics approaches. In particular, it has been shown that an accurate mapping for inverse kinematics using feed-forward neural networks, due to global effect of weights, is extremely difficult to achieve (Krose and Van der smagt, 1993 ; Torras, 2002 ). In the evolutionary approach, as the controller is a dynamical system that acts directly and continuosly onto the dynamic of agent∕environment interaction, it is possible to exploit simple architecture, such as multi-layer perceptrons, to learn inverse kinematic-dinamic solutions (Bianco and Nolfi, 2004 ; Massera et al., 2006 ). Furthermore, with the evolutionary paradigm there is no need to specify exactly the desired output, as in error-minimizing learning. This allows us to tackle the inverse dynamic problem for redundant anthropomorphic arm. In fact, in supervised approach for a given input the controller has to generate a sequence of forces to apply that are difficult to calculate ‘a-priori’ and to learn by error-minimizing procedures or reinforcement learning.

There are also situations where the same sensory pattern requires different responses of the robotic agent such as sensory aliasing (Nolfi and Marocco, 2001 ). This is a major issue in neural network correlation-based learning such as Hebbian rule or self-organizing maps. Instead, in evolutionary robotics the neural controller does not have to learn to follow a predefined pathway and can explore different solutions to achieve the same target points in space.

There have been few previous attempts to use evolutionary techniques to develop the controller for a robotic arm. Bianco and Nolfi (2004) used a standard evolutionary robotics approach for the autonomous design of the neural controller for a simulated robotic arm with a two-fingered hand and nine DOFs for the ability to grasp objects with different shapes. The arm was only provided with tactile sensors. Evolved robots displayed an ability to grasp objects with different shapes, different orientations and located in varying positions within a limited area. These robots, however, were not able to deal with larger variations of the objects positions.

Buehrmann and Di Paolo (2004) evolved the control system for a simulated robotic arm with three DOFs for the ability to reach a fixed object placed on a plane and to track moving objects. The arm was provided with two pan-tilt cameras consisting of a two-dimensional array of laser range sensors placed above the robot arm and on the end-point of the robotic arm. The controller consisted of several separate neural modules. These receive different sensory information and control different motor joints. The networks are evolved separately for the ability to produce distinct elementary behaviours (e.g. change the orientation of the above camera so to focus on the object, move the first joint that determines the orientation of the arm so to orient towards the object, approaching the object by controlling the second and the third joint, etc.).

Marocco et al. (2003) use a 6 DOF arm model to evolve the ability to touch or avoid objects according to their shape. In addition to the capability of discriminating objects, the robots are also evolved for their ability to ‘name’ the object (or the action) with which they are interacting. This permitted the analysis of different social interaction protocols to investigate social and cognitive factors that support the evolutionary emergence of shared lexicons. Although this model used a very simplified arm model and limited object set and location, it provided a first attempt to use a neurorobotic model to study the link between action and linguistic representations from an evolutionary perspective.

Finally, in our previous evolutionary robotic model of reaching (Massera et al., 2006 ) we developed a realistic anthropomorphic arm with four DOFs. This is quite a different system from industrial arm robots in which each target point can be reached through an infinite number of postures and in which the relation between the joint reference system and the Cartesian reference system are much more complex and indirect. We successfully employed a method by which individuals were selected only on the basis of their ability to reach the desired target point by letting them free to develop their own strategy to solve the problem. This is in opposition to incremental approaches in which elementary components of the required final behaviour are identified by the experimenter and gradually included in the fitness evolutionary criteria.

Materials and Methods

In this section, we describe the simulated robot, the robots actuators and sensors, the architecture of the neural controller and the adaptive process used to train the robot to grasp objects of different shapes.

The robot

The robot used in the experiments reported in this paper is a simulated humanoid robot provided with anthropomorphic robotic arm with 7 actuated DOFs, a robotic hand with 20 actuated DOFs, proprioceptive and touch sensors distributed within the arm and the hand and a vision system located in the robotquotidns head.

The arm (Figure 1 A) consists mainly of three elements (the arm, the forearm and the wrist) connected through articulations displaced into the shoulder, the arm, the elbow, the forearm and wrist. The shoulder is composed of a sphere with a radius 2.8 cm. The length of arm and forearm is 23 and 18 cm, respectively. The wrist consists of an ellipsoide with a radius of 1.45, 1.2 and 1.45 cm along x-, y- and z-axis, respectively. The joints A, B and C (Figure 1 A) provide abduction∕adduction, extension∕flexion and supination∕pronation of the arm in the range [−140°, +60°], [−90°, +90°] and [−60°, +90°], respectively. These three DOFs acts like a ball-and-socket joint moving the arm in a way analogous to the human shoulder joint. The fourth DOF (D) located in the elbow is constituted by a hinge joint which provides extension∕flexion within the [−170°, +0°] range (radius–ulna bones). The fifth DOF (E) twists forearm providing pronation∕supination of the wrist–hand in the range [−90°, +90°]. The sixth and seventh DOFs (F and G) on the wrist provide flexion∕extension and abduction∕adduction of the hand within [−30°, +30°] and [−90°, +90°] ranges, respectively.

FIGURE 1

Figure 1. The kinematic chain of the arm and of the hand. Cylinders represent rotational DOFs. The axes of cylinders indicate the corresponding axis of rotation. The links amongst cylinders represents the rigid connections that make up the arm structure.

The robotic hand (Figure 1 B) is composed of a palm and 14 phalangeal segments (see Table 1 ) that make up the digits (two for the thumb and three for each of the other four fingers) connected through 15 joints with 20 DOFs. The palm consists of a box of 4.6 × 1.2 × 4.2 cm³. The thumb is composed of four connected objects: (i) an ellipsoide with a radiuns of 1.5 × 0.6 × 0.8 cm³ which is half-sunked into the palm, (ii) a box of 2.40 × 0.80 × 0.90 cm³ (corresponding to the metacarpal bones of the human thumb), (iii) a box of 1.60 × 0.75 × 0.85 cm³ (corresponding to the first phalanx) and (iv) a box of 1.12 × 0.75 × 0.80 cm³ (corresponding to the second phalanx). The other fingers are connected to the palm through knuckles represented by an ellipsoide of 0.65 × 0.65 × 0.5 cm³ of radius. The three phalanges composing a finger are boxes jointed serially.

TABLE 1

Table 1. The size (in cm) of the segments forming the hand.

The joints in the hand are grouped in the metacarpophalangeal (MP), proximal interphalangeal (PIP) and distal interphalangeal (DIP) types. Each finger has two hinge joints, PIP and DIP (see Figure 1 , right), that extend∕flex phalanges within the range [−90°, +0°]. The MP group is composed of two joints that allow both extension∕flexion and abduction∕adduction of the first phalanx of each finger. The extension∕flexion of MP is in the range [−90°, +0] for all fingers but the abduction∕adduction movement range varies for different fingers and corresponds to [−7°, +0°], [−2°, +2°], [−2°, +5°] and [+0°, +7°] for the index, the middle, the ring and the pinky fingers, respectively. The thumb does not have the DIP joint, and the MP provides three DOF located in the MP-A and MP-B joints. The former joint has two DOFs providing supination∕pronation and abduction∕adduction of metacarpal part of the thumb in [−120°, +0°] and [−15°, +90°] ranges, respectively, which allow a good opposition of the thumb with the fingers. The MP-B and PIP joints consists of hinge joints that extend∕flex the first and second phalanx of thumb in the same range of PIP and DIP joints of the other four fingers: [−90°, +0°].

The actuators

The joints of the arm are actuated by two simulated antagonist muscles implemented accordingly to the Hillquotidns muscle model (Sandercock et al., 2002 ; Shadmehr and Wise, 2005 ). More precisely, the total force exerted by a muscle (Figure 2 ) is the sum of three forces T_A(α,x) + T_P(x) + T_V(x) which depend on the activity of the corresponding motor neuron (α) and on the current elongation of the muscle (x) and which are calculated on the basis of the following equations:

where L_max and R_L are the maximum and the resting length of the muscle, T_max is the maximum force that could be generated, K_sh is the passive shape factor, b is the viscosity coefficient. The parameters of the equation are identical for all 14 muscles controlling the seven DOFs of the arm and have been set to the following values: K_sh = 3.0, R_L = 2.5, L_max = 3.7, b = 0.9, A_sh = 4.34 with the exception of parameter T_max which is set to 3000 N for joint B, to 300 N for joints A, C, D and E, and to 200 N for joints F and G.

FIGURE 2

Figure 2. An exemplification of how the force exhorted by a muscle. The graph shows how the force exhorted by a muscle varies as a function of the activity of the corresponding motor neuron and of the elongation of the muscle for a joint in which T_max is set to 300 N.

Muscle elongation is simulated on the basis of actual angular position of each DOF, which is mapped linearly within the allowable angular range of each DOF. For instance, in the case of elbow where the limits are [−170°, +0°], this range is mapped onto [+1.3, +3.7] for the agonist muscle and inversely [+3.7, +1.3] for antagonist muscle. Hence, when elbow is completely extended (angle 0), the agonist muscle is completely elongated (3.7) and antagonist completely compressed (1.3), and vice versa when elbow is flexed.

In the case of the hand, the positions of the joints are controlled by a limited number of variables (i.e. they are interdependent as in the case of human hands) through a velocity-proportional controller (joint maximum velocity is set to 0.30 rad∕second). More precisely, the force exhorted by the MP, PIP and DIP joints (MP-A, MP-B and PIP in the case of the thumb) which determine the extension∕flexion of the corresponding finger are controlled by a single variable theta ranging between [−90°, +0°]. The desired position of the three joints is set to theta, theta and (2.0∕3.0)*theta, respectively. In the case of the thumb, the supination∕pronation is also controlled by theta by setting the desired angle to −(2.0∕3.0)theta. The DOF which determine the abduction∕adduction of the first phalanx of each finger is controlled by a second variable which has been set to the constant value of 0.0 rad.

The total weight of the arm and of the hand is 520.47 g. The robot and the robot∕environmental interactions have been simulated by using Newton Game Dynamics (NGD, see: http://www.newtongamedynamics.com/ ), a library for accurately simulating rigid body dynamics and collisions.

The sensors

The robot is provided with proprioceptive sensors which encode the current position of the DOFs of the arm and the hand, tactile sensors distributed over the hand, and of the vision system located on the robot head.

Seven arm propriosensors encode the current angles of the seven corresponding DOFs located on the arm and on the wrist normalized in the range [−1, +1]. Five hand propriosensors encode the current extension∕flexion state of the five corresponding fingers in the range [0, 1] where 0 means fully extended and 1 means fully flexed. The hand propriosensors report the actual value of the MP-B joint for the thumb and the PIP joints of fingers. Due to compliance of fingerquotidns joints when the hand hit with an object and to the fact that the state of the three corresponding DOFs is summarized in a single variable, the same sensory state might correspond to a different states of the MP and DIP joints.

The six tactile sensors measure whether the five fingers and the part constituted by the palm and wrist are in physical contact with another object. More precisely, each sensor encodes the number of contacts occurring in the corresponding body part normalized in the range [0, 1] through a logistic function with 0.2 as slope coefficient. The three vision sensors encode the output of a vision system (which has not been simulated) that computes the relative distance of the object with respect to the hand up to a distance of 80 cm normalized in the range [−1, +1] over three orthogonal axes.

The reason behind the choice of this particular sensory system configuration is that to study situations in which the vision and tactile sensory channels need to be integrated. In isolation, each of the two types of sensor does not provide enough information to perform the task.

The neural controller

The robot is provided with the neural controllers shown in Figure 3 which include 21 sensory neurons, five internal neurons with recurrent connections and 16 motor neurons.

FIGURE 3

Figure 3. The architecture of the neural controllers. Arrows indicated blocks of fully connected neurons. Internal and hand actuators neurons are also provided with a bias.

The object position sensors, arm and hand propriosensors and tactile sensors encode the state of the corresponding sensors described above. The actuators of the arm encode the activity of the 14 motor neurons controlling the corresponding muscles of the arm. The two actuators of the hand encode the desired extension∕flexion state of the thumb and of the other four fingers, respectively (i.e. the four fingers are not controlled independently).

The state of the sensors, the desired state of the actuators and the internal neurons are updated every 0.010 second. The activity of the internal and motor neurons is calculated on the basis of a standard logistic function (with a slope coefficient of 0.5 in the case of the internal neurons and of 1.0 in the case of the motor neurons). In the case of the arm actuators and of the internal neurons, the output of the neuron corresponds to the neuronsquotidn activity. In the case of the hand actuators and the tactile sensors, instead, the output of the neurons is also depends from the neurons previous activation. More precisely, these neurons consist of leaky integrators in which the output is calculated on the basis of the following equation (Nolfi and Marocco, 2001 ):

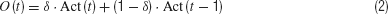
where Act is the activity of the neuron calculated on the basis of the logistic function (with slope coefficient 0.2 for tactile sensors and 1.0 for hand actuators) and δ is a time constant parameter ranging between [0, +1] (for alternative ways to implement leaky neurons see, for example, Beer, 1995 ).

The main criteria behind the choice of this particular neural network architecture have been to reduce the number of assumptions to the minimum and to reduce the number of free parameter as much as possible. A systematic analysis of the role of the architecture will be made in future work. For the moment, the analysis of the results obtained by varying some of the aspects of the architecture (results not shown) did not lead to qualitatively different results.

The adaptive process

The free parameters of the neural controller, i.e. the connection weights, the biases of internal neurons and hand actuators and the time constant of leaky-integrator neurons, have been adapted through an evolutionary robotics method (Nolfi and Floreano, 2000a ).

The initial population consisted of 100 randomly generated genotypes, which encode the free parameters of 100 corresponding neural controllers. Each parameter is encoded with 16 bits. Each genotype contains 6096 bits corresponding to 381 free parameters: 366 connection weights and 7 biases normalized in the range [−10, +10] and 8 time constant normalized in the range [0.0, 1.0]. The 20 best genotypes of each generation were allowed to reproduce by generating five copies each. Four out of the five copies are subjected to mutations and one copy is left intact. During mutation each bit of the genotype has a 1.5% probability to be replaced with a new randomly selected value. The evolutionary process is continued for 400 generations (i.e. the process of testing, selecting and reproducing robots is iterated 400 times). The experiment was replicated 10 times.

The robot is adapted for the ability to grasp spherical and cylindrical objects placed on a table located in front of the robot. The objects can move freely by eventually falling off the table (Figure 1 A). During the adaptive process, each genotype is translated into a corresponding neural controller, embodied in the simulated robot and tested for 18 trials. Each trial lasts 4 second corresponding to 400 steps. At the beginning of each trial the arm is set in the ith of the 18 corresponding predefined postures shown in Figure 4 . The target object is placed in a fixed position in the central portion of the table. Spherical objects have a radius of 2.5 cm and a weight of 32.72 g, cylindrical objects have a radius of 2.0 cm, a height of 6.0 cm and a weight of 37.70 g.

FIGURE 4

Figure 4. The 18 initial postures of the arm and of the hand used during the 18 corresponding trials.

Evolving robots are evaluated on the basis of the following two componentsquotidn fitness function which reward reaching and grasping behaviours, respectively

where dist encodes the distance between the barycentre of the hand and the object, grasp encode whether an object has been successfully grasped (i.e. grasp is 1 when the target object is elevated with respect to the table and is in physical contact with the robot hand and is 0 otherwise), t is the current trial and s is the current time step. To allow the robot to reach and grasp the object, the fitness is calculated only in the second-half of each trial (i.e. from time step 200 to time step 400). The constant at the beginning of the function, which corresponds to the maximum fitness that can be gathered by grasping each object during the first phase of each trial and by holding the object above the plane for the rest of the trial, is used to normalize the fitness value in the range [0, 1].

Results

By analysing the behaviour of the evolved robots throughout generations, we observed that in 8 out of 10 replications of the experiment evolving robots develop an ability to reach and grasp objects which allows them to display optimal or close to optimal performance (see Figure 5 ).

FIGURE 5

Figure 5. The fitness of the best individual throughout generations for 10 replications of the experiment.

By analysing the behaviour of the best evolved individual of one of the most successful replication, we observed that it successfully grasp the two types of objects from any of the 18 initial postures described above. As shown in Figure 6 , the behaviour displayed by this individual can be divided into three phases: (1) an initial phase in which the arm moves towards the object by first increasing and then decreasing the movement speed and in which the hand initiates to flex, (2) a second phase in which the tactile sensors start to be activated, the arm stays still or almost still and in which the wrist and the fingers flex around the object, (3) a final phase in which the arm rotates and moves the wrist so to lift the object from the table and so to reduce the risk that the object fall down from the hand. A set of video showing the behaviour of evolved robots in detail can be accessed from the following Web page: http://laral.istc.cnr.it/esm/arm-grasping/ http:∕∕laral.istc.cnr.it∕esm∕arm-grasping∕.

FIGURE 6

Figure 6. Five superimposed snapshots of the behaviour displayed by one of the best evolved robots. (A) The evolved robot grasping a sphere; (B) The same evolved robot grasping a cylinder.

By testing evolved robots in different conditions with respect to the condition in which they have been evolved, we observed that they display remarkable generalization abilities with respect to the position of the object on the table and with respect to the shape of the object.

Figure 7 shows the average performance of the best evolved robots of three of the best replications of the experiment observed by systematically varying the position of the objects on the table. As can be seen, although different individuals vary with respect to their generalization capabilities, they all display rather good performance on the central diagonal area which corresponds to the preferential trajectory followed by the arm in normal conditions (i.e. when the objects are placed on the central position of the table). The decrease in performance on the top-right and bottom-left part of the table can be explained by considering that grasping objects located in these positions require postures which differ significantly from those assumed by the robots to grasp objects in the central area of the table.

FIGURE 7

Figure 7. Performance of the best evolved robots of the three best replications of the experiment.

Each robot has been tested in 120 different conditions corresponding to 60 different position of the object on the table and to two types of objects (spherical and cylindrical objects). For each testing condition, the robot has been tested for 18 trials corresponding to the 18 different starting position of the arm. The colours of the rectangles indicate the performance. For each picture, the left and right areas correspond to the left and right area of the table with respect to the robot, respectively. The top and bottom areas correspond to the proximal and distant areas of the table with respect to the robot, respectively.

By testing evolved robots in environment containing the objects shown in Figure 8 , we also observed that evolved robots display remarkable generalization abilities with respect to the shape and size of the objects (see Figure 9 ).

FIGURE 8

Figure 8. Objects used for testing robotsquotidn generalization ability with respect to object shape and size.

FIGURE 9

Figure 9. Performances of the evolved robots of the seven best replications of the experiment observed by testing the robots with the eight objects shown in Figure 8 .

The difference in performance amongst the individual robots of different replications of the experiment are due to the different behavioural strategies displayed by evolved individuals with particular reference to the second and third phases of the behaviour in which the robots grasp and lift the objects (for more information, see the video available from http://laral.istc.cnr.it/esm/arm-grasping/ http:∕∕laral.istc.cnr.it∕esm∕arm-grasping∕). For example, the fact that best individual of replication 1 displays poor performance with objects 2, 4, 6 and 7 with respect to other evolved individuals is due to the fact that it flexes its fingers very quickly. This type of strategy, in fact, prevents this robot from the possibility of exploiting the adjustments of the relative position of the fingers with respect to the objects which arise spontaneously in time as a result of the effects of the forces exhorted by the hand, the collisions between the fingers and the object and the compliance of the hand The poor performance of the best individuals of replication 7 on objects 2, 3 and 4 can be explained by considering that the way in which this individual lifts the objects after the grasping phase tends to produce collisions with the plane in the case of big objects which might cause the falling down of the object from the hand. Finally, the good performance of replication 8 can be explained by the ability of this robot in controlling the thumb, which is crucial for grasping difficult slippery objects, and by the fact that this robot produces a limited rotation of the arm and of the wrist during the lifting phase which minimize the risk of collisions with the plane after the objects have been grasped.

Overall these results suggest that certain behavioural strategies might be effective for a large variety of objects and that the limited differences in terms of shape and size of the objects to be grasped should not necessarily have an impact on the rules that regulate the robot∕environmental interactions.

Although a systematic analysis which can allow us to identify the factors that lead to such good generalization ability will be carried out in future work, preliminary analysis (not shown) suggest that the muscle-like properties of the actuators of the arm and the compliance of the actuators of the fingers combined with the adaptation process, which manages to exploit these properties, play an important role. With respect to the compliance of the fingers, in particular, it greatly simplifies the problem of adapting the postures of the fingers to the shape of the object. Regarding the generalization ability with respect to the position of the object, an important factor is constituted by the fact that the position of the object extracted by the vision system is encoded in relation to the position of the hand.

Discussion

In this paper, we showed how effective reaching and grasping behaviour can be developed through a trial and error process in which the free parameters encode the control rules which regulate the fine-grained interaction between the robot and the environment and variation of the free parameters are retained or discarded on the basis of their effects at the level of the global behaviour exhibited by an anthropomorphic robotic arm situated in the environment and provided with muscle-like actuators. The robots are let free to choose the way in which the problem can be solved during the adaptation process, since they are rewarded only with respect to their ability to approach and lift objects irrespectively of the particular trajectory with which they approach the objects, the posture of the arm and of the hand that they assume, and the way in which different motor actions produced by the robot in interaction with the environment are distributed over time.

The experimental setup presented in the paper is significantly more advanced with respect to previous works based on similar adaptive techniques (Bianco and Nolfi, 2004 ; Buehrmann and Di Paolo, 2004 ; Gomez et al., 2005 ; Massera et al., 2006 ) with respect to the morphology of the robot (which an anthropomorphic robotic arm and hand with 27 DOFs), with respect to the size of the neural controller and to the dimensionality of the corresponding search space and with respect to the task which involved the ability to reach and grasp freely moving objects with different shapes placed on a table which constraints the movements of the robot.

The obtained results demonstrate how the proposed methodology and the exploitation of the properties which arise from the physical interaction between the robot and the environment allow the robot to produce effective behaviours on the basis of a parsimonious control system. For example, the effects of the collisions between the fingers of the robotic hand and the objects being grasped combined with the compliance of the fingerquotidns joints allow the spontaneous conformation of the robot hand to the shape of the object which in turn allows the robot to effectively grasp objects with different shapes and orientations without the need of control mechanisms able to regulate the movement of the arm and of the hand on the basis of the characteristics of the objects.

This line of research is also consistent with recent cognitive robotics approaches such as in the field of developmental robotics (Lungarella and Metta, 2003 ). Developmental robotics, also known as epigenetic robotics, in an interdisciplinary approach to robot design. Developmental robots are characterized by a prolonged developmental process through which varied and complex cognitive and perceptual structures emerge as a result of the interaction of an embodied system with a physical and social environment. Lungarella and Metta show that although most of the current developmental robotic investigations have focussed on sensorimotor control (e.g. reaching) and social interaction (e.g. gaze control), future cognitive robotics research should go beyond gazing, pointing and reaching. In order to design truly autonomous behaviour, future robotics research should integrated motor control with better sensory and motor apparata, more refined value-based learning mechanisms and means of exploiting neural and body dynamics.

This neurorobotic approach also has a potential relevance to computational neuroscience research on motor control (Shadmehr and Wise, 2005 ). The current architecture of the robotquotidns neural controller has not been constrained on any specific brain region known to be involved in limb control. Therefore, the current model and simulation results cannot be used to make any speculation on the relevance to neuroscience research. However, future extensions of the model might focus specifically on investigating the role and structure of the neural network controller and its mapping onto brain regions and circuitries (e.g. cerebellum, motor areas) known to be involved in prehension ability (Jones and Lederman, 2006 ; Kawato, 2002 ). This would also make possible the testing of current theories of minimization criteria such as energy minimum, jerk minimum and stability maximization, for generating voluntary movements and the comparison between robotic model results and limb neurophysiology literature (Shadmehr, 2002 ). For example, recent evolutionary robotic models on the development and integration of action and language capabilities have demonstrated that neural network architectures can be constrained to reflect known neurophysiological phenomena (Arbib et al., 2000 ; Cangelosi and Parisi, 2004 ). For example, Cangelosi and Parisi (2004) used synthetic brain imaging techniques to demonstrate that the region of the robotquotidns neural network that specializes for sensorimotor integration is also involved in the processing of the names of actions (verbs), whilst the network region specialized in the representation and categorization of visual information only is also involved in the processing of the names of objects (nouns).

In future work, we plan to extend the variability of the objects to be grasped in order to investigate problems which require an ability to display a variety of qualitatively different approaching and grasping strategies. Within this future research line, we would like to study how neurocontrollers, developed through the methodology described in this paper, can be complemented with additional mechanisms which, on one hand might favour the development of different behavioural strategies and, on the other hand might allow the robot to select the approaching and grasping strategy which is appropriate to the current robot∕environmental circumstances. To achieve this goal, we plan to implement and to compare different mechanisms such as continuous time recurrent neural networks including neurons varying at tuneable time scales (Beer, 2005 ; Nolfi and Marocco, 2001 ) and internal models operating at the level of elementary behaviour rather than at the level of the fine-grained robot∕environmental interactions (i.e. which allow the robot to select the behavioural strategy which produces a desired effect by exploiting the ability of forecasting the global effects of the execution of a given behavioural strategy in a given robot∕environmental situation, see (Tani et al., 2004 ) and Nishimoto et al., in press).

Moreover, to address the relevance of such a simulation model to research with physical robotic platform, we are currently involved in a collaborative project to test the evolved controllers on the RobotCub physical robot (Sandini et al., 2004 http://www.robotcub.org ). This will allow us to verify the accuracy of the simulator and to revise the experiments performed in simulation so to progressively reduce the gap between the simulated and the real robot∕environmental systems.

Supplemental Data

Supplemental data for this article including movies of the behaviours displayed by evolved robots of different replications of the experiment can be found at the following address: http://laral.istc.cnr.it/esm/arm-grasping .

Conflict of Interest Statement

We declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgements

The research has been supported by the ECAGENTS project funded by the Future and Emerging Technologies programme (IST-FET) of the European Community under EU R&D contract IST-1940.

References

Arbib, M. A., Billard, A., Iacoboni, M., and Oztop, E. (2000). Synthetic brain imaging: grasping, mirror neurons and imitation. Neural Netw. 13, 975–997.

Pubmed Abstract | Pubmed Full Text

Beer, R. D. (1995). On the dynamics of small continuous-time recurrent neural networks. Adapt. Behav. 3, 471–511.

Beer, R. D. (2005). A dynamical systems perspective on agent-environment interaction. Artif. Intell. 72, 173–215.

Bianco, R., and Nolfi, S. (2004). Evolving the neural controller for a robotic arm able to grasp objects on the basis of tactile sensors. Adapt. Behav. 12(1), 37–45.

Buehrmann, T., and Di Paolo, E. A. (2004). Closing the loop: Evolving a model-free visually-guided robot arm. In Proceedings of the Ninth International Conference on the Simulation and Synthesis of Living Systems (ALIFE9) (Boston, Cambridge, MA, MIT Press).

Cangelosi, A., Bugmann, G., and Borisyuk, R. (2005). Modeling Language, Cognition and Action: Proceedings of the 9th Neural Computation and Psychology Workshop (Singapore, World Scientific).

Cangelosi, A., and Parisi, D. (2004). The processing of verbs and nouns in neural networks: insights from synthetic brain imaging. Brain Lang. 89, 401–408.

Pubmed Abstract | Pubmed Full Text

Corballis, M. C. (2003). From hand to mouth: the origins of language.

Gallese, V., and Lakoff, G. (2005). The brainquotidns concepts: the role of the sensory-motor system in conceptual knowledge. Cogn. Neuropsychol. 21.

Gomez, G., Hernandez, A., Eggenberger Hotz, P., and Pfeifer, R. (2005). An adaptive learning mechanism for teaching a robotic hand to grasp. In International Symposium on Adaptive Motion of Animals and Machines.

Jones, L. A., and Lederman, S. J. (2006). Human hand function.

Kawato, M. (2002). Cerebellum and motor control. In Handbook of Brain Theory and Neural Networks, 2nd edn, M. A. Arbib, ed. (Cambridge, MA, MIT Press), pp. 190–195.

Krose, B. J. A., and Van der smagt, P. P. (1993). An introduction to neural networks.

Lungarella, M., and Metta, G. (2003). Beyond gazing, pointing reaching: A survey of developmental robotics. Paper presented at: 3rd International Workshop on Epigenetic Robotics (Boston, USA).

Marocco, D., Cangelosi, A., and Nolfi, S. (2003). Evolutionary robotics experiments on the evolution of language. Philos. Trans. R. Soc. Lond. A 361, 2397–2421.

Pubmed Abstract | Pubmed Full Text

Massera, G., Cangelosi, A., and Nolfi, S. (2006). Developing a reaching behaviour in a simulated anthromorphic robotic arm through an evolutionary technique. In Artificial Life X: Proceeding of the Tenth International Conference on the simulation and synthesis of living systems (Cambridge, MA, MIT Press).

Mial, R. C. (2002). Motor control, biological and theoretical. In Handbook of Brain Theory and Neural Networks, 2nd edn (Cambridge, MA, MIT Press), pp.110–113.

Nolfi, S., and Floreano, D. (2000a). Evolutionary robotics: the biology, intelligence technology of self-organizing machines (Cambridge, MA, MIT Press/Bradford Books).

Nolfi, S., and Floreano, D. (2000b). Evolutionary robotics: the biology, intelligence technology of self-organizing machines.

Nolfi, S., and Marocco, D. (2001). Evolving robots able to integrate sensory-motor information over time. Theory Biosci. 120, 287–310.

Pulvermuller, F. (2005). Brain mechanisms linking language and action. Nat. Rev. Neurosci. 6, 576–582.

Pubmed Abstract | Pubmed Full Text

Rizzolatti, G., and Arbib, M. A. (1998). Language within our grasp. Trends Neurosci.

Pubmed Abstract | Pubmed Full Text

Sandercock, T. G., Lin, D. C., and Rymer, W. Z. (2002). Muscle models. In Handbook of Brain Theory and Neural Networks, 2nd edn, M. A. Arbib, ed. (Cambridge, MA, MIT Press), pp. 711–715.

Sandini, G., Metta, G., and Vernon, D. (2004). RobotCub: an open framework for research in embodied cognition. Paper presented at: Fourth International Conference on Humanoid Robots.

Schaal, S. (2002). Arm and hand movement control. In Handbook of Brain Theory and Neural Networks, 2nd edn, M. A. Arbib, ed. (Cambridge, MA, MIT Press), pp. 110–113.

Shadmehr, R. (2002). Equilibrium point hypothesis. InHandbook of Brain Theory and Neural Networks, 2nd edn (Cambridge, MA, MIT Press), pp. 409–412.

Shadmehr, R., and Wise, S. P. (2005). The computational neurobiology of reaching and pointing (Cambridge, MA, MIT Press).

Tani, J., Ito, M., and Sugita, Y. (2004). Self-organization of distributedly represented multiple behavior schemata in a mirror system: reviews of robot experiments using RNNPB. Neural Netw. 17, 1273–1289.

Pubmed Abstract | Pubmed Full Text

Torras, C. (2002). Robot arm control. In Handbook of Brain Theory and Neural Networks, 2nd edn (Cambridge, MA, MIT Press), pp. 979–983.

Wolpert, D. M., and Flanagan, J. R. (2002). Sensorimotor learning. In Handbook of Brain Theory and Neural Networks, 2nd edn, M. A. Arbib, ed. (Cambridge, MA, MIT Press), pp. 1020–1023.