Teorema de Thales
- 1. Teorema de Thales Esta presentación fue pensada y creada como un apoyo para los alumnos que necesitan aclarar ideas relacionadas con este teorema
- 2. Teorema de Thales Nació : alrededor del año 640 AC en Mileto, Asia Menor (ahora Turquía) Thales era considerado uno de los siete sabios de Grecia Algunos datos Thales era un hombre que se destacó en varia áreas : comerciante, hábil en ingeniería, astrónomo, geómetra
- 3. una noche Thales estaba observando el cielo y tropezó. Un sirviente lo Levantó y Le dijo: cómo pretendes entender lo que pasa en el cielo, si no puedes ver lo que está a tus pies. Una anécdota contada por Platón Sobresale especialmente por: Que en sus teoremas geométricos aparecen los inicios del concepto de demostración y se podría decir que son el punto de partida en el proceso de organización racional de las matemáticas.
- 4. Se cuenta que comparando la sombra de un bastón y la sombra de las pirámides, Thales midió, por semejanza, sus alturas respectivas. La proporcionalidad entre los segmentos que las rectas paralelas determinan en otras rectas dio lugar a lo que hoy se conoce como el teorema de Thales.
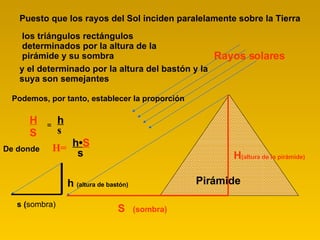
- 5. Pirámide Puesto que los rayos del Sol inciden paralelamente sobre la Tierra los triángulos rectángulos determinados por la altura de la pirámide y su sombra Podemos, por tanto, establecer la proporción H S = h s De donde H= h • S s y el determinado por la altura del bastón y la suya son semejantes Rayos solares S (sombra) H (altura de la pirámide) s ( sombra) h (altura de bastón)
- 6. Ahora El famoso teorema
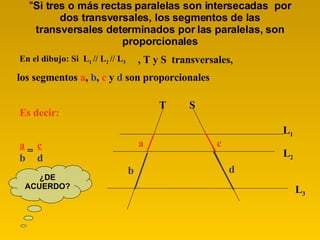
- 7. " Si tres o más rectas paralelas son intersecadas por dos transversales, los segmentos de las transversales determinados por las paralelas, son proporcionales En el dibujo: Si L 1 // L 2 // L 3 , T y S transversales, los segmentos a , b , c y d son proporcionales Es decir: = ¿DE ACUERDO? T S L 1 L 2 L 3 a a b b c c d d
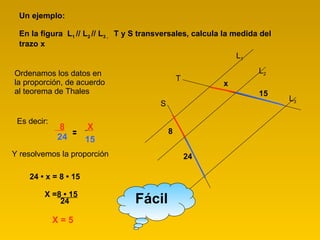
- 8. Un ejemplo: En la figura L 1 // L 2 // L 3 , T y S transversales, calcula la medida del trazo x Ordenamos los datos en la proporción, de acuerdo al teorema de Thales Es decir: = Y resolvemos la proporción 24 • x = 8 • 15 X = 8 • 15 24 X = 5 Fácil L 1 L 2 L 3 T S 8 24 x 15 8 24 X 15
- 9. Otro ejemplo: en la figura L 1 // L 2 // L 3 , T y S son transversales, calcula x y el trazo CD Formamos la proporción = Resolvemos la proporción 3(x + 1) = 2(x + 4) 3x + 3 = 2x + 8 3x - 2x= 8 - 3 X=5 Luego, como CD = x + 4 CD= 5 + 4 = 9 3 2 x+4 x+1 L 1 L 2 L 3 T S x+4 x+1 3 2 C D
- 10. Y nuevamente pensando en la pirámide….. TRIÁNGULOS DE THALES Dos triángulos se dicen de Thales o que están en posición de Thales, cuando: Tienen un ángulo común y los lados opuestos a dicho ángulo son paralelos . Podemos ver esto si trasladamos el triángulo formado por el bastón, su sombra y los rayos solares hacia el formado por la pirámide S (sombra) H (altura de la pirámide) s ( sombra) h (altura de bastón)
- 11. Triángulos de Thales En dos triángulos de Thales, sus lados, tienen la misma razón de semejanza De acuerdo a esto, en la figura BC// ED, entonces, con los lados de los triángulos AED y ABC ocurre: = O también = A esta forma de tomar los trazos, se le llama “la doble L” B C A D E AE AB ED AE ED AB BC BC
- 12. Aplicaciones de esta idea Calcula la altura del siguiente edificio Escribimos la proporción = Y resolvemos la proporción 3 • x = 5 • 15 x = 75 3 X = 25 Por que 3+12=15 x 5 3 12 3 5 15 x
- 13. Otro ejercicio En el triángulo ABC, DE//BC , calcule x y el trazo AE Formamos la proporción = Resolvemos la proporción Por que x+3+x = 2x+3 8(2x + 3) = 12( x + 3) 16x + 24 = 12x + 36 16x – 12x = 36 – 24 4x = 12 X = 12 = 3 4 Por lo tanto, si AE = x + 3 = 3 + 3 = 6 A B C x+3 x 8 12 D E 8 X+3 12 2x+3