Riesgo 1C2010

Risk Management

Finanzas II
Universidad Católica Argentina
Abril 2010

Lic. Alejandro Salevsky
Lic. Pablo Ylarri
Lic. Juan Manuel Cascone
Lic. Clara Llerena
Lic. Santiago de Lavallaz

Índice

01 Noticias

02 Conceptos Generales

03 Medición del riesgo en activos y portfolios.

04 Markowitz. Teoría de portfolios eficientes

05 Sensibilidad y Escenarios

http://condensadordeflujo.wordpress.com

Anoticiándonos


Qué entendemos por riesgo
02 Y cómo lo identificamos en la crisis subprime …


Y cómo lo identificamos en nuestro país…


Riesgo

•Está dado por la variabilidad de los retornos de un activo determinado
•Es la posibilidad que los flujos de fondos reales sean diferentes a los
Concepto flujos de fondos pronosticados

•Si el retorno es conocido con certeza, es una inversión libre de riesgo

•La diferencia entre el retorno de un activo riesgoso y el retorno de un
activo libre de riesgo es la prima de riesgo.
Prima de
riesgo •Los datos históricos sobre retornos de los activos son una de las posibles
fuentes de información sobre primas de riesgo y desviaciones
estándar.

•El riesgo de un activo no puede ser evaluado aisladamente. A veces al
agregar un activo riesgoso a un portfolio se reduce el riesgo total
Hedging del portfolio.
•Se denomina hedging a la acción de invertir en un activo riesgoso con el
objetivo de reducir el riesgo total del portfolio.
•¿Qué retorno nos asegura una inversión libre de riesgo?
?

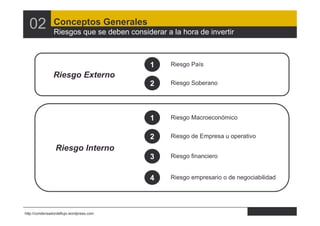
Análisis de riesgos


Riesgos que se deben considerar a la hora de invertir

1 Riesgo País
Riesgo Externo
2 Riesgo Soberano

1 Riesgo Macroeconómico

2 Riesgo de Empresa u operativo

Riesgo Interno
3 Riesgo financiero

4 Riesgo empresario o de negociabilidad


From 1992, Leeson made unauthorized speculative trades that at first
made large profits for Barings; £10 million which accounted for 10% of
Barings' annual income. He earned a bonus of £130,000 on his salary of
£50,000 for that year.
However, his luck soon went sour, and he used one of Barings' error
accounts (accounts used to correct mistakes made in trading) to hide his
losses. The account was numbered 88888 -- a number considered very
lucky in Chinese numerology. Leeson claims that this account was first
used to hide an error made by one of his colleagues; rather than buy 20
contracts as the customer had ordered, she had sold them, costing
Barings £20,000.
However, Leeson used this account to cover further bad trades. He insists
that he never used the account for his own gain, but in 1996 the New
York Times quoted "British press reports" as claiming that investigators
had located approximately $35 million in various bank accounts tied to
him.
By the end of 1992, the account's losses exceeded £2 million, which
ballooned to £208 million by the end of 1994


Sus superiores descubrieron que los descalabros financieros se
relacionaban con su persona el 19 de enero de 2008 y esto coincidió con
la "Crisis bursátil de enero 2008". Según Daniel Bouton, presidente del
banco, el fraude Kerviel es en realidad bastante sofisticado. En práctica,
Kerviel apostó una suma extraordinaria a que ciertas acciones subirían o
bajarían y "perdió la apuesta". Cuando el banco se dio cuenta de las
operaciones e intentó deshacerlas, ya estaba en medio de la crisis
financiera que afectaba la globalidad de los mercados internacionales y
perdió 4900 millones de euros. Según explicó Burton, Kerviel utilizó un
complejo sistema para ocultar sus operaciones bajo falsas transacciones
y gracias a su conocimiento del sistema del banco el cual lo consideraba
uno de sus mejores empleados.


New!

Fabrice Tourre

Acá
toy!


Algunos Ejemplos
02
De cómo su mala gestión puede llevar a la quiebra

• Inglaterra, febrero de 1995: el banco inglés Baring quiebra como resultado de
tremendas pérdidas en sus posiciones de futuro del índice de acciones japonesas. El
ejecutivo Nick Leeson había comprado ocho mil millones de dólares en futuros,
apostando al alza del índice Nikkei de la bolsa de Tokio. Pero el índice se desplomó, en
parte por el terremoto de Kobe. En sólo un mes, Baring perdió 1.200 millones de
dólares y terminó en la quiebra.

• Septiembre de 1995: un incidente similar ocurrió en la sucursal neoyorkina del banco
japonés Daiwa. El responsable fue Toshihide Iguchi quien perdió 1.100 millones de
dólares especulando con bonos. Si bien el banco Daiwa (décimo de Japón) no quebró,
perdió los beneficios de todo un año.

•¿Qué tipos de riesgos podemos identificar en ambos eventos?
?

Fuente: Materia Biz


Riesgo y retorno de un activo y un portfolio
Existen dos actividades a la hora de invertir

1 2

Research sobre el activo
y el mercado con el
objetivo de determinar Formación de un portfolio
el riesgo y el retorno óptimo de activos
de cada activo en
particular.


Riesgo: key Issues

1. Portfolio combinado de activos con y sin riesgo
2. Frontera eficiente
3. Capital Asset Pricing Model
4. Capital Market Line
5. Security Market Line
6. Análisis de sensibilidad y escenarios


03 Medidas de riesgo
Probabilidad de ocurrencia. Análisis histórico

•Una inversión es riesgosa pues el emisor puede no pagar intereses o capital del
bono o puede no cumplirse los pagos esperados en cualquier otro tipo
de activo.
Probabilidad
de ocurrencia
•Los posibles retornos son variables y puede asignarse una probabilidad
a cada resultado

•La probabilidad de ocurrencia es la probabilidad de que un determinado
resultado se produzca.
• El rendimiento esperado de una inversión
se obtiene a través de la
sumatoria
del producto entre el retorno de
cada escenario y su
probabilidad de ocurrencia.

n

r = ∑r i
pi
i =1


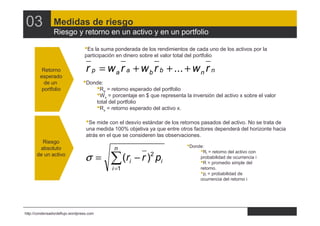
Riesgo y retorno en un activo y en un portfolio

•Es la suma ponderada de los rendimientos de cada uno de los activos por la
participación en dinero sobre el valor total del portfolio

Retorno r p = w a r a + w b r b + ... + w n r n
esperado
de un •Donde:
portfolio •Rp = retorno esperado del portfolio
•Wx = porcentaje en $ que representa la inversión del activo x sobre el valor
total del portfolio
•Rx = retorno esperado del activo x.
•Se mide con el desvío estándar de los retornos pasados del activo. No se trata de
una medida 100% objetiva ya que entre otros factores dependerá del horizonte hacia
atrás en el que se consideren las observaciones.
Riesgo
absoluto n •Donde:
•Ri = retorno del activo con
de un activo
σ= ∑ (ri − r )2 pi probabilidad de ocurrencia i
•R = promedio simple del
i =1 retorno.
•pi = probabilidad de
ocurrencia del retorno i


Riesgo y retorno en un activo y en un portfolio

•Es la relación entre el riesgo (desvío estándar) y el retorno (retorno promedio). Se
denomina genéricamente coeficiente de variación.

σ
Riesgo
relativo
CV =
•Donde:
de un activo •σ=desvío estándar
•R= retorno promedio
r
•A diferencia del retorno, para la determinación del riesgo de un portfolio jamás se
deben promediar los riesgos de los activos debido a la presencia de
correlaciones entre ellos.

Riesgo σ p = w a σ a + w bσ b + 2w aw bCOVa,b
2 2 2 2
absoluto
de un
portfolio COVa,b = σ aσ b ρ a,b
de 2 activos
•Donde:
•Wx = porcentaje en $ que representa la inversión del activo x sobre el valor
total del portfolio
•σx = desvío estándar del activo x
•COVa,b=covarianza entre el activo A y el activo B
•Ρa,b=coeficiente de correlación entre el activo A y el activo B


Caso: Riesgo y Retorno de un Portafolio
03
• Dados los siguientes datos

Concepto Empresa A Empresa B

Rendimiento 12% 18%

Desvío estándar 20% 40%

Composición del portafolio 30% 70%

Calcule:
a) Retorno esperado del portafolio
b) Desvío estándar del portafolio, si el coeficiente de correlación entre
los activos es 0,42.

? ¿Si dos flujos de fondos tienen el mismo riesgo absoluto, tendrán
también el mismo riesgo relativo?


Ejemplo

PROYECTO “A” PROYECTO “B”

Rendimiento
esperado $ 2000 $ 2450

Desvío
estándar $ 774,60 $ 1.781,15

Coeficiente
de variación 0,39 0,73

Intervalo
de confianza $450.80 / $3549,20 -$1.112,30 / $6012,30

? ¿Ud. cuál elige?


04 Markowitz. Teoría de porfolios eficientes
Determinación de la cartera óptima

Frontera Eficiente
r
I2 •La cartera óptima del inversionista estará dada por
I1 el punto de tangencia entre la curva de indiferencia
del inversor y la frontera eficiente.
C
•La curva de indiferencia del inversor responde a
A su propensión al riesgo.
Conjunto
de
•Elección de una cartera por parte del inversionista –
Portfolios
B invertir todo su dinero en ella.

•Aún no hay mecanismos que le permitan endeudarse
o prestar dinero – sólo activos riesgosos.

σ

•¿Por qué el inversor no elige un punto distinto al de tangencia sobre
? la frontera eficiente ?


Capital Market Line (CML) - Generalidades

a. Portfolio A compuesto por wxX, wyY, wzZ. Retorno A
@ riesgo A
r
b. Portfolio B compuesto por wmM, wnN, wqQ. Retorno B
CML
da + @ riesgo B
Deu Asset
ky
Ris c. Porfolio C. Máximo retorno a riesgo C
G
+
nds
Rf Bo Asset d. Portfolio D. Máximo retorno a riesgo D.
ky D
Ris
H e. Portfolio E. Retorno E @ riesgo E. Ineficiente ya que
Conjunto B
C tiene mismo riesgo y más retorno.
C de
F
A
Portfolios f. Portfolio F = porfolio de mercado + inversión en activo
libre de riesgo.
g. Portfolio G = portfolio de mercado + endeudamiento a
E tasa libre de riesgo

σ h. Portfolio H: portfolio puro de mercado

•¿Cuál es la mejor inversión?
? •¿Es posible en la realidad pasar de F a G?
•¿Qué efecto tiene en el mercado una suba de tasas?


Capital Market Line (CML) – Caso I

r
CML
da +
Deu Asset a) ¿Cuál será el retorno esperado y el desvío
ky
Ris
G de un portfolio formado por un 110% de
+
nds colocación en un activo riesgoso, cuya
Rf Bo Asset
ky D
Ris esperanza de retorno es del 16% y un desvio
H
B
estándar del 30%?
Conjunto
C de La tasa libre de riesgo activa es del 8% y la
F
A
Portfolios pasiva del 5%.
b) ¿En qué proporciones debe armarse el
portfolio para que tenga una esperanza de
E retorno del 9%?
σ


Capital Market Line (CML) – Takeaways

r
CML •Los inversores obtienen portfolios eficientes al
da + combinar activos libres de riesgo con
Deu Asset
ky
Ris activos riesgosos
G
+
nds
Rf Bo Asset
Ris
ky D •Todos los portfolios ideales están sobre la
H CML y tienen una base de rendimiento mínimo
Conjunto B
igual a rf.
C de
F
A
Portfolios •Es necesario separar la decisión de inversión de
la de financiamiento. La aversión al riesgo
determina el monto de deuda a tomar/prestar
E •La pendiente de la CML es el trade-off riesgo-
retorno y es lineal
σ


Rentabilidad vs. riesgo

Avg. Annual Rate
of Return Avg. Risk Premium
Portfolio Nominal Real (Extra vs. T.Bills)
Performance
histórica
Treasury Bills 3.9 0.8 0
de distintas
Goverment Bonds 5.7 2.7 1.8
Inversiones
Corporate Bonds 6.0 3.0 2.1
Common stocks (S&P 500) 13.0 9.7 9.1
(1926-2000)
Small-firm common stocks 17.3 13.8 13.4

Source: Ibbotson Associates, Inc., 2001 Yearbook


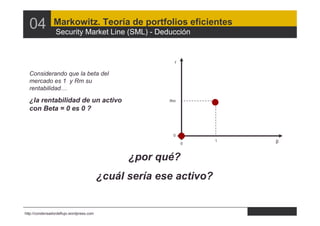
Security Market Line (SML) - Deducción

r

Considerando que la beta del
mercado es 1 y Rm su
rentabilidad…

¿la rentabilidad de un activo Rm

con Beta = 0 es 0 ?

0
1 β
0

¿por qué?
¿cuál sería ese activo?



r

Precisamente, estaríamos hablando
de los bonos del tesoro de EEUU

Ahora bien…
Rm

Rf

0
1 β
0

¿cómo hacemos para saber la relación
entre las betas del resto de los activos?



William Sharpe
¡En Wikipedia
hasta tengo foto!
(los otros… nada)

John Lintner the paper describing CAPM to the Journal ofJack in
Sharpe submitted Finance Treynor
1962. However, ironically, the paper, which would become one of the
foundations of financial economics was initially considered irrelevant and
rejected from publication.

Sharpe had to wait for the editorial staff to change until finally getting the paper
published in 1964. At the same time, the CAPM was independently
developed by John Lintner and Jack Treynor.



CAPM SML

Re- Rf = (Rm - Rf) β r

La prima de riesgo de un activo es la prima de riesgo
histórica del mercado y depende linealmente de la
variabilidad histórica de dicho activo frente al mercado.

Re = (Rm - Rf) β + Rf
)
El retorno esperado de un activo es como mínimo el retorno – Rf
(R m
de un activo libre de riesgo y puede ser mayor o menor que
la prima de mercado dependiendo de la variabilidad del
activo frente al mercado
Y = ax + b
El retorno esperado depende de la variabilidad histórica del
activo frente al mercado β

•¿Dónde ubicaría un activo de igual riesgo-retorno al de mercado en
? la SML? ¿Qué beta tendrá?
•¿Dónde ubicaría un activo sub-valuado? ¿Y uno sobre-valuado?



Highlights SML

r
a. Tasa libre de riesgo (Rf)
b. Tasa de rendimiento del mercado (Rm) E

c. Activo C con relación riesgo-retorno adecuada y por )
– Rf
ende con cotización eficiente. (R m
C
d. Activo D sin relación riesgo-retorno adecuada y por B
ende con cotización ineficiente.
e. Activo E sin relación riesgo-retorno adecuada y por A D
ende con cotización ineficiente

1 β

•¿El activo D se encuentra sobre o sub valuado?
•¿Y el activo E?
? •¿Puede subisistir dicha condición en el tiempo?
•¿Mediante que proceso se corregiría? Describirlo.


CAPM
04 Riesgo sistemático vs. No sistemático

Las inversiones diversificadas con eficiencia
Assumptions σ
pueden eliminar la mayoría del riesgo
no sistemático

• Inversores tienen mismo horizonte temporal
Riesgo no
sistemático
• Las inversiones se limitan a activos financieros
con cotización – Ej. Bonos, Acciones. Riesgo total

• No hay costos de transacción ni impuestos

• Inversores racionales – portafolios eficientes
(expectativas homogéneas) Riesgo sistemático

• Inversores analizan posibilidades de inversión con el mismo
criterio económico (expectativas sobre rentabilidad futura
de los activos) Q de títulos

• Inversores tienen aversión al riesgo

• Inversores pueden invertir y tomar prestado a Rf En equilibrio de mercado, se espera
que un activo brinde un rendimiento adecuado
a su riesgo inevitable
(riesgo que no puede diversificarse)


Business Risks – Enterprise Risk Management

MARKET RISKS BUSINESS RISKS
•Tipo de cambio •Economicos
•Tasas de interés •Reputación
•Equity Prices •Supply Chain
•Precios commodities •Tecnológicos
•Etc •Legales y regulatorios
•Medio ambiente
•Etc

Enterprise
Risks

OPERATIONAL RIESGO
RISKS CREDITICIO
•RRHH •Créditos por cobrar
•Procesos •Financiamiento de
•Sistemas proveedores
•Procedimientos •Cash Management
•Políticas
•etc


Manejo de incertidumbre con escenarios

Hoy hay que
Es necesario
decidir Hay una realidad Ninguna
proyectar
para responder Futura pero proyección
el futuro
a una realidad Infinitas será como la
para poder
futura proyecciones realidad
decidir hoy
incierta

Ninguna decisión
será perfecta

Una decisión
puede sentenciar
al fracaso
o al triunfo


Proceso de modelización de escenarios

Construcción Construccíón Determinación
Definición Elección de Construcción Análisis
de relación de escenario de variables
de variables Key drivers de escenarios resultados
de variables base sensibles

1 2 3 4 5 6 7

1. ¿Qué variables son las que generan el output (VAN, TIR, EBITDA) del modelo?
2. ¿Cómo se relacionan entre si las variables? El Excel sólo permite relaciones lineales o iteraciones mediante
macros. De necesitarse relaciones complejas y/o dinámicas se debe recurrir a herramientas específicas
3. Determinar los valores básicos de inicio para el modelo mediante research y criterio.
4. Análisis de Sensibilidad: En forma individiual por cada variable investigar la variación porcencual qie existe
en el output frente a la variación porcentual del input.
5. Elegir las variables que son sensibles y críticas para el output. No deben ser ni menos de tres ni más de 7 u
8.
6. Imaginar escenarios futuros con el correspondiente impacto que tendrán en cada una de las variables
sensibles. Consejo: trabajar con variaciones porcentuales sobre los valores del escenario base y no con
valores absolutos. (Ej: en un escenario de boom turistico los precios serán un 20% por encima del esceanrio
base)
7. Cargar en el modelo cada uno de los escenarios y ver las variaciones del output. La clave de la simulación
exitosa es la iteración.


Nociones genéricas - TIPS

40% Color azul para todas los valores
inputs
469.682 Color negro para los valores con fórmulas
Cuando se trabaja con proyecciones,
marcar en fondo gris el año base

Guardar al menos los valores del
1,50x escenario base
Cuando se arma un modelo con
proyecciones, cada hoja debe tener en la
misma columna los mismos años
Delimitar claramente con bordes y
negritas los subtotales y totales
267.273 Siempre poner puntos para separar cifras

4.586K De ser posible, trabajar con números con
65,30M pocas cifras y siempre formatearlos para
indicar la cuantía. (K=miles; M=millones;
1,25x x=veces; cualquier magnitud que sea
3,33ARS/USD necesaria


Riesgo 1C2010

Más contenido relacionado

Riesgo 1C2010