Unidad6
- 1. 6 Ecuaciones de primer y segundo grado Podemos encontrar en el día a día muchas situaciones donde se utilicen ecuaciones de primer y segundo grado. Por ejemplo, calcular el espacio que recorre un vehículo. INTERNET LECTURA INICIAL ESQUEMA ACTIVIDAD
- 2. Epitafio de Diofanto Busca en la web Enlace a la historia de Diofanto de Alejandría Enlace para resolver el epitafio Diofanto de Alejandría planteó un problema de ecuaciones de primer grado en su epitafio. ¿Te atreves a resolverlo?
- 3. Esquema de contenidos Ecuaciones de primer y segundo grado Ecuación de primer grado Identidad y ecuación Elementos Soluciones de una ecuación Resolución de ecuaciones de primer grado Ecuaciones sencillas Ecuaciones con paréntesis Ecuaciones con denominador Resolución de problemas con ecuaciones de primer grado Ecuaciones de 2º grado Concepto Resolución caso 1 Resolución caso 2 Resolución caso 3
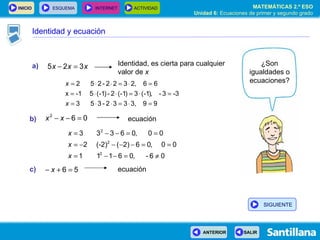
- 4. Una igualdad algebraica está formada por dos expresiones algebraicas separadas por un signo igual ( = ). Una igualdad algebraica es: Una identidad cuando es cierta para cualquier valor de las letras. Una ecuación si sólo es cierto para algunos valores de las letras. Identidad y ecuación SIGUIENTE
- 5. ¿Son igualdades o ecuaciones? a) b) c) Identidad y ecuación SIGUIENTE
- 6. ¿Son igualdades o ecuaciones? a) b) c) Identidad, es cierta para cualquier valor de x Identidad y ecuación SIGUIENTE
- 7. ¿Son igualdades o ecuaciones? a) b) c) Identidad, es cierta para cualquier valor de x Identidad y ecuación SIGUIENTE
- 8. ¿Son igualdades o ecuaciones? a) b) c) Identidad, es cierta para cualquier valor de x ecuación Identidad y ecuación SIGUIENTE
- 9. ¿Son igualdades o ecuaciones? a) b) c) Identidad, es cierta para cualquier valor de x ecuación Identidad y ecuación SIGUIENTE
- 10. ¿Son igualdades o ecuaciones? a) b) c) Identidad, es cierta para cualquier valor de x ecuación ecuación Identidad y ecuación SIGUIENTE
- 11. ¿Son igualdades o ecuaciones? a) b) c) Identidad, es cierta para cualquier valor de x ecuación ecuación Identidad y ecuación
- 12. Elementos de una ecuación de primer grado Miembro : en una ecuación hay dos expresiones separadas por un signo igual. La expresión situada a la izquierda es el primer miembro y la expresión de la derecha es el segundo miembro. Término : es cada uno de los sumandos de los miembros. Término independiente : es el miembro formado por un solo número. Incógnitas : son las letras cuyos valores desconocemos. Grado : Es el mayor de los exponentes con los que figura la incógnita. Incógnita x Grado 2
- 13. Soluciones Soluciones . Son los valores de la incógnita que hacen que la igualdad sea cierta. SIGUIENTE
- 14. Soluciones Soluciones . Son los valores de la incógnita que hacen que la igualdad sea cierta. Resolver una ecuación es encontrar su solución o sus soluciones. SIGUIENTE
- 15. Soluciones Soluciones . Son los valores de la incógnita que hacen que la igualdad sea cierta. Resolver una ecuación es encontrar su solución o sus soluciones. Dos ecuaciones son equivalentes cuando tienen las mismas soluciones. SIGUIENTE
- 16. Soluciones Soluciones . Son los valores de la incógnita que hacen que la igualdad sea cierta. Resolver una ecuación es encontrar su solución o sus soluciones. Dos ecuaciones son equivalentes cuando tienen las mismas soluciones. SUMAR + RESTAR - Si a los dos miembros de una ecuación se les suma o les resta el mismo número se obtiene otra ecuación equivalente. SIGUIENTE
- 17. Soluciones Soluciones . Son los valores de la incógnita que hacen que la igualdad sea cierta. Resolver una ecuación es encontrar su solución o sus soluciones. Dos ecuaciones son equivalentes cuando tienen las mismas soluciones. Si a los dos miembros de una ecuación se les suma o les resta el mismo número se obtiene otra ecuación equivalente. Si a los dos miembros de una ecuación se les multiplica o divide por el mismo número (distinto de cero) se obtiene otra ecuación equivalente. SUMAR + RESTAR - MULTIPLICAR X DIVIDIR :
- 18. Resolución de ecuaciones de primer grado Resolución de ecuaciones sencillas SIGUIENTE
- 19. Resolución de ecuaciones de primer grado Agrupamos los números en el 2º miembro Resolución de ecuaciones sencillas SIGUIENTE
- 20. Resolución de ecuaciones de primer grado Agrupamos los números en el 2º miembro Agrupamos las x en el 1 er miembro Resolución de ecuaciones sencillas SIGUIENTE
- 21. Resolución de ecuaciones de primer grado Agrupamos los números en el 2º miembro Agrupamos las x en el 1 er miembro Resolución de ecuaciones sencillas SIGUIENTE
- 22. Resolución de ecuaciones de primer grado Agrupamos los números en el 2º miembro Agrupamos las x en el 1 er miembro Operamos Agrupamos los términos en x en un miembro y los números en el otro. Resolución de ecuaciones sencillas SIGUIENTE
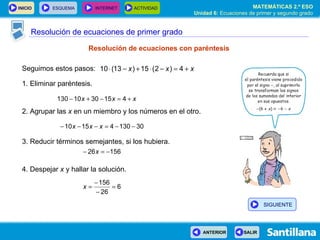
- 23. Resolución de ecuaciones de primer grado Seguimos estos pasos: 1. Eliminar paréntesis. 2. Agrupar las x en un miembro y los números en el otro. 3. Reducir términos semejantes, si los hubiera. 4. Despejar x y hallar la solución. Resolución de ecuaciones con paréntesis
- 24. Resolución de ecuaciones de primer grado Seguimos estos pasos: 1. Eliminar paréntesis. 2. Agrupar las x en un miembro y los números en el otro. 3. Reducir términos semejantes, si los hubiera. 4. Despejar x y hallar la solución. Resolución de ecuaciones con paréntesis SIGUIENTE
- 25. Resolución de ecuaciones de primer grado Seguimos estos pasos: 1. Eliminar paréntesis. 2. Agrupar las x en un miembro y los números en el otro. 3. Reducir términos semejantes, si los hubiera. 4. Despejar x y hallar la solución. Resolución de ecuaciones con paréntesis SIGUIENTE
- 26. Resolución de ecuaciones de primer grado Seguimos estos pasos: 1. Eliminar paréntesis. 2. Agrupar las x en un miembro y los números en el otro. 3. Reducir términos semejantes, si los hubiera. 4. Despejar x y hallar la solución. Resolución de ecuaciones con paréntesis SIGUIENTE
- 27. Resolución de ecuaciones de primer grado Seguimos estos pasos: 1. Eliminar paréntesis. 2. Agrupar las x en un miembro y los números en el otro. 3. Reducir términos semejantes, si los hubiera. 4. Despejar x y hallar la solución. Resolución de ecuaciones con paréntesis SIGUIENTE
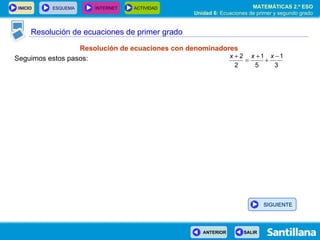
- 28. Resolución de ecuaciones de primer grado Seguimos estos pasos: Resolución de ecuaciones con denominadores SIGUIENTE
- 29. Resolución de ecuaciones de primer grado Seguimos estos pasos: 1. Eliminar denominadores. Resolución de ecuaciones con denominadores SIGUIENTE
- 30. Resolución de ecuaciones de primer grado Seguimos estos pasos: 1. Eliminar denominadores. Resolución de ecuaciones con denominadores SIGUIENTE
- 31. Resolución de ecuaciones de primer grado Seguimos estos pasos: 1. Eliminar denominadores. Resolución de ecuaciones con denominadores SIGUIENTE
- 32. Resolución de ecuaciones de primer grado Seguimos estos pasos: 1. Eliminar denominadores. Resolución de ecuaciones con denominadores 2. Eliminar paréntesis. SIGUIENTE
- 33. Resolución de ecuaciones de primer grado Seguimos estos pasos: 1. Eliminar denominadores. Resolución de ecuaciones con denominadores 2. Eliminar paréntesis. SIGUIENTE
- 34. Resolución de ecuaciones de primer grado Seguimos estos pasos: 1. Eliminar denominadores. 3. Agrupar las x en un miembro y los números en el otro. Resolución de ecuaciones con denominadores 2. Eliminar paréntesis. SIGUIENTE
- 35. Resolución de ecuaciones de primer grado Seguimos estos pasos: 1. Eliminar denominadores. 3. Agrupar las x en un miembro y los números en el otro. Resolución de ecuaciones con denominadores 2. Eliminar paréntesis. SIGUIENTE
- 36. Resolución de ecuaciones de primer grado Seguimos estos pasos: 1. Eliminar denominadores. 3. Agrupar las x en un miembro y los números en el otro. 4. Reducir términos semejantes, si los hubiera. Resolución de ecuaciones con denominadores 2. Eliminar paréntesis. SIGUIENTE
- 37. Resolución de ecuaciones de primer grado Seguimos estos pasos: 1. Eliminar denominadores. 3. Agrupar las x en un miembro y los números en el otro. 4. Reducir términos semejantes, si los hubiera. Resolución de ecuaciones con denominadores 2. Eliminar paréntesis. SIGUIENTE
- 38. Resolución de ecuaciones de primer grado Seguimos estos pasos: 1. Eliminar denominadores. 3. Agrupar las x en un miembro y los números en el otro. 4. Reducir términos semejantes, si los hubiera. 5. Despejar x y hallar la solución. Resolución de ecuaciones con denominadores 2. Eliminar paréntesis. SIGUIENTE
- 39. Resolución de ecuaciones de primer grado Seguimos estos pasos: 1. Eliminar denominadores. 3. Agrupar las x en un miembro y los números en el otro. 4. Reducir términos semejantes, si los hubiera. 5. Despejar x y hallar la solución. Resolución de ecuaciones con denominadores 2. Eliminar paréntesis.
- 40. Resolución de problemas con ecuaciones de primer grado Para resolver problemas mediante ecuaciones seguimos estos pasos: 1. Leer atentamente el enunciado e identificar la incógnita. 2. Plantear la ecuación. 3. Resolver la ecuación. 4. Comprobar que la solución es válida e interpretarla. SIGUIENTE
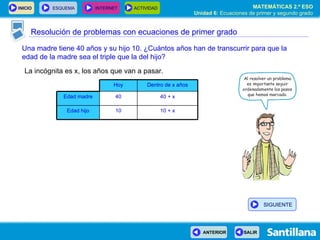
- 41. Resolución de problemas con ecuaciones de primer grado Una madre tiene 40 años y su hijo 10. ¿Cuántos años han de transcurrir para que la edad de la madre sea el triple que la del hijo? SIGUIENTE
- 42. Resolución de problemas con ecuaciones de primer grado La incógnita es x, los años que van a pasar. Una madre tiene 40 años y su hijo 10. ¿Cuántos años han de transcurrir para que la edad de la madre sea el triple que la del hijo? SIGUIENTE
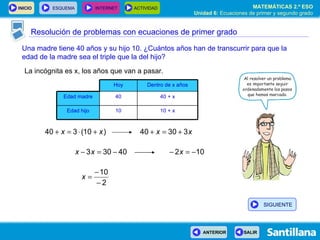
- 43. Resolución de problemas con ecuaciones de primer grado La incógnita es x, los años que van a pasar. Una madre tiene 40 años y su hijo 10. ¿Cuántos años han de transcurrir para que la edad de la madre sea el triple que la del hijo? 40 + x 40 Edad madre 10 + x 10 Edad hijo Dentro de x años Hoy SIGUIENTE
- 44. Resolución de problemas con ecuaciones de primer grado La incógnita es x, los años que van a pasar. Una madre tiene 40 años y su hijo 10. ¿Cuántos años han de transcurrir para que la edad de la madre sea el triple que la del hijo? 40 + x 40 Edad madre 10 + x 10 Edad hijo Dentro de x años Hoy SIGUIENTE
- 45. Resolución de problemas con ecuaciones de primer grado La incógnita es x, los años que van a pasar. Una madre tiene 40 años y su hijo 10. ¿Cuántos años han de transcurrir para que la edad de la madre sea el triple que la del hijo? 40 + x 40 Edad madre 10 + x 10 Edad hijo Dentro de x años Hoy SIGUIENTE
- 46. Resolución de problemas con ecuaciones de primer grado La incógnita es x, los años que van a pasar. Una madre tiene 40 años y su hijo 10. ¿Cuántos años han de transcurrir para que la edad de la madre sea el triple que la del hijo? 40 + x 40 Edad madre 10 + x 10 Edad hijo Dentro de x años Hoy SIGUIENTE
- 47. Resolución de problemas con ecuaciones de primer grado La incógnita es x, los años que van a pasar. Una madre tiene 40 años y su hijo 10. ¿Cuántos años han de transcurrir para que la edad de la madre sea el triple que la del hijo? 40 + x 40 Edad madre 10 + x 10 Edad hijo Dentro de x años Hoy SIGUIENTE
- 48. Resolución de problemas con ecuaciones de primer grado La incógnita es x, los años que van a pasar. Una madre tiene 40 años y su hijo 10. ¿Cuántos años han de transcurrir para que la edad de la madre sea el triple que la del hijo? 40 + x 40 Edad madre 10 + x 10 Edad hijo Dentro de x años Hoy SIGUIENTE
- 49. Resolución de problemas con ecuaciones de primer grado La incógnita es x, los años que van a pasar. Una madre tiene 40 años y su hijo 10. ¿Cuántos años han de transcurrir para que la edad de la madre sea el triple que la del hijo? 40 + x 40 Edad madre 10 + x 10 Edad hijo Dentro de x años Hoy SIGUIENTE
- 50. Resolución de problemas con ecuaciones de primer grado La incógnita es x, los años que van a pasar. Dentro de 5 años, la edad de la madre será 45 años y la edad del hijo será 15 años. Una madre tiene 40 años y su hijo 10. ¿Cuántos años han de transcurrir para que la edad de la madre sea el triple que la del hijo? 40 + x 40 Edad madre 10 + x 10 Edad hijo Dentro de x años Hoy
- 51. Ecuaciones de segundo grado Una ecuación de segundo grado con una incógnita es una igualdad algebraica con las siguientes características: Tiene una única incógnita. Alguno de sus términos es de grado 2 y no contiene términos de grado mayor que 2. a, b y c son números conocidos y SIGUIENTE
- 52. Ecuaciones de segundo grado Una ecuación de segundo grado con una incógnita es una igualdad algebraica con las siguientes características: Tiene una única incógnita. Alguno de sus términos es de grado 2 y no contiene términos de grado mayor que 2. a, b y c son números conocidos y Ecuación Coeficientes SIGUIENTE
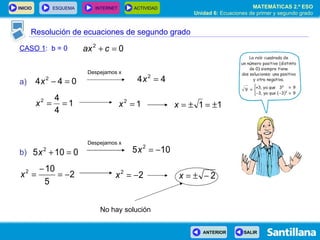
- 53. Resolución de ecuaciones de segundo grado CASO 1 : b = 0 SIGUIENTE
- 54. Resolución de ecuaciones de segundo grado CASO 1 : b = 0 a) Despejamos x SIGUIENTE
- 55. Resolución de ecuaciones de segundo grado CASO 1 : b = 0 a) Despejamos x b) Despejamos x No hay solución
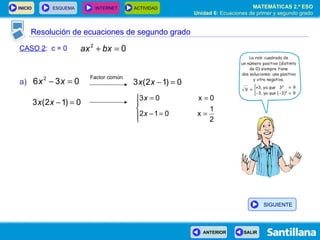
- 56. Resolución de ecuaciones de segundo grado CASO 2 : c = 0 SIGUIENTE
- 57. Resolución de ecuaciones de segundo grado CASO 2 : c = 0 a) Factor común SIGUIENTE
- 58. Resolución de ecuaciones de segundo grado CASO 2 : c = 0 a) Factor común b) Factor común
- 59. Resolución de ecuaciones de segundo grado CASO 3 : a) Las soluciones son x = -2 y x = -3. SIGUIENTE
- 60. Resolución de ecuaciones de segundo grado CASO 3 : b) La solución es doble: x = 3. SIGUIENTE
- 61. Resolución de ecuaciones de segundo grado CASO 3 : c) No existe ninguna solución.
- 62. Enlaces de interés La ciencia es divertida IR A ESTA WEB Problemas curiosos IR A ESTA WEB
- 63. Actividad: Buscando el error Dirección: http://www.santillana.cl/matematica/escenas/unidad2f.htm En la sección chilena de la Editorial Santillana, esta actividad se refiere a las ecuaciones de primer grado y la búsqueda de errores en su resolución. Para desarrollarla, sigue este enlace .