Unidade 1

1 Los números naturales Los números naturales resuelven con sencillez problemas de identificación o enumeración, como cuando identificamos con ellos a los corredores de una carrera. INTERNET LECTURA INICIAL ESQUEMA ACTIVIDAD

Srinivasa Ramanujan Busca en la web Enlace a una biografía de Ramanujan Enlace a la historia de la matemática india INICIO ESQUEMA INTERNET ACTIVIDAD

Esquema de contenidos Números naturales Definición Orden Operaciones Multiplicación División Potencias de números naturales Base y exponente de una potencia Producto de potencias de la misma base Cociente de potencias de la misma base Potencia de una potencia Potencia de una multiplicación Potencia de una división Raíces cuadradas Definición Raíces exacta y entera Aproximaciones y errores Definición Truncamiento Redondeo Error de la aproximación Operaciones combinadas Jerarquía de las operaciones

La propiedad distributiva interviene en muchos cálculos de la vida cotidiana sin que nos percatemos de ello. SIGUIENTE Propiedad distributiva de la multiplicación de los números naturales

La propiedad distributiva interviene en muchos cálculos de la vida cotidiana sin que nos percatemos de ello. Por ejemplo, supongamos que un camarero cobra 12 € por cada hora que trabaje en una cafetería durante una semana en las fiestas de un pueblo y que ha trabajado las siguientes horas en una semana. Su sueldo completo puede hallarse de dos maneras: - Calculando las cantidades que cobra cada día y sumándolas. - Sumando todas las horas trabajadas y multiplicando ese resultado por el sueldo horario. Haz tú los cálculos. SIGUIENTE 6 8 7 4 5 5 3 Horas Domingo Sábado Viernes Jueves Miércoles Martes Lunes Propiedad distributiva de la multiplicación de los números naturales

La propiedad distributiva interviene en muchos cálculos de la vida cotidiana sin que nos percatemos de ello. Por ejemplo, supongamos que un camarero cobra 12 € por cada hora que trabaje en una cafetería durante una semana en las fiestas de un pueblo y que ha trabajado las siguientes horas en una semana. Su sueldo completo puede hallarse de dos maneras: - Calculando las cantidades que cobra cada día y sumándolas: - Sumando todas las horas trabajadas y multiplicando ese resultado por el sueldo horario: 3 · 12 + 5 · 12 + 5 · 12 + 4 · 12 + 7·12 +8·12 + 6 · 12 = 36 + 60 + 60 + 48 + 84 + 96 + 72 = 456 € SIGUIENTE 6 8 7 4 5 5 3 Horas Domingo Sábado Viernes Jueves Miércoles Martes Lunes Propiedad distributiva de la multiplicación de los números naturales

La propiedad distributiva interviene en muchos cálculos de la vida cotidiana sin que nos percatemos de ello. Por ejemplo, supongamos que un camarero cobra 12 € por cada hora que trabaje en una cafetería durante una semana en las fiestas de un pueblo y que ha trabajado las siguientes horas en una semana. Su sueldo completo puede hallarse de dos maneras: - Calculando las cantidades que cobra cada día y sumándolas: - Sumando todas las horas trabajadas y multiplicando ese resultado por el sueldo horario: 3 · 12 + 5 · 12 + 5 · 12 + 4 · 12 + 7 · 12 +8 · 12 + 6 · 12 = 36 + 60 + 60 + 48 + 84 + 96 + 72 = 456 € (3 + 5 + 5 + 4 + 7 + 8 + 6) · 12 = 38 · 12 = 456 € Como ves, de las dos maneras da el mismo resultado. 6 8 7 4 5 5 3 Horas Domingo Sábado Viernes Jueves Miércoles Martes Lunes Propiedad distributiva de la multiplicación de los números naturales

División de números naturales Dividir es repartir una cantidad en partes iguales. La cantidad repartida se llama dividendo . Al número de partes iguales se le llama divisor . Cada parte obtenida se llama cociente . Si no sobra nada, la división es exacta . Si queda algo sin repartir se dice que la división es no exacta o entera, y a esa cantidad sobrante se le llama resto , que es siempre menor que el divisor. SIGUIENTE

Dividir es repartir una cantidad en partes iguales. La cantidad repartida se llama dividendo . Al número de partes iguales se le llama divisor . Cada parte obtenida se llama cociente . Si no sobra nada, la división es exacta . Si queda algo sin repartir, se dice que la división es no exacta o entera , y a esa cantidad sobrante se le llama resto , que es siempre menor que el divisor. He hecho una división que me dio de resto 10. El divisor y el cociente eran 9 y 12, pero no sé cuál es cuál. Ayúdame. División de números naturales SIGUIENTE

Dividir es repartir una cantidad en partes iguales. La cantidad repartida se llama dividendo . Al número de partes iguales se le llama divisor . Cada parte obtenida se llama cociente . Si no sobra nada, la división es exacta . Si queda algo sin repartir se dice que la división es no exacta o entera , y a esa cantidad sobrante se le llama resto , que es siempre menor que el divisor. He hecho una división que me dio de resto 10. El divisor y el cociente eran 9 y 12, pero no sé cuál es cuál. Ayúdame. Independientemente del valor del dividendo, puesto que el resto, 10, ha de ser menor que el divisor, éste ha de ser 12 y el cociente, por tanto, 9. Así que el dividendo es 12 · 9 + 10, o sea, 118. División de números naturales SIGUIENTE

Dividir es repartir una cantidad en partes iguales. La cantidad repartida se llama dividendo . Al número de partes iguales se le llama divisor . Cada parte obtenida se llama cociente . Si no sobra nada, la división es exacta . Si queda algo sin repartir, se dice que la división es no exacta o entera , y a esa cantidad sobrante se le llama resto , que es siempre menor que el divisor. Ayúdame de nuevo. He hecho cuatro divisiones y se me han mezclado todos los datos. Tengo como dividendos, divisores, cocientes y restos los números: 0, 3, 4, 5, 7, 8, 10, 11, 13, 35, 41 y 62. Dime qué divisiones hice. División de números naturales SIGUIENTE

Dividir es repartir una cantidad en partes iguales. La cantidad repartida se llama dividendo . Al número de partes iguales se le llama divisor . Cada parte obtenida se llama cociente . Si no sobra nada, la división es exacta . Si queda algo sin repartir, se dice que la división es no exacta o entera , y a esa cantidad sobrante se le llama resto , que es siempre menor que el divisor. Ayúdame de nuevo. He hecho tres divisiones y se me han mezclado todos los datos. Tengo como dividendos, divisores, cocientes y restos los números: 0, 3, 4, 5, 7, 8, 10, 11, 13, 35, 41 y 62. Dime qué divisiones hice. Los tres dividendos han de ser los tres números mayores, 35, 41 y 62, pues si no, tendríamos que tener a 1 como cociente. División de números naturales SIGUIENTE

Dividir es repartir una cantidad en partes iguales. La cantidad repartida se llama dividendo . Al número de partes iguales se le llama divisor . Cada parte obtenida se llama cociente . Si no sobra nada, la división es exacta . Si queda algo sin repartir, se dice que la división es no exacta o entera , y a esa cantidad sobrante se le llama resto , que es siempre menor que el divisor. Ayúdame de nuevo. He hecho tres divisiones y se me han mezclado todos los datos. Tengo como dividendos, divisores, cocientes y restos los números: 0, 3, 4, 5, 7, 8, 10, 11, 13, 35, 41 y 62. Dime qué divisiones hice. Los tres dividendos han de ser los tres números mayores, 35, 41 y 62, pues si no, tendríamos que tener a 1 como cociente. Hay un resto 0 y la división exacta posible es 35 entre 5 o 7. Quedan, pues, 3, 4, 8, 10, 11, 13, 41 y 62. Prueba 41 con los posibles divisores 3, 4, 8, 10 u 11. División de números naturales SIGUIENTE

Dividir es repartir una cantidad en partes iguales. La cantidad repartida se llama dividendo . Al número de partes iguales se le llama divisor . Cada parte obtenida se llama cociente . Si no sobra nada, la división es exacta . Si queda algo sin repartir, se dice que la división es no exacta o entera , y a esa cantidad sobrante se le llama resto , que es siempre menor que el divisor. Ayúdame de nuevo. He hecho tres divisiones y se me han mezclado todos los datos. Tengo como dividendos, divisores, cocientes y restos los números: 0, 3, 4, 5, 7, 8, 10, 11, 13, 35, 41 y 62. Dime qué divisiones hice. Los tres dividendos han de ser los tres números mayores, 35, 41 y 62, pues si no, tendríamos que tener a 1 como cociente. Hay un resto 0 y la división exacta posible es 35 entre 5 o 7. Quedan, pues, 3, 4, 8, 10, 11, 13, 41 y 62. Prueba 41 con los posibles divisores 3, 4, 8, 10 u 11. Habrás obtenido ya que las divisiones posibles son: o División de números naturales 7 0 5 35 5 0 7 35 3 8 11 41 4 10 13 62

Potencia de una multiplicación y de una división Tú conoces las dos propiedades de la p otencia de una multiplicación y de una división : ¡No te confundas! Si en vez de productos o cocientes ponemos sumas o restas, esta propiedad no es cierta: y y no es lo mismo que no es lo mismo que SIGUIENTE

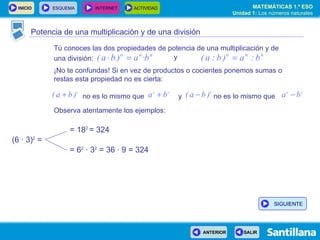
Potencia de una multiplicación y de una división Tú conoces las dos propiedades de p otencia de una multiplicación y de una división : ¡No te confundas! Si en vez de productos o cocientes ponemos sumas o restas esta propiedad no es cierta: y Observa atentamente los ejemplos: (6 · 3) 2 = = 18 2 = 324 = 6 2 · 3 2 = 36 · 9 = 324 y no es lo mismo que no es lo mismo que SIGUIENTE

Potencia de una multiplicación y de una división Tú conoces las dos propiedades de p otencia de una multiplicación y de una división : ¡No te confundas! Si en vez de productos o cocientes ponemos sumas o restas, esta propiedad no es cierta: y Observa atentamente los ejemplos: (6 · 3) 2 = = 18 2 = 324 = 6 2 · 3 2 = 36 · 9 = 324 (6 : 3) 2 = = 2 2 = 4 = 6 2 : 3 2 = 36 : 9 = 4 y no es lo mismo que no es lo mismo que SIGUIENTE

Potencia de una multiplicación y de una división Tú conoces las dos propiedades de p otencia de una multiplicación y de una división : ¡No te confundas! Si en vez de productos o cocientes ponemos sumas o restas esta propiedad no es cierta: y Observa atentamente los ejemplos: (6 · 3) 2 = = 18 2 = 324 = 6 2 · 3 2 = 36 · 9 = 324 (6 : 3) 2 = = 2 2 = 4 = 6 2 : 3 2 = 36 : 9 = 4 (6 + 3) 2 = = 9 2 = 81 = 6 2 + 3 2 = 36 + 9 = 45 y no es lo mismo que no es lo mismo que SIGUIENTE

Potencia de una multiplicación y de una división Tú conoces las dos propiedades de p otencia de una multiplicación y de una división : ¡No te confundas! Si en vez de productos o cocientes ponemos sumas o restas, esta propiedad no es cierta: y Observa atentamente los ejemplos: (6 · 3) 2 = = 18 2 = 324 = 6 2 · 3 2 = 36 · 9 = 324 (6 : 3) 2 = = 2 2 = 4 = 6 2 : 3 2 = 36 : 9 = 4 (6 + 3) 2 = = 9 2 = 81 (6 - 3) 2 = = 3 2 = 9 = 6 2 - 3 2 = 36 - 9 = 27 y no es lo mismo que no es lo mismo que = 6 2 + 3 2 = 36 + 9 = 45

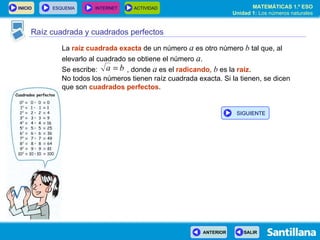
Raíz cuadrada y cuadrados perfectos La raíz cuadrada exacta de un número a es otro número b tal que, al elevarlo al cuadrado se obtiene el número a . Se escribe: , donde a es el radicando , b es la raíz . No todos los números tienen raíz cuadrada exacta. Si la tienen, se dicen que son cuadrados perfectos . SIGUIENTE

Raíz cuadrada y cuadrados perfectos No todos los números tienen raíz cuadrada exacta. Si la tienen, se dice que son cuadrados perfectos . Es curioso que si vamos sumando los números impares 1, 3, 5,... , aparecen los cuadrados perfectos. SIGUIENTE

Raíz cuadrada y cuadrados perfectos Es curioso que si vamos sumando los números impares, 1, 3, 5,... , aparecen los cuadrados perfectos. No todos los números tienen raíz cuadrada exacta. Si la tienen, se dice que son cuadrados perfectos . 1 = 1 = 1 2 SIGUIENTE

Raíz cuadrada y cuadrados perfectos Es curioso que si vamos sumando los números impares 1, 3, 5,... , aparecen los cuadrados perfectos. No todos los números tienen raíz cuadrada exacta. Si la tienen, se dice que son cuadrados perfectos . 1 = 1 = 1 2 1 + 3 = 4 = 2 2 SIGUIENTE

Raíz cuadrada y cuadrados perfectos Es curioso que si vamos sumando los números impares 1, 3, 5,... , aparecen los cuadrados perfectos. No todos los números tienen raíz cuadrada exacta. Si la tienen, se dice que son cuadrados perfectos . 1 = 1 = 1 2 1 + 3 = 4 = 2 2 1 + 3 + 5 = 9 = 3 2 SIGUIENTE

Raíz cuadrada y cuadrados perfectos Es curioso que si vamos sumando los números impares 1, 3, 5,... , aparecen los cuadrados perfectos. No todos los números tienen raíz cuadrada exacta. Si la tienen, se dice que son cuadrados perfectos . 1 = 1 = 1 2 1 + 3 = 4 = 2 2 1 + 3 + 5 = 9 = 3 2 1 + 3 + 5 + 7 = 16 = 4 2 SIGUIENTE

Raíz cuadrada y cuadrados perfectos Es curioso que si vamos sumando los números impares 1, 3, 5,... , aparecen los cuadrados perfectos. 1 = 1 = 1 2 1 + 3 = 4 = 2 2 1 + 3 + 5 = 9 = 3 2 1 + 3 + 5 + 7 = 16 = 4 2 1 + 3 + 5 + 7 + 9 = 25 = 5 2 No todos los números tienen raíz cuadrada exacta. Si la tienen, se dice que son cuadrados perfectos . Y así, sucesivamente.

Jerarquía de las operaciones En una expresión pueden aparecer diversas operaciones combinadas . Para hallar el valor de la misma, se ha de seguir estrictamente el siguiente orden en su cálculo: 1.º Las operaciones que estén incluidas entre paréntesis . 2.º Las potencias y las raíces . 3.º Los productos y las divisiones , de izquierda a derecha. 4.º Las sumas y las restas , de izquierda a derecha. SIGUIENTE

Jerarquía de las operaciones En una expresión pueden aparecer diversas operaciones combinadas . Para hallar el valor de la misma, se ha de seguir estrictamente el siguiente orden en su cálculo: 1.º Las operaciones que estén incluidas entre paréntesis . 2.º Las potencias y las raíces . 3.º Los productos y las divisiones , de izquierda a derecha. 4.º Las sumas y las restas , de izquierda a derecha. Aplícalo a un caso concreto: 56 + 4 · 3 2 – (2 3 + 17 ) : 5 SIGUIENTE

Jerarquía de las operaciones En una expresión pueden aparecer diversas operaciones combinadas . Para hallar el valor de la misma, se ha de seguir estrictamente el siguiente orden en su cálculo: 1.º Las operaciones que estén incluidas entre paréntesis . 2.º Las potencias y las raíces . 3.º Los productos y las divisiones , de izquierda a derecha. 4.º Las sumas y las restas , de izquierda a derecha. Aplícalo a un caso concreto: 56 + 4 · 3 2 – (2 3 + 17 ) : 5 56 + 4 · 3 2 – ( 8 + 17) : 5 SIGUIENTE

Jerarquía de las operaciones En una expresión pueden aparecer diversas operaciones combinadas . Para hallar el valor de la misma, se ha de seguir estrictamente el siguiente orden en su cálculo: 1.º Las operaciones que estén incluidas entre paréntesis . 2.º Las potencias y las raíces . 3.º Los productos y las divisiones , de izquierda a derecha. 4.º Las sumas y las restas , de izquierda a derecha. Aplícalo a un caso concreto: 56 + 4 · 3 2 – (2 3 + 17 ) : 5 56 + 4 · 3 2 – ( 8 + 17) : 5 56 + 4 · 3 2 – 25 : 5 SIGUIENTE

Jerarquía de las operaciones En una expresión pueden aparecer diversas operaciones combinadas . Para hallar el valor de la misma, se ha de seguir estrictamente el siguiente orden en su cálculo: 1.º Las operaciones que estén incluidas entre paréntesis . 2.º Las potencias y las raíces . 3.º Los productos y las divisiones , de izquierda a derecha. 4.º Las sumas y las restas , de izquierda a derecha. Aplícalo a un caso concreto: 56 + 4 · 3 2 – (2 3 + 17 ) : 5 56 + 4 · 3 2 – ( 8 + 17) : 5 56 + 4 · 3 2 – 25 : 5 56+ 4 · 9 – 25 : 5 SIGUIENTE

Jerarquía de las operaciones En una expresión pueden aparecer diversas operaciones combinadas . Para hallar el valor de la misma, se ha de seguir estrictamente el siguiente orden en su cálculo: 1.º Las operaciones que estén incluidas entre paréntesis . 2.º Las potencias y las raíces . 3.º Los productos y las divisiones , de izquierda a derecha. 4.º Las sumas y las restas , de izquierda a derecha. Aplícalo a un caso concreto: 56 + 4 · 3 2 – (2 3 + 17 ) : 5 56 + 4 · 3 2 – ( 8 + 17) : 5 56 + 4 · 3 2 – 25 : 5 56 + 4 · 9 – 25 : 5 56 + 36 – 25 : 5 SIGUIENTE

Jerarquía de las operaciones En una expresión pueden aparecer diversas operaciones combinadas . Para hallar el valor de la misma, se ha de seguir estrictamente el siguiente orden en su cálculo: 1.º Las operaciones que estén incluidas entre paréntesis . 2.º Las potencias y las raíces . 3.º Los productos y las divisiones , de izquierda a derecha. 4.º Las sumas y las restas , de izquierda a derecha. Aplícalo a un caso concreto: 56 + 4 · 3 2 – (2 3 + 17 ) : 5 56 + 4 · 3 2 – ( 8 + 17) : 5 56 + 4 · 3 2 – 25 : 5 56 + 4 · 9 – 25 : 5 56 + 36 – 25 : 5 56 + 36 – 5 SIGUIENTE

Jerarquía de las operaciones En una expresión pueden aparecer diversas operaciones combinadas . Para hallar el valor de la misma, se ha de seguir estrictamente el siguiente orden en su cálculo: 1.º Las operaciones que estén incluidas entre paréntesis . 2.º Las potencias y las raíces . 3.º Los productos y las divisiones , de izquierda a derecha. 4.º Las sumas y las restas , de izquierda a derecha. Aplícalo a un caso concreto: 56 + 4 · 3 2 – (2 3 + 17 ) : 5 56 + 4 · 3 2 – ( 8 + 17) : 5 56 + 4 · 3 2 – 25 : 5 56 + 4 · 9 – 25 : 5 56 + 36 – 25 : 5 56 + 36 – 5 92 – 5 SIGUIENTE

Jerarquía de las operaciones En una expresión pueden aparecer diversas operaciones combinadas . Para hallar el valor de la misma, se ha de seguir estrictamente el siguiente orden en su cálculo: 1.º Las operaciones que estén incluidas entre paréntesis . 2.º Las potencias y las raíces . 3.º Los productos y las divisiones , de izquierda a derecha. 4.º Las sumas y las restas , de izquierda a derecha. Aplícalo a un caso concreto: 56 + 4 · 3 2 – (2 3 + 17 ) : 5 56 + 4 · 3 2 – ( 8 + 17) : 5 56 + 4 · 3 2 – 25 : 5 56 + 4 · 9 – 25 : 5 56 + 36 – 25 : 5 56 + 36 – 5 92 – 5 87

Enlaces de interés Diversidad en Matemáticas IR A ESTA WEB Retos Matemáticos IR A ESTA WEB

Actividad: Los números triangulares Dirección: http :// www.santillana.cl / matematica /escenas/unidad1aa. htm En la sección chilena de la editorial Santillana, esta actividad se refiere a la sucesión de los números triangulares, definidos ya en la matemática griega. Para desarrollarla, sigue este enlace . INICIO

Unidade 1

Más contenido relacionado

Unidade 1